
Обучение с подкреплением
В заключительной лекции нашего курса мы познакомимся с ещё одной парадигмой машинного обучения, обучением с подкреплением, которая в настоящее время крайне активно развивается и имеет свои приложения в различных предметных областях. Для удобства и непротиворечивости определения данной парадигмы рассмотрим сперва ключевые особенности уже известных нам подходов. В предыдущих лекциях мы с вами познакомились с такими парадигмами машинного обучения, как обучение с учителем (supervised learning) и обучение без учителя (unsupervised learning):
Обучение с учителем:
Типичный пример — решение задачи классификации рукописных цифр в датасете MNIST при помощи CNN.
Обучение без учителя:
Типичный пример — использование метода k-средних для решения задачи кластеризации.
Легко заметить, что ключевой особенностью этих ML-парадигм является работа с датасетом как с исчерпывающей и не изменяющейся сущностью. По сути, именно набор данных и определяет решаемую в этих подходах задачу.

Легко придумать постановку задачи, в которой невозможно составить такой исчерпывающий датасет. Например, разрабатывая автопилот для автомобиля, мы вряд ли сможем составить обучающую выборку, в которой будут перечислены все возможные дорожные ситуации в условиях плотного городского трафика, для которых к тому же будет известна разметка "ground true" целевой переменной о предпочтительном решении автопилота в них.
Невозможность собрать исчерпывающий датасет во многом может быть связана с тем, как в примере с автопилотом автомобиля, что результат работы алгоритма может существенно изменить состояние окружающей его среды, которая и является источником данных. При этом, не имея всей картины возможных действий и их последствий, мы можем предоставить нашему алгоритму возможность взаимодействовать с источником данных (средой) и постфактум оценить действия нашего алгоритма (агента), и, используя эту оценку, подстроить алгоритм так, чтобы он чаще совершал желательные действия, и реже — нежелательные. В литературе такую оценку называют вознаграждением (reward). В этом случае обучение строится таким образом, чтобы алгоритм (агент) стремился максимизировать получаемое вознаграждение.
Функция вознаграждения (reward) в этом случае является аналогом функции потерь из парадигмы обучения с учителем, но имеет ряд отличий:
Для вычисления функции потерь в парадигме обучения с учителем нам было достаточно одного ответа модели для сравнения с целевой переменной. В свою очередь, reward может быть связан с конкретной последовательностью предсказаний алгоритма (решений). Например: получению очков за победу в шахматной партии соответствует выбор целой последовательности правильных ходов игрока; безаварийная поездка беспилотного автомобиля между двумя точками на карте раскладывается на огромное количество решений о замедлении, ускорении и поворотах.
Весь используемый нами ранее аппарат обучения с учителем основывался на том, что при помощи градиентных методов мы подбирали такие веса модели машинного обучения, чтобы дифференцируемая loss-функция имела при них локальный минимум. Некоторые постановки задач, такие как рассмотренные ранее задачи построения автопилота или написание играющего в шахматы алгоритма, не допускают возможности составить дифференцируемую функцию награды. Убирая требование дифференцируемости reward-функции, мы лишаемся возможности применить известные нам алгоритмы оптимизации, такие как стохастический градиентный спуск и его улучшения.
Если у нас есть набор примеров с правильными ответами, то мы используем эту выборку для обучения нашей модели, а после обучения применяем её к неразмеченным данным. Именно этот подход мы использовали, когда обучали классификатор для MNIST, подавая на вход сети картинки с изображениями рукописных цифр и считая градиент для подстройки весов на основе разницы между известным лэйблом цифры и выходом нейросети.
Таким образом, мы можем резюмировать особенности парадигмы обучения с подкреплением.
Обучение с подкрплением:
Типичные примеры — оптимизация дискретных функционалов, задачи оптимального управления, RLHF.
Достаточную интуицию о парадигме обучения с подкреплением и об области решаемых с её помощью задач можно сформировать, если поставить знак равенства между терминами "обучение с подкреплением" и "обучение методом проб и ошибок".

[arxiv] 🎓 Deep Reinforcement Learning for Autonomous Driving: A Survey
[arxiv] 🎓 Reinforcement Learning and Control as Probabilistic Inference: Tutorial and Review
[git] 🐾 Lecture notes and exercises for control theory course
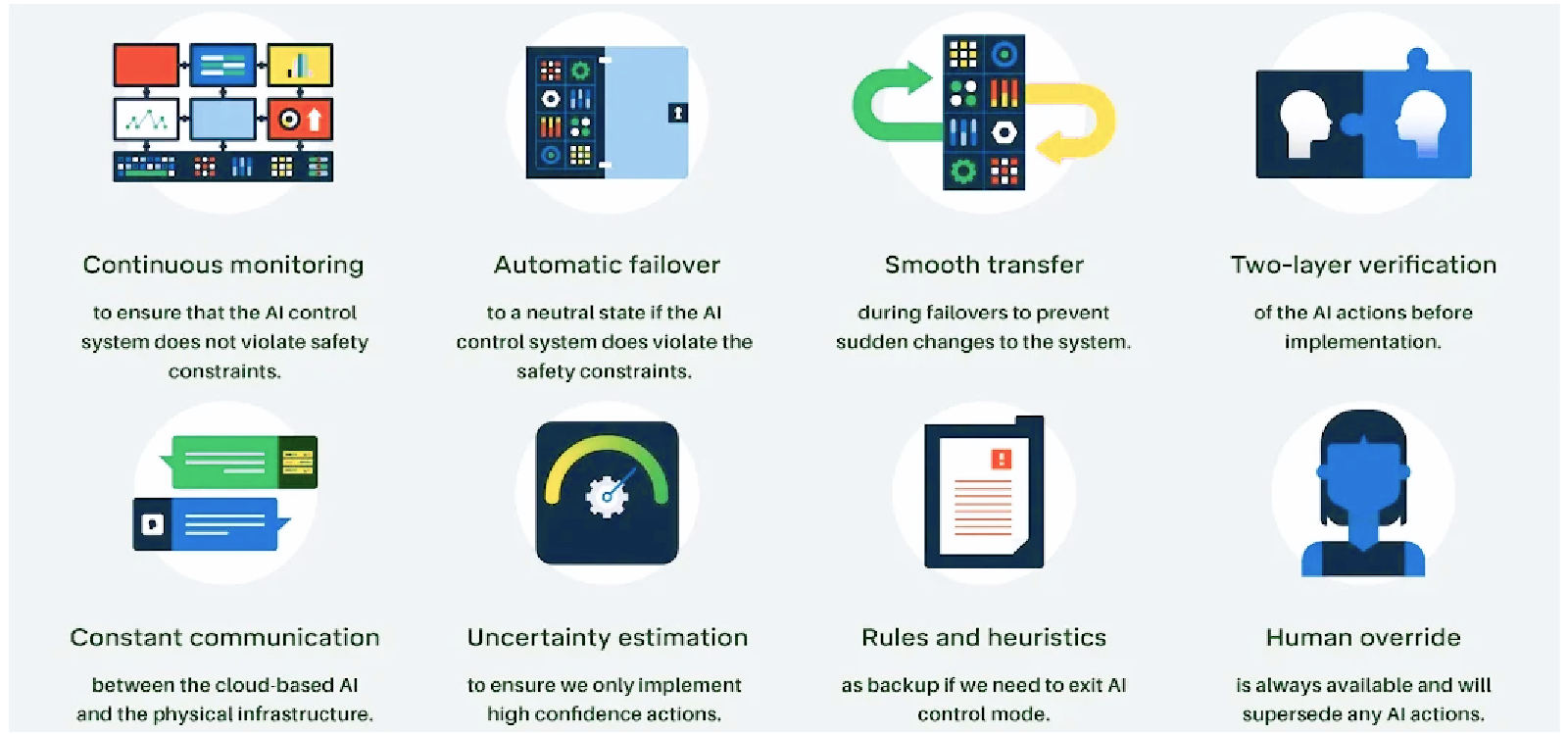
В настоящее время большое число исследовательских групп занято разработкой решений для создания беспилотного транспорта. Алгоритм принятия решений в таких решениях часто основан на алгоритмах обучения с подкреплением (Deep reinforcement learning on-board an autonomous car ✏️[blog]):
from IPython.display import HTML
from base64 import b64encode
# Source: https://wayve.ai/wp-content/uploads/2022/06/ezgif.com-gif-maker1.mp4
!wget -qN https://edunet.kea.su/repo/EduNet-web_dependencies/dev-2.0/L15/rl_control_system.mp4
mp4 = open("rl_control_system.mp4", "rb").read()
data_url = f"data:video/mp4;base64,{b64encode(mp4).decode()}"
HTML(f"<video width=1000 controls><source src={data_url} type='video/mp4'></video>")
[article] 🎓 Reinforcement learning for combinatorial optimization: A survey
[arxiv] 🎓 Neural Combinatorial Optimization with Reinforcement Learning
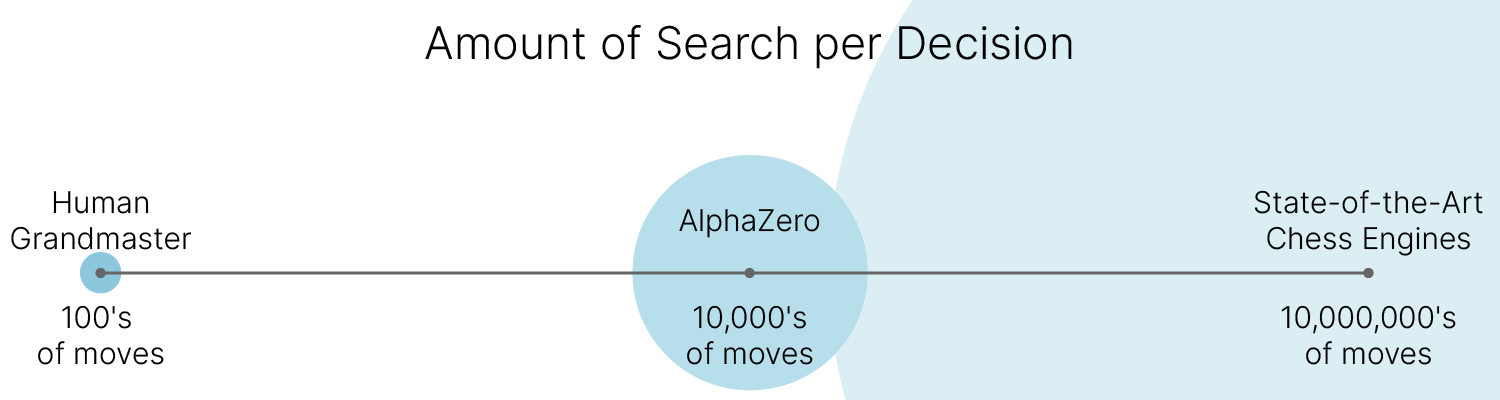
[book] 📚 Reinforcement Learning for NLP
[arxiv] 🎓 Training language models to follow instructions with human feedback
Прочие приложения:
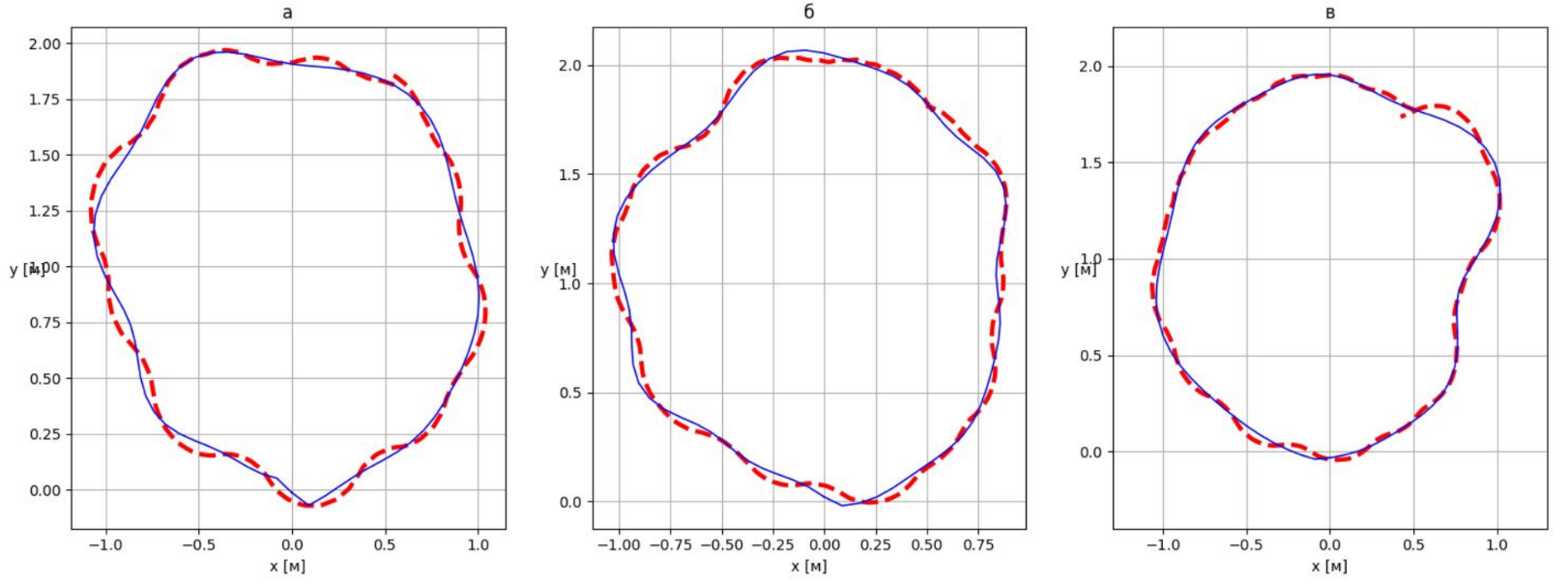
В работе Управление движением сферического робота с помощью нейронной сети решалась задача подбора управляющего сигнала для робота, позволяющего ему двигаться по определенной заранее траектории на плоскости.
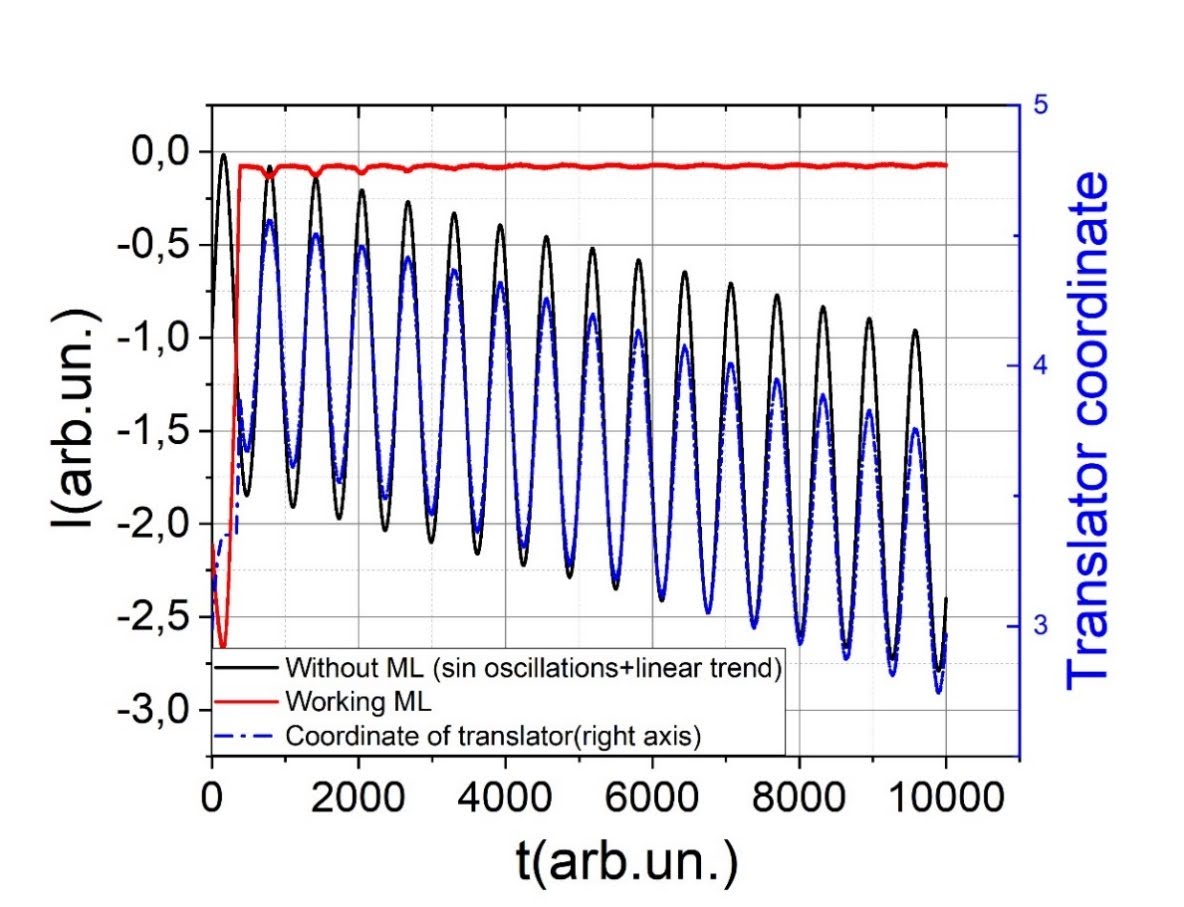
В работе Самоюстирующиеся оптические системы на основе машинного обучения с подкреплением был разработан управляющий алгоритм, позволяющий автоматизировать и ускорить процесс настройки сложной оптической экспериментальной установки.

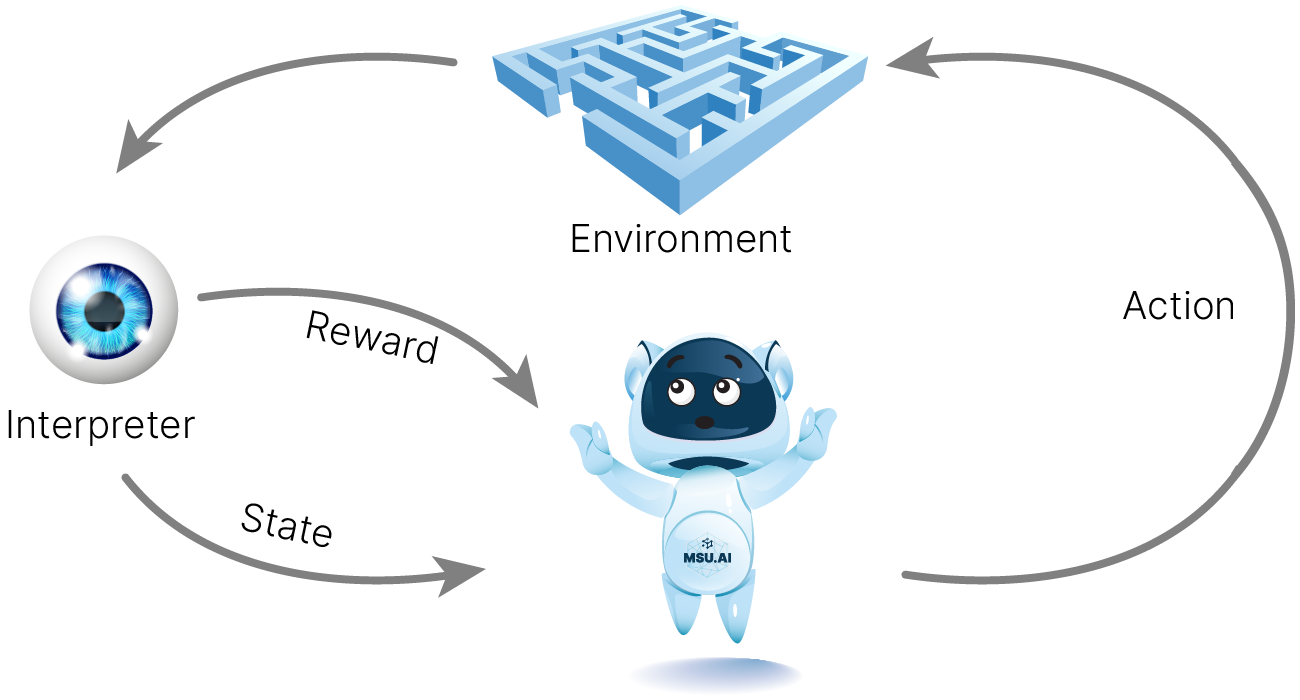
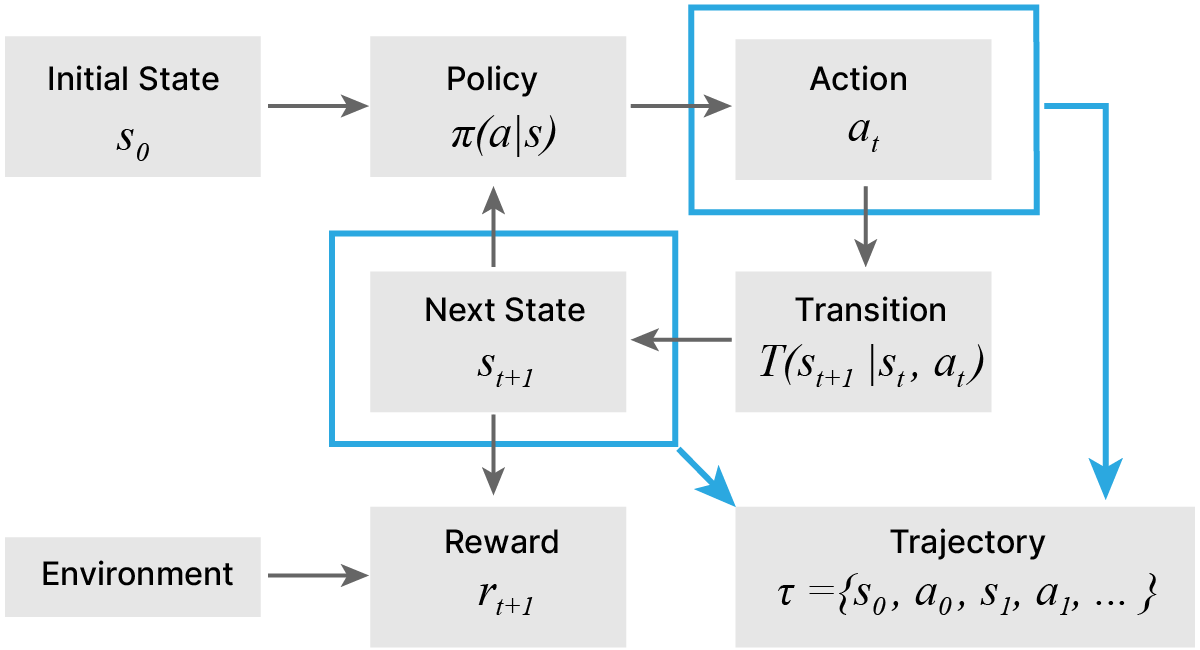
Агент и среда — ключевые понятия в обучении с подкреплением.
Агент — программа, принимающая решение о дальнейших действиях на основе информации о состоянии среды.
Среда — это всё, с чем агент может прямо или косвенно взаимодействовать. Среда обладает состоянием (State). Агент может влиять на среду, совершая какие-то действия (Actions), переводя среду при этом из одного состояния в другое и получая какое-то вознаграждение. Среда описывается пространством возможных состояний. Конкретное состояние — вектор в этом пространстве.
В зависимости от конкретной задачи агент может наблюдать либо полное состояние среды, либо только некоторую его часть. Во втором случае агенту может потребоваться какое-то внутреннее представление полного состояния, которое будет обновляться по мере получения новых данных.
Функция награды (reward) — вводимая программистом формула вычисления ценности действия на основе финального результата, ожидания этого результата, промежуточных результатов и любых других параметров, которые будут подсказывать путь к наилучшей последовательности действий агента. Это некоторый аналог функции потерь, без которой непонятно, чему учиться. Например, в шахматах истинная награда — это победа, но взятая фигура соперника тоже ценна и должна увеличивать награду, если мы хотим подсказать агенту, что брать чужие фигуры полезно. Может ли после этого агент получить мат, позарившись на незащищенную фигуру? Да, ровно как и неопытный шахматный игрок.
Попытка передать через дополнительные неосновные награды подсказки к получению основной награды называется reward shaping.
Эпизод — серия взаимодействий агента со средой (например, партия в игре).
Рассмотрим простейший пример среды для задачи обучения с подкреплением:
Фактически можно сказать, что такая среда всегда находится в одном состоянии или вообще не имеет состояния. Для нас будет важно, что выдаваемый средой reward не обязан быть дифференцируемым, и потому работа агента по взаимодействию с такой вырожденной средой не может быть корректно решена в рамках парадигмы обучения с учителем.
Примером stateless-среды может послужить классическая задача о многоруких бандитах 📚[wiki].

Согласно условиям данной задачи мы имеем:
Задача: игроку необходимо придумать такую стратегию нажатия на рычаги многорукого бандита, которая бы обеспечивала максимум возможного выигрыша.
Для того, чтобы приступить к решению этой задачи, нам необходимо создать модель описанной среды. Воспользуемся библиотекой Gymnasium, которую часто используют при решении задач методами обучения с подкреплением.
Перед тем, как приступить к созданию интересующей нас среды, разберемся, что такое Gymnasium и какие возможности он предоставляет для обучения с подкреплением.
Gymnasium (Gym) — это набор инструментов для разработки и сравнения алгоритмов RL, позволяющий стандартизировать взаимодействие между разными алгоритмами RL и средами. Также он предоставляет набор стандартных сред, которые могут, в том числе, использоваться для бенчмаркинга.
Для начала рассмотрим устройство среды Gym в целом. Среда — это некоторая модель мира, отвечающая за предоставление наблюдений и вознаграждений, в которой существует агент. Состояние среды будет изменяться в зависимости от действий агента.
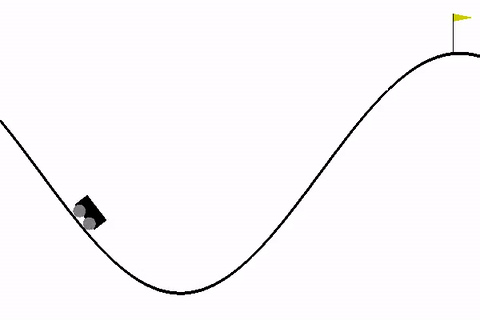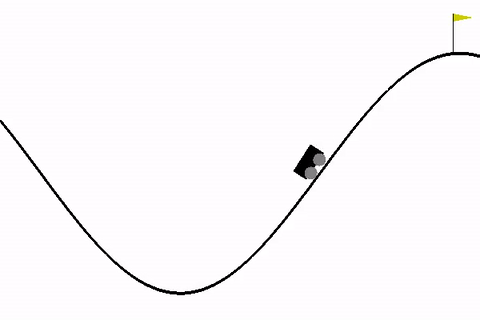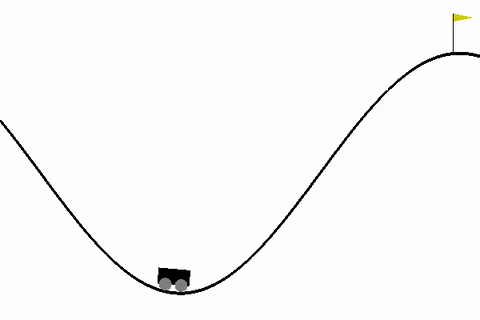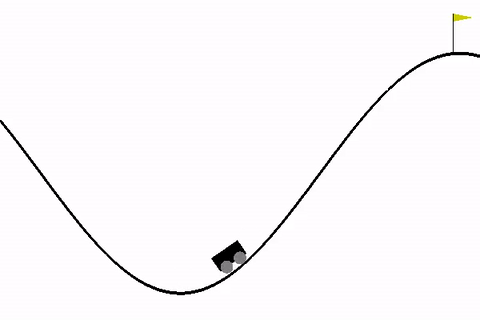
Рассмотрим для начала стандартную среду MountainCar, в которой стоит задача — довести машину до вершины горы.
!pip install -q gymnasium
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 953.9/953.9 kB 8.6 MB/s eta 0:00:00
import gym as openaigym
import gymnasium as gym
env = gym.make("MountainCar-v0")
В Gym среды представлены классом gym.Env, который является унифицированным интерфейсом среды со следующими атрибутами и методами:
action_space: описание действий, допустимых в данной среде;observation_space: структура и допустимые значения наблюдений состояния среды;reset(): сбрасывает среду и возвращает случайное исходное состояние;step(action): метод, продвигающий развитие окружающей среды на одно действие и возвращающий информацию о результате этого действия, а именно:Также в классе gym.Env есть несколько вспомогательных методов, например, render(), позволяющий представить наблюдение в понятной человеку форме, но мы не будем их касаться в нашей лекции.
Действия агента могут быть дискретными, непрерывными и комбинированными. Дискретные действия представлены фиксированным набором и взаимно исключают друг друга, например, нажатие/отпускание клавиши. Непрерывным действиям соответствуют значения в некотором диапазоне, например, поворот руля от -720 до 720 градусов. В среде мы не ограничены каким-то одним действием, и вполне допустимо одновременное нажатие нескольких кнопок и одновременный поворот руля. Аналогичным образом наблюдения могут быть дискретными (лампочка включена/выключена) или непрерывными (тензоры, соответствующие цветным изображениям).
Давайте посмотрим на то, как выглядят пространства действий и наблюдений в среде MountainCar:
from IPython.display import clear_output
# Action and observation space
action_space = env.action_space
obs_space = env.observation_space
clear_output()
print(f"The action space: {action_space}")
print(f"The observation space: {obs_space}")
The action space: Discrete(3) The observation space: Box([-1.2 -0.07], [0.6 0.07], (2,), float32)
Мы видим, что пространство наблюдений и действий представлено некоторыми классами Box и Discrete соответственно. Что же это за классы? Для объединения нескольких пространств действий (например, непрерывных и дискретных) в одно действие, в Gym существует специальный класс контейнеров.
Discrete представляет набор $n$ взаимоисключающих элементов. Например, Discrete(n=4) может быть использован для пространства действий с 4 направлениями движения ($\leftarrow \downarrow \rightarrow \uparrow$).Box представляет n-мерный тензор рациональных чисел в некотором диапазоне [low, high]. Например, нажатие педали газа от минимального значения 0 до максимального — 1, можно закодировать как с, аналогично наблюдение экрана игры, можно закодировать как Box(low=0, high=255, shape=(100, 50, 3), dtype=np.float32).Давайте посмотрим на диапазон допустимых значений пространства наблюдений в среде MountainCar:
print("Upper Bound for Env Observation", env.observation_space.high)
print("Lower Bound for Env Observation", env.observation_space.low)
Upper Bound for Env Observation [0.6 0.07] Lower Bound for Env Observation [-1.2 -0.07]
Обе структуры данных происходят от класса gym.Space
print(type(env.action_space))
print(type(env.observation_space))
<class 'gymnasium.spaces.discrete.Discrete'> <class 'gymnasium.spaces.box.Box'>
Также стоит упомянуть еще один дочерний класс gym.Space — Tuple, позволяющий объединять несколько экземпляров класса gym.Space вместе. Благодаря этому классу мы можем создавать пространства действий и наблюдений любой сложности.
В классе gym.Space реализованы методы, позволяющие взаимодействовать с пространствами действий и наблюдений:
sample(): возвращает случайный пример из пространства наблюдений,contains(x): проверяет принадлежность аргумента к пространству наблюдений.Давайте возьмем случайное действие, доступное нам в исходном состоянии среды MountainCar:
random_action = env.action_space.sample() # random number from 0 to 2
print(random_action)
1
Давайте попробуем совершить случайное действие, которое мы выбрали выше, для этого перезапустим среду, чтобы вернуться в изначальное состояние, и сделаем шаг с помощью метода step():
# Reset the environment and see the initial observation
obs, info = env.reset()
print(f"The initial observation is {obs}")
# Take the action and get the new observation space
new_obs, reward, done, truncated, info = env.step(random_action)
print(f"The new observation is {new_obs}")
The initial observation is [-0.57499045 0. ] The new observation is [-5.7460654e-01 3.8391253e-04]
Одна из простых задач обучения с подкреплением — задача о многоруких бандитах. В этой задаче состояние среды не меняется, а у агента есть фиксированный набор действий, которые он может выполнять.
Эту задачу можно представить таким образом: вы игрок в казино с игровыми автоматами, в которых с различной вероятностью возможно выиграть приз различной величины. Ваша задача как агента — выиграть как можно больше денег, бросая монетки в автоматы на ваш выбор.
Допустим, в казино находятся 4 автомата, лишь для одного из которых средний выигрыш будет > 1.
Давайте напишем класс, который будет описывать эту ситуацию.
import random
import numpy as np
from gym import Env, spaces
np.random.seed(42)
class MultiArmedBanditEnv(Env):
def __init__(self, n=4):
"""
n - number of arms in the bandit
"""
self.num_bandits = n
self.action_space = spaces.Discrete(self.num_bandits)
self.observation_space = spaces.Discrete(1) # the reward of the last action
self.bandit_success_prob = np.array(
[0.5, 0.1, 0.9, 0.2]
) # success probabilities
self.bandit_reward = np.array([2, 20, 1, 3])
def step(self, action):
done = True
result_prob = np.random.random()
if result_prob < self.bandit_success_prob[action]:
reward = self.bandit_reward[action]
else:
reward = 0
return reward, done
В нашем казино для того, чтобы принять участие в игре, нужно заплатить 1 монету. После оплаты игрок может нажать на любой рычаг игрового автомата и получить выигрыш с соответствующей вероятностью.
Как именно в таком случае мы можем определить, за какой рычаг нам стоит дергать, чтобы максимизировать выигрыш? Ведь мы как игрок не знаем вероятности выигрыша для разных рычагов.
Попробуем сделать это жадным способом: на каждом шаге будем совершать действие, имеющее максимальную оценку, и, в зависимости от результата, будем обновлять эту оценку.
Давайте разберемся, что она представляет.
Оценить ценность того или иного действия можно по среднему выигрышу, к которому оно приведет.
Пусть $R_n$ — награда, полученная за выполнение $n$-го действия. Тогда оценкой ценности действия будет $\displaystyle Q_n=\frac{R_1+R_2+...+R_n}{n}$. Величина $Q_n$ по сути представляет собой простое скользящее среднее (simple moving average), которое может вычисляться постепенно:
$\displaystyle Q_n = \frac{1}{n}(R_n+(n-1)Q_{n-1}) = \frac{1}{n}(R_n+nQ_{n-1}-Q_{n-1}) = Q_{n-1}+\frac{1}{n}(R_n-Q_{n-1})$
В целом, подобная схема обновления параметров в обучении с подкреплением, представимая как новая оценка:=старая оценка + шаг[цель — старая оценка], встречается довольно часто и называется incremental update rule.
Для получения оценок действий жадным способом нам понадобится функция argmax, которая будет выбирать действие с наибольшей оценкой, а в случае равенства максимальной оценки будет выбирать случайное действие.
def argmax(x):
return np.random.choice(np.flatnonzero(x == x.max()))
class GreedyAgent:
def __init__(self):
"""
Our agent initializes reward estimates as zeros.
This estimates will be updated incrementally after each
interaction with the environment.
"""
self.reward_estimates = np.zeros(4)
self.action_count = np.zeros(4)
self.cache = 1000 # initial amount of coins agent posesses
def get_action(self):
# Pay 1 coin for the action
self.cache -= 1
# Select greedy action
action = argmax(self.reward_estimates)
# Add a 1 to action selected in the action count
self.action_count[action] += 1
return action
def update_estimates(self, reward, action):
# Update amount of cache by reward from our previuos action
self.cache += reward
# Compute the difference between the received rewards vs the reward estimates
error = reward - self.reward_estimates[action]
# Update the reward estimate incementally
n = self.action_count[action]
self.reward_estimates[action] += (1 / n) * error
import matplotlib.pyplot as plt
env = MultiArmedBanditEnv()
agent = GreedyAgent()
mean_reward_greedy = []
rewards = []
while (agent.cache > 0) and (len(mean_reward_greedy) != 10000):
act = agent.get_action()
reward, done = env.step(act)
agent.update_estimates(reward, act)
rewards.append(reward)
mean_reward_greedy.append(sum(rewards) / (len(rewards)))
print(f"Action counts: {agent.action_count}")
print(f"Reward estimates: {agent.reward_estimates}")
plt.plot(mean_reward_greedy)
plt.show()
Action counts: [ 0. 0. 10000. 0.] Reward estimates: [0. 0. 0.9051 0. ]
Видно, что жадная стратегия не позволяет нам добиться оптимального принятия решений, поскольку оптимальную стратегию легко пропустить, если в начале агенту не повезет.
Вместо жадной стратегии будем использовать $\varepsilon$-жадную стратегию, которую можно описать как "оптимизм при неопределенности". Суть $\varepsilon$-жадной стратегии заключается в следующем: с некоторой вероятностью $\varepsilon$ совершать случайное действие, а с вероятностью $1-\varepsilon$ вести себя жадно.
$\varepsilon$ — важный параметр алгоритма. Как правило, в начале используют большие значения $\varepsilon$, тогда агент действует почти случайно и "исследует мир", а затем их уменьшают, и действия агента становятся близкими к оптимальным.
Выбор величины $\varepsilon$ связан с так называемым exploration-exploitation trade-off. Он может быть легко проиллюстрирован примером, когда вы не можете решить, пойти ли сегодня в любимый ресторан или попробовать сходить в новый? Новый ресторан может оказаться лучшего привычного, но это решение связано с риском разочарования.

class EpsilonGreedyAgent(GreedyAgent):
def __init__(self, epsilon):
GreedyAgent.__init__(self)
# Store the epsilon value
assert epsilon >= 0 and epsilon <= 1
self.epsilon = epsilon
def get_action(self):
# We need to redefine this function so that it takes an exploratory action with epsilon probability
# Pay 1 coin for the action
self.cache -= 1
# One hot encoding: 0 if exploratory, 1 otherwise
action_type = int(np.random.random() > self.epsilon)
# Generate both types of actions for every experiment
exploratory_action = np.random.randint(4)
greedy_action = argmax(self.reward_estimates)
# Use the one hot encoding to mask the actions for each experiment
action = greedy_action * action_type + exploratory_action * (1 - action_type)
self.action_count[action] += 1
return action
agent = EpsilonGreedyAgent(epsilon=0.25)
mean_reward_e_greedy = []
rewards = []
while (agent.cache > 0) and (len(mean_reward_e_greedy) != 10000):
act = agent.get_action()
reward, done = env.step(act)
agent.update_estimates(reward, act)
rewards.append(reward)
mean_reward_e_greedy.append(sum(rewards) / len(rewards))
# Decrease epsilon with time until we reach 0.01 chanse to perform exploratory action
if agent.epsilon > 0.01:
agent.epsilon -= 0.0001
print(f"Action counts: {agent.action_count}")
print(f"Reward estimates: {agent.reward_estimates}")
plt.plot(mean_reward_greedy)
plt.plot(mean_reward_e_greedy)
plt.show()
Action counts: [ 91. 9683. 137. 89.] Reward estimates: [0.96703297 2.00970774 0.8540146 0.80898876]
Использование $\epsilon$-жадной стратегии позволило нам иногда совершать "разведывательные" решения, которые могли быть не оптимальны относительно буквальной интерпретации накопленного нами ранее опыта. Аналогичного эффекта мы бы могли достигнуть, если бы определили нашу стратегию принятия решения вероятностной.
Пусть мы находимся в состоянии $s$, для которого возможны $K$ действий $\{a_i\}$. Определим величину $\pi(a_i|s)$:
Данное распределение вероятности принято называть политикой (policy).
Для "игры" с использованием такой политики нам нужно:
from numpy.random import choice
from scipy.special import softmax
class SoftmaxAgent(GreedyAgent):
def __init__(self):
GreedyAgent.__init__(self)
def get_action(self):
# We need to redefine this function so that it takes an action with probability pi(a,s)
# Pay 1 coin for the action
self.cache -= 1
# get \pi(a_i|s):
pi = softmax(self.reward_estimates)
# sample action
action = choice(np.arange(0, 4, 1), 1, p=pi)[0]
self.action_count[action] += 1
return action
agent = SoftmaxAgent()
mean_reward_softmax_agent = []
rewards = []
while (agent.cache > 0) and (len(mean_reward_softmax_agent) != 10000):
act = agent.get_action()
reward, done = env.step(act)
agent.update_estimates(reward, act)
rewards.append(reward)
mean_reward_softmax_agent.append(sum(rewards) / len(rewards))
clear_output()
print(f"Action counts: {agent.action_count}")
print(f"Reward estimates: {agent.reward_estimates}")
plt.plot(mean_reward_greedy)
plt.plot(mean_reward_e_greedy)
plt.plot(mean_reward_softmax_agent)
plt.show()
Action counts: [1766. 5262. 1660. 1312.] Reward estimates: [0.99207248 2.05245154 0.89578313 0.59222561]
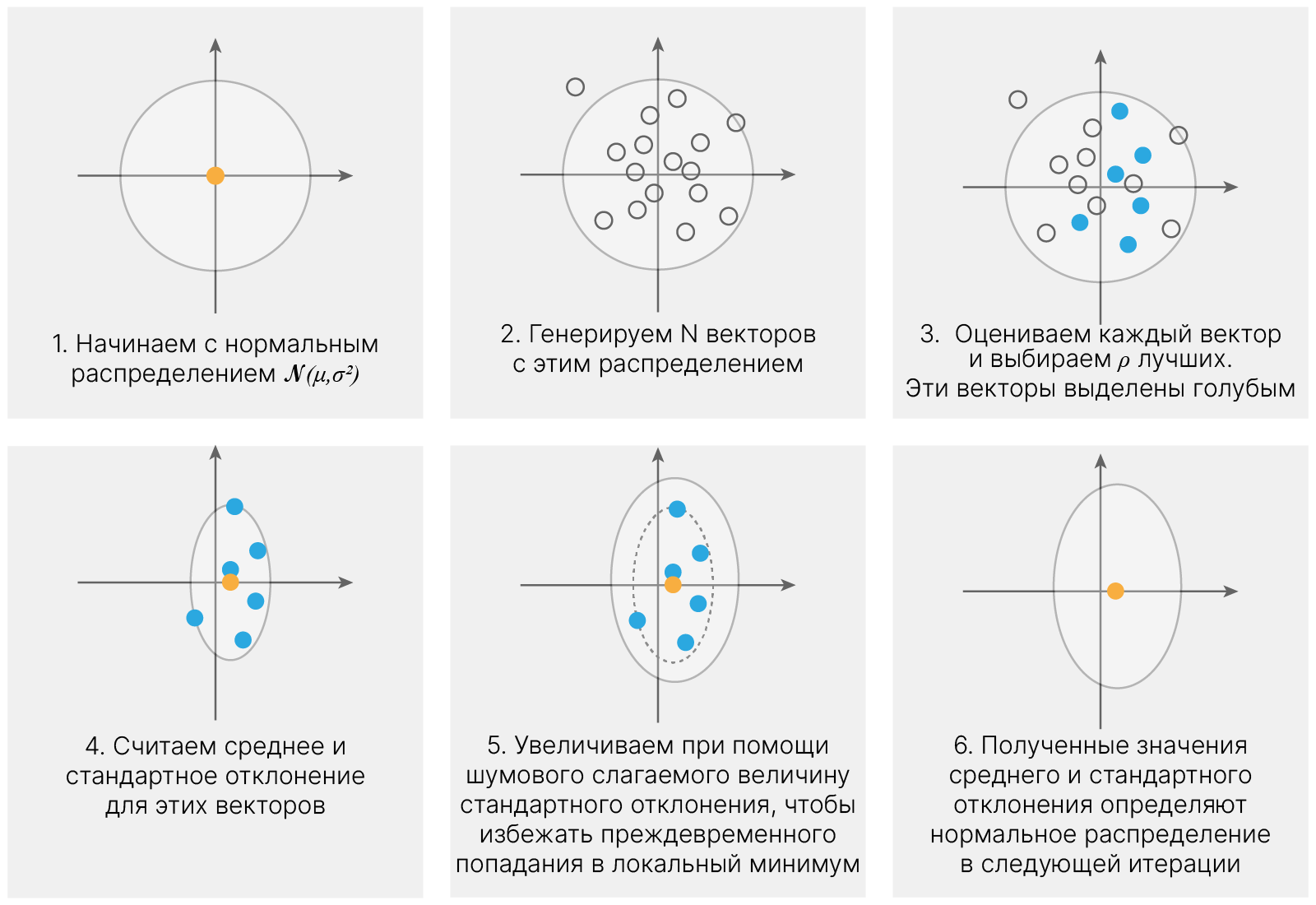
Одним из простейших алгоритмов нахождения оптимальной политики является Cross-entropy method (CEM). Он состоит из следующих простых этапов:
import torch
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
device
device(type='cuda', index=0)
Воспользуемся готовой средой MountainCarContinuous 🛠️[doc]:
import gym
from IPython.display import clear_output
env = gym.make("MountainCarContinuous-v0")
env.seed(42)
clear_output()
print("observation space:", env.observation_space)
print("action space:", env.action_space)
print(" - low:", env.action_space.low)
print(" - high:", env.action_space.high)
observation space: Box([-1.2 -0.07], [0.6 0.07], (2,), float32) action space: Box(-1.0, 1.0, (1,), float32) - low: [-1.] - high: [1.]
Создадим агента:
import math
import torch.nn as nn
import torch.nn.functional as F
class Agent(nn.Module):
def __init__(self, env, h_size=16):
super(Agent, self).__init__()
self.env = env
# state, hidden layer, action sizes
self.s_size = env.observation_space.shape[0]
self.h_size = h_size
self.a_size = env.action_space.shape[0]
# define layers (we used 2 layers)
self.fc1 = nn.Linear(self.s_size, self.h_size)
self.fc2 = nn.Linear(self.h_size, self.a_size)
def set_weights(self, weights):
s_size = self.s_size
h_size = self.h_size
a_size = self.a_size
# separate the weights for each layer
fc1_end = (s_size * h_size) + h_size
fc1_W = torch.from_numpy(weights[: s_size * h_size].reshape(s_size, h_size))
fc1_b = torch.from_numpy(weights[s_size * h_size : fc1_end])
fc2_W = torch.from_numpy(
weights[fc1_end : fc1_end + (h_size * a_size)].reshape(h_size, a_size)
)
fc2_b = torch.from_numpy(weights[fc1_end + (h_size * a_size) :])
# set the weights for each layer
self.fc1.weight.data.copy_(fc1_W.view_as(self.fc1.weight.data))
self.fc1.bias.data.copy_(fc1_b.view_as(self.fc1.bias.data))
self.fc2.weight.data.copy_(fc2_W.view_as(self.fc2.weight.data))
self.fc2.bias.data.copy_(fc2_b.view_as(self.fc2.bias.data))
def get_weights_dim(self):
return (self.s_size + 1) * self.h_size + (self.h_size + 1) * self.a_size
def forward(self, x):
x = F.relu(self.fc1(x))
x = torch.tanh(self.fc2(x))
return x.cpu().data
def act(self, state):
state = torch.from_numpy(state).float().to(device)
with torch.no_grad():
action = self.forward(state)
return action
def evaluate(self, weights, gamma=1.0, max_t=5000):
self.set_weights(weights)
episode_return = 0.0
state = self.env.reset()
for t in range(max_t):
state = torch.from_numpy(state).float().to(device)
action = self.forward(state)
state, reward, done, _ = self.env.step(action)
episode_return += reward * math.pow(gamma, t)
if done:
break
return episode_return
clear_output()
Реализуем Cross-Entropy Method:
import numpy as np
from collections import deque
from tqdm.notebook import tqdm
np.random.seed(42)
def cem(
agent,
n_iterations=5,
max_t=1000,
gamma=1.0,
print_every=10,
pop_size=50,
elite_frac=0.2,
sigma=0.5,
):
"""PyTorch implementation of the cross-entropy method.
Params
======
Agent (object): agent instance
n_iterations (int): maximum number of training iterations
max_t (int): maximum number of timesteps per episode
gamma (float): discount rate
print_every (int): how often to print average score (over last 100 episodes)
pop_size (int): size of population at each iteration
elite_frac (float): percentage of top performers to use in update
sigma (float): standard deviation of additive noise
"""
n_elite = int(pop_size * elite_frac)
scores_deque = deque(maxlen=100)
scores = []
# Initialize the weight with random noise
best_weight = sigma * np.random.randn(agent.get_weights_dim())
for i_iteration in tqdm(range(1, n_iterations + 1)):
# Define the cadidates and get the reward of each candidate
weights_pop = [
best_weight + (sigma * np.random.randn(agent.get_weights_dim()))
for i in range(pop_size)
]
rewards = np.array(
[agent.evaluate(weights, gamma, max_t) for weights in weights_pop]
)
# Select best candidates from collected rewards
elite_idxs = rewards.argsort()[-n_elite:]
elite_weights = [weights_pop[i] for i in elite_idxs]
best_weight = np.array(elite_weights).mean(axis=0)
reward = agent.evaluate(best_weight, gamma=1.0)
scores_deque.append(reward)
scores.append(reward)
torch.save(agent.state_dict(), "checkpoint.pth")
if i_iteration % print_every == 0:
print(
"Episode {}\tAverage Score: {:.2f}".format(
i_iteration, np.mean(scores_deque)
)
)
if np.mean(scores_deque) >= 90.0:
print(
"\nEnvironment solved in {:d} iterations!\tAverage Score: {:.2f}".format(
i_iteration - 100, np.mean(scores_deque)
)
)
break
return scores
np.bool8 = np.bool_
agent = Agent(env).to(device)
scores = cem(agent)
0%| | 0/5 [00:00<?, ?it/s]
import matplotlib.pyplot as plt
# Plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(1, len(scores) + 1), scores)
plt.ylabel("Score")
plt.xlabel("Episode #")
plt.show()
!mkdir -p video
import glob
import base64, io
from IPython import display
from IPython.display import HTML
from gym.wrappers.monitoring import video_recorder
def show_video(env_name):
mp4list = glob.glob("video/*.mp4")
if len(mp4list) > 0:
mp4 = "video/{}.mp4".format(env_name)
video = io.open(mp4, "r+b").read()
encoded = base64.b64encode(video)
display.display(
HTML(
data="""<video alt="test" autoplay
loop controls style="height: 400px;">
<source src="data:video/mp4;base64,{0}" type="video/mp4" />
</video>""".format(
encoded.decode("ascii")
)
)
)
else:
print("Could not find video")
def show_video_of_model(agent, env_name):
env = gym.make(env_name)
vid = video_recorder.VideoRecorder(env, path="video/{}.mp4".format(env_name))
agent.load_state_dict(torch.load("checkpoint.pth"))
state = env.reset()
done = False
while not done:
vid.capture_frame()
action = agent.act(state)
next_state, reward, done, _ = env.step(action)
state = next_state
if done:
break
env.close()
agent = Agent(env).to(device)
show_video_of_model(agent, "MountainCarContinuous-v0")
clear_output()
clear_output()
print("Необученная модель:")
show_video("MountainCarContinuous-v0")
Необученная модель:
Загрузим веса обученной в течение 500 эпизодов модели:
!wget -qN https://edunet.kea.su/repo/EduNet-content/dev-2.0/L15/weights/checkpoint.pth
agent = Agent(env).to(device)
show_video_of_model(agent, "MountainCarContinuous-v0")
clear_output()
clear_output()
print("Обученная модель:")
show_video("MountainCarContinuous-v0")
Обученная модель:
Итак, мы разобрались с самой простой ситуацией, многорукими бандитами, в которой среда постоянно находится в одном и том же состоянии. Однако в реальности чаще всего состояние среды, из которой агент делает новый ход, будет изменяться. Например, при игре в шахматы агент должен учитывать то, что после его хода и хода оппонента позиция на доске изменится.
Нам нужно определить некий процесс, в котором агент последовательно переходит из состояния в состояние в зависимости от своих действий, в некоторых состояниях получая награды.
Сделаем также важное предположение о природе нашего процесса: он полностью описывается своим текущим состоянием. Все, что произойдет в будущем, не зависит от информации из прошлого, кроме той, что мы уже наблюдаем в настоящем. Такой процесс называется марковским. Заметим, что описанный нами процесс в примере с многорукими бандитами также является марковским.
Приведем другие классические примеры марковского процесса:
Игральный кубик. Мы знаем, что на нем выпадет любая из граней с некоторой фиксированной вероятностью. На это никак не влияет то, что до этого на кубике выпало 6 шестерок подряд. Это может повлиять на нашу оценку вероятностей выпадения той или иной грани, но не на реальную вероятность.
Шахматы. "Текущая позиция на доске + чей ход" однозначно описывает игру.
А подходит ли покер?
С одной стороны, да. Текущее количество денег у каждого из игроков однозначно описывает игру. Но это если мы не учитываем блеф и другие факторы, которые могут сработать / не сработать в зависимости от предыдущих ситуаций в игре. То есть, все зависит от того, как именно мы будем описывать покер и какие допущения накладываем.
И получение хорошего представления S — тоже важная задача.
"The future is independent of the past given the present"
Состояние $S_{t}$ является Марковским тогда и только тогда, когда: $$ \large p\left(r_{t}, s_{t+1} \mid s_{0}, a_{0}, r_{0}, \ldots, s_{t}, a_{t}\right)=p\left(r_{t}, s_{t+1} \mid s_{t}, a_{t}\right) $$
Что происходит потом, зависит только от предыдущего состояния.
Вероятность перехода в новое состояние зависит только от текущего состояния и текущего действия.
Марковский процесс описывает полностью наблюдаемые (fully observable) среды. Можно описать их так:
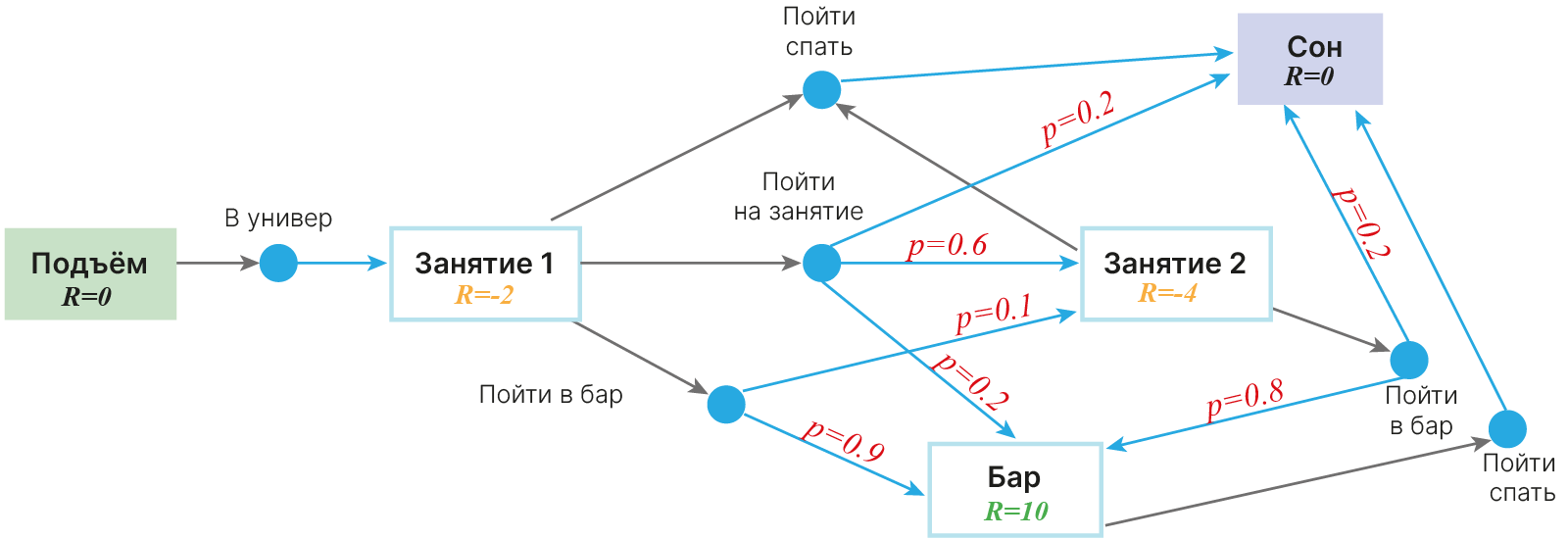
Представим себе, что студент живет вот по такой схеме. Заметим, что влиять в такой схеме на свои решения он не может: все решается подкидыванием кубика.

Марковский процесс (цепь) — это кортеж $(S, P)$, где
Строго говоря, необходимо еще распределение начальных состояний (но мы предполагаем, что оно вырождено, т.е. мы знаем, где начинаем, с вероятностью 1).
Марковский процесс — основа для RL. Мы будем постепенно усложнять эту модель, добавляя rewards и actions.
В определении нам встретилась матрица переходов, зададим ее тоже формально.
Markov decision process (MDP)
До этого у нас получалось не совсем адекватное представление процесса — студент не мог ни на что повлиять. На самом же деле студент может решать, куда ему надо: в аудиторию, домой спать или в бар. Однако наше действие не всегда определяет состояние, в которое мы перейдем.
Хочет наш студент пойти на лекцию, но по пути встречает товарища, и идут они в бар. Хочет он пойти спать, а по пути к выходу из университета встречает лектора с хорошей памятью и идет на лекцию. И т.д.
Как это отразить на схеме так, чтобы это можно было прочитать? Введем промежуточные состояния, куда нас переводят действия студента. А уже из этих промежуточных состояний случайно будем переходить в состояния среды.
MDP — это кортеж $(S, A, R, P, \gamma)$, где:
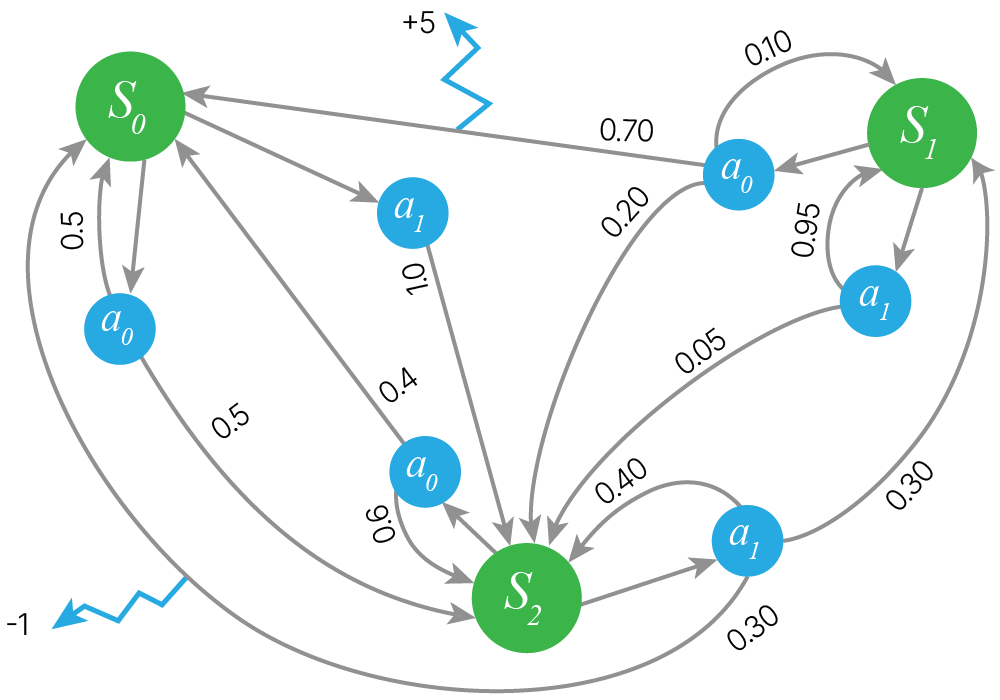
Воспользуемся примером 🐾[git]:
from IPython.display import clear_output
# After this setup we can import mdp package
!wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/setup_colab.sh -O- | bash
!wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/week02_value_based/mdp.py
!touch .setup_complete
clear_output()
from mdp import MDP
transition_probs = {
"s0": {"a0": {"s0": 0.5, "s2": 0.5}, "a1": {"s2": 1}},
"s1": {"a0": {"s0": 0.7, "s1": 0.1, "s2": 0.2}, "a1": {"s1": 0.95, "s2": 0.05}},
"s2": {"a0": {"s0": 0.4, "s2": 0.6}, "a1": {"s0": 0.3, "s1": 0.3, "s2": 0.4}},
}
rewards = {"s1": {"a0": {"s0": +5}}, "s2": {"a1": {"s0": -1}}}
mdp = MDP(transition_probs, rewards, initial_state="s0")
# We can now use MDP just as any other gym environment:
print("initial state =", mdp.reset())
next_state, reward, done, info = mdp.step("a1")
print("next_state = %s, reward = %s, done = %s" % (next_state, reward, done))
initial state = s0 next_state = s2, reward = 0.0, done = False
# MDP methods
print("mdp.get_all_states =", mdp.get_all_states())
print("mdp.get_possible_actions('s1') = ", mdp.get_possible_actions("s1"))
print("mdp.get_next_states('s1', 'a0') = ", mdp.get_next_states("s1", "a0"))
# state, action, next_state
print("mdp.get_reward('s1', 'a0', 's0') = ", mdp.get_reward("s1", "a0", "s0"))
# get_transition_prob(self, state, action, next_state)
print(
"mdp.get_transition_prob('s1', 'a0', 's0') = ",
mdp.get_transition_prob("s1", "a0", "s0"),
)
mdp.get_all_states = ('s0', 's1', 's2')
mdp.get_possible_actions('s1') = ('a0', 'a1')
mdp.get_next_states('s1', 'a0') = {'s0': 0.7, 's1': 0.1, 's2': 0.2}
mdp.get_reward('s1', 'a0', 's0') = 5
mdp.get_transition_prob('s1', 'a0', 's0') = 0.7
from IPython.display import display_jpeg
import mdp as MDP
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
display_jpeg(MDP.plot_graph(mdp))
Наши состояния, очевидно, неравноценны. Давайте к каждому состоянию привяжем награду $R_s$. Она может быть как нулевой, так и положительной либо отрицательной.
Например, в марковском процессе принятия решений (MDP), описывающем игру в шахматы или GO, награда агента может быть положительной только при переходе в состояние "партия выиграна".
На всех остальных ходах награда будет нулевой.
Для перемещающегося робота награда на каждом шаге может быть отрицательной, так как на перемещение требуется энергия и т.п.
Для покера наградой можно назначить изменение текущей суммы игрока после сыгранной раздачи.
Схема для студента в этом случае модифицируется следующим образом. Заметьте, награды тут расставляются с точки зрения актора — студента:

Для турнира по шахматам, где играется 10 партий, финальный reward будет складываться из reward за каждую партию в отдельности.
Если у нас есть тест из 40 вопросов, то опять же, нам не важно, как именно мы получили 30 баллов, главное — мы их получили.
То есть, в таких случаях мы можем считать Return следующим образом:
$$\text{Return} = \sum_i {R_i}$$А теперь представим себе, что мы можем работать 2 года бесплатно и получить разом 5 миллионов рублей. А можем работать 2 года и каждый год получать 70 тысяч.
Или мы можем 6 лет учиться, получая сторонними активностями 20 тысяч в месяц, а затем сразу начать получать 150 тысяч в месяц, а затем и больше. А можем сразу пойти на работу и начать зарабатывать 50 тысяч в месяц, постепенно дойдя до 100.
Что лучше: опубликовать две статьи в журнале с импакт фактором 5 в этом году или одну, но через 2 года и в журнале с импакт-фактором 20?
Что выгоднее?
Очевидно, в таких ситуациях лучше учитывать не только Reward, но и то, когда он получен.
Поэтому при оценке кумулятивной награды на шаге $t$ $(G_t)$ используется коэффициент дисконтирования $\gamma$, который показывает, насколько ценными являются будущие награды на текущий момент (см. Markov Decision Processes (David Silver Lectures) 📚[book]):
$$\large G_t = R_{t+1} + \gamma R_{t+2} + ... =\sum^{\infty}_{k=0} \gamma ^ kR_{t+k+1}, $$где:
При этом:
Какое значение $\gamma$ выбрать?
Можно ли его выбрать равным 1?
Да, мы уже это делали ранее.
Можно ли его выбрать равным 0?
Тоже да. В этом случае у нас получится "жадный" алгоритм: мы всегда выбираем решение, которое дает максимальную награду сейчас, нас не волнуют будущие награды.
Может $\gamma = 0$ привести к проблемам?
Да, например:
Вариант 1: Получить сегодня 1000 рублей.
Вариант 2: Получить завтра 100000 рублей
Обычно, второй вариант более предпочтителен. Но жадный алгоритм его не увидит.
Может $\gamma = 1$ привести к проблемам?
Представим себе генератор шуток про медведя. Большая часть людей знает эту шутку, поэтому было бы хорошо посередине вставлять дополнительные детали — "для ценителей". Но заканчиваться шутка должна одинаково.
Мы решили написать программу, которая генерирует шутки про медведя. Шутка должна начинаться с "Шел медведь по лесу" и заканчиваться "Сел в машину и сгорел". Как бы это описать?
Есть состояния, а модель сама решает, куда ей переходить. Вероятностей мы тут не добавили. Что модель решила, то и будет.
Сразу видим и проблему, которую мы получаем при $\gamma = 1$, пусть и в утрированном виде. Ничто не запрещает нашей модели бесконечно добавлять детали к анекдоту, тем самым увеличивая $G_t$. Работать с такой моделью невозможно.
Если в какой-то момент обучения наша модель стала походить на эту, то ничего осмысленного мы и далее не получим. А вот если введением дискаунта дать модели понять, что слушатели анекдота все же хотят вскоре услышать его конец, то проблема уйдет.
Обычно $0 \le \gamma \le 1$
Обычно $\gamma$ ставят равной чему-то между двумя этими крайностями.
Близость $\gamma$ к 0 отражает нашу "нетерпеливость" — насколько важно получить награду именно сейчас.
Наличие такого $\gamma$ позволяет нам не делать различия между моделями с ограниченным числом шагов и неограниченным: теперь в любом случае return будет конечным числом, т.к. выражение для return ограничено сверху суммой бесконечно убывающей геометрической прогрессии.
Пусть $R_{\max} = \max R_i$ — максимальная награда, которую мы в принципе можем получить в каком-то состоянии.
$\displaystyle G_t = R_{t+1} + \gamma \cdot R_{t+2} + \gamma^2 \cdot R_{t+3} + ... \le R_{\max} + \gamma \cdot R_{\max} + \gamma^2 \cdot R_{\max} + ... = R_{\max} (1 + \gamma + \gamma^2 + ... ) \le R_{\max} \cdot \frac{1}{1-\gamma} = const $
Discounting makes sums finite
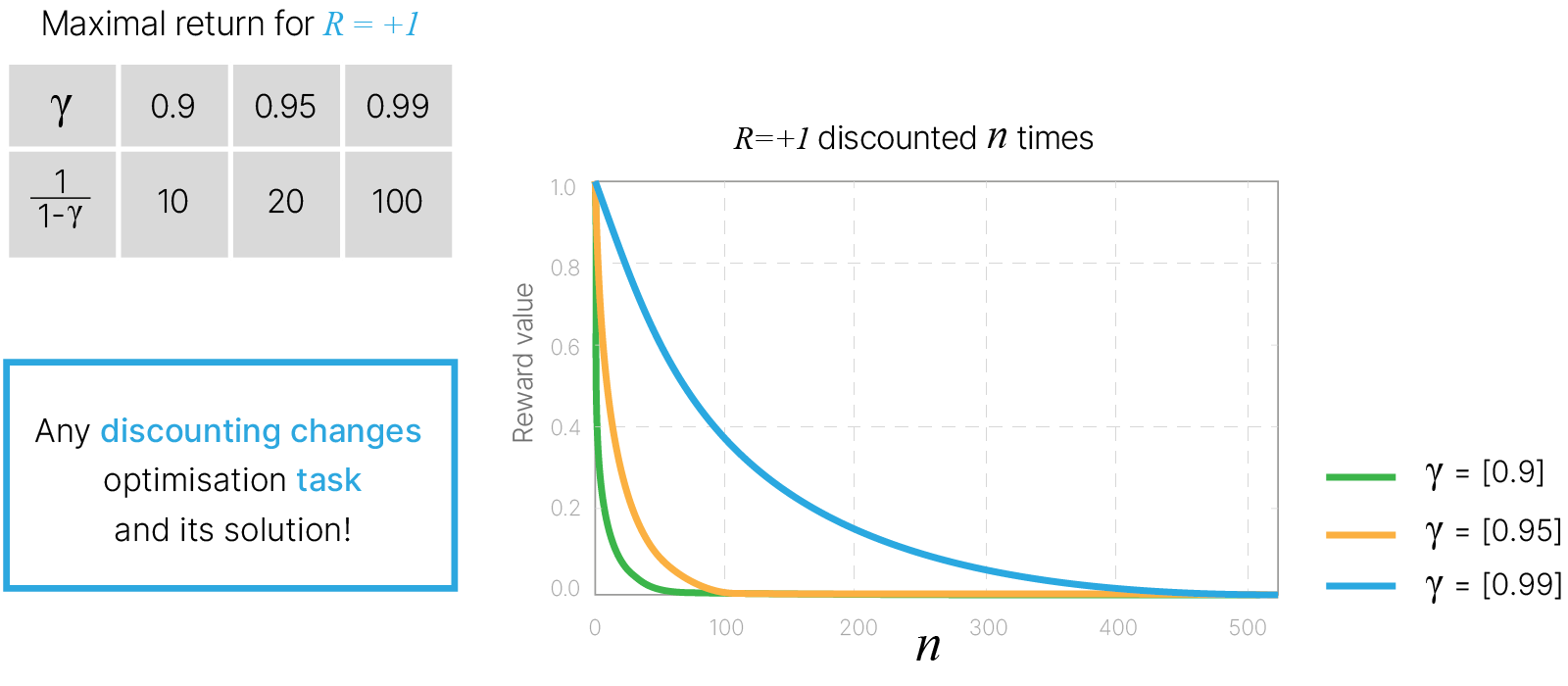
Важно понимать, что выбор $\gamma$ меняет задачу, которую мы решаем, и, соответственно, меняет решение.
Нужно найти последовательность переходов, которой будет соответствовать максимальная награда ($G_t$).
Политика (policy) $\pi$ — это функция, которая для текущего состояния $s$ дает распределение вероятностей на множестве действий $A$.
$$ \large \pi(a|s)=\mathbb{P}\left[A_{t}=a \mid S_{t}=s\right] $$Для нашего примера со студентом:
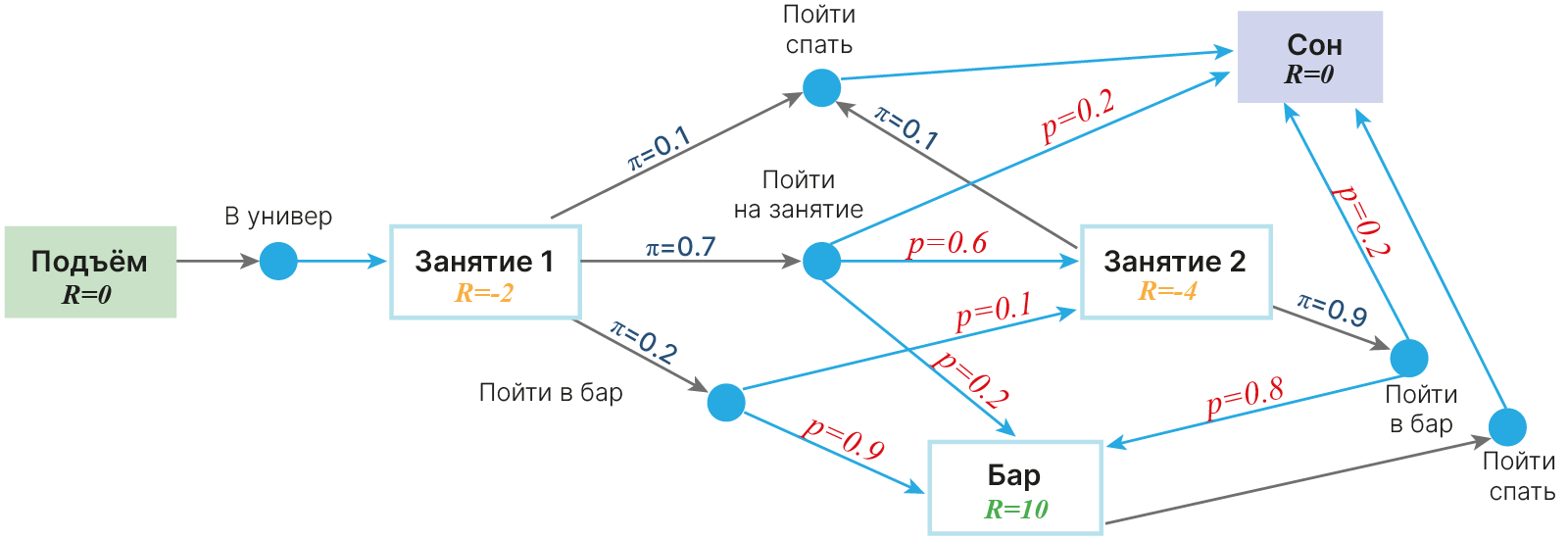
Так, например, агент может следовать политике, заключающейся в переходе между состояниями с высокой ценностью. Однако функция ценности состояния удалена от принятия решений агентом, поскольку агент зачастую не может сам выбрать следующее состояние, в которое перейдет, поскольку на него будет оказываться влияние случайности (например, броски кубиков) или внешних сил (ход оппонента). Поэтому при выборе оптимальной политики рассматривают ценность не состояний, а действий.
Формально V-функция $v_\pi(s)$ вводится в качестве математического ожидания (по политике $\pi$ и по MDP среды $P_{s s^{\prime}}^{a}$) от будущей дисконтированной награды $G_t$, в случае если мы начинаем свои действия в состоянии среды $s$ и будем действовать строго согласно нашей политики $\pi$:
$$\large \begin{equation} \begin{aligned} v_{\pi}(s) &=\mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s\right] \end{aligned} \end{equation}$$Формально Q-функция вводится в качестве математического ожидания от будущей дисконтированной награды $G_t$, в случае если мы находясь в состоянии $s$ выбрали конкретное действие $a$, а все последующие действия совершали строго согласно политике $\pi$:
$$\large \begin{equation} \begin{aligned} q_{\pi}(s, a) &=\mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s \mid A_{t}=a\right]. \end{aligned} \end{equation}$$Сразу отметим, что Q и V функции, очевидно, связаны. Если мы воспользуемся нашей политикой $\pi$ для выбора действия $a$, то сразу же придём к определению V-функции (то есть усредним значения Q-функции согласно вероятностям принятия решений, которые задаёт политика): $$\large \begin{equation} \begin{aligned} \sum_a \pi(a|s) q_{\pi}(s, a) &=\mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s \right]\\ &=v_{\pi}(s). \end{aligned} \end{equation}$$
То есть V-функцию легко записать через Q функцию и политику $\pi$. Обратное соотношение, позволяющее выразить Q функцию через V функцию мы рассмотрим ниже.
Беллман 📚[wiki] показал, что задача динамической оптимизации в дискретном времени может быть сформулирована в рекурсивной пошаговой форме, путем записи связи между функцией ценности в текущий период и функцией ценности в следующем периоде.
где последнее слагаемое можно записать по определению V-функции, учитывая что вероятность перейти из состояния $s$ в возможное состояние $s'$ в момент времени $t$ определяется значением политики $\pi(a|s)$ и MDP средой $P_{s s^{\prime}}^{a}$: $$\large \begin{equation} \begin{aligned} \mathbb{E}_{\pi}\left[\gamma G_{t+1} \mid S_{t}=s\right] = \sum_{a}\pi(a|s)\sum_{s}P_{s s^{\prime}}^{a}\left[{\mathbb{E}_{\pi}\left[\gamma G_{t+1} \mid S_{t+1}=s'\right]}\right] = \sum_{a}\pi(a|s)\sum_{s}P_{s s^{\prime}}^{a}\left[v_{\pi}(s')\right], \end{aligned} \end{equation}$$ что теперь позволяет записать окончательно так называемое уравнение Беллмана: $$\Large \begin{equation} \begin{aligned} v_{\pi}(s) = \mathbb{E}_{\pi}\left[R_{t+1}\right] + \sum_{a}\pi(a|s)\sum_{s}P_{s s^{\prime}}^{a}\left[v_{\pi}(s')\right]. \end{aligned} \end{equation}$$
Уравнение Беллмана - рекуррентное соотношение, позволяющее связать значение V-функции для двух последовательных состояний $s$ и $s'$, если нам известна политика $\pi$ и матрица перехода в MDP $P$. Данное уравнение является ключевым результатом для построения всех последующих RL-алгоритмов.
Представленный выше вывод можно повторить для Q-функции и записать аналогичное рекуррентное соотношение: $$\Large \begin{equation} \begin{aligned} q_{\pi}(s, a) = \mathbb{E}_{\pi}\left[R_{t+1}\right] + \sum_{a}\pi(a|s)\sum_{s}P_{s s^{\prime}}^{a}\left[\sum_{a'}\pi(a'|s')q_{\pi}(s', a')\right]. \end{aligned} \end{equation}$$
Функцию ценности состояния можно представить в виде резервной диаграммы 🎓[article] (backup diagram):
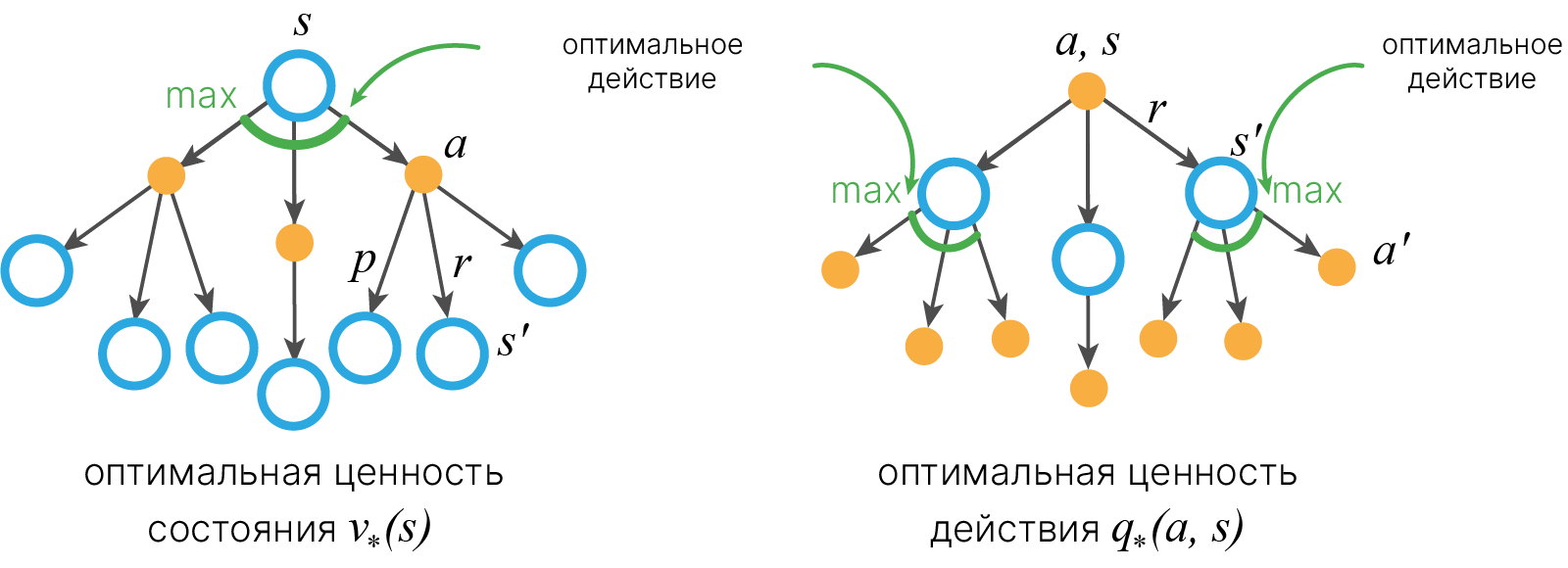
$ \mathbf {s} $ — начальное состояние, из него исходят стрелки, отображающие вероятность совершить то или иное действие в соответствии с политикой $ \mathbf{\pi} $, действия $\mathbf{a}$ обозначаются переходом из кружка в чёрную точку, черные точки обозначают $\mathbf{q} $.
Если раскрыть знак матожидания для награды $R_t$ получим запись системы уравнений наиболее широко используемую в литературе:
$$ \large v_{\pi}(s) = \sum_a\pi(a|s)\sum_{s'}P_{ss'}^{a}(R_{ss'}^{a}+\gamma\mathbb{E}_{\pi}\left[G_{t+1}\mid S_{t+1}=s'\right]) = \sum_a\pi(a|s)\sum_{s'}P_{ss'}^{a}(R_{ss'}^{a}+\gamma v_{\pi}(s')). $$Аналогично для функции ценности действия:
$$ \large q_{\pi}(s, a) = \sum_{s'}P_{ss'}^{a}(R_{ss'}^{a}+\gamma\sum_{a'}\pi(a'|s') q_{\pi}(s', a')) = \sum_{s'}P_{ss'}^{a}(R_{ss'}^{a}+\gamma \large v_{\pi}(s')). $$Важно отметить, что описанные выше рекуррентные соотношения выполняются в том числе и для оптимального выбора политики $\pi$, к поиску которого мы и стремимся. Для этого воспользуемся ещё одной идеей, которая лежит в определении V и Q функций.
Принцип оптимальности Беллмана
Беллманом был сформулирован принцип, позволяющий из анализа выписанных выше рекуррентных соотношений определить оптимальную политику принятия решений в MDP.
Оптимальная политика обладает тем свойством, что какими бы ни были начальное состояние и начальное действие, остальные действие должны представлять собой оптимальную политику в отношении состояния, полученного в результате первого действия. (Bellman, 1957, Chap. III.3.)

Ценность (Value) $v$ в состоянии $s$ — это $v_{\pi}(s)$
Из состояния $s$ агент может сделать 3 действия: $(a_1, a_2, a_3)$
Ценность действия (Action Value) — это $v_{\pi}(s,a)$, где $a = \{a_1, a_2, a_3\}$
Агент предпринял действие $a_3$. А так он может перейти в состояния $s’_1$, $s’_2$ или $s’_3$ с вероятностью перехода p1, p2 или p3 соответственно
Полученная награда — $r_1$, $r_2$ или $r_3$ в зависимости от текущего состояния
Понять это несколько громоздкое определение можно последовательно задав следующие вопросы:
Оптимальным решением для любого узла графа MDP, очевидно, будет такой выбор стратегии принятия решений $a$, при котором матожидание будущей дисконтированной награды будет максимально. Будущую дисконтированную награду измеряет функция V. То есть $\pi^*$ - оптимальная политика, если среди всех допустимых уравнением Беллмана V-функций $v_{\pi^*}$ такая, что для любого $s$ она принимает максимально возможное значение ($v_{\pi^{*}}(s) \rightarrow max$)
Вместо того, чтобы рассчитывать ценность состояния $ \mathbf{s}$ на основе ценности всех состояний $ \mathbf{s'}$, в которые мы можем перейти, мы можем рассчитать ценность состояния, учитывая ценность всех действий $\mathbf{a}$, которые мы можем совершить, находясь в состоянии $\mathbf{s}$. Получаем таким образом выражение одной функции через другую:
$$\large v_{\pi}(s) = \sum_a\pi(a|s)q_{\pi}(s,a).$$Для этого мы ввели Q-функцию. В случае нахождения оптимальной политики $q_{\pi^{*}}$ лучшим с точки зрения матожидания награды будет выбор действия $\text{argmax}_a q_{\pi^{*}}(s,a)$. Отсюда сразу следует, что в случае оптимальной игры максимальное значение V функции достигается на максимальном значении Q функции: $$\large v_{\pi^*}(s) = \max_{a(s)}q_{\pi^*}(s,a) = \max_{a(s)}\sum_{s'}P_{ss'}^{a}(R_{ss'}^{a}+\gamma v_{\pi^*}(s')).$$
Отсюда сразу следует основной результат для Беллман-оптимальной политики $\pi^*$: $$\large \pi^*(s) = \text{argmax}_aq_*(s,a)$$
Примечание: $\text{argmax}$ может быть заменен на $\text{softmax}$, если матрица перехода MDP явно зависит от $a$.
Возьмём рассмотренные выше уравнения Беллмана и определим с их помощью оператор $\mathcal{T}$ по его действию на $V$ и $Q$ функции:
$$\large \mathcal{T}[\color{red}{v}](s) = \sum_a\pi(a|s)\sum_{s'}P_{ss'}^{a}(R_{ss'}^{a}+\gamma \color{red}{v(s')}),$$$$\large \mathcal{T}[\color{red}{q}](s,a) = \sum_{s'}P_{ss'}^{a}(R_{ss'}^{a}+\gamma\sum_{a'}\pi(a'|s') \color{red}{q(s', a')}).$$Как подробно показано в Reinforcement Learning: An Introduction 📚[book], такой оператор $\mathcal{T}$ является сжимающим. То есть если взять любую пару функций $V_1$ и $V_2$, найдётся такое неотрицательное число $C$, что:
$$\large || \mathcal{T}[V_1] - \mathcal{T}[V_2]|| \leq C||V_1 - V_2||,$$что означает, что после применения оператора $\mathcal{T}$ функции $V_1$ и $V_2$ становятся ближе друг к другу.
По теореме о неподвижной точке 📚[wiki] это означает, что существует как минимум одна функция, которая не изменяется оператором $\mathcal{T}$. Так как мы построили наш оператор как правую часть уравнения Беллмана, то эта неподвижная точка — искомое нами решение. Отсюда появляется идея итеративного поиска решения для функций $Q$ или $V$:
Весь процесс поиска оптимальной политики можно разделить на два этапа.
Policy evaluation
Фиксируем произвольную политику $\pi$ и V-функцию $V_0$. Проведём итерационную процедуру с оператором $\large \mathcal{T}[\color{red}{v}](s)$, пока не сойдёмся к неподвижной точке.
Policy improvement
Теперь мы знаем правило $v$ для нашей политики. Как нам его улучшить? Будем в каждом состоянии менять нашу политику таким образом, чтобы мы шли в состояние с лучшим $q$. Мы могли бы улучшить это, действуя жадно $\mathrm{q}(\mathrm{s}, \mathrm{a}) !$ $$ \large \pi^{\prime}(s) \leftarrow \underset{a}{\arg \max } \overbrace{\sum_{r, s^{\prime}} P_{ss'}^a\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right]}^{q_{\pi}(s, a)} $$
Эта процедура гарантированно приведет к улучшению политики!
$$ \large \begin{equation} \begin{aligned} &\text { если } \quad q_{\pi}\left(s, \pi^{\prime}(s)\right) \geq v_{\pi}(s) \quad \text { для всех состояний, } \\ &\text { тогда } \quad v_{\pi^{\prime}}(s) \geq v_{\pi}(s) \text { означает, } \\ &\text { что } \qquad \pi^{\prime} \geq \pi . \end{aligned} \end{equation} $$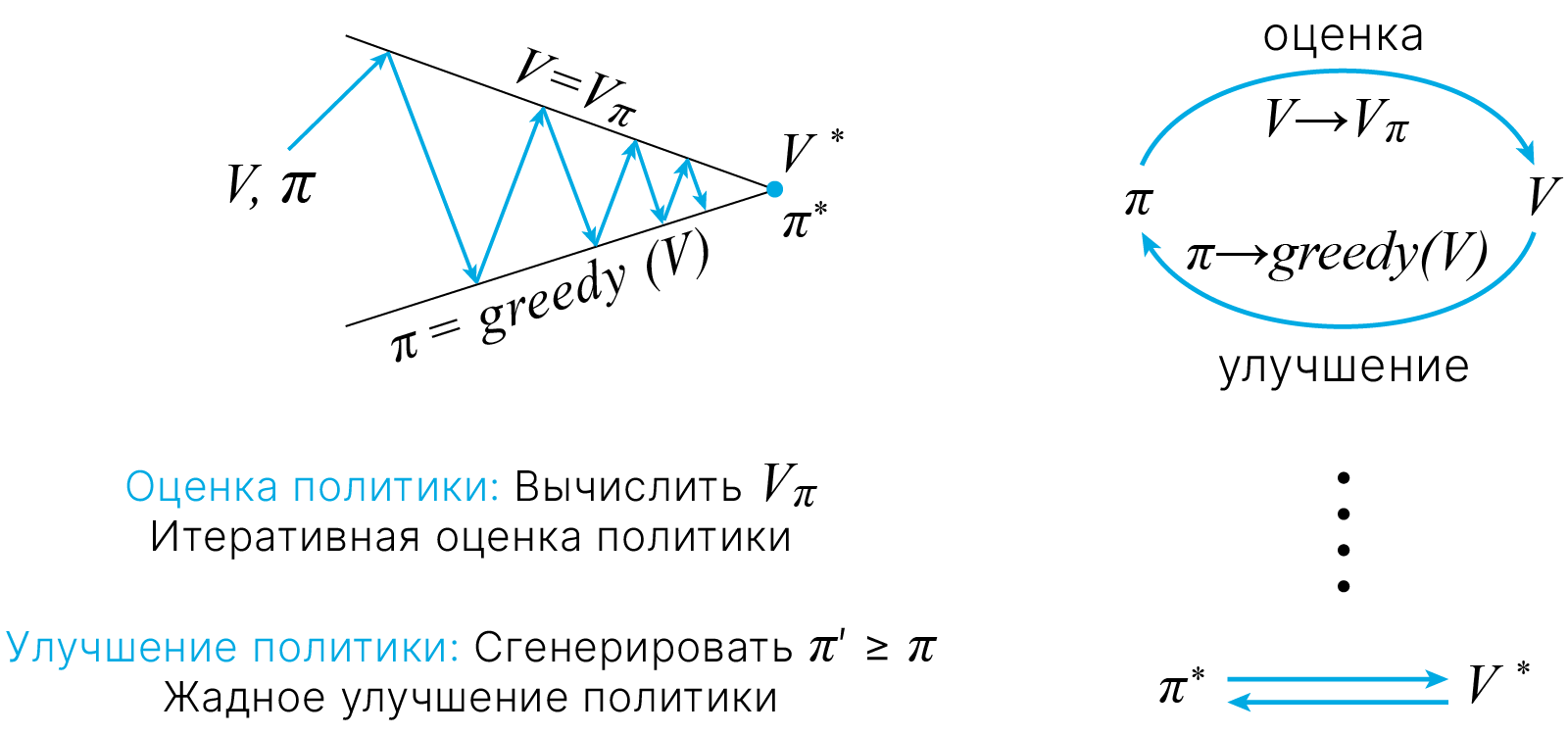
Метод действительно сходится:
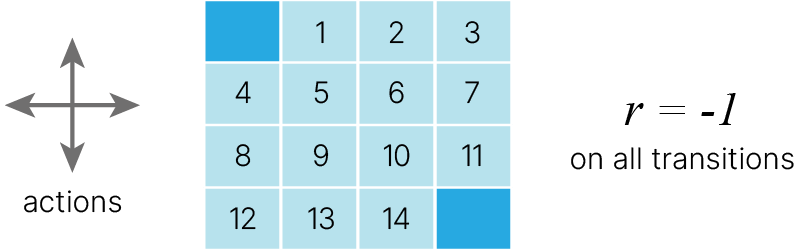
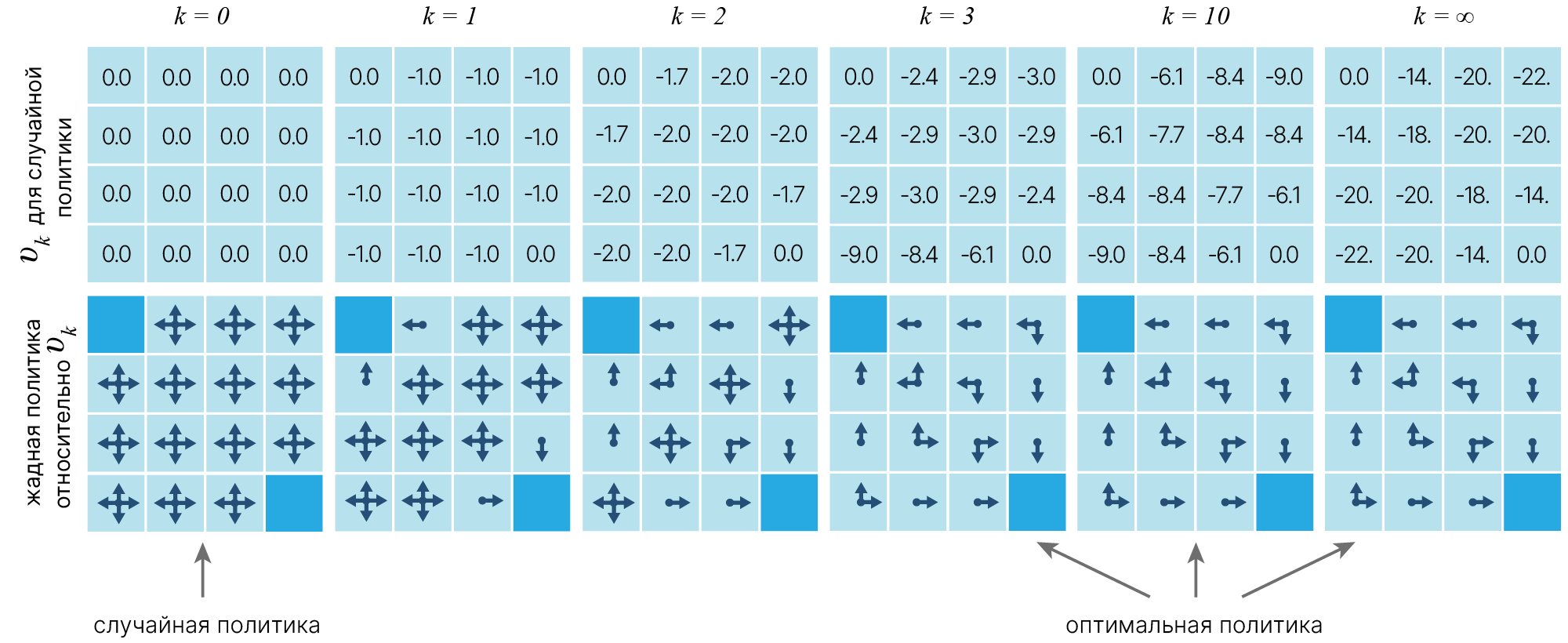
Фактически этап policy evaluation от policy iteration может быть сокращен различными способами без потери гарантий сходимости policy iteration.
Один важный особый случай — это когда оценка политики останавливается сразу после одного цикла (одно обновление каждого состояния). Этот алгоритм называется value iteration. Его можно записать как простую операцию обновления, которая сочетает в себе этапы улучшения политики и усеченной policy evaluation (один шаг).
Это позволяет, в частности, вообще не записывать политику в явном виде, т.к. она однозначно определяется Q-функцией.
Value iteration (VI) vs. Policy iteration (PI):
Проведем эксперимент с каким-то количеством шагов для нахождения лучшей политики.
Алгоритм
*В отличие от Policy iteration, сама политика в памяти не хранится, она генерируется при помощи Q-функции.
Теперь давайте построим что-нибудь, чтобы решить эту MDP.
Запишем решения для этого MDP. Самый простой алгоритм — это Value Iteration.
Псевдо код для VI:
1. Initialize $V^{(0)}(s)=0$, for all $s$
2. For $i=0, 1, 2, \dots$
3. $ \quad V_{(i+1)}(s) = \max_a \sum_{s'} P_{ss'}^a \cdot [ R_{ss'}^a + \gamma V_{i}(s')]$, for all $s$
$R_{ss'}^a$ — награда, соответствующая выбору действия a в s,
$s$ — исходное состояние,
$s'$ — новое состояние.
Функция для вычисления функции значения состояния-действия $Q^{\pi}$ определяется следующим образом:
$$\large Q_i(s, a) = \sum_{s'} P_{ss'}^a \cdot [ R_{ss'}^a + \gamma V_{i}(s')],$$$s'$ — зависит от вероятности перехода.
def get_action_value(mdp, state_values, state, action, gamma):
"""
Computes Q(s,a) as in formula above
mdp : MDP object
state_values : dictionayry of { state_i : V_i }
state: string id of current state
gamma: float discount coeff
"""
next_states = mdp.get_next_states(state, action)
Q = 0.0
for next_state in next_states.keys():
# alternatively p = mdp.get_transition_prob(state, action, next_state)
p = next_states[next_state]
Q += p * (
mdp.get_reward(state, action, next_state) + gamma * state_values[next_state]
)
return Q
Используя $Q(s,a)$, мы можем определить "следующее" V(s) для VI:
$$\large V_{(i+1)}(s) = \max_a \sum_{s'} P_{ss'}^a \cdot [ R_{ss'}^a + \gamma V_{i}(s')] = \max_a Q_i(s,a)$$def get_new_state_value(mdp, state_values, state, gamma):
"""Computes next V(s) as in formula above. Please do not change state_values in process."""
if mdp.is_terminal(state):
return 0 # Game over
q_max = float("-inf")
actions = mdp.get_possible_actions(state)
for a in actions:
q = get_action_value(mdp, state_values, state, a, gamma)
q_max = max(q_max, q)
return q_max
Наконец, объединим все, что мы написали, в алгоритм итерации рабочего значения.
# parameters
gamma = 0.9 # discount for MDP
num_iter = 100 # maximum iterations, excluding initialization
# stop VI if new values are this close to old values (or closer)
min_difference = 0.001
# initialize V(s)
state_values = {s: 0 for s in mdp.get_all_states()}
display_jpeg(MDP.plot_graph_with_state_values(mdp, state_values))
Здесь нет никакого "текущего состояния"! Добавим матрицу состояний и построим новый граф:
for i in range(num_iter):
# Compute new state values using the functions you defined above.
# It must be a dict {state : float V_new(state)}
new_state_values = {}
for s in state_values.keys():
new_state_values[s] = get_new_state_value(mdp, state_values, s, gamma)
# Compute difference
diff = max(abs(new_state_values[s] - state_values[s]) for s in mdp.get_all_states())
print("iter %4i | diff: %6.5f | " % (i, diff), end="")
print(" ".join("V(%s) = %.3f" % (s, v) for s, v in state_values.items()))
state_values = new_state_values
if diff < min_difference:
print("Terminated")
break
iter 0 | diff: 3.50000 | V(s0) = 0.000 V(s1) = 0.000 V(s2) = 0.000 iter 1 | diff: 0.64500 | V(s0) = 0.000 V(s1) = 3.500 V(s2) = 0.000 iter 2 | diff: 0.58050 | V(s0) = 0.000 V(s1) = 3.815 V(s2) = 0.645 iter 3 | diff: 0.43582 | V(s0) = 0.581 V(s1) = 3.959 V(s2) = 0.962 iter 4 | diff: 0.30634 | V(s0) = 0.866 V(s1) = 4.395 V(s2) = 1.272 iter 5 | diff: 0.27571 | V(s0) = 1.145 V(s1) = 4.670 V(s2) = 1.579 iter 6 | diff: 0.24347 | V(s0) = 1.421 V(s1) = 4.926 V(s2) = 1.838 iter 7 | diff: 0.21419 | V(s0) = 1.655 V(s1) = 5.169 V(s2) = 2.075 iter 8 | diff: 0.19277 | V(s0) = 1.868 V(s1) = 5.381 V(s2) = 2.290 iter 9 | diff: 0.17327 | V(s0) = 2.061 V(s1) = 5.573 V(s2) = 2.481 iter 10 | diff: 0.15569 | V(s0) = 2.233 V(s1) = 5.746 V(s2) = 2.654 iter 11 | diff: 0.14012 | V(s0) = 2.389 V(s1) = 5.902 V(s2) = 2.810 iter 12 | diff: 0.12610 | V(s0) = 2.529 V(s1) = 6.042 V(s2) = 2.950 iter 13 | diff: 0.11348 | V(s0) = 2.655 V(s1) = 6.168 V(s2) = 3.076 iter 14 | diff: 0.10213 | V(s0) = 2.769 V(s1) = 6.282 V(s2) = 3.190 iter 15 | diff: 0.09192 | V(s0) = 2.871 V(s1) = 6.384 V(s2) = 3.292 iter 16 | diff: 0.08272 | V(s0) = 2.963 V(s1) = 6.476 V(s2) = 3.384 iter 17 | diff: 0.07445 | V(s0) = 3.045 V(s1) = 6.558 V(s2) = 3.467 iter 18 | diff: 0.06701 | V(s0) = 3.120 V(s1) = 6.633 V(s2) = 3.541 iter 19 | diff: 0.06031 | V(s0) = 3.187 V(s1) = 6.700 V(s2) = 3.608 iter 20 | diff: 0.05428 | V(s0) = 3.247 V(s1) = 6.760 V(s2) = 3.668 iter 21 | diff: 0.04885 | V(s0) = 3.301 V(s1) = 6.814 V(s2) = 3.723 iter 22 | diff: 0.04396 | V(s0) = 3.350 V(s1) = 6.863 V(s2) = 3.771 iter 23 | diff: 0.03957 | V(s0) = 3.394 V(s1) = 6.907 V(s2) = 3.815 iter 24 | diff: 0.03561 | V(s0) = 3.434 V(s1) = 6.947 V(s2) = 3.855 iter 25 | diff: 0.03205 | V(s0) = 3.469 V(s1) = 6.982 V(s2) = 3.891 iter 26 | diff: 0.02884 | V(s0) = 3.502 V(s1) = 7.014 V(s2) = 3.923 iter 27 | diff: 0.02596 | V(s0) = 3.530 V(s1) = 7.043 V(s2) = 3.951 iter 28 | diff: 0.02336 | V(s0) = 3.556 V(s1) = 7.069 V(s2) = 3.977 iter 29 | diff: 0.02103 | V(s0) = 3.580 V(s1) = 7.093 V(s2) = 4.001 iter 30 | diff: 0.01892 | V(s0) = 3.601 V(s1) = 7.114 V(s2) = 4.022 iter 31 | diff: 0.01703 | V(s0) = 3.620 V(s1) = 7.133 V(s2) = 4.041 iter 32 | diff: 0.01533 | V(s0) = 3.637 V(s1) = 7.150 V(s2) = 4.058 iter 33 | diff: 0.01380 | V(s0) = 3.652 V(s1) = 7.165 V(s2) = 4.073 iter 34 | diff: 0.01242 | V(s0) = 3.666 V(s1) = 7.179 V(s2) = 4.087 iter 35 | diff: 0.01117 | V(s0) = 3.678 V(s1) = 7.191 V(s2) = 4.099 iter 36 | diff: 0.01006 | V(s0) = 3.689 V(s1) = 7.202 V(s2) = 4.110 iter 37 | diff: 0.00905 | V(s0) = 3.699 V(s1) = 7.212 V(s2) = 4.121 iter 38 | diff: 0.00815 | V(s0) = 3.708 V(s1) = 7.221 V(s2) = 4.130 iter 39 | diff: 0.00733 | V(s0) = 3.717 V(s1) = 7.230 V(s2) = 4.138 iter 40 | diff: 0.00660 | V(s0) = 3.724 V(s1) = 7.237 V(s2) = 4.145 iter 41 | diff: 0.00594 | V(s0) = 3.731 V(s1) = 7.244 V(s2) = 4.152 iter 42 | diff: 0.00534 | V(s0) = 3.736 V(s1) = 7.249 V(s2) = 4.158 iter 43 | diff: 0.00481 | V(s0) = 3.742 V(s1) = 7.255 V(s2) = 4.163 iter 44 | diff: 0.00433 | V(s0) = 3.747 V(s1) = 7.260 V(s2) = 4.168 iter 45 | diff: 0.00390 | V(s0) = 3.751 V(s1) = 7.264 V(s2) = 4.172 iter 46 | diff: 0.00351 | V(s0) = 3.755 V(s1) = 7.268 V(s2) = 4.176 iter 47 | diff: 0.00316 | V(s0) = 3.758 V(s1) = 7.271 V(s2) = 4.179 iter 48 | diff: 0.00284 | V(s0) = 3.762 V(s1) = 7.275 V(s2) = 4.183 iter 49 | diff: 0.00256 | V(s0) = 3.764 V(s1) = 7.277 V(s2) = 4.185 iter 50 | diff: 0.00230 | V(s0) = 3.767 V(s1) = 7.280 V(s2) = 4.188 iter 51 | diff: 0.00207 | V(s0) = 3.769 V(s1) = 7.282 V(s2) = 4.190 iter 52 | diff: 0.00186 | V(s0) = 3.771 V(s1) = 7.284 V(s2) = 4.192 iter 53 | diff: 0.00168 | V(s0) = 3.773 V(s1) = 7.286 V(s2) = 4.194 iter 54 | diff: 0.00151 | V(s0) = 3.775 V(s1) = 7.288 V(s2) = 4.196 iter 55 | diff: 0.00136 | V(s0) = 3.776 V(s1) = 7.289 V(s2) = 4.197 iter 56 | diff: 0.00122 | V(s0) = 3.778 V(s1) = 7.291 V(s2) = 4.199 iter 57 | diff: 0.00110 | V(s0) = 3.779 V(s1) = 7.292 V(s2) = 4.200 iter 58 | diff: 0.00099 | V(s0) = 3.780 V(s1) = 7.293 V(s2) = 4.201 Terminated
display_jpeg(MDP.plot_graph_with_state_values(mdp, state_values))
Теперь воспользуемся этим $V^{*}(s)$, чтобы найти оптимальные действия в каждом состоянии:
$$\pi^*(s) = \text{argmax}_a \sum_{s'} P_{ss'}^a \cdot [ R_{ss'}^a + \gamma V_{i}(s')] = \text{argmax}_a Q_i(s,a)$$
Единственное отличие от $V(s)$ в том, что здесь мы берем не $\max$, а $\text{argmax}$: найти действие с максимальным $Q(s,a)$.
def get_optimal_action(mdp, state_values, state, gamma=0.9):
"""Finds optimal action using formula above."""
if mdp.is_terminal(state):
return None
best_action = None
q_max = float("-inf")
actions = mdp.get_possible_actions(state)
for a in actions:
q = get_action_value(mdp, state_values, state, a, gamma)
if q > q_max:
best_action = a
q_max = q
return best_action
display_jpeg(
MDP.plot_graph_optimal_strategy_and_state_values(
mdp, state_values, get_action_value
)
)
import numpy as np
# Measure agent's average reward
s = mdp.reset()
rewards = []
for _ in range(10000):
s, r, done, _ = mdp.step(get_optimal_action(mdp, state_values, s, gamma))
rewards.append(r)
print("average reward: ", np.mean(rewards))
assert 0.40 < np.mean(rewards) < 0.55
average reward: 0.4532
Итак, в тех случаях, когда известна вероятность $P_{ss'}^a$, задача обучения может быть решена с помощью методов динамического программирования, как было рассмотрено выше. В реальных же задачах динамика среды зачастую неизвестна. Два главных подхода, позволяющие обходить незнание динамики среды, включают метод Монте Карло (MC) и temporal difference (TD)-обучение (TD-learning). Оба эти подхода основываются на симулировании опыта взаимодействия со средой в виде траекторий (MDP trajectory).
MDP trajectory
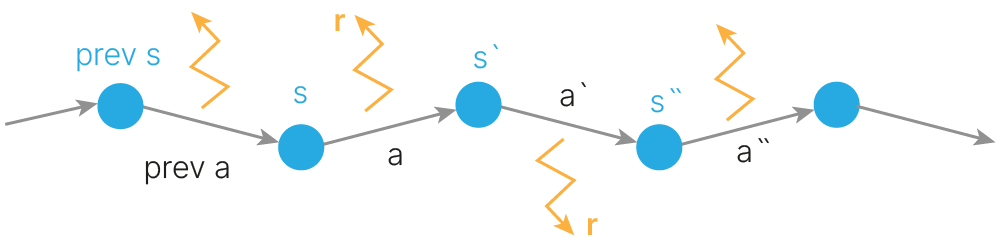
Траектория представляет из себя последовательность
• states ($s$) • actions ($a$) • rewards ($r$)
При этом MC оперирует полными траекториями, оканчивающимися в терминальном состоянии, а TD-learning позволяет учиться на неполных эпизодах, не дожидаясь конечного состояния.
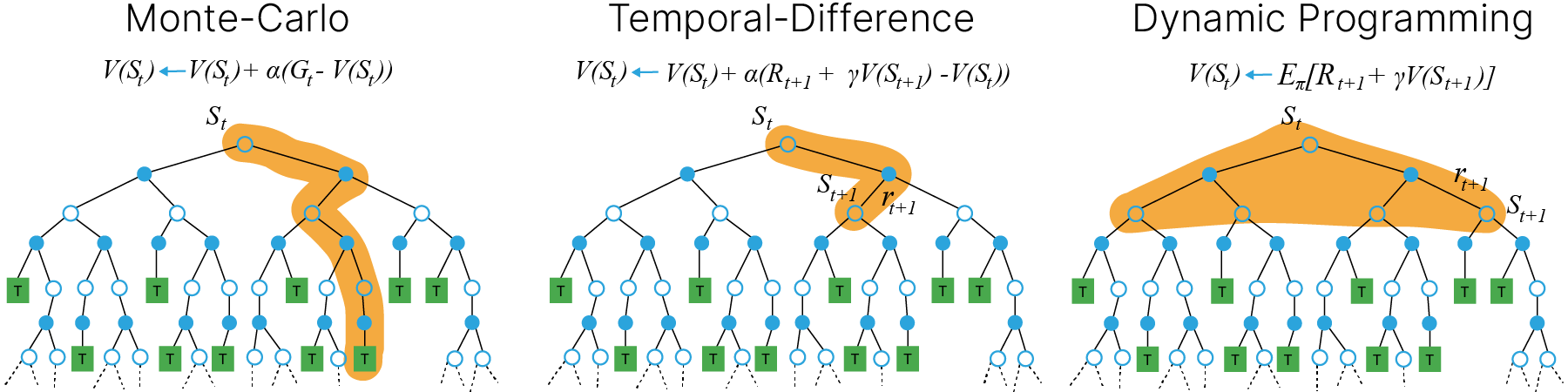
Рассмотрим второй подход подробнее.
TD-learning — один из наиболее мощных подходов, используемых во многих алгоритмах RL. Смысл в том, чтобы обновлять оценки ценности (состояния или действия) на основе уже обученных оценок для последующих состояний. Эту процедуру можно представить как "подтягивание" значения функции ценности того состояния, в котором мы находились на предыдущем шаге, к значению функции ценности того состояния, в котором мы находимся сейчас. Каким образом это можно сделать?
Базовый алгоритм TD-обучения — $TD(0)$ заключается в следующем:
Инициализируем функцию ценности, например, $V(s)$, и стратегию $\pi$. Пусть, у нас есть текущее состояние $s$ из которого мы:
При оптимальной политике $\pi$: $$\overbrace{r+\gamma V(s')}^{\text{TD target}} = \overbrace{V(s)}^{\text{old estimate}}$$
Cоответственно, их разницу, называемую TD-ошибкой (TD-error), мы и будем пытаться минимизировать.
Почему это работает? Ведь мы обучаем случайно инициализированную оценку $V(s)$ на основе других оценок $V(s')$, которые также были инициализированы случайно. Дело в том, что состояния, которые предшествуют получению реальных наград (например, за победу) будут обучаться первыми и затем распространять свою ценность на состояния, предшествующие им.
Стоит отметить также, что TD-обучение не обязательно всегда будет смотреть на один шаг вперед. Алгоритм, называемый $TD(\lambda)$, будет обновлять оценки функции ценности сразу на несколько шагов назад.
Разновидностями TD-обучения являются алгоритмы Q-learning и SARSA.
Матрица перехода $P_{ss'}^{a}$ может быть нам неизвестна явно, что затруднит прямое применение алгоритма динамического программирования для нахождения Q или V функций в общем случае: $$ \large q_{\pi}(s, a) = \sum_{s'}P_{ss'}^{a}(R_{ss'}^{a}+\gamma\sum_{a'}\pi(a'|s') q_{\pi}(s', a')) = \mathbb{E}(R_{ss'}^a +\gamma \mathbb{E}_{\pi} q_{\pi}(s', a')). $$
Мы можем обойти это ограничение, заменив "честное" матожидание по MDP, на выборочное среднее от серии наблюдений вдоль различных траекторий процесса:
$$ \large q_{\pi}(s, a) = \frac{1}{N}\sum_n(R_{ss'}^a +\gamma \mathbb{E}_{\pi} q_{\pi}(s', a')). $$Допустим, мы ходим по полю размером 12×4. Наша цель — попасть в ячейку (3,11). Максимизируя сумму будущих наград, мы также находим самый быстрый путь к цели, поэтому наша цель сейчас — найти способ сделать это!
Начнем с построения таблицы, которая измеряет, насколько хорошо будет выполнить определенное действие в любом состоянии (чем больше значение, тем лучше действие).
Оптимальная «Q-table» имеет значения, которые позволяют нам предпринимать лучшие действия в каждом состоянии, давая нам в итоге лучший путь к победе.
Q-learning — это алгоритм, который «изучает» эти значения. На каждом шагу мы получаем больше информации о мире. Эта информация используется для обновления значений в таблице.
Итак, мы не знаем вероятности переходов. Мы можем только генерировать траектории и учиться на них.

Возникает вопрос, какую из функций ценности нам лучше пытаться учить: $V(s)$ или $Q(s,a)$? Поскольку $V(s)$ не позволит определять политику без знания $P_{ss'}^a$, будет выгоднее учить $Q(s,a)$.
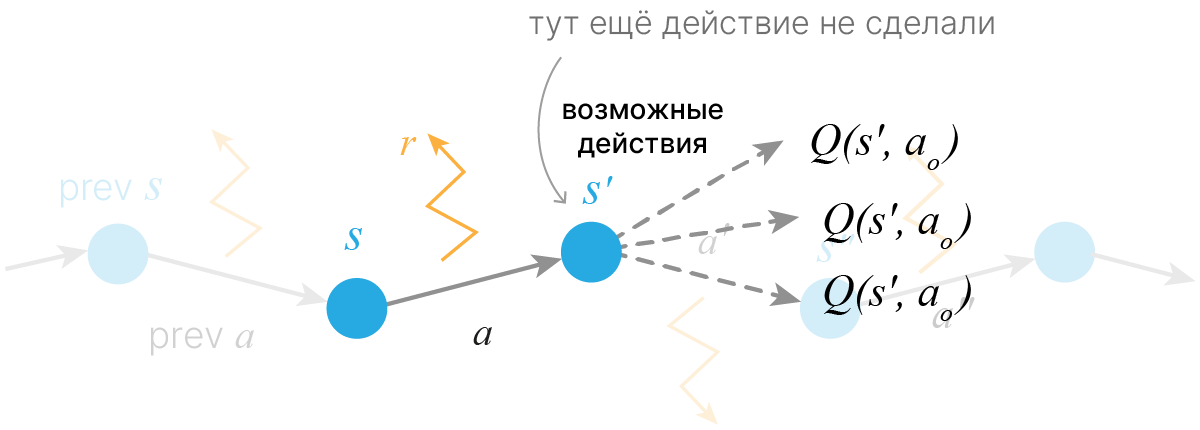
Инициализировать таблицу $Q(s, a)$ нулями.
$\color{red}\triangle$ Мы хотим несмещённую оценку с меньшей дисперисей, поэтому используем скользящее среднее.
$\color{red}\triangle$ Пересчёт функции (поле в таблице) выполняется после перехода.
$\hat{Q}$ — расчетное значение, $Q$ — то, что было в таблице, $\alpha$ — шаг обучения.
Данный алгоритм называется Q-learning. Он напрямую аппроксимирует функцию $q_*(s,a)$, которая фактически представляет оптимальную политику $\pi_*$. В данном алгоритме оценка $Q(s, a)$ обновляется в соответствии с правилами TD-обучения:
$$\large Q(s,a) := Q(s,a) + \alpha(R_{ss'}^a+\gamma\max_{a'}Q(s',a') -Q(s,a))$$Видно, что за счет максимума Q-learning будет аппроксимировать именно $q_*(s,a)$, независимо от того, какой политики мы придерживаемся (которая может быть, например $\varepsilon$-жадной). Наш вариант Q-learning не учитывает того, что мы хотим иногда "рандомить". В совокупности группа методов, при которых мы можем придерживаться абсолютно любой стратегии, а обучаться все равно будут правильные оптимальные значения политики, называется off-policy.
Есть задачи, где количество состояний и переходов огромно, и поддерживать таблицу значений не представляется возможным.
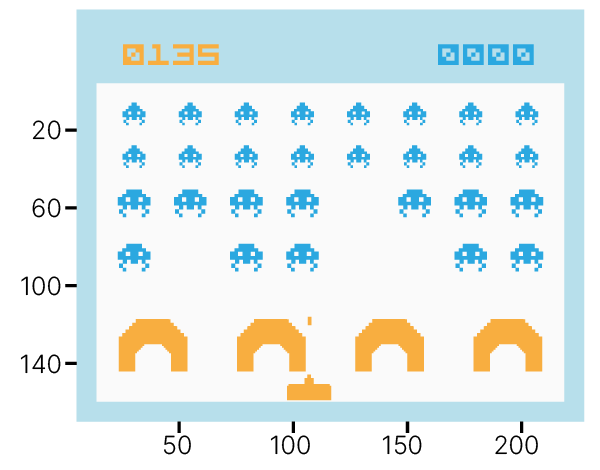
Количество состояний для $8$-мибитной цветной ($3$ RGB-канала) игры Space Invaders с размером игрового поля $210 \times 160$ пикселей:
$$\large |S| = 210\times160\times2^{8\times3}$$В таких ситуациях Q-функцию не считают в явном виде, а аппроксимируют нейросетью.
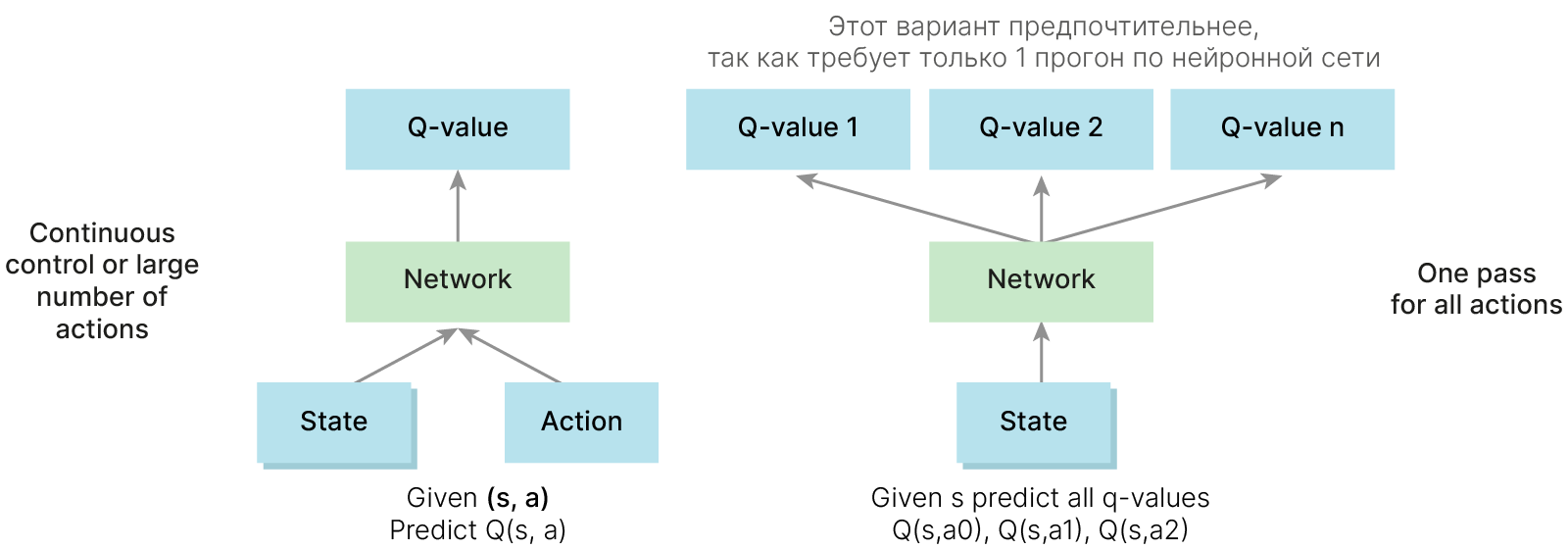
Чтобы считать градиент, приходится принимать значение Q-функции фиксированным и не зависящим от параметров нашей нейросети. Что, конечно, не так.
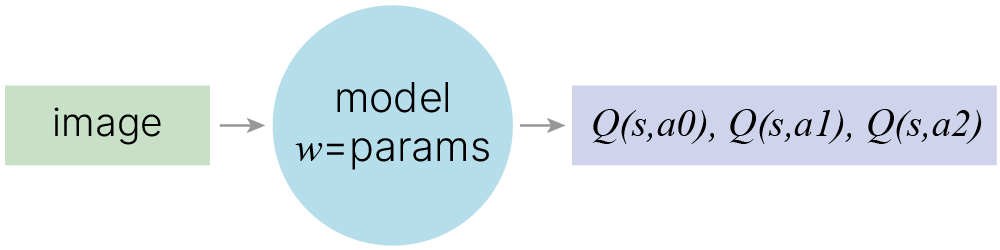
Q-values: $$ \large \hat{Q}\left(s_{t}, a_{t}\right)=r+\gamma \cdot \max _{a^{\prime}} Q\left(s_{t+1}, a^{\prime}\right) $$ Objective: $$ \large L=\left(Q\left(s_{t}, a_{t}\right)-\left[r+\gamma \cdot \max _{a^{\prime}} Q\left(s_{t+1}, a^{\prime}\right)\right]\right)^{2} $$ Gradient step: $$ \large w_{t+1}=w_{t}-\alpha \cdot \frac{\delta L}{\delta w} $$
Basic deep Q-learning
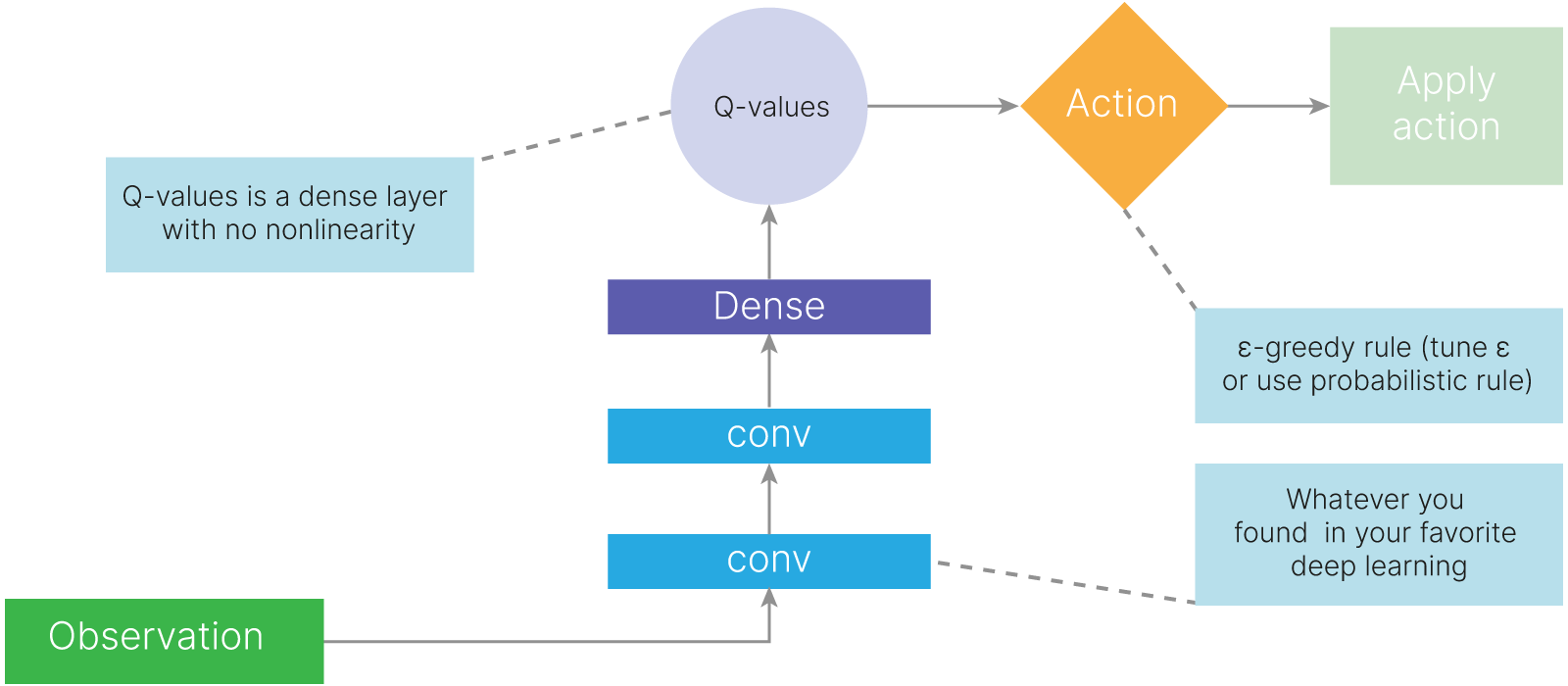
$\varepsilon -greedy$ нужна для исследования среды
Проблема:
В большинстве окружений информация, получаемая агентом, распределена не независимо. Т.е. последовательные наблюдения агента сильно коррелированы между собой (что понятно из интуитивных соображений, т.к. большинство окружений, в которых применяется RL, предполагают, что все изменения в них последовательны).
Мы можем столкнуться с такой проблемой при обучении нейросети, если в игре есть большое количество стандартных персонажей и редко встречающиеся "боссы". После повторения большого количества типовых действий нейросеть будет забывать, как проходить боссов.
Корреляция примеров ухудшает сходимость стохастического градиентного спуска. Таким образом, нам нужен способ, который позволяет улучшить распределение примеров для обучения (устранить или снизить корреляцию между ними).
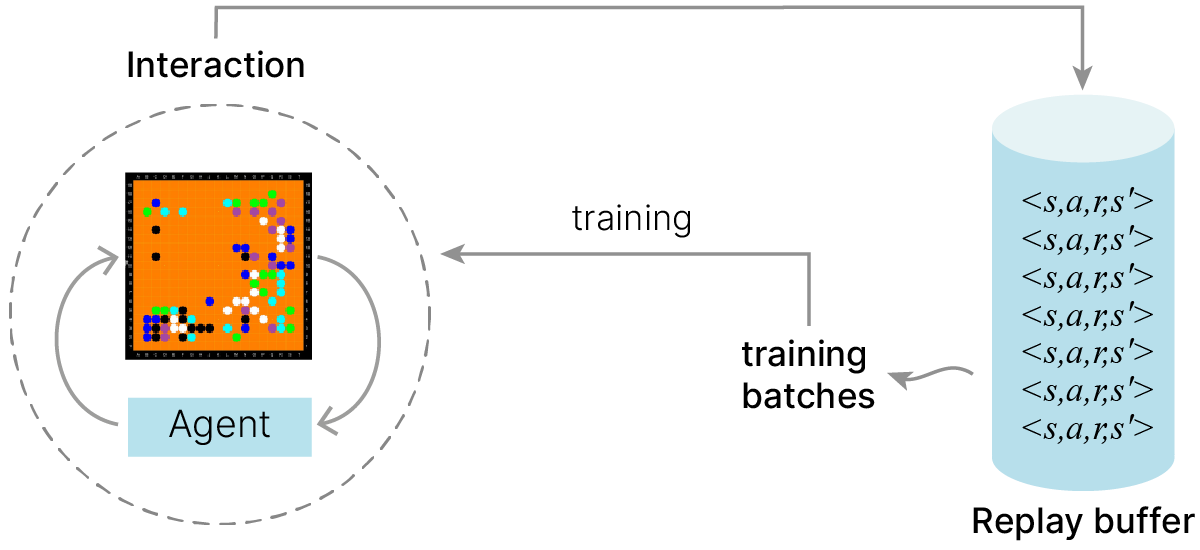
Идея: сохранять несколько предыдущих взаимодействий $<s,a,r,s^{'}>$.
Обучать на случайных подвыборках.
Процесс обучения:
Profit: не требуется заново возвращаться в те же пары состояние-действие $(s,a)$, чтобы выучить их.
$\color{red}\triangle$ Работает только с алгоритмами без политик.
Обычно используется метод проигрывания опыта (experience replay). Суть этого метода в том, что мы сохраняем некоторое количество примеров (состояние, действия, вознаграждение) в специальном буфере и для обучения выбираем случайные мини-батчи из этого буфера.
Так же experience replay позволяет агенту эффективнее использовать свой прошлый опыт.
В DQN для эффективного обучения должны использоваться две сети: одна непосредственно обучается, другая определяет цель (TD target). Почему мы не можем пользоваться одной и той же сетью для получения оценки текущего $Q(s', a')$ и предыдущего $Q(s, a)$ состояний?
Напомним, что в процессе TD-обучения мы "подтягиваем" значение функции ценности того состояния, в котором мы находились на предыдущем шаге, к значению функции ценности того состояния, в котором мы находимся сейчас, а в DQN мы делаем это с помощью нейронной сети, и если использовать одну и ту же сеть для оценки $Q(s', a')$ и $Q(s, a)$, то этот процесс может превратиться в нескончаемую погоню за целью, которую невозможно достичь, поскольку с каждым обновлением весов, приближающим нас к цели, одновременно сама цель будет удаляться от нас (как на рисунке ниже):
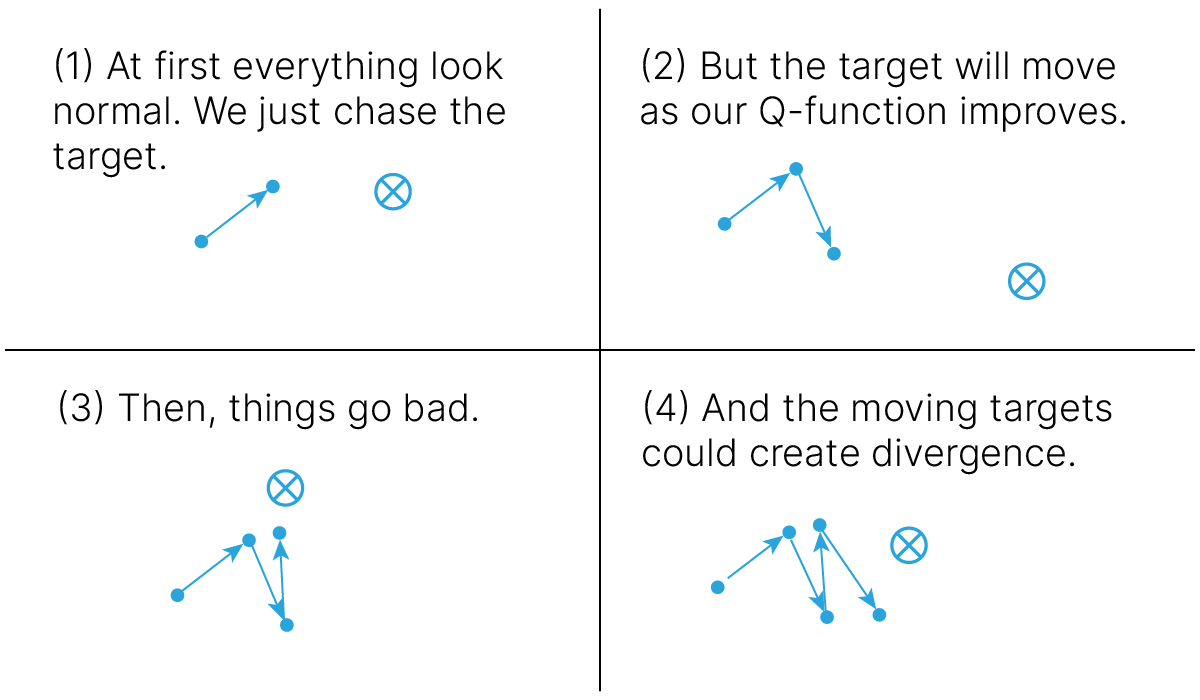
К счастью, эта проблема решаема: нужно сделать так, чтобы сеть обучалась некоторое время аппроксимировать оценку $\max_{a'} Q(s', a')$, полученную без использования обновленных весов Q-сети. Для этого используют целевую сеть (target network) с зафиксированными весами, обновляемыми раз в несколько эпизодов обучения (например, эпох или игровых эпизодов, если обучение происходит после каждого игрового эпизода).
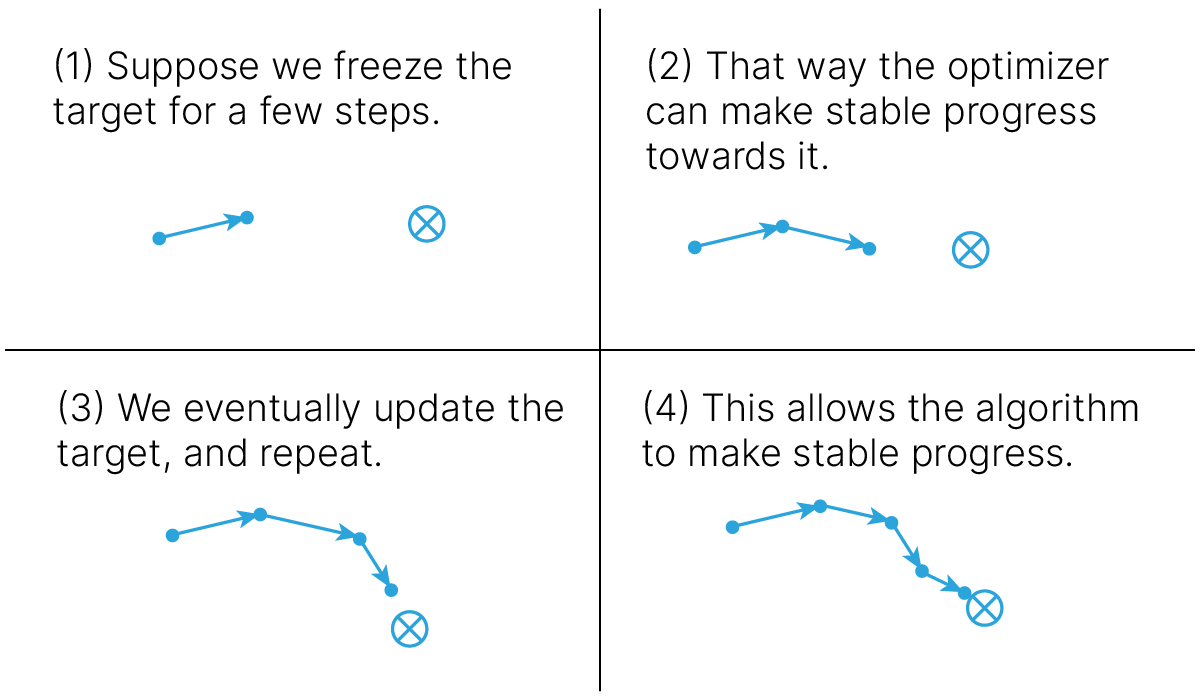
Таким образом, параллельно будут существовать две сети, одна из которых будет отвечать за выбор действия, другая — за целевую функцию, одна из которых будет обучаться с отставанием.
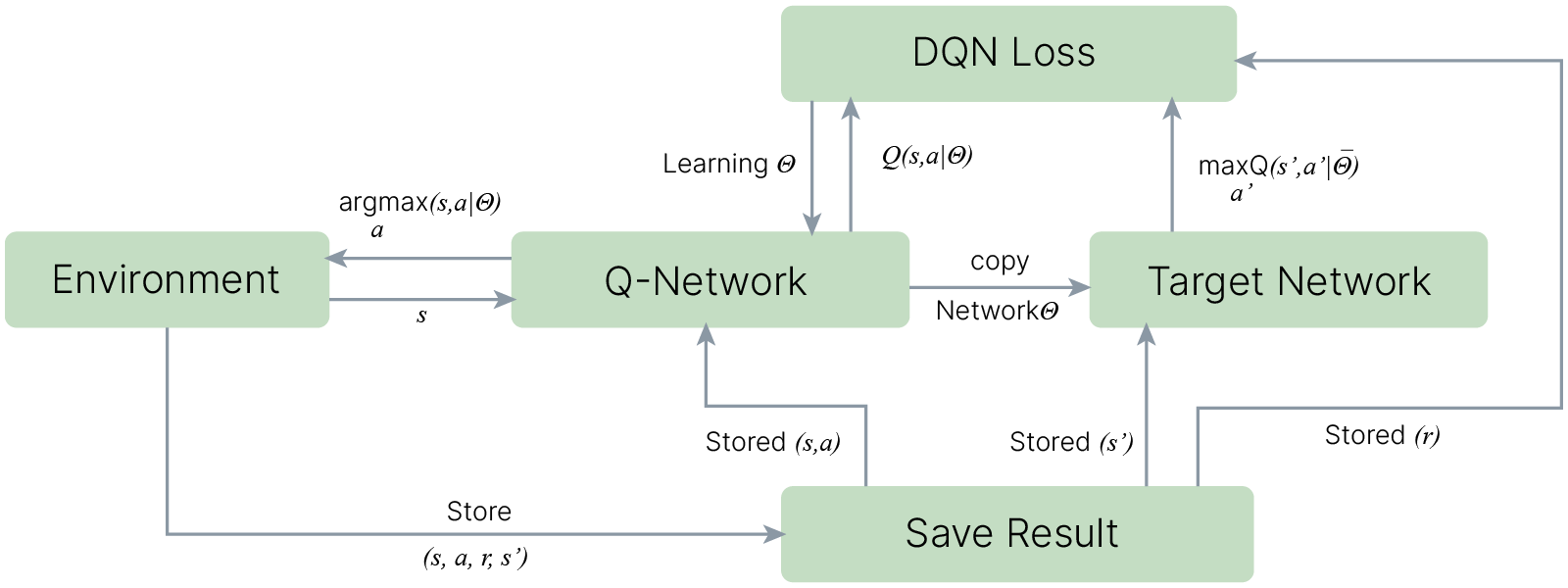
Сеть Deep Q = DQN (Deep Q-Network).
CartPole — перевернутый маятник с центром тяжести над своей точкой поворота. Он нестабилен, но его можно контролировать, перемещая точку поворота под центром масс. Цель состоит в том, чтобы сохранить равновесие, прикладывая соответствующие усилия к точке поворота.
Другой env можно использовать без каких-либо изменений кода. Пространство состояний должно быть единым вектором, действия должны быть дискретными.
CartPole — самый простой. На ее решение должно уйти несколько минут.
Для LunarLander может потребоваться 1–2 часа, чтобы получить 200 баллов (хороший балл) в Colab, и прогресс в обучении не выглядит информативным.
from IPython.display import clear_output
import os
################################################
# For CartPole
################################################
!wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/setup_colab.sh -O- | bash
!wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/week04_approx_rl/atari_wrappers.py
!wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/week04_approx_rl/utils.py
!wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/week04_approx_rl/replay_buffer.py
!wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/master/week04_approx_rl/framebuffer.py
!pip install swig
!pip install gym[box2d]
!touch .setup_complete
# This code creates a virtual display to draw game images on.
# It will have no effect if your machine has a monitor.
if type(os.environ.get("DISPLAY")) is not str or len(os.environ.get("DISPLAY")) == 0:
!bash ../xvfb start
os.environ["DISPLAY"] = ":1"
clear_output()
import gym
ENV_NAME = "CartPole-v1"
def make_env(seed=None):
# some envs are wrapped with a time limit wrapper by default
env = gym.make(ENV_NAME, render_mode="rgb_array", new_step_api=True).unwrapped
if seed is not None:
env.seed(seed)
return env
import matplotlib.pyplot as plt
import numpy as np
from warnings import simplefilter
simplefilter("ignore", category=DeprecationWarning)
env = make_env()
env.reset()
env_img = np.squeeze(env.render())
clear_output()
plt.imshow(env_img)
state_shape, n_actions = env.observation_space.shape, env.action_space.n
Теперь нам нужно построить нейронную сеть, которая может сопоставлять наблюдения с состоянием q-значений.
Модель не должна быть слишком сложной: 1–2 скрытых слоя с < 200 нейронами и активацией ReLU, вероятно, будет достаточно.
Batch Normalization и Dropout могут все испортить, поэтому их не используем.
import torch
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# those who have a GPU but feel unfair to use it can uncomment:
# device = torch.device('cpu')
print(state_shape)
(4,)
from torch import nn
class DQNAgent(nn.Module):
def __init__(self, state_shape, n_actions, epsilon=0):
super().__init__()
self.epsilon = epsilon
self.n_actions = n_actions
self.state_shape = state_shape
# Define your network body here. Please make sure agent is fully contained here
assert len(state_shape) == 1
state_dim = state_shape[0]
# Define NN
##############################################
hidden_size = 150
self._nn = nn.Sequential(
nn.Linear(state_dim, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, n_actions),
nn.ReLU(),
)
##############################################
def forward(self, state_t):
"""
takes agent's observation (tensor), returns qvalues (tensor)
:param state_t: a batch states, shape = [batch_size, *state_dim=4]
"""
# Use your network to compute qvalues for given state
##############################################
qvalues = self._nn(state_t)
##############################################
assert qvalues.requires_grad, "qvalues must be a torch tensor with grad"
assert (
len(qvalues.shape) == 2
and qvalues.shape[0] == state_t.shape[0]
and qvalues.shape[1] == n_actions
)
return qvalues
def get_qvalues(self, states):
"""
like forward, but works on numpy arrays, not tensors
"""
model_device = next(self.parameters()).device
states = torch.tensor(states, device=model_device, dtype=torch.float32)
qvalues = self.forward(states)
return qvalues.data.cpu().numpy()
def sample_actions(self, qvalues):
"""pick actions given qvalues. Uses epsilon-greedy exploration strategy."""
epsilon = self.epsilon
batch_size, n_actions = qvalues.shape
random_actions = np.random.choice(n_actions, size=batch_size)
best_actions = qvalues.argmax(axis=-1)
should_explore = np.random.choice([0, 1], batch_size, p=[1 - epsilon, epsilon])
return np.where(should_explore, random_actions, best_actions)
agent = DQNAgent(state_shape, n_actions, epsilon=0.5).to(device)
def evaluate(env, agent, n_games=1, greedy=False, t_max=10000):
"""Plays n_games full games. If greedy, picks actions as argmax(qvalues). Returns mean reward."""
rewards = []
for _ in range(n_games):
s = env.reset()
reward = 0
for _ in range(t_max):
qvalues = agent.get_qvalues([s])
action = (
qvalues.argmax(axis=-1)[0]
if greedy
else agent.sample_actions(qvalues)[0]
)
s, r, done, _, _ = env.step(action)
reward += r
if done:
break
rewards.append(reward)
return np.mean(rewards)
Интерфейс довольно прост:
exp_replay.add(obs, act, rw, next_obs, done) — сохраняет (s,a,r,s',done) кортеж в буфер?exp_replay.sample(batch_size) — возвращает observations, actions, rewards, next_observations и is_done для batch_size random samples,len(exp_replay) — возвращает количество элементов, хранящихся в replay buffer.from replay_buffer import ReplayBuffer
exp_replay = ReplayBuffer(2000)
target_network = DQNAgent(agent.state_shape, agent.n_actions, epsilon=0.5).to(device)
# This is how you can load weights from agent into target network
target_network.load_state_dict(agent.state_dict())
<All keys matched successfully>
Вычислим ошибку TD Q-learning:
$$ \large L = { 1 \over N} \sum_i [ Q_{\theta}(s,a) - Q_\text{reference}(s,a) ] ^2 $$С Q-reference, определенным как:
$$ \large Q_\text{reference}(s,a) = r(s,a) + \gamma \cdot \max_{a'} Q_\text{target}(s', a'), $$где:
def compute_td_loss(
states,
actions,
rewards,
next_states,
is_done,
agent,
target_network,
gamma=0.99,
check_shapes=False,
device=device,
):
"""Compute td loss using torch operations only. Use the formulae above."""
states = torch.tensor(
states, device=device, dtype=torch.float32
) # shape: [batch_size, *state_shape]
actions = torch.tensor(
actions, device=device, dtype=torch.int64
) # shape: [batch_size]
rewards = torch.tensor(
rewards, device=device, dtype=torch.float32
) # shape: [batch_size]
# shape: [batch_size, *state_shape]
next_states = torch.tensor(next_states, device=device, dtype=torch.float)
is_done = torch.tensor(
is_done.astype("float32"),
device=device,
dtype=torch.float32,
) # shape: [batch_size]
is_not_done = 1 - is_done
# get q-values for all actions in current states
predicted_qvalues = agent(states) # shape: [batch_size, n_actions]
# compute q-values for all actions in next states
# with torch.no_grad():
predicted_next_qvalues = target_network(
next_states
) # shape: [batch_size, n_actions]
# select q-values for chosen actions
predicted_qvalues_for_actions = predicted_qvalues[
range(len(actions)), actions
] # shape: [batch_size]
# compute V*(next_states) using predicted next q-values
##############################################
next_state_values = predicted_next_qvalues.max(axis=-1)[0]
##############################################
assert (
next_state_values.dim() == 1 and next_state_values.shape[0] == states.shape[0]
), "must predict one value per state"
# compute "target q-values" for loss - it's what's inside square parentheses in the above formula.
# at the last state use the simplified formula: Q(s,a) = r(s,a) since s' doesn't exist
# you can multiply next state values by is_not_done to achieve this.
###############################################
target_qvalues_for_actions = rewards + gamma * next_state_values * is_not_done
##############################################
# mean squared error loss to minimize
loss = torch.mean(
(predicted_qvalues_for_actions - target_qvalues_for_actions.detach()) ** 2
)
if check_shapes:
assert (
predicted_next_qvalues.data.dim() == 2
), "make sure you predicted q-values for all actions in next state"
assert (
next_state_values.data.dim() == 1
), "make sure you computed V(s') as maximum over just the actions axis and not all axes"
assert (
target_qvalues_for_actions.data.dim() == 1
), "there's something wrong with target q-values, they must be a vector"
return loss
import random
seed = 42
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
env = make_env()
env.reset(seed=seed)
state_dim = env.observation_space.shape
n_actions = env.action_space.n
state = env.reset()
agent = DQNAgent(state_dim, n_actions, epsilon=1).to(device)
target_network = DQNAgent(state_dim, n_actions, epsilon=1).to(device)
target_network.load_state_dict(agent.state_dict())
<All keys matched successfully>
Один агент для игры, второй для обучения. Периодически веса обученного агента копируются в "игрока".
def play_and_record(initial_state, agent, env, exp_replay, n_steps=1):
"""
Play the game for exactly n_steps, record every (s,a,r,s', done) to replay buffer.
Whenever game ends, add record with done=True and reset the game.
It is guaranteed that env has done=False when passed to this function.
PLEASE DO NOT RESET ENV UNLESS IT IS "DONE"
:returns: return sum of rewards over time and the state in which the env stays
hint: use agent.sample.actions
"""
s = initial_state
sum_rewards = 0
# Play the game for n_steps as per instructions above
for _ in range(n_steps):
qvalues = agent.get_qvalues([s])
action = agent.sample_actions(qvalues)[0]
# action = action.argmax(axis=-1)[0]
state, reward, done, _, _ = env.step(action)
sum_rewards += reward
exp_replay.add(s, action, reward, state, done)
if done:
state = env.reset()
s = state
return sum_rewards, s
import utils
from warnings import simplefilter
simplefilter("ignore", category=UserWarning)
REPLAY_BUFFER_SIZE = 10**4
exp_replay = ReplayBuffer(REPLAY_BUFFER_SIZE)
for i in range(100):
if not utils.is_enough_ram(min_available_gb=0.1):
print(
"""
Less than 100 Mb RAM available.
Make sure the buffer size in not too huge.
Also check, maybe other processes consume RAM heavily.
"""
)
break
play_and_record(state, agent, env, exp_replay, n_steps=10**2)
if len(exp_replay) == REPLAY_BUFFER_SIZE:
break
print(len(exp_replay))
10000
import time
timesteps_per_epoch = 1
batch_size = 32
total_steps = 4 * 10**4
decay_steps = 1 * 10**4
optimizer = torch.optim.Adam(agent.parameters(), lr=1e-4)
init_epsilon = 1
final_epsilon = 0.1
loss_freq = 20
refresh_target_network_freq = 100
eval_freq = 1000
max_grad_norm = 5000
mean_rw_history = []
td_loss_history = []
grad_norm_history = []
initial_state_v_history = []
step = 0
def wait_for_keyboard_interrupt():
try:
while True:
time.sleep(1)
except KeyboardInterrupt:
pass
from tqdm import trange
state = env.reset()
with trange(step, total_steps + 1) as progress_bar:
for step in progress_bar:
if not utils.is_enough_ram():
print("less that 100 Mb RAM available, freezing")
print("make sure everything is ok and use KeyboardInterrupt to continue")
wait_for_keyboard_interrupt()
agent.epsilon = utils.linear_decay(
init_epsilon, final_epsilon, step, decay_steps
)
# play
_, state = play_and_record(state, agent, env, exp_replay, timesteps_per_epoch)
# train
# sample batch_size of data from experience replay
s, a, r, next_s, is_done = exp_replay.sample(batch_size)
# loss = compute TD loss
loss = compute_td_loss(s, a, r, next_s, is_done, agent, target_network)
loss.backward()
grad_norm = nn.utils.clip_grad_norm_(agent.parameters(), max_grad_norm)
optimizer.step()
optimizer.zero_grad()
if step % loss_freq == 0:
td_loss_history.append(loss.data.cpu().item())
grad_norm_history.append(grad_norm.data.cpu().item())
if step % refresh_target_network_freq == 0:
# Load agent weights into target_network
target_network.load_state_dict(agent.state_dict())
if step % eval_freq == 0:
mean_rw_history.append(
evaluate(make_env(seed=step), agent, n_games=3, greedy=True, t_max=1000)
)
initial_state_q_values = agent.get_qvalues([make_env(seed=step).reset()])
initial_state_v_history.append(np.max(initial_state_q_values))
clear_output(True)
print("buffer size = %i, epsilon = %.5f" % (len(exp_replay), agent.epsilon))
plt.figure(figsize=[16, 9])
plt.subplot(2, 2, 1)
plt.title("Mean reward per episode")
plt.plot(mean_rw_history)
plt.grid()
assert not np.isnan(td_loss_history[-1])
plt.subplot(2, 2, 2)
plt.title("TD loss history (smoothened)")
plt.plot(utils.smoothen(td_loss_history))
plt.grid()
plt.subplot(2, 2, 3)
plt.title("Initial state V")
plt.plot(initial_state_v_history)
plt.grid()
plt.subplot(2, 2, 4)
plt.title("Grad norm history (smoothened)")
plt.plot(utils.smoothen(grad_norm_history))
plt.grid()
plt.show()
buffer size = 10000, epsilon = 0.10000
100%|██████████| 40001/40001 [05:35<00:00, 119.07it/s]
final_score = evaluate(make_env(), agent, n_games=30, greedy=True, t_max=1000)
print("final score:", final_score)
if final_score > 300:
print("Well done")
else:
print("not good enough for DQN")
final score: 98.9 not good enough for DQN
Литература
Дополнительно: