Рекуррентные нейронные сети (RNN)
В предыдущих лекциях мы работали с данными фиксированной длины, у которых не было временной связности.
Если это табличные данные, то мы заранее знаем длину вектор-описания объекта, а также размер выхода модели: одно это число или вектор.
Верно это и про изображения — обычно нейронная сеть учится на изображениях определенного разрешения. Да, мы можем сделать нейросеть, которая способна работать с изображением почти любого разрешения, но добиваемся мы этого за счет вставки слоев global pooling, которые приводят признаковое описание, полученное сверточной частью нейросети, к фиксированному размеру.
Однако далеко не все данные фиксированного размера. К примеру, тексты. Возьмем все абзацы из "Войны и Мира". Какие-то будут больше, какие-то меньше. А ещё нам важна последовательность слов и предложений.
Или если на основе абзаца текста нам необходимо сгенерировать его краткое содержание? То, что нужно предсказать, может быть разной длины. Аналогичный вопрос возникает также в случае, если мы хотим по данным о курсе валюты за прошлый год спрогнозировать курс валюты на следующий месяц по дням.
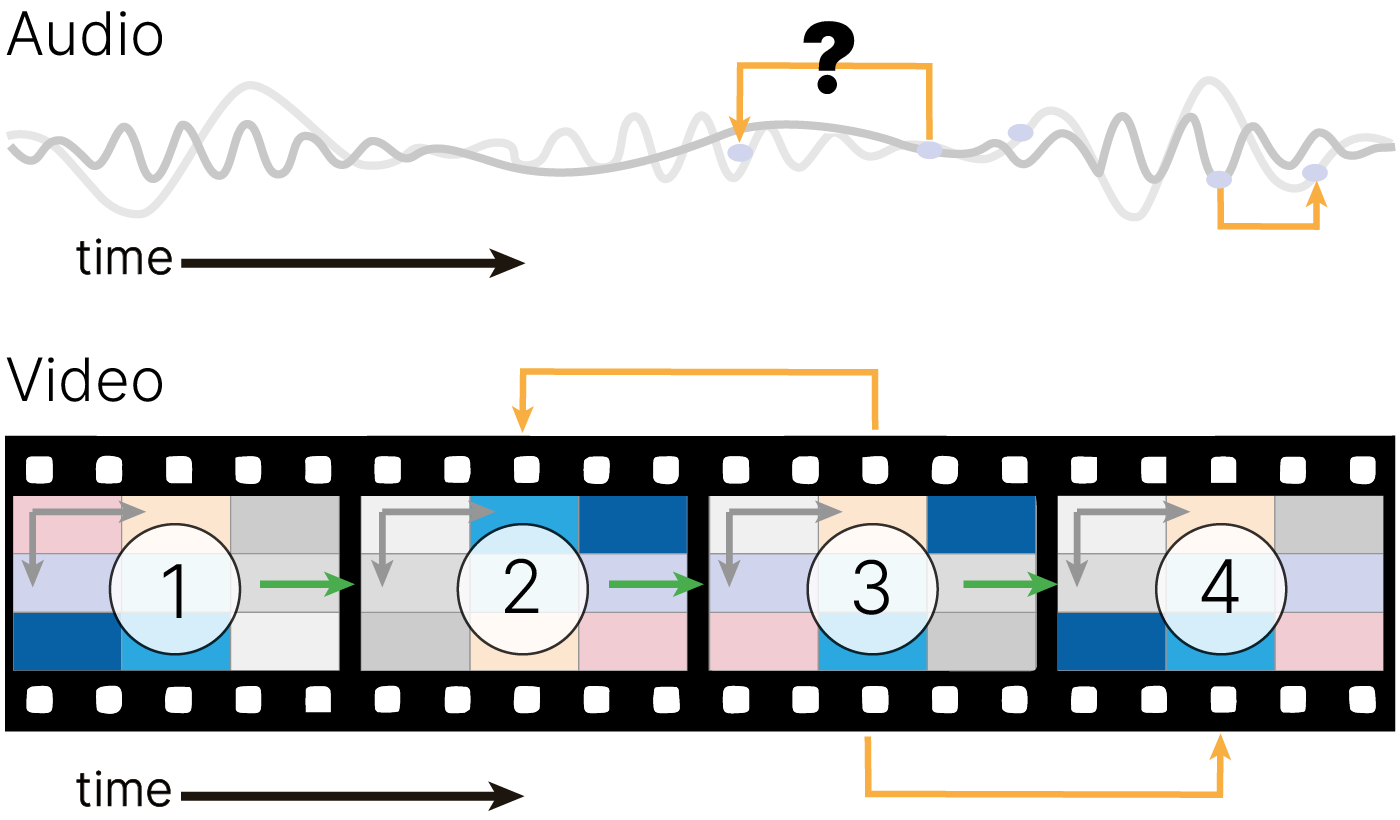
Но, может, справимся уже имеющимися инструментами?
Основные понятия в статистическом анализе временных рядов:
Тренд — компонента, описывающая долгосрочное изменение уровня ряда.
Сезонность — компонента, обозначаемая как $Q$, описывает циклические изменения уровня ряда.
Ошибка (random noise) — непрогнозируемая случайная компонента, описывает нерегулярные изменения в данных, необъяснимые другими компонентами.
$$\large y_i = T_i + Q_i + ϵ_i$$Автокорреляция — статистическая взаимосвязь между последовательностями величин одного ряда. Это один из самых важных коэффициентов в анализе временного ряда. Чтобы посчитать автокорреляцию, используется корреляция между временным рядом и её сдвинутой копией от величины временного сдвига. Сдвиг ряда называется лагом.
Автокорреляционная функция — автокорреляция при разных лагах, помогает находить повторяющиеся участки сигнала. График называется коррелограммой.
Пример
Возьмем датасет Air Passengers 🛠️[doc], который содержит данные о количестве пассажиров за каждый месяц.
import pandas as pd
dataset = pd.read_csv(
"https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/airline-passengers.csv"
)
dataset.head()
| Month | Passengers | |
|---|---|---|
| 0 | 1949-01 | 112 |
| 1 | 1949-02 | 118 |
| 2 | 1949-03 | 132 |
| 3 | 1949-04 | 129 |
| 4 | 1949-05 | 121 |
import matplotlib.pyplot as plt
training_data = dataset.iloc[:, 1:2].values # transform dataframe to numpy.array
# plotting
plt.figure(figsize=(12, 4))
plt.plot(training_data, label="Airline Passangers Data")
plt.title("Number of passengers per month")
plt.ylabel("#passengers")
plt.xlabel("Month")
labels_to_display = [i for i in range(training_data.shape[0]) if i % 12 == 0]
plt.xticks(labels_to_display, dataset["Month"][labels_to_display])
plt.grid()
plt.show()
Сделаем стационарнее
Мы можем видеть четкую сезонность и тенденцию к увеличению значений.
Тенденция и сезонность являются фиксированными компонентами, которые могут быть добавлены к любому нашему прогнозу. Они полезны, но должны быть удалены, чтобы изучить любые другие систематические сигналы, которые могут помочь сделать прогнозы.
Многие методы и модели основаны на предположениях о стационарности ряда, поэтому для проверки стационарности давайте проведем обобщенный тест Дикки-Фуллера 📚[wiki] на наличие единичных корней. Для этого в модуле statsmodels есть функция adfuller().
Стационарным называется ряд, у которго среднее, дисперсия и и ковариация постоянны.
import statsmodels.api as sm
test = sm.tsa.adfuller(training_data)
print("adf: ", test[0])
print("p-value: ", test[1])
print("Critical values: ", test[4])
if test[0] > test[4]["5%"]:
print("The time series is not stationary")
else:
print("The time series is stationary")
adf: 0.8153688792060528
p-value: 0.9918802434376411
Critical values: {'1%': -3.4816817173418295, '5%': -2.8840418343195267, '10%': -2.578770059171598}
The time series is not stationary
Оценим тренд.
# Calculate the trend
trend = dataset["Passengers"].rolling(window=12).mean()
trend.plot(figsize=(12, 2))
plt.xlabel("Month")
plt.ylabel("Trend")
plt.show()
Чтобы убрать сезонность, мы можем взять сезонную разницу, которая приведет к так называемым сезонно скорректированным временным рядам.
Период сезонности составляет один год (12 месяцев). Приведенный ниже код рассчитывает сезонно скорректированный временной ряд.
# Calculate the seasonality
seasonality = dataset["Passengers"] - trend
seasonality.plot(figsize=(12, 2))
plt.xlabel("Month")
plt.ylabel("Seasonality")
plt.show()
test = sm.tsa.adfuller(seasonality.dropna())
print("adf: ", test[0])
print("p-value: ", test[1])
print("Critical values: ", test[4])
if test[0] > test[4]["5%"]:
print("The time series is not stationary")
else:
print("The time series is stationary")
adf: -3.1649681299551475
p-value: 0.02210413947387869
Critical values: {'1%': -3.4865346059036564, '5%': -2.8861509858476264, '10%': -2.579896092790057}
The time series is stationary
Авторегрессионная модель (Autoregression method (AR))
Линейная модель, в которой прогнозированная величина является суммой прошлых значений, умноженных на числовой множитель.
$$\large X_t = C + ϕ_{t-1}X_{t-1}+ϕ_{t-2}X_{t-2}...+ ϵ_t$$Метод скользящего среднего (Moving average method (MA))
Расчет точек путем создания ряда взвешенных средних значений различных подмножеств полного набора данных:
$$\large \text{WWMA}_t= \frac {w_{t-1}p_{t-1} + w_{t-2}p_{t-2} ... w_{t-n+1}p_{t-n+1}} {w_{t-1} + w_{t-2} ... w_{n}} = \frac {\sum ^ {n-1} _{i= 0} w_{t-i}p_{t-i}}{\sum ^ {n-1} _{i= 0}w_{t-i}} $$Скользящее среднее часто применяется для анализа временных рядов акций.
ARMA
Для стационарных процессов используется модель ARMA(p,q), которая в общем виде выглядит следующим образом:
$$\large X_t = ϕ_{t-1}X_{t-1} + ⋯ + ϕ_{t-p}X_{t-p} + ε_t + w_{t-1}p_{t-1} + ⋯ + w_{t-q}p_{t-q},$$где $ϕ_t$ — коэффициенты авторегрессионной части модели, $ε_t$ — значения ошибки (полагаются независимыми одинаково распределёнными случайными величинами из нормального распределения с нулевым средним), $w_j$ — коэффициенты скользящего среднего.
Модель предполагает, что временной ряд содержит две составляющие: авторегресионную и скользящее среднее, которые в модели обозначены $p$ и $q$:
ARIMA
Если ряд после взятия d последовательных разностей сводится к стационарному, то для для прогнозирования можно применить комбинированную модель авторегрессии и скользящего среднего, обозначаемую как ARIMA(p,d,q):
$$ \large (Δ^dX_t) = \sum ^p _{t=1} ϕ_t(Δ^dX_{t-1}) + ε_t + \sum ^q _{j=1} w_j(Δ^d ε_{t-j}) $$Модель предполагает, что временной ряд содержит три составляющие: авторегресионную, скользящее среднее и интегрированную, которые в модели обозначены $p, d$ и $q$. Т.е. добавилось:
Разновидности: Seasonable ARIMA, ARIMAX и пр.
Параметры
Автокорреляционная функция ACF поможет определить $q$, т. к. по ее коррелограмме можно определить количество автокорреляционных коэффициентов, сильно отличных от $0$, в модели MA.
Частично автокорреляционная функция PACF поможет определить $p$, т. к. по ее коррелограмме можно определить максимальный номер коэффициента, сильно отличного от $0$, в модели AR.
# first-order difference
dfOrigin = dataset["Passengers"]
df1 = dfOrigin.diff(1).dropna()
# second-order difference
df2 = df1.diff(1).dropna()
# third-order difference
df3 = df2.diff(1).dropna()
# plot three curves and check the stationary
fig, (ax1, ax2, ax3) = plt.subplots(nrows=3, ncols=1, sharex=True)
ax1.plot(df1)
ax1.set_title("first order")
ax2.plot(df2)
ax2.set_title("second order")
ax3.plot(df3)
ax3.set_title("third order")
plt.show()
def check_stationary(ts_data):
df_test = sm.tsa.adfuller(ts_data)
output = pd.Series(
df_test[0:4], index=["Test statistic", "p-value", "used_lag", "NOBS"]
)
print(output)
check_stationary(df1)
check_stationary(df2)
check_stationary(df3)
Test statistic -2.829267 p-value 0.054213 used_lag 12.000000 NOBS 130.000000 dtype: float64 Test statistic -1.638423e+01 p-value 2.732892e-29 used_lag 1.100000e+01 NOBS 1.300000e+02 dtype: float64 Test statistic -9.434675e+00 p-value 5.079967e-16 used_lag 1.400000e+01 NOBS 1.260000e+02 dtype: float64
Коррелограмма
Показывает корреляцию каждого отсроченного наблюдения и позволяет оценить ее статистическую значимость.
fig = plt.figure(figsize=(10, 6))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(dataset["Passengers"].values.squeeze(), lags=20, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(dataset["Passengers"], lags=20, ax=ax2)
plt.show()
На графике показаны значения запаздывания по оси $X$ и корреляции по оси $Y$ между $-1$ и $1$ для отрицательно и положительно коррелированных лагов соответственно. Точки над синей областью указывают на статистическую значимость. Это зона достоверности, по умолчанию на $0.05$.
from statsmodels.tsa.seasonal import seasonal_decompose
data = dataset.iloc[:, 1:2]
result = seasonal_decompose(
x=data, model="multiplicative", extrapolate_trend="freq", period=12
)
fig = result.plot()
plt.show()
Воспользуемся библиотечной версией ARIMA. Разобьём данные и поставим параметры. Обучим модель.
dataset["Month"] = pd.to_datetime(dataset["Month"])
dataset = dataset.set_index(["Month"])
dataset.index = pd.DatetimeIndex(dataset.index.values, freq=dataset.index.inferred_freq)
train_data, test_data = (
dataset[0 : int(len(data) * 0.9)],
dataset[int(len(data) * 0.9) :],
)
from statsmodels.tsa.arima.model import ARIMA
model = ARIMA(
train_data, order=(12, 2, 13), freq=dataset.index.inferred_freq
) # (p,d,q)
from warnings import simplefilter
simplefilter("ignore")
model_fit = model.fit()
start_data = train_data.index[-1] + pd.DateOffset(months=1)
end_data = test_data.index[-1] + pd.DateOffset(months=len(test_data))
predictions = model_fit.predict(start=start_data, end=end_data)
Визуализируем:
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 4))
plt.plot(train_data["Passengers"], color="green", label="Train")
plt.plot(test_data["Passengers"], color="red", label="Real")
plt.plot(predictions, color="blue", label="Predicted")
plt.title("ARIMA with optimal parameters")
plt.legend()
plt.show()
Оценим метрики.
import math
from sklearn.metrics import mean_squared_error, mean_absolute_error
# report performance
mse = mean_squared_error(test_data["Passengers"], predictions[:15])
print("MSE: " + str(mse))
mae = mean_absolute_error(test_data["Passengers"], predictions[:15])
print("MAE: " + str(mae))
rmse = math.sqrt(mean_squared_error(test_data["Passengers"], predictions[:15]))
print("RMSE: " + str(rmse))
MSE: 264.3382033445668 MAE: 13.372375060851368 RMSE: 16.258480966700635
Предсказание есть, однако можно ли его как-то улучшить? Да так, чтобы без ручного анализа и подбора параметров?
!pip install -q pmdarima
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 2.1/2.1 MB 32.4 MB/s eta 0:00:00
from pmdarima.arima import auto_arima
stepwise_model = auto_arima(
train_data,
start_p=1,
start_q=1,
max_p=3,
max_q=3,
m=12,
start_P=0,
seasonal=True,
d=1,
D=1,
trace=True,
error_action="ignore",
suppress_warnings=True,
stepwise=True,
)
print(stepwise_model.aic())
Performing stepwise search to minimize aic ARIMA(1,1,1)(0,1,1)[12] : AIC=879.138, Time=0.46 sec ARIMA(0,1,0)(0,1,0)[12] : AIC=881.901, Time=0.06 sec ARIMA(1,1,0)(1,1,0)[12] : AIC=877.920, Time=0.27 sec ARIMA(0,1,1)(0,1,1)[12] : AIC=878.938, Time=0.30 sec ARIMA(1,1,0)(0,1,0)[12] : AIC=876.775, Time=0.10 sec ARIMA(1,1,0)(0,1,1)[12] : AIC=878.101, Time=0.29 sec ARIMA(1,1,0)(1,1,1)[12] : AIC=inf, Time=1.13 sec ARIMA(2,1,0)(0,1,0)[12] : AIC=877.993, Time=0.07 sec ARIMA(1,1,1)(0,1,0)[12] : AIC=877.677, Time=0.08 sec ARIMA(0,1,1)(0,1,0)[12] : AIC=877.710, Time=0.06 sec ARIMA(2,1,1)(0,1,0)[12] : AIC=879.650, Time=0.20 sec ARIMA(1,1,0)(0,1,0)[12] intercept : AIC=878.414, Time=0.10 sec Best model: ARIMA(1,1,0)(0,1,0)[12] Total fit time: 3.135 seconds 876.7750530228392
stepwise_model.fit(train_data)
ARIMA(1,1,0)(0,1,0)[12]In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
ARIMA(1,1,0)(0,1,0)[12]
future_forecast = stepwise_model.predict(start=start_data, n_periods=(len(predictions)))
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 4))
plt.plot(train_data["Passengers"], color="green", label="Train")
plt.plot(test_data["Passengers"], color="red", label="Real")
plt.plot(future_forecast, color="blue", label="Predicted")
plt.title("ARIMA with optimal parameters")
plt.xlabel("Time")
plt.ylabel("Passengers")
plt.legend()
plt.grid(True)
plt.show()
mse = mean_squared_error(test_data["Passengers"], future_forecast[: len(test_data)])
print("MSE: " + str(mse))
mae = mean_absolute_error(test_data["Passengers"], future_forecast[: len(test_data)])
print("MAE: " + str(mae))
rmse = math.sqrt(
mean_squared_error(test_data["Passengers"], future_forecast[: len(test_data)])
)
print("RMSE: " + str(rmse))
MSE: 328.92348797154153 MAE: 13.990150688148209 RMSE: 18.136247902241013
Получилось примерно также, но при этом гораздо быстрее.
Обратите внимание на разбиение временного ряда на train-val-test.
Если мы поделим ряд на отрезки, точки склейки будут легко предсказываться либо предыдущим, либо средним значением по отрезку. Нужно предсказывать крупные отрезки ряда. И помнить о том, что перемешивать данные нельзя — есть "прошлое" и "будущее".
Анализируемые данные могут быть многомерными. И признаками могут быть категориальные переменные, изображения и др. Усложнение задач приводит к невозможности их решения с помощью классических методов (или сложность сведения к классической формулировке непомерно высока). Зачастую в таких случая могут помочь, например, рекуррентные нейронные сети.

До бурного развития архитектуры Трансформер, о которой будет рассказано в соответствующей лекции, рекуррентные сети применялись в широком перечне задач, от распознавания речи до генерации подписей к изображениям. Общее для задач — возможность сохранять информацию, сформированную при обработке одной части объекта (токена), и использовать ее при анализе других частей.
В настоящий момент рекуррентные сети держат первенство в обработке временных рядов, а также являются частью гибридных моделей.
Хотя Трансформеры, как правило, превосходят RNN с точки зрения точности, важно помнить о необходимых вычислительных ресурсах. По своей сути большое количество параметров и слоев в Трансформерах приводит к критическому увеличению объема необходимой памяти и вычислительных требований по сравнению с RNN.
Основная идея, на которой основаны рекуррентные нейронные сети (RNN), состоит в следующем: взять всю последовательность и пропустить через одну и ту же нейросеть. Но при этом сама нейросеть кроме следующего элемента последовательности (например, слова в тексте) будет принимать еще один параметр — некий $h$, который в начале будет, например, вектором из нулей, а далее — значением, которое выдает сама нейросеть после обработки очередного элемента последовательности (токена).
Также далее мы будем использовать понятие нулевого токена — токена, который символизирует заплатку и не несёт никакого смысла, но который иногда нужно передать модели, например, как сигнал начала работы.
В сети появляется новая сущность — hidden state ($h$) — вектор, хранящий состояние, учитывающее и локальный, и глобальный контекст.
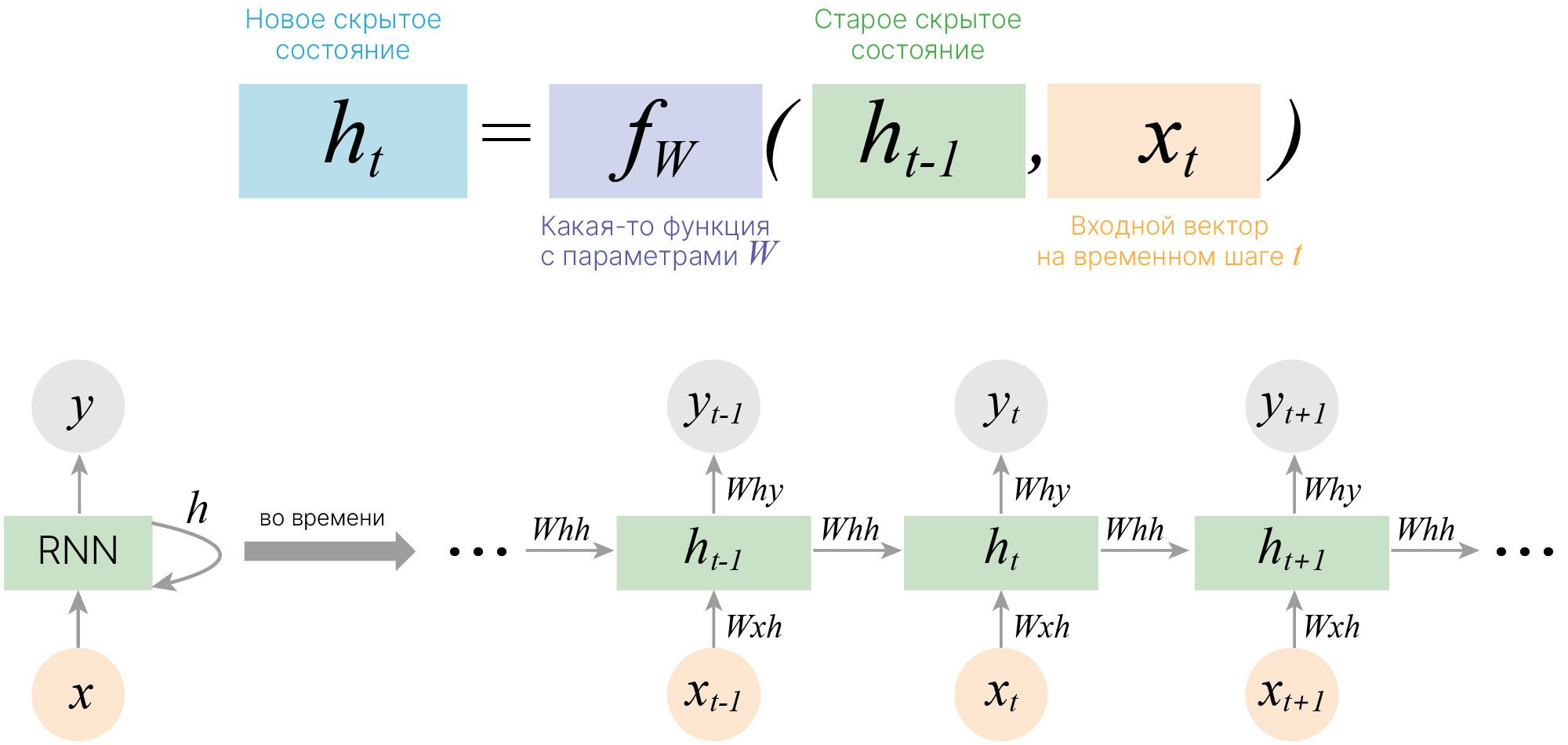
Рассмотрим работу рекуррентной нейронной сети:
На вход поступает некоторая последовательность $x = \{x_1,...x_t,...,x_n\}$, где $x_i$ — вектор фиксированной размерности. В ряде случаев этот вектор имеет размерность $1$.
Для каждого поступившего $x_t$ формируем скрытое состояние $h_t$, которое является функцией от предыдущего состояния $h_{t-1}$ и текущего элемента последовательности $x_t$: $$\large h_t = f_W(h_{t-1}, x_t),$$ где $W$ — это обучаемые параметры (веса).
На основании рассчитанного скрытого состояния, учитывающего предыдущие значения $x_i$, формируется выходная последовательность $y = \{y_1,...y_t,...,y_k\}$. Для формирования предсказания $y_t$ в текущий момент времени в модель могут быть добавлены полносвязные слои, принимающие на вход текущее скрытое состояние $h_t$.
Простейшая RNN. Мы можем обрабатывать последовательность элементов вектора $x$ за счет применения рекуррентной формулы на каждом шаге:
$\large h_t = f_W(h_{t-1}, x_t),$
$\large \quad \quad \quad \color{grey}{\downarrow \text{(также может добавляться bias)}}$
$\large h_t = \tanh(W_{hh}h_{t-1} + W_{xh}x_t).$
$\large y_t = W_{hy}h_t.$
Отличие от слоев, с которыми мы уже сталкивались, состоит в том, что на выходе мы получаем два объекта — $y_t$ и $h_t$:
$y_t$ — предсказание в текущий момент времени, например, метка класса,
$h_t$ — контекст, в котором предсказание было сделано. Он может использоваться для дальнейших предсказаний.
В PyTorch для вычисления $h_t$ используется модуль torch.nn.RNNCell 🛠️[doc].
$y_t$ в нем не вычисляется: предполагается, что для его получения в модель должен быть добавлен дополнительный линейный слой.
input_size — размер элемента последовательности.
В отличие от сверточных слоёв, это всегда вектор, а не тензор, поэтому input_size — скаляр.
hidden_size — тоже скаляр. Он задает размер скрытого состояния, которое тоже является вектором. Фактически это количество нейронов в слое.
import torch
torch.manual_seed(42)
rnn_cell = torch.nn.RNNCell(input_size=3, hidden_size=2)
dummy_sequence = torch.randn((1, 3)) # batch, input_size
h = rnn_cell(dummy_sequence)
print("Inital shape:".ljust(17), f"{dummy_sequence.shape}")
print("Resulting shape:".ljust(17), f"{h.shape}") # hidden state
Inital shape: torch.Size([1, 3]) Resulting shape: torch.Size([1, 2])
Внутри происходит примерно то, что описано в коде ниже.
Для понятности в данном примере опущена батчевая обработка. Также для того, чтобы подобный код корректно заработал, необходимо обернуть веса ✏️[blog] в torch.nn.Parameter для регистрации параметров в модели.
Начальное значение может быть инициализировано нулями, но лучше инициализировать случайными значениями.
from torch import nn
# Simple RNNcell without a bias and batch support
class SimplifiedRNNCell(nn.Module):
def __init__(self, input_size, hidden_size):
super().__init__()
# Init weight matrix, for simplicity omit bias
self.W_hx = (
torch.randn(input_size, hidden_size) * 0.0001
) # hidden_size == number of neurons
self.W_hh = (
torch.randn(hidden_size, hidden_size) * 0.0001
) # naive initialization
self.h0 = torch.zeros((hidden_size)) # Initial hidden state
def forward(self, x, h=None): # Without a batch dimension
if h is None:
h = self.h0
h = torch.tanh(torch.matmul(self.W_hx.T, x) + torch.matmul(self.W_hh.T, h))
return h
simple_rnn_cell = SimplifiedRNNCell(input_size=3, hidden_size=2)
h = simple_rnn_cell(dummy_sequence[0]) # No batch
print(f"Out = h\n{h.shape} \n{h}")
Out = h torch.Size([2]) tensor([-3.6047e-05, -7.6246e-05])
Однако в последовательности всегда несколько элементов. И надо применить алгоритм к каждому.
Поэтому torch.nn.RNNCell напрямую не используется. Для него есть обертка — torch.nn.RNN 🛠️[doc], которая обеспечивает последовательный вызов RNNCell для всех элементов последовательности.
Формат данных для RNN: длина последовательности, батч, размер объекта.
rnn = torch.nn.RNN(input_size=3, hidden_size=2, batch_first=False) # batch_first = True
dummy_batched_seq = torch.randn((2, 1, 3)) # seq_len, batch, input_size
out, h = rnn(dummy_batched_seq)
print("Inital shape:".ljust(20), f"{dummy_batched_seq.shape}")
print("Resulting shape:".ljust(20), f"{out.shape}")
print("Hidden state shape:".ljust(20), f"{h.shape}")
Inital shape: torch.Size([2, 1, 3]) Resulting shape: torch.Size([2, 1, 2]) Hidden state shape: torch.Size([1, 1, 2])
Внутри происходит примерно следующее:
import numpy as np
# Simple RNN without batching
class SimplifiedRNNLayer(nn.Module):
def __init__(self, input_size, hidden_size):
super().__init__()
self.rnn_cell = SimplifiedRNNCell(input_size, hidden_size)
# Without a batch dimension x have shape seq_len * input_size
def forward(self, x, h=None):
all_h = []
for i in range(x.shape[0]): # iterating over timestamps
h = self.rnn_cell(torch.Tensor(x[i]), h)
all_h.append(h)
return np.stack(all_h), h
simple_rnn = SimplifiedRNNLayer(input_size=4, hidden_size=2)
sequence = np.array(
[[0, 1, 2, 0], [3, 4, 5, 0]]
) # batch with one sequence of two elements
out, h = simple_rnn(sequence)
print("Inital shape:".ljust(20), f"{sequence.shape}")
print("Resulting shape:".ljust(20), f"{out.shape}")
print("Hidden state shape:".ljust(20), f"{h.shape}")
Inital shape: (2, 4) Resulting shape: (2, 2) Hidden state shape: torch.Size([2])
Давайте разберемся.
Если у нас есть две последовательности:
Чтобы обработать элемент "3", нам нужен hidden state, вычисленный по "1".
То же самое для "4" — нужно обработать "0". Таким образом, по горизонтальной оси мы не можем распараллелить вычисления, придётся делать это по вертикальной. Мы можем параллельно обработать первые элементы первой и второй последовательностей.
К данным добавляется еще одно измерение — размер последовательности. Batch из 5 последовательностей по 6 объектов (размер объекта 3) в каждой будет выглядеть так (время идёт первой размерностью, поэтому поэлементно идём "сверху вниз"):
Внутри RNN-модуля элементы последовательности обрабатываются последовательно:
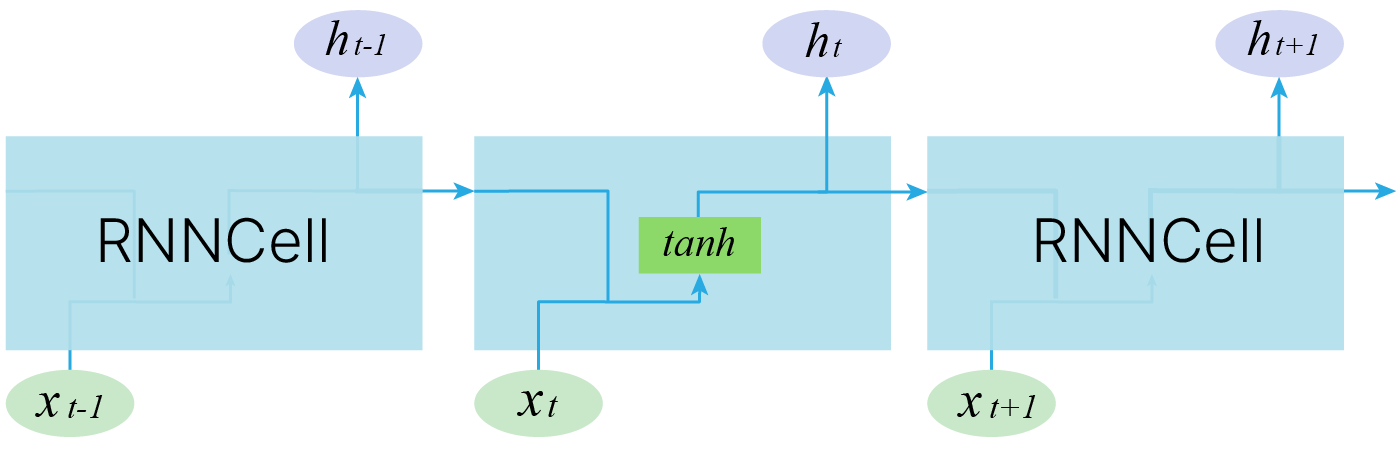
Веса при этом используются одни и те же.
dummy_seq = torch.randn((2, 1, 3)) # seq_len, batch, input_size
print("RNNCell")
rnn_cell = torch.nn.RNNCell(3, 2)
print("Parameter".ljust(10), "Shape")
for t, p in rnn_cell.named_parameters():
print(t.ljust(10), p.shape)
cell_out = rnn_cell(dummy_seq[0, :, :]) # take first element from sequence
print()
print("Result shape =".ljust(20), cell_out.shape)
print("Hidden state shape =".ljust(20), cell_out.shape) # one hidden state
print("----------------------------------------")
print("RNN")
rnn = torch.nn.RNN(3, 2)
print("Parameter".ljust(15), "Shape")
for t, p in rnn.named_parameters():
print(t.ljust(15), p.shape)
out, h = rnn(dummy_seq)
print()
print("Result shape =".ljust(20), out.shape) # h for all timestamps element
print("Hidden state shape =".ljust(20), cell_out.shape) # h for last element
RNNCell Parameter Shape weight_ih torch.Size([2, 3]) weight_hh torch.Size([2, 2]) bias_ih torch.Size([2]) bias_hh torch.Size([2]) Result shape = torch.Size([1, 2]) Hidden state shape = torch.Size([1, 2]) ---------------------------------------- RNN Parameter Shape weight_ih_l0 torch.Size([2, 3]) weight_hh_l0 torch.Size([2, 2]) bias_ih_l0 torch.Size([2]) bias_hh_l0 torch.Size([2]) Result shape = torch.Size([2, 1, 2]) Hidden state shape = torch.Size([1, 2])
Давайте обратимся к PyTorch 🛠️[doc] и посмотрим, какие параметры есть у модуля RNN.
RNN блоки можно объединять в слои, накладывая их друг на друга. Для этой операции в torch.nn.RNN есть аргумент num_layers, с помощью которого можно указать количество слоёв.
В представленной архитектуре нижний слой (а это всё ещё одна RNN-ячейка) обрабатывает букву h, передаёт свой hidden state в саму себя (направо, h[0]) и обрабатывает е и т.д. Кроме того, эта же ячейка передаёт своё состояние на вторую RNN-ячейку (наверх, h[1]), которая уже обрабатывает результат работы первой ячейки.
На практике такая схема может приводить к взрыву или затуханию градиента, причём при проходе как по горизонтали, так и по вертикали. Об этом ниже.

Параметр num_layers задаёт количество RNN-ячеек.
dummy_input = torch.randn((2, 1, 3)) # seq_len, batch, input_size
rnn = torch.nn.RNN(3, 2, num_layers=3)
# Weights matrix sizes not changed!
for t, p in rnn.named_parameters():
print(t, p.shape)
out, h = rnn(dummy_input)
print()
print("Out:\n", out.shape) # Hidden states for all elements from top layer
print("h:\n", h.shape) # Hidden states for last element for all layers
weight_ih_l0 torch.Size([2, 3]) weight_hh_l0 torch.Size([2, 2]) bias_ih_l0 torch.Size([2]) bias_hh_l0 torch.Size([2]) weight_ih_l1 torch.Size([2, 2]) weight_hh_l1 torch.Size([2, 2]) bias_ih_l1 torch.Size([2]) bias_hh_l1 torch.Size([2]) weight_ih_l2 torch.Size([2, 2]) weight_hh_l2 torch.Size([2, 2]) bias_ih_l2 torch.Size([2]) bias_hh_l2 torch.Size([2]) Out: torch.Size([2, 1, 2]) h: torch.Size([3, 1, 2])
Что общего у прогнозирования потребления электроэнергии домохозяйствами, оценки трафика на дорогах в определенные периоды, прогнозировании паводков и прогнозировании цены, по которой акции будут торговаться на фондовой бирже?
Все они попадают под понятие данных временных рядов! Вы не можете точно предсказать любой из этих результатов без компонента «время». И по мере того, как в мире вокруг нас генерируется все больше и больше данных, прогнозирование временных рядов становится все более важной областью применения методов ML и DL.
Снова будем использовать датасет Air Passengers 🛠️[doc]:
import pandas as pd
dataset = pd.read_csv(
"https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/airline-passengers.csv"
)
training_data = dataset.iloc[:, 1:2].values # transform dataframe to numpy.array
# Min-Max normalization
td_min = training_data.min()
td_max = training_data.max()
print("Initial statistics:")
print("Minimum value:", repr(td_min).rjust(5))
print("Maximum value:", repr(td_max).rjust(5))
training_data = (training_data - td_min) / (td_max - td_min)
print("\nResulting statistics:")
print("Minimum value:", repr(training_data.min()).rjust(5))
print("Maximum value:", repr(training_data.max()).rjust(5))
Initial statistics: Minimum value: 104 Maximum value: 622 Resulting statistics: Minimum value: 0.0 Maximum value: 1.0
Поскольку мы хотим научиться предсказывать следующие значение на основе предыдущих, нам нужно подготовить данные соответствующим образом.
Разобьем весь массив данных на фрагменты вида
$x \to y$,
где $x$ — это подпоследовательность, например, записи с 1-й по 8-ю, а $y$ — это значение из 9-й записи, то самое, которое мы хотим предсказать.
import torch
import numpy as np
def sliding_windows(data, seq_length):
x = []
y = []
for i in range(len(data) - seq_length):
_x = data[i : (i + seq_length)] # picking several sequential observations
_y = data[i + seq_length] # picking the subsequent observation
x.append(_x)
y.append(_y)
return torch.Tensor(np.array(x)), torch.Tensor(np.array(y))
# set length of the ensemble; accuracy of the predictions and
# speed perfomance almost always depend on it size
seq_length = 8 # compare 2 and 32
x, y = sliding_windows(training_data, seq_length)
print("Example of the obtained data:\n")
print("Data corresponding to the first x:")
print(x[0])
print("Data corresponding to the first y:")
print(y[0])
Example of the obtained data:
Data corresponding to the first x:
tensor([[0.0154],
[0.0270],
[0.0541],
[0.0483],
[0.0328],
[0.0598],
[0.0849],
[0.0849]])
Data corresponding to the first y:
tensor([0.0618])
Благодаря такому подходу мы можем работать с RNN моделью так же, как работали со сверточными моделями, подавая на вход такую подпоследовательность + результат.
Важный момент. Нельзя допустить утечки в данных. Что будет, если не отступить на длину seq_length?
train_size = int(len(y) * 0.8)
x_train = x[:train_size]
y_train = y[:train_size]
x_test = x[train_size + seq_length :]
y_test = y[train_size + seq_length :]
print("Train data:")
print("x shape:", x_train.shape)
print("y shape:", y_train.shape)
print("\nTest data:")
print("x shape:", x_test.shape)
print("y shape:", y_test.shape)
Train data: x shape: torch.Size([108, 8, 1]) y shape: torch.Size([108, 1]) Test data: x shape: torch.Size([20, 8, 1]) y shape: torch.Size([20, 1])
Обратите внимание на параметр batch_first. Он позволяет записывать данные в привычном формате.
import torch.nn as nn
class AirTrafficPredictor(nn.Module):
def __init__(self, input_size, hidden_size):
# hidden_size == number of neurons
super().__init__()
self.rnn = nn.RNN(
input_size=input_size, hidden_size=hidden_size, batch_first=True
)
self.fc = nn.Linear(hidden_size, 1) # Predict only one value
def forward(self, x):
# print("x: ",x.shape) # 108 x 8 x 1 : [batch_size, seq_len, input_size]
out, h = self.rnn(x)
# print("out: ", out.shape) # 108 x 8 x 4 : [batch_size, seq_len, hidden_size] Useless!
# print("h : ", h.shape) # 1 x 108 x 4 [ num_layers, batch_size, hidden_size]
y = self.fc(h)
# print("y",y.shape) # 1 x 108 x 1
return y, h
Благодаря подготовке данных процесс обучения не будет отличаться от того, что мы использовали на прошедших занятиях.
В силу того, что датасет маленький и все данные поместились в один batch, итерирования по batch-ам в явном виде здесь не происходит.
def time_series_train(model, num_epochs=2000, learning_rate=0.01):
criterion = torch.nn.MSELoss() # mean-squared error for regression
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
# Train the model
for epoch in range(num_epochs):
y_pred, h = model(x_train) # we don't use h there, but we can!
optimizer.zero_grad()
# obtain the loss
loss = criterion(y_pred[0], y_train) # for shape compatibility
loss.backward()
optimizer.step()
if epoch % 100 == 0:
print(f"Epoch: {epoch},".ljust(15), "loss: %1.5f" % (loss.item()))
print("Simple RNN training process with MSE loss:")
input_size = 1
hidden_size = 8
rnn = AirTrafficPredictor(input_size, hidden_size)
time_series_train(rnn)
Simple RNN training process with MSE loss: Epoch: 0, loss: 0.01983 Epoch: 100, loss: 0.00258 Epoch: 200, loss: 0.00223 Epoch: 300, loss: 0.00208 Epoch: 400, loss: 0.00205 Epoch: 500, loss: 0.00204 Epoch: 600, loss: 0.00202 Epoch: 700, loss: 0.00211 Epoch: 800, loss: 0.00196 Epoch: 900, loss: 0.00189 Epoch: 1000, loss: 0.00181 Epoch: 1100, loss: 0.00170 Epoch: 1200, loss: 0.00150 Epoch: 1300, loss: 0.00128 Epoch: 1400, loss: 0.00103 Epoch: 1500, loss: 0.00095 Epoch: 1600, loss: 0.00092 Epoch: 1700, loss: 0.00091 Epoch: 1800, loss: 0.00089 Epoch: 1900, loss: 0.00087
import matplotlib.pyplot as plt
def time_series_plot(train_predict):
data_predict = train_predict.data
y_data_plot = y.data
# Denormalize
data_predict = data_predict[0] * (td_max - td_min) + td_min
y_data_plot = y_data_plot * (td_max - td_min) + td_min
# Plotting
plt.figure(figsize=(12, 4))
plt.axvline(x=train_size + seq_length, c="r", linestyle="--")
# shifting the curve as first y-value not correspond first value overall
plt.plot(np.arange(y_data_plot.shape[0]), y_data_plot)
plt.plot(np.arange(y_data_plot.shape[0]), data_predict)
plt.title("Number of passengers per month")
plt.ylabel("#passengers")
plt.xlabel("Month")
# plt.xticks(labels_to_display, dataset["Month"][labels_to_display])
plt.legend(["Train/Test separation", "Real", "Predicted"])
plt.grid(axis="x")
plt.show()
rnn.eval()
train_predict, h = rnn(x)
time_series_plot(train_predict)
Видим, что модель в принципе справляется с задачей.
Вот только сейчас мы допустили несколько типичных ошибок. Как нужно:
Верную процедуру мы посмотрим в примере ниже, в разделе LSTM, где будем работать с предсказанием синусоид.
Теоретически, можно было бы сразу пропустить все данные через сеть и затем вычислить градиент, однако возникнут следующие проблемы:
Допустим, у нас есть длинная последовательность. Если мы сразу предсказываем, то в каждый момент времени нужно распространить Loss. И все ячейки нужно обновить во время backpropogation. Все градиенты нужно посчитать. Возникают проблемы, связанные с нехваткой памяти.
Есть специальные тесты для проверки, контекст какой длины использует RNN при предсказании. Если мы делаем предсказание только в последней ячейке, может оказаться, что используется, скажем, информация только о последних 10 словах предложения.
Функция активации Tanh постепенно затирает контекст.

Затухающий/взрывающийся градиент (Vanishing/exploding gradient) — явления затухающего и взрывающегося градиента часто встречаются в контексте RNN. И при большой длине последовательности это становится критичным. Причина в том, что зависимость величины градиента от числа слоёв экспоненциальная, поскольку веса умножаются многократно.
$dL ∝ (W)^N$.
$W > 1$ => взрыв
$W < 1$ => затухание

Один из путей решения проблемы — градиентное отсечение (Gradient clipping) — метод, который ограничивает максимально допустимое значение градиента, позволяя избежать градиентного взрыва.
А от затухания градиента может помочь пропускание градиента по частям, на сколько-то шагов по времени назад или вперёд, а не через всю нейросеть. Да, градиент будет не совсем точно считаться, и мы будем терять в качестве. Но это нам спасает память.

Обычная RNN имела множество проблем, в том числе в ней очень быстро затухала информация о предыдущих словах в предложении. Помимо этого были проблемы с затуханием/взрывом самого градиента.
Эти проблемы были частично решены в LSTM, предложенной в Long Short-Term Memory (Hochreiter & Schmidhuber, 1997) 🎓[article]
В обычной RNN в ячейке был только один путь передачи информации. На каждом шаге мы сливали информацию, накопленную с предыдущих шагов, с текущей:

При этом информация о предыдущих токенах очень быстро затухает, и теряется общая информация о предложении.
Структура ячейки LSTM намного сложнее. Здесь есть целых 4 линейных слоя, каждый из которых выполняет разные задачи.
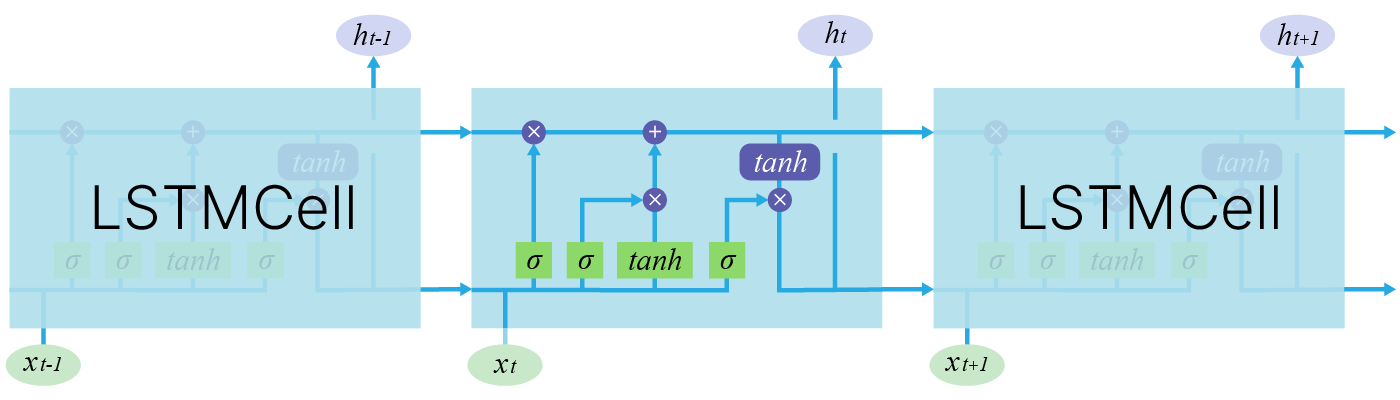

$\large f_t = σ(W_f \cdot [h_{t-1}, x_t] + b_f) - \text{forget gate}$
$\large i_t = σ(W_i \cdot [h_{t-1}, x_t] + b_i) - \text{input gate}$
$\large C^\prime_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_{C^\prime}) - \text{candidate cell state}$
$\large C_t = f_t\otimes C_{t-1} + i_t \otimes C^\prime_t - \text{cell state}$
$\large o_t = σ(W_o \cdot [h_{t-1}, x_t] + b_o) - \text{output gate}$
$\large h_t = o_t\otimes \tanh(C_t) - \text{ block output}$
Главное нововведение: в LSTM добавлен путь $c$, который по задумке должен этот общий контекст сохранять.
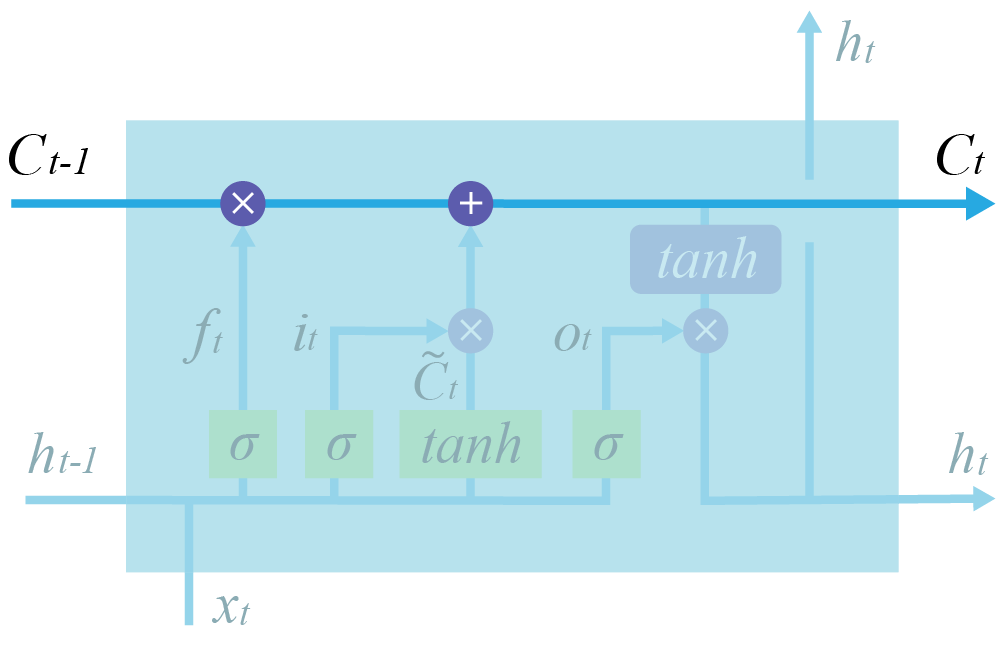
Другими словами, путь $c$ (cell state, иногда называется highway, магистраль) помогает нейросети сохранять важную информацию, встретившуюся в какой-то момент в предложении, все время, пока эта информация требуется.
По формулам также видно, как возросла сложность.
Интерфейс отличается от RNNCell количеством входов и выходов.
import torch
lstm_cell = torch.nn.LSTMCell(input_size=3, hidden_size=4)
input = torch.randn(1, 3) # batch, input_size
h_0 = torch.randn(1, 4)
c_0 = torch.randn(1, 4)
h, c = lstm_cell(input, (h_0, c_0)) # second arg is tuple
print("Shape of h:", h.shape) # batch, hidden_size
print("Shape of c:", c.shape) # batch, hidden_size
Shape of h: torch.Size([1, 4]) Shape of c: torch.Size([1, 4])
Отличие от RNN состоит в том, что кроме $h$ возвращается еще и $c$.
import torch.nn as nn
lstm = nn.LSTM(input_size=4, hidden_size=5)
input = torch.randn(3, 2, 4) # seq_len, batch, input_size
out, (h, c) = lstm(input) # h and c returned in tuple
print("Input shape:".ljust(15), input.shape)
print("Shape of h".ljust(15), h.shape) # batch, hidden_size
print("Shape of c".ljust(15), c.shape) # batch, hidden_size
print(
"Output shape:".ljust(15), out.shape
) # seq_len, batch, hidden_size : h for each element
Input shape: torch.Size([3, 2, 4]) Shape of h torch.Size([1, 2, 5]) Shape of c torch.Size([1, 2, 5]) Output shape: torch.Size([3, 2, 5])
Замечания
Посмотрим, как эта идея реализуется на практике. Далее в лекции подробно разберём работу отдельных блоков.
Зафиксируем seeds для воспроизводимости результатов:
import torch
import random
import numpy as np
def set_random_seed(seed):
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
np.random.seed(seed)
random.seed(seed)
set_random_seed(42)
Сгенерируем 30 различных синусоид с одинаковой частотой и амплитудой, но начинающиеся немного с разных точек на оси Х.
import numpy as np
N = 30 # number of samples
L = 300 # length of each sample (number of values for each sine wave)
T = 10 # width of the wave
x = np.empty((N, L), np.float32) # instantiate empty array
x[:] = np.arange(L) + np.random.randint(-4 * T, 4 * T, N).reshape(N, 1)
y = np.sin(x / 1.0 / T).astype(np.float32)
Сеть будет обучаться на 30 различных синусоидах.
import matplotlib.pyplot as plt
plt.plot(y[0], label="Sequense1")
plt.plot(y[1], label="Sequense2")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc="upper left")
plt.show()
Создадим класс модели и пройдёмся по его частям.
import torch
import torch.nn as nn
class LSTM(nn.Module):
def __init__(self, hidden_state=512):
super(LSTM, self).__init__()
self.hidden_state = hidden_state
# lstm1, lstm2, linear are all layers in the network
self.lstm1 = nn.LSTMCell(1, self.hidden_state)
self.lstm2 = nn.LSTMCell(self.hidden_state, self.hidden_state)
self.linear = nn.Linear(self.hidden_state, 1)
def forward(self, y, future_preds=0):
outputs, n_samples = [], y.size(0)
h_t = torch.zeros(n_samples, self.hidden_state, dtype=torch.float32)
c_t = torch.zeros(n_samples, self.hidden_state, dtype=torch.float32)
h_t2 = torch.zeros(n_samples, self.hidden_state, dtype=torch.float32)
c_t2 = torch.zeros(n_samples, self.hidden_state, dtype=torch.float32)
for time_step in y.split(1, dim=1):
# N, 1
h_t, c_t = self.lstm1(
time_step, (h_t, c_t)
) # initial hidden and cell states
h_t2, c_t2 = self.lstm2(h_t, (h_t2, c_t2)) # new hidden and cell states
output = self.linear(h_t2) # output from the last FC layer
outputs.append(output)
for i in range(future_preds):
# this only generates future predictions if we pass in future_preds>0
# mirrors the code above, using last output/prediction as input
h_t, c_t = self.lstm1(output, (h_t, c_t))
h_t2, c_t2 = self.lstm2(h_t, (h_t2, c_t2))
output = self.linear(h_t2)
outputs.append(output)
# transform list to tensor
outputs = torch.cat(outputs, dim=1)
return outputs
Инициализация:
time_step — количество признаков, описывающих входящий объект $x$,hidden_state — размер вектора контекста $h$.Мы определяем два слоя RNN, используя две ячейки RNNCell. В первую ячейку RNN мы подаём входные данные размером $1$.
В RNN нам не нужно передавать нарезанный массив входных данных. Нам не нужно скользящее окно для данных, поскольку вектора контекста обеспечивают сохранение состояния ячейки за нас.
h_0 — тензор, содержащий начальное скрытое состояние для каждого элемента в кортеже размера (batch, hidden_size).Размер батча определяется первым измерением входных данных, следовательно, берем n_samples = x.size(0).
Следующий шаг, пожалуй, самый трудный. Мы должны подать тензор соответствующей формы. Это будет тензор из m точек, где m — размер train в каждой последовательности.
a = torch.from_numpy(y[3:, :-1])
b = a.split(1, dim=1)
b[0].shape
torch.Size([27, 1])
Ещё один момент: мы обрабатываем $1$ элемент в строке, и, чтобы предсказать $300$-й элемент (и посчитать ошибку), мы должны остановиться на $299$-м. То же самое касается начала последовательности. По первому элементу предсказываем второй.
train_input = torch.from_numpy(y[3:, :-1]) # (27, 299)
train_target = torch.from_numpy(y[3:, 1:]) # (27, 299)
test_input = torch.from_numpy(y[:3, :-1]) # (3, 299)
test_target = torch.from_numpy(y[:3, 1:]) # (3, 299)
Цикл обучения приближен к стандартному.
Добавлена функция отрисовки предсказываемых синусоид для визуализации сходимости.
def draw(yi, n, i, future):
f, (ax1, ax2, ax3) = plt.subplots(1, 3, sharey=True, figsize=(12, 3))
plt.title(f"Step {i+1}")
plt.xlabel("x")
plt.ylabel("y")
ax1.plot(np.arange(n), yi[0][:n], "r", linewidth=2.0)
ax1.plot(np.arange(n, n + future), yi[0][n:], "r" + ":", linewidth=2.0)
ax2.plot(np.arange(n), yi[1][:n], "g", linewidth=2.0)
ax2.plot(np.arange(n, n + future), yi[1][n:], "g" + ":", linewidth=2.0)
ax3.plot(np.arange(n), yi[2][:n], "b", linewidth=2.0)
ax3.plot(np.arange(n, n + future), yi[2][n:], "b" + ":", linewidth=2.0)
plt.savefig("predict%d.png" % i, dpi=200)
plt.show()
plt.close()
def training_loop(
num_epochs,
model,
optimiser,
loss_fn,
train_input,
train_target,
test_input,
test_target,
):
for i in range(num_epochs):
def closure():
optimiser.zero_grad()
out = model(train_input)
loss = loss_fn(out, train_target)
loss.backward()
return loss
optimiser.step(closure)
with torch.no_grad():
future = 100
pred = model(test_input, future_preds=future)
# use all pred samples, but only go to 299
loss = loss_fn(pred[:, :-future], test_target)
y = pred.detach().numpy()
# draw figures
n = train_input.shape[1] # 299
draw(y, n, i, future)
# print the loss
out = model(train_input)
loss_print = loss_fn(out, train_target)
print("Step: {}, Loss: {}".format(i, loss_print))
import torch.optim as optim
model = LSTM(hidden_state=128)
criterion = nn.MSELoss()
optimiser = optim.LBFGS(model.parameters(), lr=0.01)
num_epochs = 20
training_loop(
num_epochs,
model,
optimiser,
criterion,
train_input,
train_target,
test_input,
test_target,
)
Step: 0, Loss: 0.16092360019683838
Step: 1, Loss: 0.0824916735291481
Step: 2, Loss: 0.05598531663417816
Step: 3, Loss: 0.037580814212560654
Step: 4, Loss: 0.020968766883015633
Step: 5, Loss: 0.008734678849577904
Step: 6, Loss: 0.005881512071937323
Step: 7, Loss: 0.004695284180343151
Step: 8, Loss: 0.004001234192401171
Step: 9, Loss: 0.003534492803737521
Step: 10, Loss: 0.0031468765810132027
Step: 11, Loss: 0.002781656803563237
Step: 12, Loss: 0.0023913588374853134
Step: 13, Loss: 0.0020202454179525375
Step: 14, Loss: 0.0017059240490198135
Step: 15, Loss: 0.0014443600084632635
Step: 16, Loss: 0.001212954637594521
Step: 17, Loss: 0.0010037912288680673
Step: 18, Loss: 0.0008010429446585476
Step: 19, Loss: 0.0005882977275177836
Хорошо бы ещё как-то улучшить обучение модели.

Последовательность можно пропустить через сеть два раза: в прямом и обратном направлении. Для этого создаётся слой, аналогичный входному, для обратного направления, и результат двух слоёв конкатенируется.

dummy_input = torch.randn((2, 1, 3)) # seq_len, batch, input_size
rnn = torch.nn.RNN(3, 2, bidirectional=True)
for t, p in rnn.named_parameters():
print(t, p.shape)
out, h = rnn(dummy_input)
# Concatenated Hidden states from both layers
print("Out:\n", out.shape)
# Hidden states last element from both : 2*num_layers*hidden_state
print("h:\n", h.shape)
weight_ih_l0 torch.Size([2, 3]) weight_hh_l0 torch.Size([2, 2]) bias_ih_l0 torch.Size([2]) bias_hh_l0 torch.Size([2]) weight_ih_l0_reverse torch.Size([2, 3]) weight_hh_l0_reverse torch.Size([2, 2]) bias_ih_l0_reverse torch.Size([2]) bias_hh_l0_reverse torch.Size([2]) Out: torch.Size([2, 1, 4]) h: torch.Size([2, 1, 2])
Как вы уже могли отметить, RNN ячейку можно инициализировать собственным начальным вектором. А затем подавать туда скрытое состояние на каждой итерации. Или не подавать.
Как так-то?
Да, цель скрытого состояния — закодировать историю. Допустим, ваши входные данные представляют собой последовательность данных со 2 по 11 день, и закодированная история в скрытом состоянии связана только с данными со 2 по 11 день. Таким образом, ваши батчи должны содержать всю историю, необходимую для каждого выходного прогноза.
При этом обязательно нужно сбросить скрытое состояние между батчами, если данные в них независимы. Вы не хотите, чтобы ваше скрытое состояние из вашего прошлого предсказания повлияло на следующее?
GRU (Gated Recurrent Unit)
Самая известная модификация LSTM — GRU. Она более компактна за счет сильных упрощений в сравнении со стандартной LSTM.
Главные изменения: объединены forget и input gates, слиты $h_t$ и $C_t$, которые в обычной LSTM только участвовали в формировании друг друга.
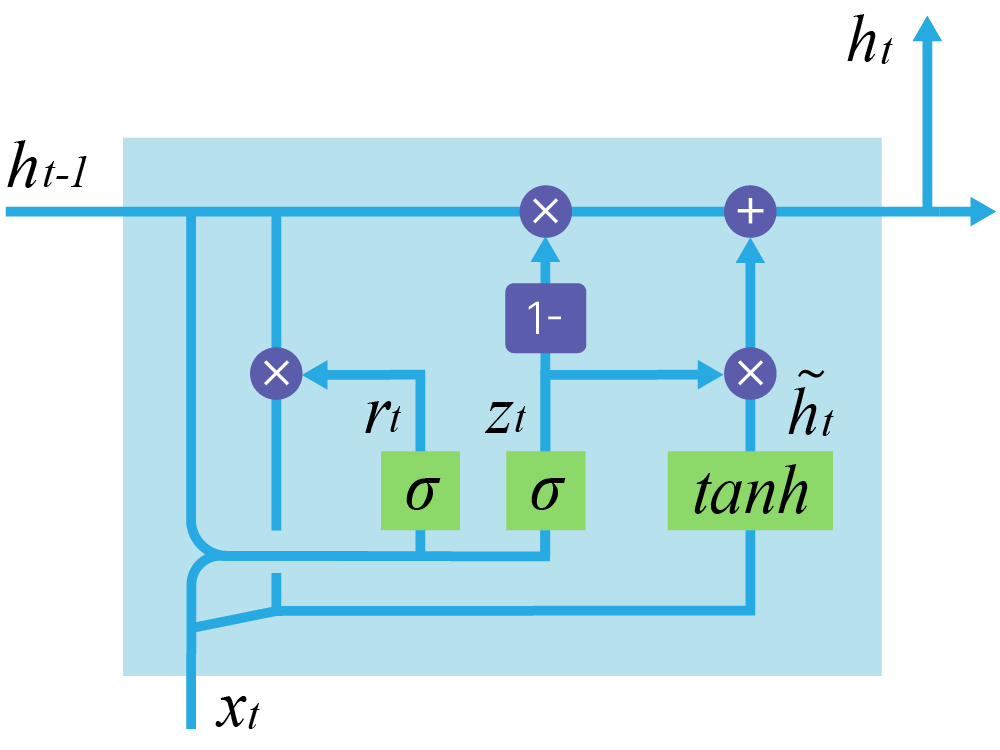
$\large z_t = \sigma(W_z \cdot [h_{t-1}, x_t])$
$\large r_t = \sigma(W_r \cdot [h_{t-1}, x_t])$
$\large \tilde h_t = \tanh(W \cdot [r_t * h_{t-1}, x_t])$
$\large h_t = (1-z_t) * h_{t-1} + z_t * \tilde h_t$
gru = torch.nn.GRU(input_size=4, hidden_size=3)
input = torch.randn(2, 1, 4) # seq_len, batch, input_size
h0 = torch.randn(1, 1, 3)
output, h = gru(input, h0)
print("Input shape:".ljust(15), input.shape)
print("Shape of h:".ljust(15), h.shape) # last h
print("Output shape:".ljust(15), output.shape) # seq_len = 2
Input shape: torch.Size([2, 1, 4]) Shape of h: torch.Size([1, 1, 3]) Output shape: torch.Size([2, 1, 3])
Практический опыт исследователей: иногда лучше работает GRU, иногда — LSTM. Точный рецепт успеха сказать нельзя.
Рекуррентная сеть может выдавать некий ответ на каждом шаге, однако мы можем:
Использовать только выданный на последнем (если нам нужно предсказать одно значение) — many-to-one.
Подавать в нейросеть токены (когда кончился исходный сигнал, подаем нулевые токены), пока она не сгенерирует токен, символизирующий остановку (many-to-many, one-to-many).
Делать различные комбинации, игнорируя часть выходов нейросети в начале её работы.
«One to one» — обычная нейронная сеть, не обязательно применять RNN в таком случае.
Более сложной является реализация «one to many», когда у нас есть всего один вход, и нам необходимо сформировать несколько выходов. Такой тип нейронной сети актуален, когда мы говорим о генерации музыки или текстов. Мы задаем начальное слово или начальный звук, а дальше модель начинает самостоятельно генерировать выходы, в качестве входа к очередной ячейке рассматривая выход с прошлой ячейки нейронной сети.
Если мы рассматриваем задачу классификации, то актуальна схема «many to one». Мы должны проанализировать все входы нейронной сети и только в конце определиться с классом.
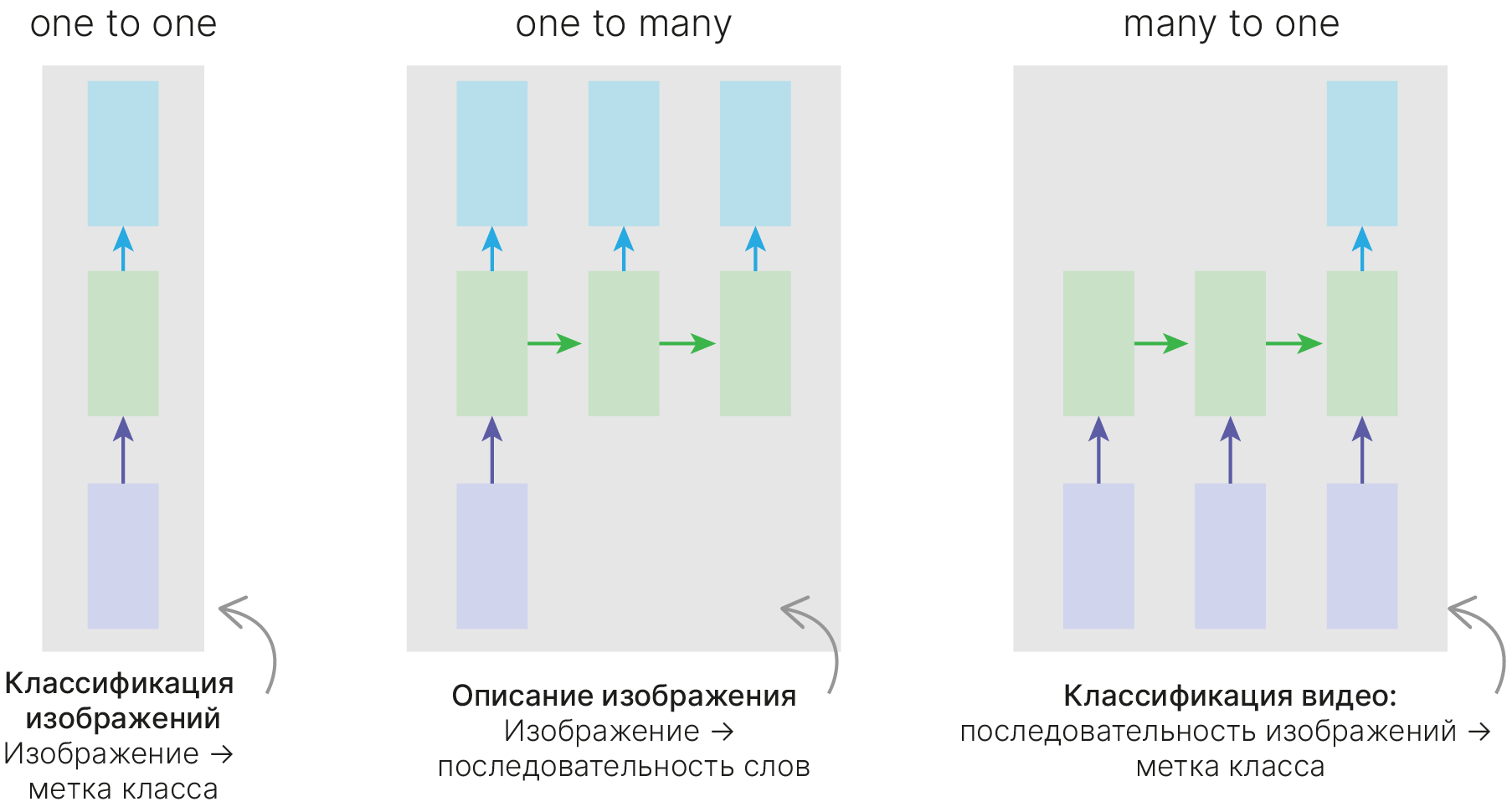
Схема «many to many», в которой количество выходов равно количеству входов нейронной сети. Обычно это задачи типа разметки исходной последовательности. Например, указать столицы городов, названия важных объектов, веществ и т.д., что относится к задачам вида NER (Named entity recogition).
Схема «many to many», в которой количество выходов нейронной сети не равно количеству входов. Это актуально в машинном переводе, когда одна и та же фраза может иметь разное количество слов в разных языках (т.е. это реализует схему кодировщик-декодировщик). Кодировщик получает данные различной длины — например, предложение на английском языке. С помощью скрытых состояний он формирует из исходных данных вектор, который затем передаётся в декодировщик. Последний, в свою очередь, генерирует из полученного вектора выходные данные — исходную фразу, переведённую на другой язык.
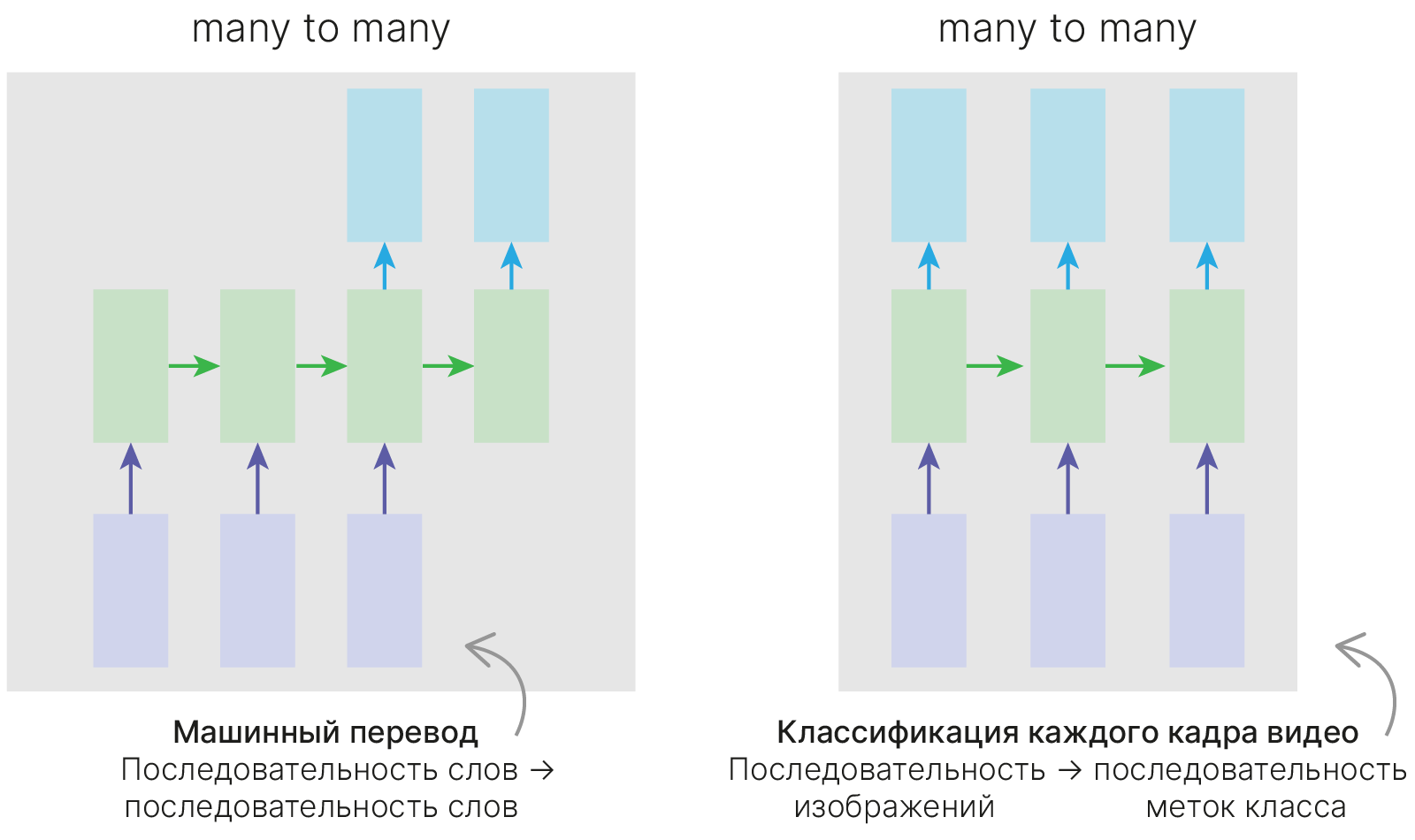
Можно объединять разные подходы. Сначала генерируем некий $h$, который содержит сжатую информацию о том, что было подано в нейросеть, а затем подаем его в нейросеть «one to many», которая генерирует, к примеру, перевод того текста, что был подан первой части нейросети.
Среди NLP-задач можно выделить такие группы:

В зависимости от источника ввода полученный текст может иметь свои особенности. Автоматическое распознавание приводит к ошибкам распознавания и разметки страниц; текст из социальных сетей — большое количество сокращений, смайлов, хэштегов, упоминаний и пр.
Начнем с относительно простой задачи — посимвольной генерации текста. Как правило, конвейер обработки текста содержит в себе следующие 5 блоков. К ним, в зависимости от задачи, добавляются дополнительные пункты.
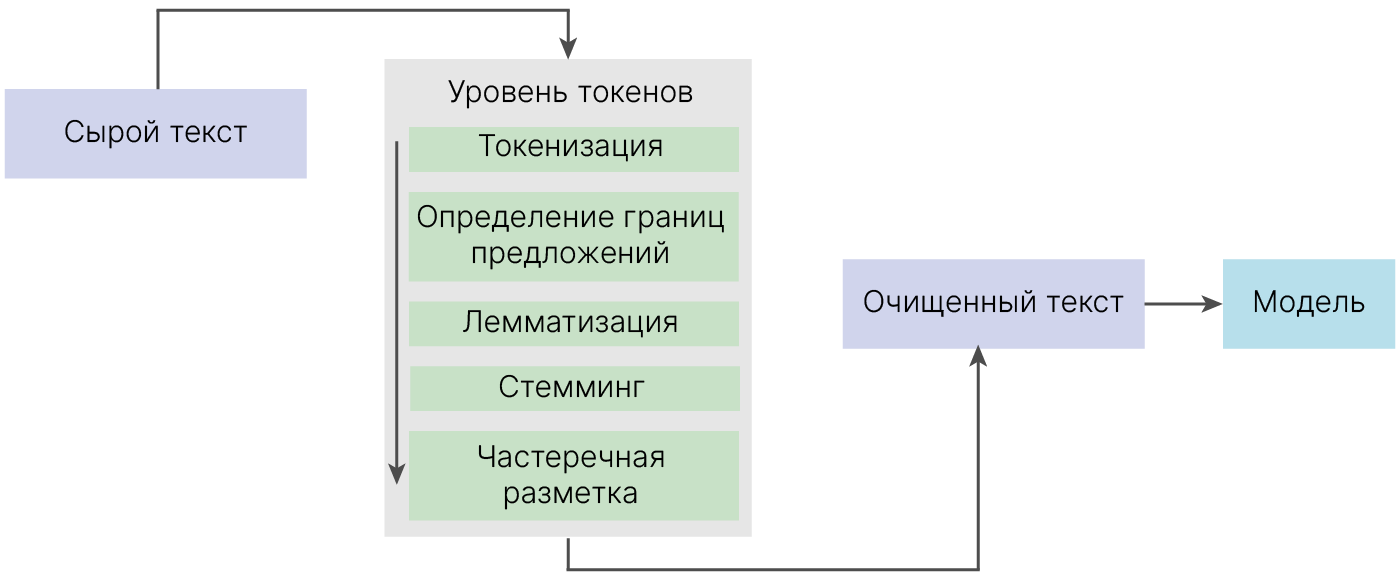
Постановка задачи: предсказать следующий символ в последовательности.
исходный текст: 'hey how are you'
искаженный текст: 'hey how are yo'
Верное предсказание: 'u'
Очень похоже на то, что мы делали ранее с временными рядами. Инференс модели будет выглядеть так:
В нашей учебной задаче мы сократим до минимума выполняемые операции по подготовке данных для модели.
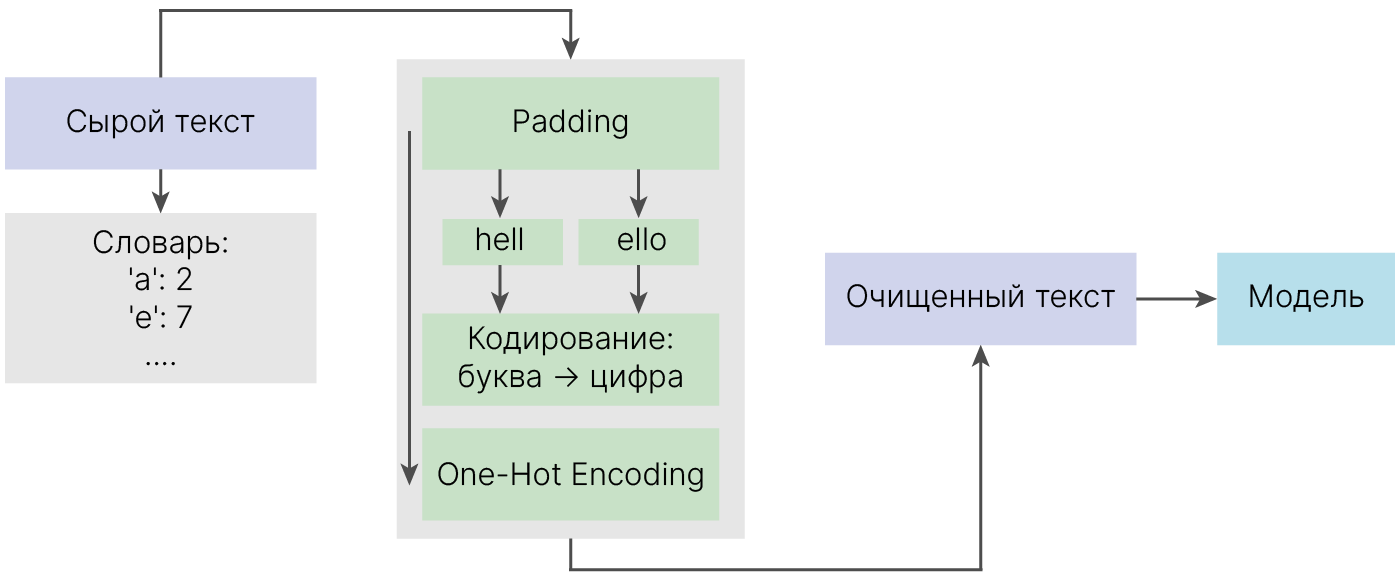
import pprint
text = ["hey how are you", "good i am fine", "have a nice day"]
# Join all the sentences together and extract the unique characters
# from the combined sentences
chars = set("".join(text))
# Creating a dictionary that maps integers to the characters
int2char = dict(enumerate(chars))
# Creating another dictionary that maps characters to integers
char2int = {char: ind for ind, char in int2char.items()}
print("Dictionary for mapping character to the integer:")
pprint.pprint(char2int)
Dictionary for mapping character to the integer:
{' ': 2,
'a': 15,
'c': 6,
'd': 16,
'e': 13,
'f': 12,
'g': 10,
'h': 4,
'i': 14,
'm': 9,
'n': 3,
'o': 0,
'r': 8,
'u': 11,
'v': 5,
'w': 1,
'y': 7}
Вместо ASCII символа, каждой букве мы сопоставили номер.
RNN допускают работу с данными переменной длины. Но чтобы поместить предложения в batch, надо их выровнять.
Обычно размер батча делают равным самому длинному предложению, а остальные просто дополняют пробелами (или спецсимволами) до этого размера. Также хорошей идеей будет отметить специальным символом начало предложения.
lengths = [len(sent) for sent in text]
maxlen = max(lengths)
print(f"The longest string has {maxlen} characters.\n")
print(f"Initial texts:\n{text}")
# A simple loop that loops through the list of sentences and adds
# a ' ' whitespace until the length of the sentence matches
# the length of the longest sentence
for i in range(len(text)):
while len(text[i]) < maxlen:
text[i] += " "
print(f"Resulting texts:\n{text}")
The longest string has 15 characters. Initial texts: ['hey how are you', 'good i am fine', 'have a nice day'] Resulting texts: ['hey how are you', 'good i am fine ', 'have a nice day']
В качестве входа будем использовать предложение без последнего символа:
'hey how are yo'
В качестве результата — предложение, в котором он сгенерирован:
'ey how are you'
# Creating lists that will hold our input and target sequences
input_seq = []
target_seq = []
for i in range(len(text)):
# Remove last character for input sequence
input_seq.append(text[i][:-1])
# Remove first character for target sequence
target_seq.append(text[i][1:])
print("Input sequence:".ljust(18), f"'{input_seq[i]}'")
print("Target sequence:".ljust(18), f"'{target_seq[i]}'")
print()
Input sequence: 'hey how are yo' Target sequence: 'ey how are you' Input sequence: 'good i am fine' Target sequence: 'ood i am fine ' Input sequence: 'have a nice da' Target sequence: 'ave a nice day'
Теперь символы надо перевести в числа. Для этого мы уже построили словарь.
P.S. Запускать блок только один раз.
for i in range(len(text)):
input_seq[i] = [char2int[character] for character in input_seq[i]]
target_seq[i] = [char2int[character] for character in target_seq[i]]
print("Encoded input sequence:".ljust(25), input_seq[i])
print("Encoded target sequence:".ljust(25), target_seq[i])
print()
Encoded input sequence: [4, 13, 7, 2, 4, 0, 1, 2, 15, 8, 13, 2, 7, 0] Encoded target sequence: [13, 7, 2, 4, 0, 1, 2, 15, 8, 13, 2, 7, 0, 11] Encoded input sequence: [10, 0, 0, 16, 2, 14, 2, 15, 9, 2, 12, 14, 3, 13] Encoded target sequence: [0, 0, 16, 2, 14, 2, 15, 9, 2, 12, 14, 3, 13, 2] Encoded input sequence: [4, 15, 5, 13, 2, 15, 2, 3, 14, 6, 13, 2, 16, 15] Encoded target sequence: [15, 5, 13, 2, 15, 2, 3, 14, 6, 13, 2, 16, 15, 7]
Теперь из чисел надо сделать вектора.
Причина — подача чисел даст модели ложное знание об отношениях между объектами по типу "буква а в два раза больше буквы б". Нам же нужно равномерно распределить наши представления в некотором пространстве.
import numpy as np
dict_size = len(char2int)
seq_len = maxlen - 1
batch_size = len(text)
def one_hot_encode(sequence, dict_size, seq_len, batch_size):
# Creating a multi-dimensional array of zeros with the desired output shape
features = np.zeros((batch_size, seq_len, dict_size), dtype=np.float32)
# Replacing the 0 at the relevant character index with a 1 to represent that character
for i in range(batch_size):
for u in range(seq_len):
features[i, u, sequence[i][u]] = 1
return features
input_seq = one_hot_encode(input_seq, dict_size, seq_len, batch_size)
print(
"Input shape: {} --> (Batch Size, Sequence Length, One-Hot Encoding Size)".format(
input_seq.shape
)
)
print(input_seq[0])
Input shape: (3, 14, 17) --> (Batch Size, Sequence Length, One-Hot Encoding Size) [[0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
Каждый символ закодировали вектором. Не слишком экономно, зато удобно умножать на матрицу весов.
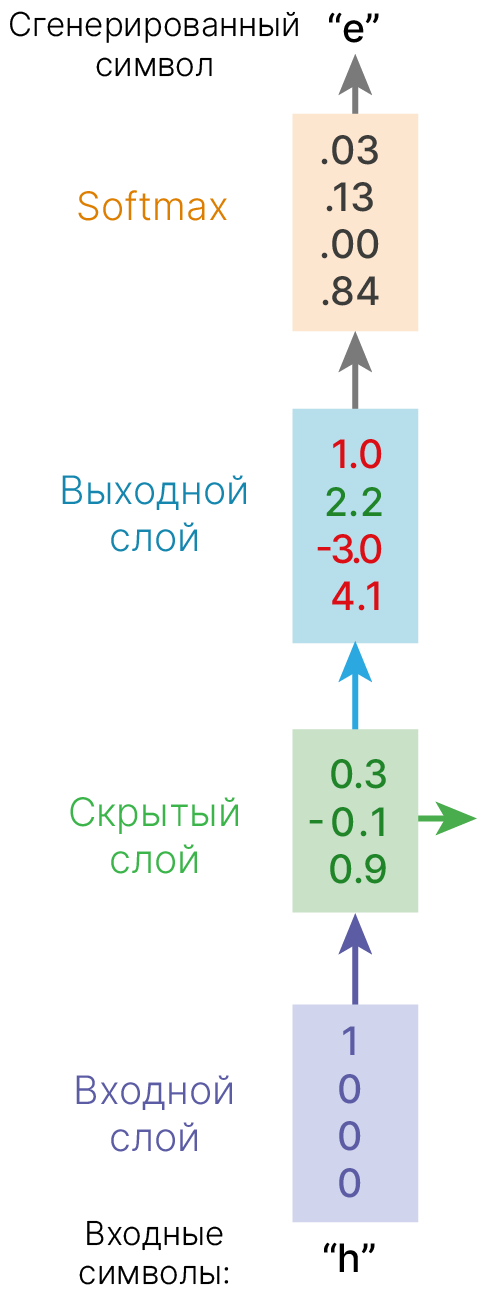
Пример: Language Modeling
Кодируем буквы при помощи one-hot кодирования и подаем на входной слой.
$\begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} \\ w_{21} & w_{22} & w_{23} & w_{24} \\ w_{31} & w_{32} & w_{33} & w_{34} \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0\\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} w_{11} \\ w_{21} \\ w_{31}\end{bmatrix}$
Таким образом, обработка

Умножение матрицы на one-hot представление просто достает соответствующую ненулевому значению колонку из матрицы весов. Поэтому часто вместо написания двух отдельных слоев (one-hot + линейного) делают просто слой, называемый Embedding Layer.
# Convert data to tensor
import torch
input_seq = torch.Tensor(input_seq)
target_seq = torch.Tensor(target_seq)
import torch.nn as nn
class NextCharacterGenerator(nn.Module):
def __init__(self, input_size, output_size, hidden_dim, n_layers):
super().__init__()
# RNN Layer
self.rnn = nn.RNN(input_size, hidden_size=hidden_dim, batch_first=True)
# Fully connected layer
self.fc = nn.Linear(hidden_dim, output_size)
def forward(self, x):
batch_size = x.size(0)
# Initializing hidden state for first input using method defined below
hidden_0 = torch.zeros(
1, batch_size, self.rnn.hidden_size
) # 1 correspond to number of layers
# Passing in the input and hidden state into the model and obtaining outputs
out, hidden = self.rnn(x, hidden_0)
# Reshaping the outputs such that it can be fit into the fully connected layer
# Need Only if n_layers > 1
out = out.contiguous().view(-1, self.rnn.hidden_size)
out = self.fc(out)
return out, hidden
# Instantiate the model with hyperparameters
model = NextCharacterGenerator(
input_size=dict_size, output_size=dict_size, hidden_dim=12, n_layers=1
)
# Define hyperparameters
num_epochs = 100
# Define Loss, Optimizer
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
# Training Run
for epoch in range(1, num_epochs + 1):
optimizer.zero_grad() # Clears existing gradients from previous epoch
output, hidden = model(input_seq)
loss = criterion(output, target_seq.view(-1).long())
loss.backward() # Does backpropagation and calculates gradients
optimizer.step() # Updates the weights accordingly
if epoch % 10 == 0:
print(f"Epoch: {epoch}/{num_epochs}".ljust(20), end=" ")
print("Loss: {:.4f}".format(loss.item()))
Epoch: 10/100 Loss: 2.4534 Epoch: 20/100 Loss: 2.1249 Epoch: 30/100 Loss: 1.7164 Epoch: 40/100 Loss: 1.3150 Epoch: 50/100 Loss: 0.9692 Epoch: 60/100 Loss: 0.6836 Epoch: 70/100 Loss: 0.4718 Epoch: 80/100 Loss: 0.3277 Epoch: 90/100 Loss: 0.2334 Epoch: 100/100 Loss: 0.1742
def predict(model, character):
# One-hot encoding our input to fit into the model
character = np.array([[char2int[c] for c in character]])
character = one_hot_encode(character, dict_size, character.shape[1], 1)
character = torch.from_numpy(character)
out, hidden = model(character)
# print(out.shape)
# print(out)
prob = nn.functional.softmax(out[-1], dim=0).data
# Taking the class with the highest probability score from the output
char_ind = torch.max(prob, dim=0)[1].item()
return int2char[char_ind], hidden
def sample(model, out_len, start="hey"):
model.eval() # eval mode
start = start.lower()
# First off, run through the starting characters
chars = [ch for ch in start]
size = out_len - len(chars)
# Now pass in the previous characters and get a new one
for _ in range(size):
char, h = predict(model, chars)
chars.append(char)
return "".join(chars)
sample(model, 15, "good")
'good i am fine '
Попробуем сгенерировать несколько вариантов предложения.
for _ in range(3):
print(sample(model, 15, "good"))
good i am fine good i am fine good i am fine
Так получается, потому что сеть инициализирована нулями и никакой случайности нет. Даже если мы добавим в датасет ещё предложение, начинающиеся с good, результат не изменится. Также сеть переобучилась на небольшом датасете.
Один из ключевых этапов в обработке текста — токенизация. На этом этапе происходит разделение текста на отдельные единицы — предложения и слова. Затем создается словарь, в который заносятся уникальные лексемы, встретившиеся в корпусе или тексте. На этих этапах можно столкнуться с несколькими проблемами.
Проблема 1. Размер словаря
Самый простой способ токенизации — назначить каждому уникальному слову своё число. Но есть проблема: слов и их форм миллионы, и поэтому словарь таких слов получится чересчур большим, а это будет затруднять обучение модели.
Можно разбивать текст не на слова, а на отдельные буквы (char-level tokenization), тогда в словаре будет всего несколько десятков токенов, НО в таком случае уже сам текст после токенизации будет слишком длинным, а это тоже затрудняет обучение.
Проблема 2. Богатая морфология
"Нейросеть", "сетка", "сеть" являются разными словами, но имеют схожий смысл. Эту проблему классически всегда решал этап стемминга (удаление суффикса, приставки, окончания) или лемматизации (приведение слова к канонической форме).
Проблема 3. Сложные слова
Но все проблемы эти этапы не решают. В германских языках (в английском, немецком, шведском и т.д.) очень продуктивно образовываются новые сложные слова. Значения таких слов выводятся из значения их элементов. Их можно создавать бесконечно долго, и большинство из них не зафиксировано в «бумажном» словаре.

При работе с этими языками сложность также возникает на этапе составления словаря. При составлении словаря модели ориентируются на частотность (например, сохраняем слово, если оно встретилось чаще пяти раз), поэтому не будут запоминать такое длинное и сложное слово.
Проблема 4: Границы слова
Для нас, привыкших к языкам европейского типа, слово — это набор букв между пробелами и знаками препинания. Но в английском языке многие сложные слова пишутся раздельно, а в японском, наоборот, между словами вообще нет пробелов. Поэтому универсальный токенизатор создать было нелегко.
TF-IDF — способ численного представления документа, оценивает важность слова в контексте документа. Состоит из двух множителей $\text{TF}$ и $\text{IDF}$.
Первая идея TF-IDF — если слово часто встречается в документе, оно важное. За это отвечает $TF$.
$\text{TF}$ (term frequency) — частота вхождения слова в документ, для которого рассчитывается значение:
$$\large \text{TF}(t, d) = \frac{n_t}{\sum_{k}n_k},$$$n_t$ — количество повторов слова $t$ в документе $d$,
$\sum_{k}n_k$ — общее количество слов $t$ в документе $d$ с повторами.
Вторая идея TF-IDF — если слово встречается во многих документах, его ценность снижается.
Пример: местоимения встречаются в большинстве текстов, но не несут смысловой нагрузки.
За это отвечает $\text{IDF}$.
$\text{IDF}$ (inverse document frequency) — логарифм обратной частоты вхождения слова в документы. $$\large \text{IDF}(t, D) = \log{\frac{|D|}{|\{d_i \in D| t_i \in d_i \}|}},$$
где $|D|$ — число документов в коллекции, $|\{d_i \in D| t_i \in d_i \}|$ — число документов в коллекции со словом $t$.
Итоговая формула: $$\large \text{TF-IDF}(t, d, D) = \text{TF}(t,d)⋅\text{IDF}(t, D)$$
Пример работы TfidfVectorizer из sklearn 🛠️[doc].
Каждому документу сопоставляется вектор, равный длине словаря. Ненулевые значения вектора хранятся в виде разреженных матриц scipy.sparse.csr_matrix 🛠️[doc].
from sklearn.feature_extraction.text import TfidfVectorizer
corpus = [
"This is the first document.",
"This document is the second document.",
"And this is the third one.",
"Is this the first document?",
]
vectorizer = TfidfVectorizer()
x = vectorizer.fit_transform(corpus)
print("Tf-idf dictionary:", vectorizer.get_feature_names_out())
print("Tf-idf dictionary len:", len(vectorizer.get_feature_names_out()))
print("Tf-idf shape:", x.shape)
print("Tf-idf type:", type(x))
print("Tf-idf values:", x)
Tf-idf dictionary: ['and' 'document' 'first' 'is' 'one' 'second' 'the' 'third' 'this'] Tf-idf dictionary len: 9 Tf-idf shape: (4, 9) Tf-idf type: <class 'scipy.sparse._csr.csr_matrix'> Tf-idf values: (0, 1) 0.46979138557992045 (0, 2) 0.5802858236844359 (0, 6) 0.38408524091481483 (0, 3) 0.38408524091481483 (0, 8) 0.38408524091481483 (1, 5) 0.5386476208856763 (1, 1) 0.6876235979836938 (1, 6) 0.281088674033753 (1, 3) 0.281088674033753 (1, 8) 0.281088674033753 (2, 4) 0.511848512707169 (2, 7) 0.511848512707169 (2, 0) 0.511848512707169 (2, 6) 0.267103787642168 (2, 3) 0.267103787642168 (2, 8) 0.267103787642168 (3, 1) 0.46979138557992045 (3, 2) 0.5802858236844359 (3, 6) 0.38408524091481483 (3, 3) 0.38408524091481483 (3, 8) 0.38408524091481483
На практике
Тексты токенизируются и нормализуются. Если мы решаем работать с N-граммами, то вместо токенизации или после неё выделяем N-граммы.
Проходимся по всей коллекции документов и для каждого слова подсчитываем, в каком количестве документов оно встретилось. Если у нас большая коллекция, то словарь может получиться просто гигантским, особенно если мы работаем с N-граммами, поэтому периодически, во время построения или после этой процедуры, мы должны выбросить из словаря всё, что считаем неинформативным — слишком редкие и слишком частые слова.
Затем начинаем строить матрицу признаков. Каждая строчка этой матрицы соответствует документу, а каждый столбец — статистике встречаемости этого слова в документе. Таким образом, для каждого документа мы считаем частоты слов в нём и записываем в соответствующие ячейки таблицы веса слов по указанной формуле.
Переходим к следующему документу.
Таким образом, TF-IDF — это способ взвешивания и отбора категориальных признаков в задачах машинного обучения — не только в классификации и не только для текстов. Надо заметить, что TF-IDF никак не использует информацию о метке объекта — это одновременно и преимущество, и недостаток. Преимущество заключается в том, что мы можем использовать TF-IDF, не имея меток, то есть задачах обучения без учителя. Недостаток — в том, что мы теряем информацию или недостаточно эффективно её используем.
Когда TF-IDF может быть неэффективен:
Отсутствие семантической информации: TF-IDF не учитывает семантические связи между словами, что может привести к ограниченной способности понимания смысла текста.
Чувствительность к длине документа: длинные документы могут иметь более высокие значения TF, даже если ключевые слова встречаются реже. В таких случаях TF-IDF может недооценить важность конкретных слов.

Word2Vec — нейронная сеть из двух слоев, которая обрабатывает текст, преобразуя его в числовые “векторизованные” слова. Входные данные w2v — это громадный текстовый корпус, из которого на выходе мы получаем пространство векторов (линейное пространство), размерность которого обычно достигает сотен, где каждое уникальное слово в корпусе представлено вектором из сгенерированного пространства.
Мы учим сеть так, что вектора, соответствующие похожим словам, располагаются близко в новом пространстве, и над ними работают векторные операции.

Такие операции не приводят к точному соответствию, однако получаемые вектора оказываются самыми похожими.
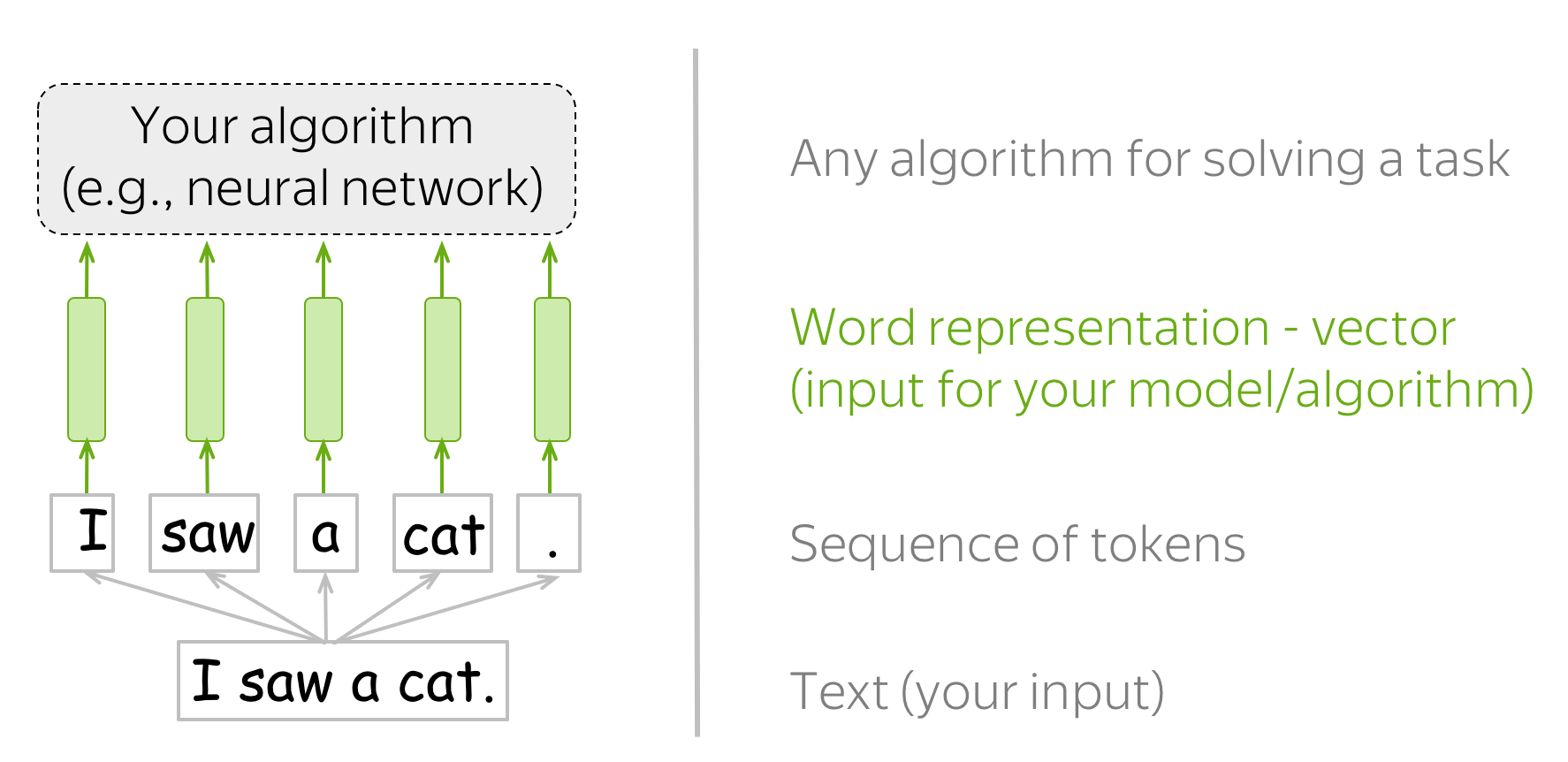
Ранее мы применяли OneHotEncoding для представления наших слов. Проблемы возникают, когда пространство объектов начинает расти и у нас возникают огромные разреженные матрицы.
Кроме того, некоторые объекты у нас сразу могут быть ближе: семантически "король" и "королева" отличаются только полом, различие между словами "король" и "стул" заметно выше.
Поэтому мы можем переводить наши слова в вектора меньшей размерности, которые при этом будут сравнимы между собой с помощью модуля nn.Embedding 🛠️[doc].
# Let's say you have 2 sentences (lowercased, punctuations removed):
sentences = "i am new to pytorch i am having fun"
words = sentences.split(" ")
print(f"All words: {words} \n")
vocab = set(words) # create a vocabulary
vocab_size = len(vocab)
print(f"Vocabulary (unique words): {vocab} \n")
print(f"Vocabulary size: {vocab_size} \n")
# map words to unique indices
word2idx = {word: ind for ind, word in enumerate(vocab)}
print(f"Word-to-id dictionary: {word2idx} \n")
encoded_sentences = [word2idx[word] for word in words]
print(f"Encoded sentences: {encoded_sentences}")
# let's say you want embedding dimension to be 3
emb_dim = 3
All words: ['i', 'am', 'new', 'to', 'pytorch', 'i', 'am', 'having', 'fun']
Vocabulary (unique words): {'new', 'am', 'pytorch', 'having', 'fun', 'i', 'to'}
Vocabulary size: 7
Word-to-id dictionary: {'new': 0, 'am': 1, 'pytorch': 2, 'having': 3, 'fun': 4, 'i': 5, 'to': 6}
Encoded sentences: [5, 1, 0, 6, 2, 5, 1, 3, 4]
Теперь нейросетевой слой эмбеддингов может быть определён так:
import torch
import torch.nn as nn
emb_layer = nn.Embedding(vocab_size, emb_dim)
word_vectors = emb_layer(torch.LongTensor(encoded_sentences))
print(f"Shape of encoded sentences: {word_vectors.shape} \n")
print(f"Shape of weigths: {emb_layer.weight.shape}")
Shape of encoded sentences: torch.Size([9, 3]) Shape of weigths: torch.Size([7, 3])
Этот код инициализирует эмбеддинги согласно нормальному распределению (со средним значением 0 и дисперсией 1). Таким образом, пока что никакого различия или сходства между векторами нет.
word_vectors — тензор размером (9, 3). 9 слов в датасете, размер 3 задан нами.
emb_layer имеет 1 обучаемый параметр weight, который по умолчанию True. Можем проверить так:
emb_layer.weight.requires_grad
True
Если мы не хотим обучать этой слой (например, используем заранее обученные эмбеддинги), мы можем заморозить его веса:
emb_layer.weight.requires_grad = False
Если мы хотим использовать заранее определённые веса:
# predefined weights
weight = torch.FloatTensor([[0.1, 0.2, 0.3], [0.4, 0.5, 0.6]])
print(weight.shape)
embedding = nn.Embedding.from_pretrained(weight)
# get embeddings for ind 0 and 1
embedding(torch.LongTensor([0, 1]))
torch.Size([2, 3])
tensor([[0.1000, 0.2000, 0.3000],
[0.4000, 0.5000, 0.6000]])
Скачаем уже готовые веса модели Word2Vec, обученные на датасете Google News, состоящeм из 100 миллиардов слов:
# Source: https://drive.google.com/file/d/0B7XkCwpI5KDYNlNUTTlSS21pQmM/edit?resourcekey=0-wjGZdNAUop6WykTtMip30g
!wget -q https://edunet.kea.su/repo/EduNet-web_dependencies/weights/GoogleNews-vectors-negative300.bin.gz
!gunzip -q GoogleNews-vectors-negative300.bin.gz
from gensim.models import KeyedVectors
wordvector_path = "GoogleNews-vectors-negative300.bin"
word_vectors = KeyedVectors.load_word2vec_format(wordvector_path, binary=True)
weights = torch.FloatTensor(word_vectors.vectors)
weights.shape
torch.Size([3000000, 300])
embedding = nn.Embedding.from_pretrained(weight)
input = torch.LongTensor([0, 1])
embedding(input)
tensor([[0.1000, 0.2000, 0.3000],
[0.4000, 0.5000, 0.6000]])
Также мы можем воспользоваться библиотекой TorchText 🛠️[doc]. Возьмём таблицу весов поменьше, всего 10000 наиболее встречающихся слов. Зададим длину тензора — 50.
import torchtext
glove = torchtext.vocab.GloVe(
name="6B", dim=50, max_vectors=10000
) # use 10k most common words
.vector_cache/glove.6B.zip: 862MB [02:44, 5.25MB/s] 100%|█████████▉| 9999/10000 [00:00<00:00, 31607.97it/s]
Если обратиться к документации, мы увидим, что 6В — это лишь один из вариантов весов 🛠️[doc].
glove_emb = nn.Embedding.from_pretrained(glove.vectors)
input = torch.LongTensor([0, 1])
glove_emb(input).shape
torch.Size([2, 50])
Код нейросети со слоем nn.Embedding выглядит следующим образом:
class RNN_with_Embedding_Layer(nn.Module):
def __init__(self, input_size, hidden_size, num_classes):
super(RNN_with_Embedding_Layer, self).__init__()
self.emb = nn.Embedding.from_pretrained(glove.vectors)
self.hidden_size = hidden_size
self.rnn = nn.RNN(input_size, hidden_size, batch_first=True)
self.fc = nn.Linear(hidden_size, num_classes)
def forward(self, x):
# Look up the embedding
x = self.emb(x)
# Set an initial hidden state
h0 = torch.zeros(1, x.size(0), self.hidden_size)
# Forward propagate the RNN
out, _ = self.rnn(x, h0)
# Pass the output of the last time step to the classifier
out = self.fc(out[:, -1, :])
return out
model = RNN_with_Embedding_Layer(input_size=50, hidden_size=128, num_classes=3)
print(model)
RNN_with_Embedding_Layer( (emb): Embedding(10000, 50) (rnn): RNN(50, 128, batch_first=True) (fc): Linear(in_features=128, out_features=3, bias=True) )
Размер словаря — гиперпараметр. Как его выбрать?
Закон Ципфа — эмпирическая закономерность распределения частоты слов естественного языка: если все слова языка в достаточно большом осмысленном тексте упорядочить по убыванию частоты их использования, то частота слова в таком списке окажется приблизительно обратно пропорциональной его порядковому номеру. Плотность распределения Ципфа:
$$\large f(\text{rank}, s, N) = \frac {1}{Z(s,N)\text{rank}^s},$$где $\text{rank}$ — порядковый номер слова после сортировки по убыванию частоты, $s$ — коэффициент скорости убывания вероятности, $N$ — количество слов, $Z(s,N)= \sum ^N _{i=1} i^{-s}$ — нормализационная константа.
Из этого всего можно сделать два практических вывода:
Частотные — слабо информативны, так как встречаются практически во всех документах.
Редкие — слова очень редки, и поэтому они ненадёжны в качестве факторов при принятии решений.
Следовательно, нужно придерживаться баланса частотности и информативности. Основная идея в том, что чем чаще слово встречается в документе, тем более оно характерно для этого документа, тем лучше описывает его тематику. С другой стороны, чем это слово реже встречается в корпусе, в выборке документов, тем оно более специфично и информативно. За этот баланс отвечают две величины: TF и IDF.
Изначально алгоритм компрессии BPE позволяет моделям узнавать как можно больше слов при ограниченном объеме словаря.
Повторять, пока не достигли ограничения на размер словаря:
Назначаем новым токеном объединение двух существующих токенов, которое встречается чаще других пар в корпусе (встречаются вместе).
В применении BPE возможны разные варианты. Один из естественных – идём по всем токенам по убыванию частоты, находим соответствующую последовательность символов в корпусе, заменяем на токен.
Этот же способ помогает решить проблему OOV (out of vocabulary). В обучающей выборке может не быть слова Unfriendly, но поскольку Unfriendly = Un + friend + ly, мы можем рассчитывать, что сеть будет правильно обрабатывать / генерировать и слово целиком.
Модели глубокого обучения обычно требуют большого количества данных для обучения.
Вместо того, чтобы тратить дни на сбор данных вручную, мы можем использовать методы аугментации для автоматической генерации новых примеров из уже имеющихся.
Важный момент: при обучении модели мы используем разбиение данных на train-val-test. Аугментации стоит применять только на train. Почему так? Конечная цель обучения нейросети — это применение на реальных данных, которые сеть не видела. Поэтому для адекватной оценки качества модели валидационные и тестовые данные изменять не нужно.
В любом случае, test должен быть отделен от данных еще до того, как они попали в DataLoader или нейросеть.
Другое дело, что аугментации на тесте можно использовать как метод ансамблирования в случае классификации. Можно взять sample → создать несколько его копий → по-разному их аугментировать → предсказать класс на каждой из этих аугментированных копий → а потом выбрать наиболее вероятный класс голосованием (такой функционал реализован, например, в YOLOv5 🐾[git], о которой речь пойдет в следующих лекциях).
Рассмотрим несколько примеров аугментаций аудио. С полным списком можно ознакомиться здесь: audiomentations 🐾[git].
Установим библиотеку и посмотрим на пример
!pip install -q audiomentations
!wget -q https://edunet.kea.su/repo/EduNet-web_dependencies/dev-2.0/L09/audio_example.wav
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 82.3/82.3 kB 2.7 MB/s eta 0:00:00
from IPython.display import Audio
# Get input audio
input_audio = "/content/audio_example.wav"
display(Audio(input_audio))
import librosa
data, sr = librosa.load("/content/audio_example.wav") # sr - sampling rate
from audiomentations import AddGaussianSNR
augment = AddGaussianSNR(min_snr_in_db=3, max_snr_in_db=7, p=1)
# Augment/transform the audio data
augmented_data = augment(samples=data, sample_rate=sr)
display(Audio(augmented_data, rate=sr))
Сравним волновые картины и спектрограммы
import numpy as np
from scipy.signal import spectrogram
from matplotlib import pyplot as plt
def produce_plots(input_audio_arr, aug_audio, sr):
f, t, Sxx_in = spectrogram(
input_audio_arr, fs=sr
) # Compute spectrogram for the original signal (f - frequency, t - time)
f, t, Sxx_aug = spectrogram(aug_audio, fs=sr)
fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(20, 5))
ax[0, 0].plot(input_audio_arr)
ax[0, 0].set_xlim(0, len(input_audio_arr))
ax[0, 0].set_xticks([])
ax[0, 0].set_title("Original audio")
ax[0, 1].plot(aug_audio)
ax[0, 1].set_xlim(0, len(input_audio_arr))
ax[0, 1].set_xticks([])
ax[0, 1].set_title("Augmented audio")
ax[1, 0].imshow(
np.log(Sxx_in),
extent=[t.min(), t.max(), f.min(), f.max()],
aspect="auto",
cmap="inferno",
)
ax[1, 0].set_ylabel("Frequecny, Hz")
ax[1, 0].set_xlabel("Time,s")
ax[1, 1].imshow(
np.log(Sxx_aug, where=Sxx_aug > 0),
extent=[t.min(), t.max(), f.min(), f.max()],
aspect="auto",
cmap="inferno",
)
ax[1, 1].set_ylabel("Frequecny, Hz")
ax[1, 1].set_xlabel("Time,s")
plt.subplots_adjust(hspace=0)
plt.show()
produce_plots(data, augmented_data, sr)
from audiomentations import TimeStretch
augment = TimeStretch(min_rate=0.8, max_rate=1.5, p=1)
augmented_data = augment(data, sample_rate=sr)
display(Audio(augmented_data, rate=sr))
produce_plots(data, augmented_data, sr)
Изменение тональности:
from audiomentations import PitchShift
augment = PitchShift(min_semitones=1, max_semitones=12, p=1)
augmented_data = augment(data, sample_rate=sr)
display(Audio(augmented_data, rate=sr))
Как и в случае с картинками, мы можем совмещать несколько аугментаций вместе
from audiomentations import Compose, AddGaussianNoise
augment = Compose(
[
AddGaussianNoise(min_amplitude=0.001, max_amplitude=0.015, p=1),
TimeStretch(min_rate=0.8, max_rate=1.25, p=1),
PitchShift(min_semitones=-4, max_semitones=4, p=1),
]
)
augmented_data = augment(data, sample_rate=sr)
display(Audio(augmented_data, rate=sr))
Посмотрим на то, что получилось:
produce_plots(data, augmented_data, sr)
Дополнительные библиотеки для аугментации звука (и волновых функций в целом):
Теперь рассмотрим несколько примеров аугментаций текста. С полным списком можно ознакомиться здесь: nlpaug 🐾[git].
!pip install -q nlpaug
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 410.5/410.5 kB 9.1 MB/s eta 0:00:00
# Define input text
text = "Hello, future of AI for Science! How are you today?"
print(f"input text: {text}")
input text: Hello, future of AI for Science! How are you today?
Заменой на похоже выглядящие:
import nlpaug.augmenter.char as nac
augment = nac.OcrAug()
augmented_text = augment.augment(text)
print(f"Original:\n{text}")
print(f"Augmented Texts:\n{augmented_text}")
Original: Hello, future of AI for Science! How are you today? Augmented Texts: ['Hello, future uf AI for Science! H0w are y0o tuday?']
С опечатками, которые учитывают расположение символов на клавиатуре:
augment = nac.KeyboardAug()
augmented_text = augment.augment(text)
print(f"Original:\n{text}")
print(f"Augmented Texts:\n{augmented_text}")
Original: Hello, future of AI for Science! How are you today? Augmented Texts: ['melPo, fu%uge of AI for DciSmce! How are you tkFay?']
С орфографическими ошибками:
import nlpaug.augmenter.word as naw
augment = naw.SpellingAug()
augmented_text = augment.augment(text, n=3)
print(f"Original:\n{text}")
print(f"Augmented Texts:\n{augmented_text}")
Original: Hello, future of AI for Science! How are you today? Augmented Texts: ['Hllo, future or AI dor Science! How arre you today?', 'Hello, future of AI fom Sciece! Gow ares you today?', 'Hello, future of AI fot Sciens! Yow ard you today?']
С использованием модели для предсказания новых слов в зависимости от контекста:
from IPython.display import clear_output
# model_type: word2vec, glove or fasttext
augment = naw.ContextualWordEmbsAug(model_path="bert-base-uncased", action="insert")
augmented_text = augment.augment(text)
clear_output()
print(f"Original:\n{text}")
print(f"Augmented Texts:\n{augmented_text}")
Original: Hello, future of AI for Science! How are you today? Augmented Texts: ['hello, future ceo of electronic ai for science! how important are you with today?']
Мы можем перевести текстовые данные на какой-либо язык, а затем перевести их обратно на язык оригинала. Это может помочь сгенерировать текстовые данные с разными словами, сохраняя при этом контекст текстовых данных.
!pip install -q sacremoses
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 897.5/897.5 kB 16.7 MB/s eta 0:00:00
back_translation_aug = naw.BackTranslationAug(
from_model_name="facebook/wmt19-en-de", to_model_name="facebook/wmt19-de-en"
)
augmented_text = back_translation_aug.augment(text)
clear_output()
print(f"Original:\n{text}")
print(f"Augmented Texts:\n{augmented_text}")
Original: Hello, future of AI for Science! How are you today? Augmented Texts: ['Hello, the future of AI for science! How are you doing today?']
Instance Crossover Augmentation — составление новых объектов класса из отдельных предложений того же класса. Например, есть два объекта одного класса "положительный отзыв":
Тогда можно составить новый объект того же класса из их частей:
Важно: при любых аугментациях текста на уровне предложений есть шанс создать странные и нелогичные объекты, поэтому использовать их следует с особой осторожностью.
Дополнительные библиотеки для аугментации текста:
Глобально метрики качества машинного перевода можно подразделить на традиционные и нейросетевые.
Традиционные метрики сравнительно просты в расчете и прозрачны, наиболее известные из них разработаны до бума нейросетей. Чаще всего такие метрики основаны на подсчете числа совпадений символов / слов / cловосочетаний – их называют «lexic overlap metrics».
Большинство метрик, предложенных после 2016 года – нейросетевые. Первым шагом в применении нейросетей в расчете метрик стало использование векторных представлений слов (embeddings).
Сегодня наиболее используемые – метрики, предложенные до 2010 года, причем в 99% это BLEU.
Наиболее известны и употребимы такие традиционные метрики как: BLEU, NIST, ROUGE, METEOR, TER, chrF, chrF++, RIBES.
BLEU
BLEU (BiLingual Evaluation Understudy) — метрика, разработанная в IBM (Papineni et al.) в 2001. Основана на подсчете слов (unigrams) и словосочетаний (n‑grams) из машинного перевода, также встречающихся в эталоне. Далее это число делится на общее число слов и словосочетаний в машинном переводе — получается precision. К итоговому precision применяется корректировка — штраф за краткость (brevity penalty), чтобы избежать слишком высоких оценок BLEU для кратких и неполных переводов.
from torchtext.data.metrics import bleu_score
candidate_corpus = [["My", "full", "pytorch", "test"], ["Another", "Sentence"]]
references_corpus = [
[["My", "full", "pytorch", "test"], ["Completely", "Different"]],
[["No", "Match"]],
]
print(bleu_score(candidate_corpus, references_corpus))
0.8408964276313782
Попробуем решить задачу sequence-to-sequence: преобразование последовательности $X$ длины $N$ в последовательность $Y$ длины $T$. $T$ может быть не равно $N$.
Примеры sequence-to-sequence задач:
Для решения таких задач можно использовать две RNN: кодировщик и декодировщик.
В качестве вектора $C$ можно использовать последнее скрытое состояние кодировщика $h_N$.
Таким образом:
Кодировщик на основании входной последовательности предсказывает нулевое скрытое состояние декодировщика и вектор контекста $\large с$, который часто равен финальному скрытому состоянию кодировщика.
Кодировщик: $\large h_i = f_w(x_i, h_{i_1})$
Декодировщик: $\large s_t = g_u(y_{t-1}, s_{t-1}, c)$
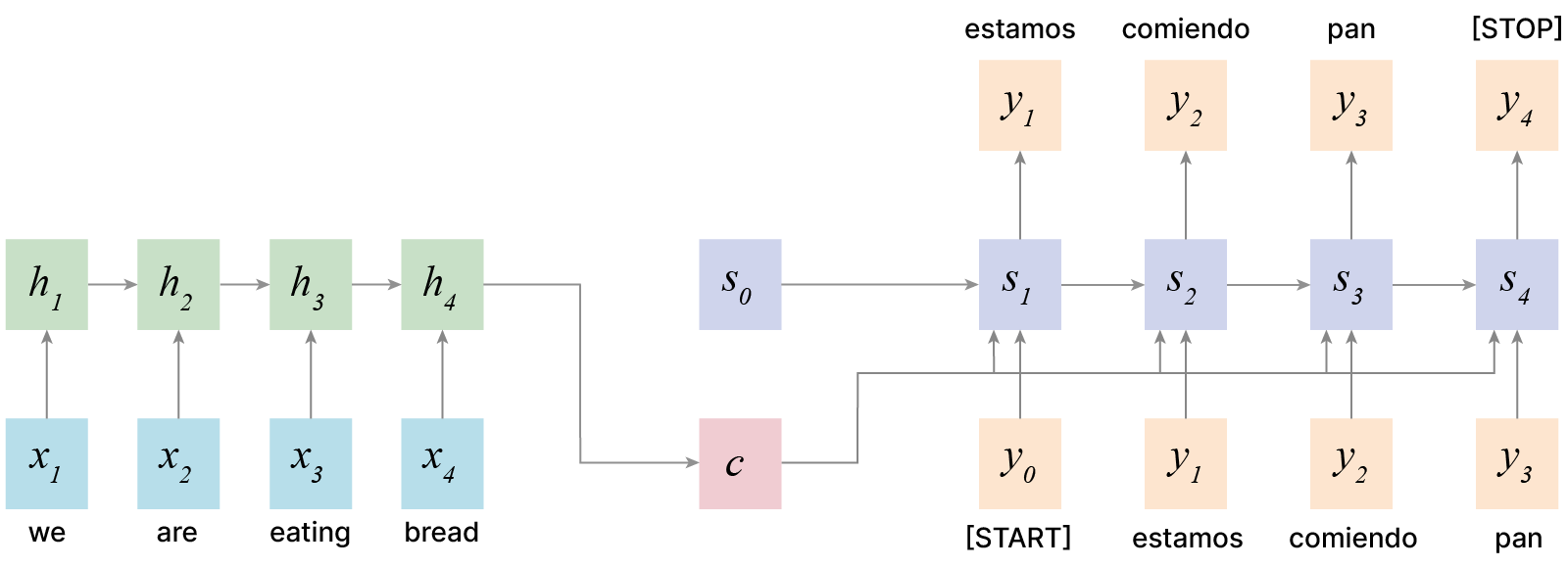
При этом возникает следующая проблема: мы пропускаем информацию из входной последовательности через бутылочное горлышко — вектор фиксированного размера $h_N$. Что будет, если размер последовательности 1000?
Идея: использовать новый вектор контекста на каждом шаге.
В данном подходе мы используем один вектор контекста фиксированной длины $c$, в который собираем информацию со всей входной последовательности $(x_1,...,x_N)$.
Входная последовательность может содержать как единицы, так и тысячи элементов. В задаче машинного перевода входной последовательностью может быть:
Контекст важен. Для генерации глагола в правильной форме нужно понимать, к какому существительному он относится, а для качественного перевода конца абзаца необходимо понимать, о чем шла речь в его начале.
Проблемы Sequence-to-Sequence
При этом возникают проблемы:
Вектор контекста $c$ и скрытые состояния декодировщика $s_t$ являются “бутылочными горлышками” модели.
SOS_token = 0
EOS_token = 1
class Lang:
def __init__(self, name):
self.name = name
self.word2index = {}
self.word2count = {}
self.index2word = {0: "SOS", 1: "EOS"}
self.n_words = 2 # Count SOS and EOS
def addSentence(self, sentence):
for word in sentence.split(" "):
self.addWord(word)
def addWord(self, word):
if word not in self.word2index:
self.word2index[word] = self.n_words
self.word2count[word] = 1
self.index2word[self.n_words] = word
self.n_words += 1
else:
self.word2count[word] += 1
Все файлы представлены в формате Unicode, поэтому для упрощения мы преобразуем символы Unicode в ASCII, сделаем все строчными и уберём большую часть знаков препинания.
import re
import unicodedata
def unicodeToAscii(s):
return "".join(
c for c in unicodedata.normalize("NFD", s) if unicodedata.category(c) != "Mn"
)
def normalizeString(s):
s = unicodeToAscii(s.lower().strip())
s = re.sub(r"([.!?])", r" \1", s)
s = re.sub(r"[^a-zA-Z!?]+", r" ", s)
return s.strip()
def normalizeStringRu(s):
s = unicodeToAscii(s.lower().strip())
s = re.sub(r"([.!?])", r" \1", s)
s = re.sub(r"[^a-яА-Я!?]+", r" ", s)
return s.strip()
Зафиксируем seeds для воспроизводимости результата:
import torch
import random
import numpy as np
def set_random_seed(seed):
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
np.random.seed(seed)
random.seed(seed)
set_random_seed(42)
Делим файл на строки, а строки — на пары.
# Source: https://www.manythings.org/anki/
!wget -q https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/eng_rus_vocab.txt
from io import open
def readLangs(lang1, lang2, reverse=False):
print("Reading lines...")
# Read the file and split into lines
lines = (
open("%s_%s_vocab.txt" % (lang1, lang2), encoding="utf-8")
.read()
.strip()
.split("\n")
)
# Split every line into pairs and normalize
pairs = [l.split("\t")[:2] for l in lines]
eng = [normalizeString(s[0]) for s in pairs]
rus = [normalizeStringRu(s[1]) for s in pairs]
pairs = list(zip(rus, eng))
# Reverse pairs, make Lang instances
if reverse:
pairs = [list(reversed(p)) for p in pairs]
input_lang = Lang(lang2)
output_lang = Lang(lang1)
else:
input_lang = Lang(lang1)
output_lang = Lang(lang2)
return input_lang, output_lang, pairs
Для скорости сократим датасет до предложений не длинее 10 слов и отфильтруем апострофы.
max_length = 10
eng_prefixes = (
"i am ",
"i m ",
"he is",
"he s ",
"she is",
"she s ",
"you are",
"you re ",
"we are",
"we re ",
"they are",
"they re ",
)
def filterPair(p):
return (
len(p[0].split(" ")) < max_length
and len(p[1].split(" ")) < max_length
and p[1].startswith(eng_prefixes)
)
def filterPairs(pairs):
return [pair for pair in pairs if filterPair(pair)]
import random
def prepareData(lang1, lang2, reverse=False):
input_lang, output_lang, pairs = readLangs(lang1, lang2, reverse)
print("Read %s sentence pairs" % len(pairs))
pairs = filterPairs(pairs)
print("Trimmed to %s sentence pairs" % len(pairs))
print("Counting words...")
for pair in pairs:
input_lang.addSentence(pair[0])
output_lang.addSentence(pair[1])
print("Counted words:")
print(input_lang.name, input_lang.n_words)
print(output_lang.name, output_lang.n_words)
return input_lang, output_lang, pairs
input_lang, output_lang, pairs = prepareData("eng", "rus", False)
print(random.choice(pairs))
Reading lines...
Read 496059 sentence pairs
Trimmed to 30724 sentence pairs
Counting words...
Counted words:
eng 10510
rus 4349
('простите что была так груба', 'i m sorry that i was so rude')
import torch
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
def indexesFromSentence(lang, sentence):
return [lang.word2index[word] for word in sentence.split(" ")]
def tensorFromSentence(lang, sentence):
indexes = indexesFromSentence(lang, sentence)
indexes.append(EOS_token)
return torch.tensor(indexes, dtype=torch.long, device=device).view(1, -1)
def tensorsFromPair(pair):
input_tensor = tensorFromSentence(input_lang, pair[0])
target_tensor = tensorFromSentence(output_lang, pair[1])
return (input_tensor, target_tensor)
Теперь в нашем распоряжении есть два словаря и набор пар строк. Определим структуру модели.
from torch import nn
class EncoderRNN(nn.Module):
def __init__(self, input_size, hidden_size, dropout_p=0.1):
super(EncoderRNN, self).__init__()
self.hidden_size = hidden_size
self.embedding = nn.Embedding(input_size, hidden_size)
self.gru = nn.GRU(hidden_size, hidden_size, batch_first=True)
self.dropout = nn.Dropout(dropout_p)
def forward(self, input):
embedded = self.dropout(self.embedding(input))
output, hidden = self.gru(embedded)
return output, hidden
Вместо one_hot-векторов, используются эмбеддинги 🛠️[doc] размером 1×256 (hidden size)
import torch.nn.functional as F
class DecoderRNN(nn.Module):
def __init__(self, hidden_size, output_size):
super(DecoderRNN, self).__init__()
self.embedding = nn.Embedding(output_size, hidden_size)
self.gru = nn.GRU(hidden_size, hidden_size, batch_first=True)
self.out = nn.Linear(hidden_size, output_size)
def forward(self, encoder_outputs, encoder_hidden, target_tensor=None):
batch_size = encoder_outputs.size(0)
decoder_input = torch.empty(
batch_size, 1, dtype=torch.long, device=device
).fill_(SOS_token)
decoder_hidden = encoder_hidden
decoder_outputs = []
for i in range(max_length):
decoder_output, decoder_hidden = self.forward_step(
decoder_input, decoder_hidden, encoder_outputs
)
decoder_outputs.append(decoder_output)
if target_tensor is not None:
# Teacher forcing: Feed the target as the next input
decoder_input = target_tensor[:, i].unsqueeze(1) # Teacher forcing
else:
# Without teacher forcing: use its own predictions as the next input
_, topi = decoder_output.topk(1)
decoder_input = topi.squeeze(
-1
).detach() # detach from history as input
decoder_outputs = torch.cat(decoder_outputs, dim=1)
decoder_outputs = F.log_softmax(decoder_outputs, dim=-1)
return (
decoder_outputs,
decoder_hidden,
None,
) # We return `None` for consistency in the training loop
def forward_step(self, input, hidden, encoder_outputs):
output = self.embedding(input)
output = F.relu(output)
output, hidden = self.gru(output, hidden)
output = self.out(output)
return output, hidden
На вход модели будем подавать индексы слов для первой части пары из одного словаря, а на выходе ожидать индексы для соответствующей пары из другого.
import numpy as np
from torch.utils.data import TensorDataset, DataLoader, RandomSampler
def get_dataloader(batch_size):
input_lang, output_lang, pairs = prepareData("eng", "rus", False)
n = len(pairs)
input_ids = np.zeros((n, max_length), dtype=np.int32)
target_ids = np.zeros((n, max_length), dtype=np.int32)
for idx, (inp, tgt) in enumerate(pairs):
inp_ids = indexesFromSentence(input_lang, inp)
tgt_ids = indexesFromSentence(output_lang, tgt)
inp_ids.append(EOS_token)
tgt_ids.append(EOS_token)
input_ids[idx, : len(inp_ids)] = inp_ids
target_ids[idx, : len(tgt_ids)] = tgt_ids
train_data = TensorDataset(
torch.LongTensor(input_ids).to(device), torch.LongTensor(target_ids).to(device)
)
train_sampler = RandomSampler(train_data)
train_dataloader = DataLoader(
train_data, sampler=train_sampler, batch_size=batch_size
)
return input_lang, output_lang, train_dataloader
def train_epoch(
dataloader, encoder, decoder, encoder_optimizer, decoder_optimizer, criterion
):
total_loss = 0
for data in dataloader:
input_tensor, target_tensor = data
encoder_optimizer.zero_grad()
decoder_optimizer.zero_grad()
encoder_outputs, encoder_hidden = encoder(input_tensor)
decoder_outputs, _, _ = decoder(encoder_outputs, encoder_hidden, target_tensor)
loss = criterion(
decoder_outputs.view(-1, decoder_outputs.size(-1)), target_tensor.view(-1)
)
loss.backward()
encoder_optimizer.step()
decoder_optimizer.step()
total_loss += loss.item()
return total_loss / len(dataloader)
import time
import math
def asMinutes(s):
m = math.floor(s / 60)
s -= m * 60
return "%dm %ds" % (m, s)
def timeSince(since, percent):
now = time.time()
s = now - since
es = s / (percent)
rs = es - s
return "%s (- %s)" % (asMinutes(s), asMinutes(rs))
from torch import optim
def train(
train_dataloader,
encoder,
decoder,
num_epochs,
learning_rate=0.001,
print_every=100,
plot_every=100,
):
start = time.time()
plot_losses = []
print_loss_total = 0 # Reset every print_every
plot_loss_total = 0 # Reset every plot_every
encoder_optimizer = optim.Adam(encoder.parameters(), lr=learning_rate)
decoder_optimizer = optim.Adam(decoder.parameters(), lr=learning_rate)
criterion = nn.NLLLoss()
for epoch in range(1, num_epochs + 1):
loss = train_epoch(
train_dataloader,
encoder,
decoder,
encoder_optimizer,
decoder_optimizer,
criterion,
)
print_loss_total += loss
plot_loss_total += loss
if epoch % print_every == 0:
print_loss_avg = print_loss_total / print_every
print_loss_total = 0
print(
"%s (%d %d%%) %.4f"
% (
timeSince(start, epoch / num_epochs),
epoch,
epoch / num_epochs * 100,
print_loss_avg,
)
)
if epoch % plot_every == 0:
plot_loss_avg = plot_loss_total / plot_every
plot_losses.append(plot_loss_avg)
plot_loss_total = 0
showPlot(plot_losses)
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
%matplotlib inline
plt.switch_backend("agg")
def showPlot(points):
plt.figure()
fig, ax = plt.subplots()
# this locator puts ticks at regular intervals
loc = ticker.MultipleLocator(base=0.2)
ax.yaxis.set_major_locator(loc)
plt.plot(points)
plt.show()
Процесс обучения занимает примерно 15 минут. Для запуска обучения необходимо раскомментировать соответствующую строчку в коде.
hidden_size = 128
batch_size = 32
input_lang, output_lang, train_dataloader = get_dataloader(batch_size)
encoder = EncoderRNN(input_lang.n_words, hidden_size).to(device)
decoder = DecoderRNN(hidden_size, output_lang.n_words).to(device)
# train(train_dataloader, encoder, decoder, num_epochs=80, print_every=5, plot_every=5)
Reading lines... Read 496059 sentence pairs Trimmed to 30724 sentence pairs Counting words... Counted words: eng 10510 rus 4349
Загрузим заранее обученные веса энкодера и декодера:
!wget -q https://edunet.kea.su/repo/EduNet-content/dev-2.0/L09/weights/encoder_weights.pth
!wget -q https://edunet.kea.su/repo/EduNet-content/dev-2.0/L09/weights/decoder_weights.pth
encoder.load_state_dict(torch.load("/content/encoder_weights.pth", map_location=device))
decoder.load_state_dict(torch.load("/content/decoder_weights.pth", map_location=device))
<All keys matched successfully>
Тестирование
def evaluate(encoder, decoder, sentence, input_lang, output_lang):
with torch.no_grad():
input_tensor = tensorFromSentence(input_lang, sentence)
encoder_outputs, encoder_hidden = encoder(input_tensor)
decoder_outputs, decoder_hidden, _ = decoder(encoder_outputs, encoder_hidden)
_, topi = decoder_outputs.topk(1)
decoded_ids = topi.squeeze()
decoded_words = []
for idx in decoded_ids:
if idx.item() == EOS_token:
decoded_words.append("<EOS>")
break
decoded_words.append(output_lang.index2word[idx.item()])
return decoded_words
Мы можем оценить случайные предложения из обучающего набора:
def evaluateRandomly(encoder, decoder, n=10):
for i in range(n):
pair = random.choice(pairs)
print("RUS", pair[0])
print("ENG", pair[1])
output_words = evaluate(encoder, decoder, pair[0], input_lang, output_lang)
output_sentence = " ".join(output_words)
print("DNN", output_sentence)
print("")
encoder.eval()
decoder.eval()
evaluateRandomly(encoder, decoder)
RUS я не совсем уверен ENG i m not so sure DNN i m not totally sure are work <EOS> RUS я доволен ENG i m pleased DNN i m satisfied with the dog <EOS> RUS я никуда с тобои не поеду ENG i m not going anywhere with you DNN i m not going anywhere with you <EOS> RUS я привык ждать ENG i m used to waiting DNN i m used to doing that <EOS> RUS вы оба симпатичные ENG you re both pretty DNN you re both pretty young <EOS> RUS я всего лишь учитель ENG i m just a teacher DNN i m just a teacher <EOS> RUS я переводчица ENG i m a translator DNN i m a member of the team <EOS> RUS в настоящии момент я работаю в бостоне ENG i m currently working in boston DNN i m currently working in boston <EOS> RUS я смертельно устал ENG i am dead tired DNN i am very tired from swimming <EOS> RUS уверен что том тебя не ненавидит ENG i m sure tom doesn t hate you DNN i m sure tom doesn t hate you <EOS>
Литература
Особенности данных:
Рекуррентные нейронные сети:
LSTM:
Пример посимвольной генерации текста:
Представление данных:
Аугментация:
NLP метрики: