Сверточные нейронные сети
Fully-connected Neural Network (FCN). В современных статьях чаще используется термин Multi-Layer Perceptron (MLP).
На прошлом занятии мы научились строить сети из нескольких слоев.
Вспомним, что нам необходимо для этого сделать:
Примечание: Для цветного изображения из CIFAR-10 размером $32\times32$ пикселя ($32\times32\times3$) размерность входного вектора будет равна $3072$.
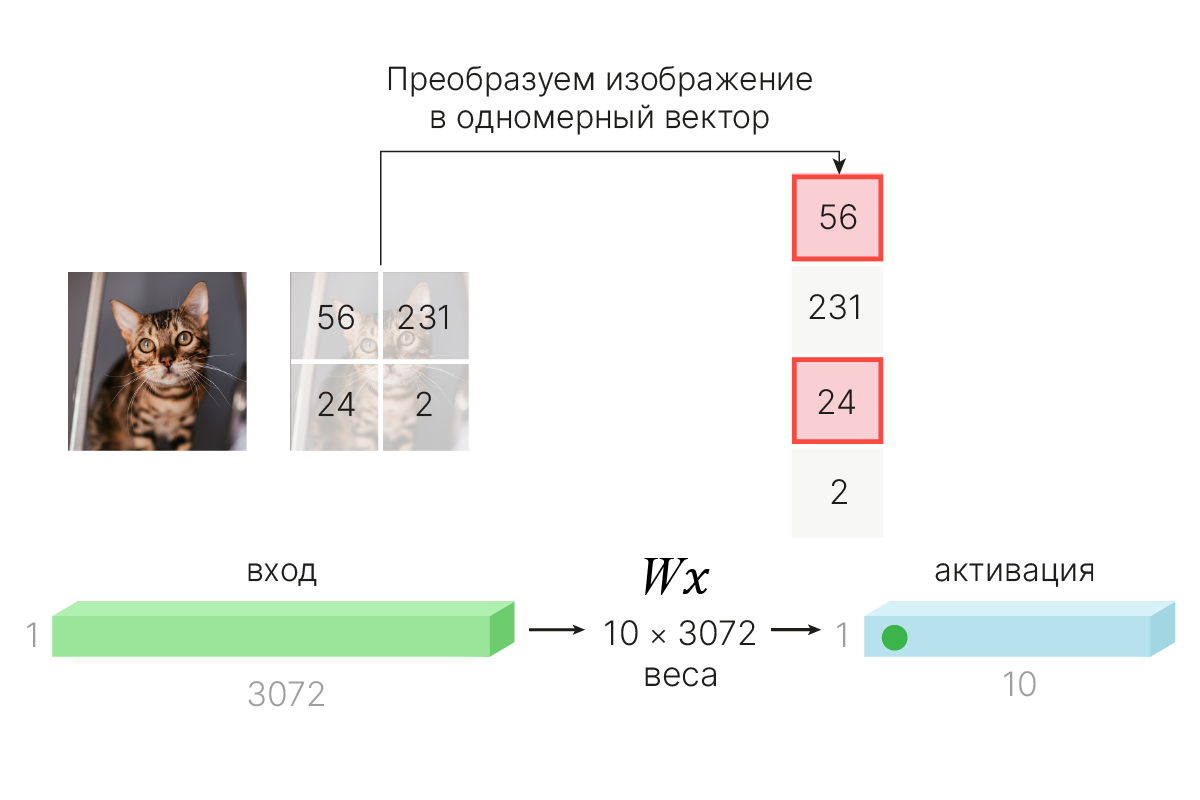
Перемножаем матрицу данных с матрицей весов. Размер последней может быть, например, $100\times3072$, где $3072$ — размер входного вектора, а $100$ — количество признаков, которое мы хотим получить. Результат обработки одного входа будет иметь размер $100\times1$.
Поэлементно применяем к вектору признаков нелинейную функцию (функцию активации), например, Sigmoid или ReLU. Размерность данных при этом не меняется ($100\times1$). В результате получаем вектор активаций.
Используем полученные активации как входные данные для нового слоя. Количество весов слоя будет зависеть от размерности входной матрицы и того, что мы хотим получить на выходе. Если мы делаем классификатор на $10$ классов, то матрица весов должна иметь размерность $10\times100$, и на этом можно остановиться. Но в общем случае количество слоев может быть произвольным.
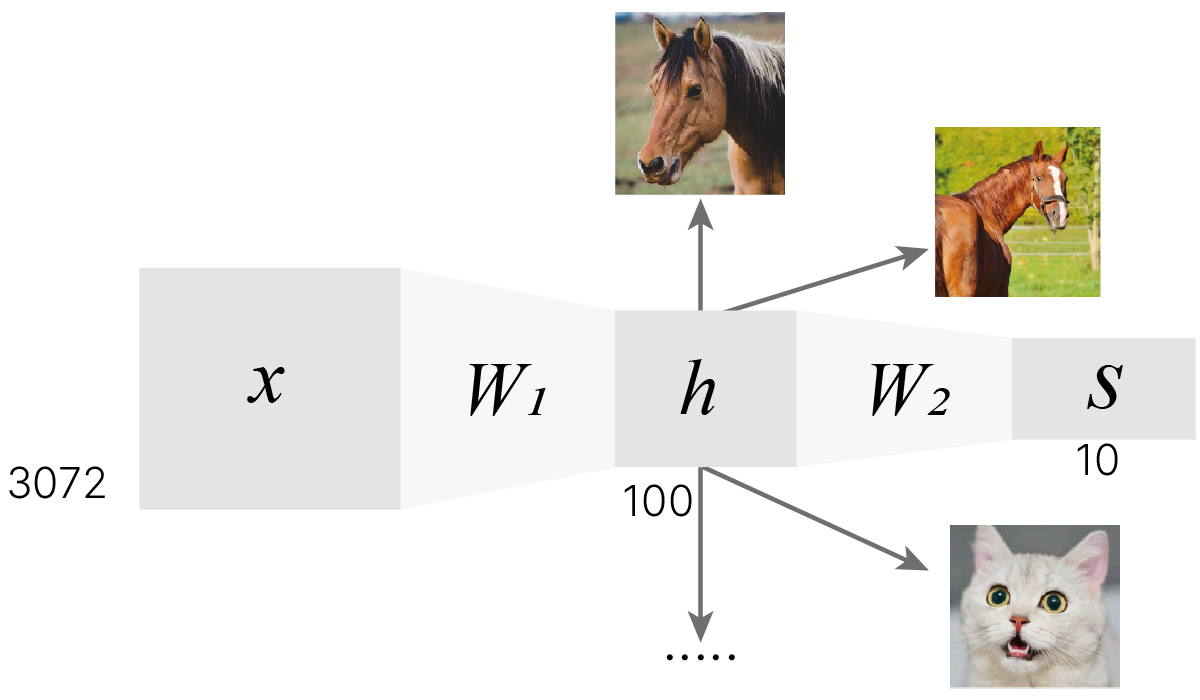
$\large h=W_1 \cdot x$
$\large S=W_2 \cdot f(h)=W_2 \cdot f(W_1 \cdot x)$
На изображении представлена описанная выше нейронная сеть. Добавление второго слоя позволило модели использовать более одного шаблона на класс. Можно убедиться в этом, обучив модель на датасете CIFAR-10 и визуализировав веса первого слоя модели.
from torch import nn
class FCNet(nn.Module):
def __init__(self):
super().__init__()
self.layers_stack = nn.Sequential(
nn.Linear(3 * 32 * 32, 64),
nn.ReLU(),
nn.Linear(64, 10),
)
def forward(self, x):
return self.layers_stack(x)
Скачаем файл с предобученными весами (точность $\approx0.5$)
!wget -q "https://edunet.kea.su/repo/EduNet-web_dependencies/weights/2layer.pt"
Загрузим веса в модель:
import torch
fc_model = FCNet()
weights_in_dict = torch.load("2layer.pt")
fc_model.load_state_dict(weights_in_dict)
<All keys matched successfully>
MLP: Набор шаблонов классов, выученных нейросетью.
Визуализируем веса первого слоя:
import matplotlib.pyplot as plt
from torchvision import utils
W1 = fc_model.layers_stack[0].weight.reshape(64, 3, 32, 32) # layer has 64 neurons
img_grid = utils.make_grid(W1, pad_value=1, normalize=True, nrow=16)
plt.figure(figsize=(20, 12))
plt.title("Weights visualization in 2D")
plt.imshow(img_grid.permute(1, 2, 0).cpu().numpy()) # CHW -> HWC
plt.axis("off")
plt.show()
За счёт создания нескольких шаблонов для каждого из классов многослойные архитектуры в общем случае показывают более высокую эффективность на задачах классификации изображений. Однако и здесь есть что улучшить.
При вытягивании изображения в вектор мы теряем информацию о взаимном расположении пикселей на исходной картинке.
!wget -q "https://edunet.kea.su/repo/EduNet-web_dependencies/dev-2.0/L06/digit.png"
import numpy as np
from PIL import Image
image = Image.open("digit.png")
img_np = np.array(image)
plt.imshow(img_np, cmap="gray")
plt.show()
print(img_np)
[[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 12 15 20 12 1 0 0 0] [ 0 0 0 0 0 0 3 123 225 242 255 225 137 7 0 0] [ 0 0 0 0 0 15 207 251 103 109 107 105 171 145 0 0] [ 0 0 0 0 0 149 236 80 0 0 0 0 4 21 0 0] [ 0 0 0 0 16 228 106 0 17 33 17 0 0 0 0 0] [ 0 0 0 0 97 248 98 138 232 255 216 22 0 0 0 0] [ 0 0 0 0 50 247 255 197 111 123 252 129 0 0 0 0] [ 0 0 0 0 1 54 55 9 0 49 250 116 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 158 240 44 0 0 0 0] [ 0 0 0 0 0 0 0 0 88 255 125 0 0 0 0 0] [ 0 0 0 0 7 15 23 132 255 188 12 0 0 0 0 0] [ 0 0 0 0 20 200 229 240 157 28 0 0 0 0 0 0] [ 0 0 0 0 3 64 73 45 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]
fig, ax = plt.subplots(ncols=2, figsize=(10, 4))
ax[0].imshow(img_np, cmap="gray")
ax[1].imshow(img_np.reshape(1, -1), aspect=20, cmap="gray")
ax[0].set_title("Original image")
ax[1].set_title("Flattened image")
vector = np.array(image).flatten()
print(list(vector))
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 12, 15, 20, 12, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3, 123, 225, 242, 255, 225, 137, 7, 0, 0, 0, 0, 0, 0, 0, 15, 207, 251, 103, 109, 107, 105, 171, 145, 0, 0, 0, 0, 0, 0, 0, 149, 236, 80, 0, 0, 0, 0, 4, 21, 0, 0, 0, 0, 0, 0, 16, 228, 106, 0, 17, 33, 17, 0, 0, 0, 0, 0, 0, 0, 0, 0, 97, 248, 98, 138, 232, 255, 216, 22, 0, 0, 0, 0, 0, 0, 0, 0, 50, 247, 255, 197, 111, 123, 252, 129, 0, 0, 0, 0, 0, 0, 0, 0, 1, 54, 55, 9, 0, 49, 250, 116, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 158, 240, 44, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 88, 255, 125, 0, 0, 0, 0, 0, 0, 0, 0, 0, 7, 15, 23, 132, 255, 188, 12, 0, 0, 0, 0, 0, 0, 0, 0, 0, 20, 200, 229, 240, 157, 28, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3, 64, 73, 45, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Пиксели, которые были соседними и составляли цельный объект, могут оказаться на большом расстоянии внутри результирующего вектора. Получается, что мы просто удалили информацию об их близости, важность которой нам как людям очевидна.
Идея полносвязной нейронной сети пришла к нам из математической модели восприятия информации мозгом (перцептрон Розенблатта ✏️[blog]). Возможно, чтобы получить хорошие результаты при обработке изображений, нужно посмотреть, как работает человеческий глаз?
В полносвязной сети каждый нейрон "видит" сразу все изображение (все данные). Наша зрительная система работает иначе.
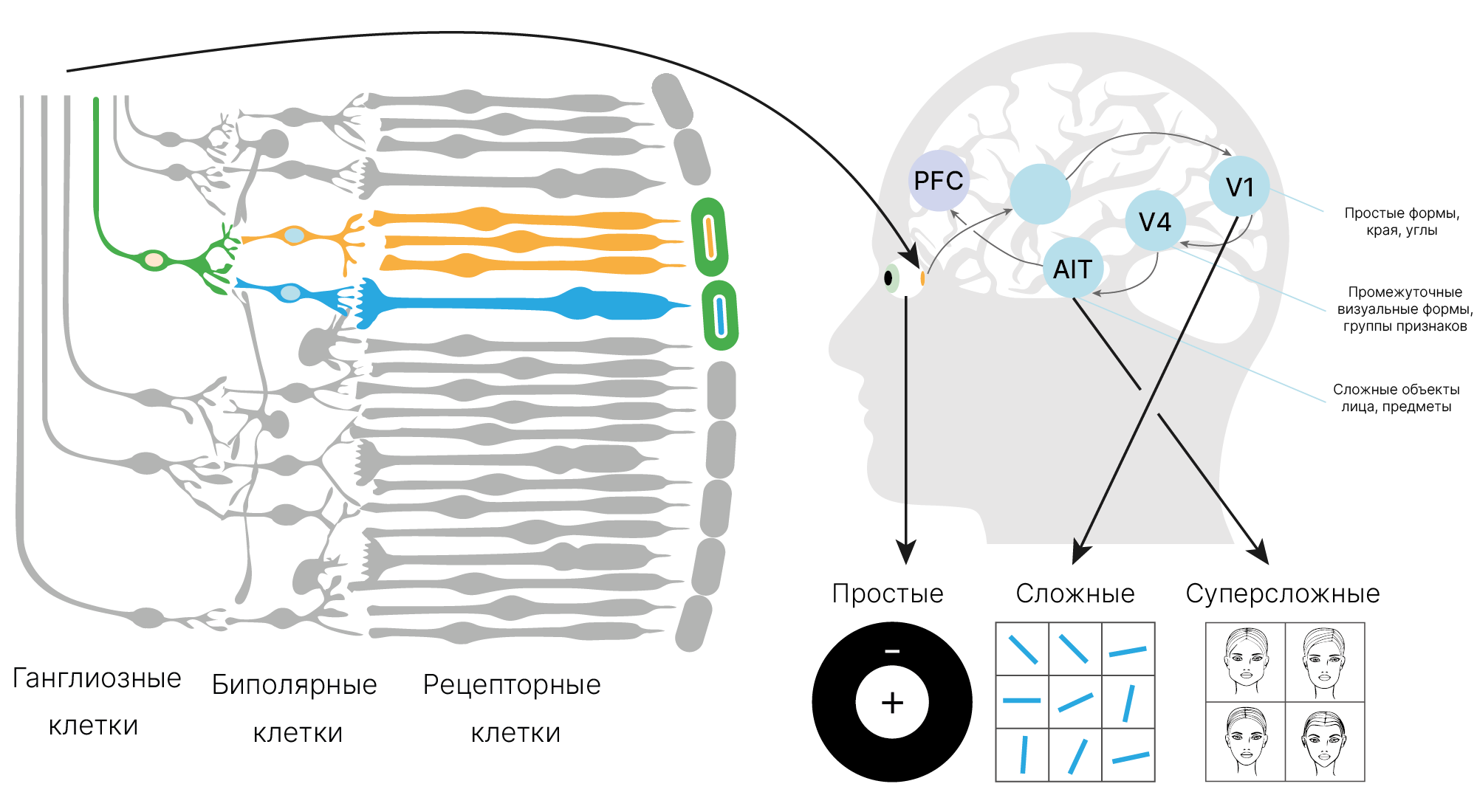
Каждый фоторецептор на сетчатке нашего глаза (палочка или колбочка) реагирует только на свет, попавший на него.
Сигнал от фоторецептора попадает на нейрон следующего уровня (биполярная клетка 📚[wiki]). Этот нейрон уже соединен с несколькими фоторецепторами. Область, в которой они локализованы, называется рецептивным полем. Нейрон возбуждается при определенной комбинации сигналов от связанных с ним рецепторных клеток. По сути, он реагирует на простой, локально расположенный паттерн.
Клетки уровнем выше (ганглиозные) собирают информацию с нескольких близко расположенных биполярных клеток и активируются при уникальной комбинации сигналов с них. Их рецептивное поле больше, и паттерны, на которые они реагируют, сложнее.
Рецептивное поле нейрона — это участок с рецепторами, с которых он прямо или опосредованно, через другие нейроны, получает информацию.
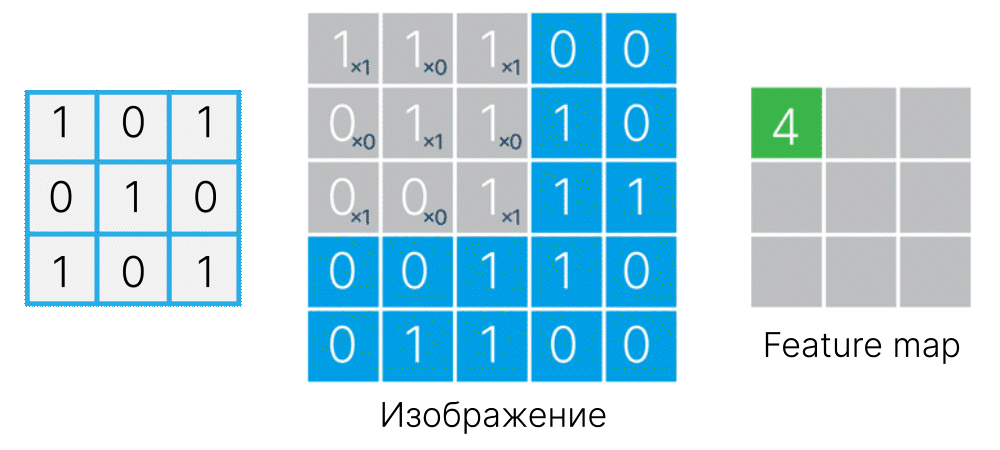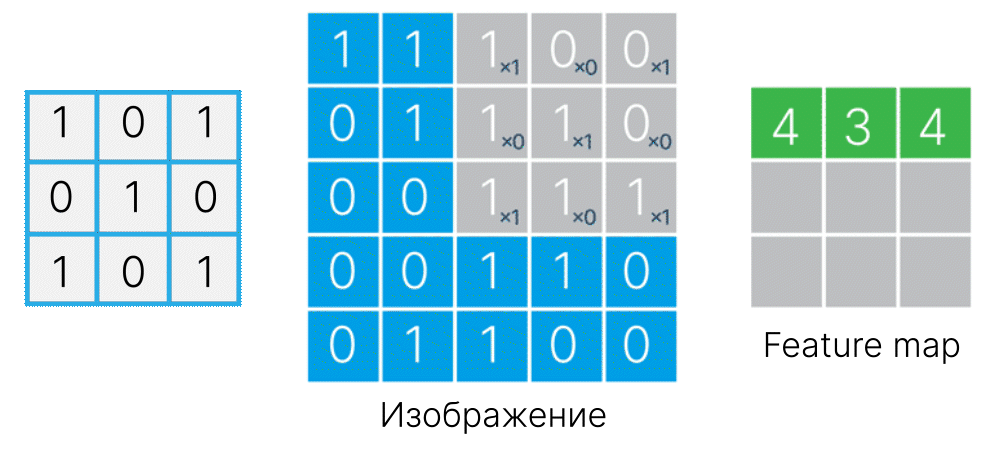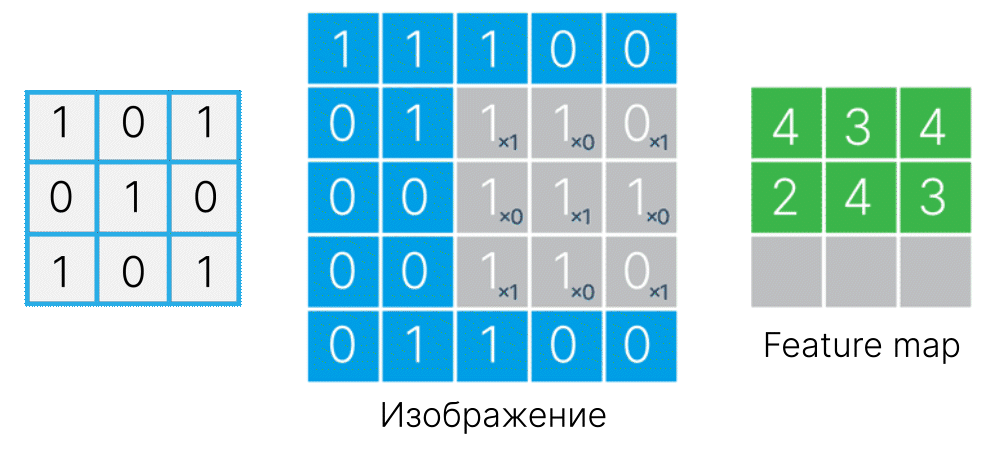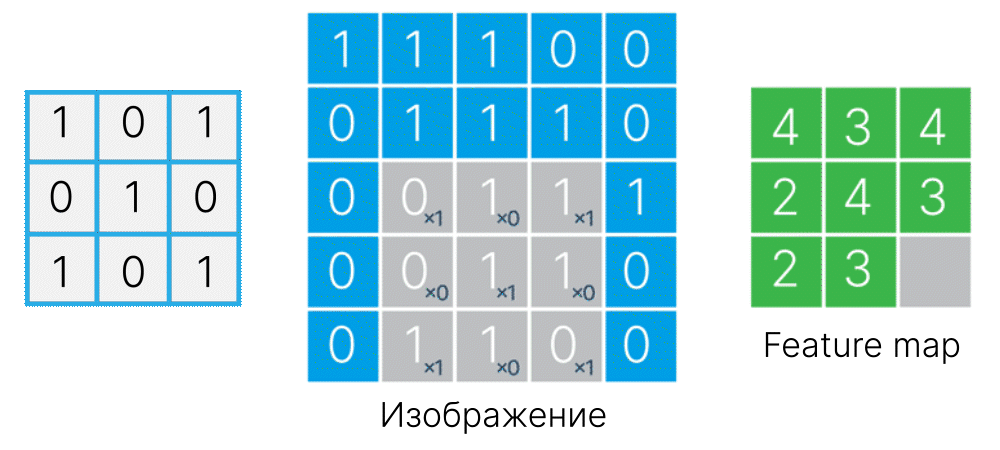
Получается, что можно не подавать на вход нейрона первого слоя информацию о всем изображении сразу, а "показать" ему только часть картинки, чтобы он научился распознавать простые, но универсальные паттерны. А их агрегация произойдет в последующих слоях.
Для этого используется так называемое "скользящее окно", которое двигается по изображению, захватывая на каждом шаге только небольшую область.
Такой подход используют, например, при наложении графических фильтров. Вы наверняка пользовались ими, если работали в графических редакторах, например, в Photoshop.
Простейший фильтр — это Box blur 📚[wiki], который просто усредняет значения соседних пикселей.
from skimage import data, color
from skimage.transform import rescale
# fmt: off
box_blur_kernel = 1/9 * np.array([[1, 1, 1],
[1, 1, 1],
[1, 1, 1]])
# fmt: on
def apply_filter(img, kernel):
h, w = np.array(img.shape) # image height and width
kh, kw = np.array(kernel.shape) # kernel height and width (3x3)
# calculate the output size, hard work ...
out = np.zeros((h - kh + 1, w - kw + 1))
for i in range(h - kh + 1):
for j in range(w - kw + 1):
# get 3x3 patch from image
patch = img[i : i + kh, j : j + kw]
# elementwise multiply patch pixels to kernel weights and sum
new_pixel = np.multiply(patch, kernel).sum()
# store modified pixel in new blurred image
out[i, j] = new_pixel
return out
def show(img, result):
# Display results
fig, axes = plt.subplots(1, 2, figsize=(15, 5))
axes[0].imshow(img, cmap="gray")
axes[1].imshow(out, cmap="gray")
axes[0].set(title=f"Original image, shape: {img_cat_resc.shape}")
axes[1].set(title=f"Blurred image: {out.shape}")
axes[0].axis("off")
axes[1].axis("off")
plt.show()
img_cat = color.rgb2gray(data.cat())
img_cat_resc = rescale(img_cat, 0.25, anti_aliasing=False) * 255
out = apply_filter(img_cat_resc, box_blur_kernel)
show(img_cat_resc, out)
Можно умножать каждый пиксель на свой коэффициент. Так устроен, например, фильтр Гаусса 📚[wiki].
Реализуем фильтр Гаусса размером $3\times3$ для размытия изображения:
# fmt: off
# Gaussian 3x3 kernel, sum of weights == 1
gauss_kernel = np.array([[1/16, 1/8, 1/16],
[1/8, 1/4, 1/8 ],
[1/16, 1/8, 1/16]])
# fmt: on
out = apply_filter(img_cat_resc, gauss_kernel)
show(img_cat_resc, out)
Последовательность действий:
Таким образом, для получения нового изображения мы применили формулу:
$$\large \text{output}(x,y) = \sum_{i}^{H} \sum_{j}^{W}k[i,j] I[x+j,y+i],$$где $H, W$ — высота и ширина ядра фильтра, $I$ — исходное изображение.
Если бы мы вытянули фрагменты картинки и ядро фильтра в вектора, а затем их скалярно перемножили, результат был бы тем же!
Такой же алгоритм можно применять не для сглаживания изображения, а для поиска (выделения) на нем чего-либо (например, контуров объектов). Для этого достаточно заменить ядро фильтра.
# fmt: off
sobel_y_kernel = torch.tensor([[ 1.0, 2.0, 1.0 ],
[ 0.0, 0.0, 0.0 ],
[-1.0, -2.0, -1.0]])
# fmt: on
x_edges = apply_filter(img_cat * 255, sobel_y_kernel)
fig, axes = plt.subplots(1, 2, figsize=(15, 5))
axes[0].imshow(img_cat, cmap="gray")
axes[1].imshow(x_edges, cmap="gray", vmin=0, vmax=255)
axes[0].set(title=f"Original image, shape: {img_cat.shape}")
axes[1].set(title=f"Horizontal edges detector: {x_edges.shape}")
axes[0].axis("off")
axes[1].axis("off")
plt.show()
Мы применили к изображению фильтр Cобеля 📚[wiki], а точнее, одно из его ядер, дающее отклик на перепад яркости по вертикали.
"Отклик" — это величина яркости, которую мы получили на результирующем изображении.
Можно запрограммировать свой фильтр, который будет искать произвольный объект. Например, найдем крест на на изображении:
# fmt: off
cross = np.array([[0, 0 ,0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 1, 1, 1],
[0, 0, 0, 1, 0]])
# fmt: on
plt.subplot(1, 2, 1)
plt.imshow(cross, cmap="gray")
plt.axis("off")
plt.show()
Для этого создадим фильтр размером с объект ($3 \times 3$). В точках, где должны быть пиксели, принадлежащие объекту, поместим положительные значения, а там, где должен быть фон, — отрицательные.
# fmt: off
kernel_cs = np.array([[-1, 1, -1],
[ 1, 1, 1],
[-1, 1, -1]])
# fmt: on
При попадании такого фильтра на объект отрицательные значения обнулятся при перемножении с пикселями фона, а положительные — просуммируются и дадут высокий отклик.
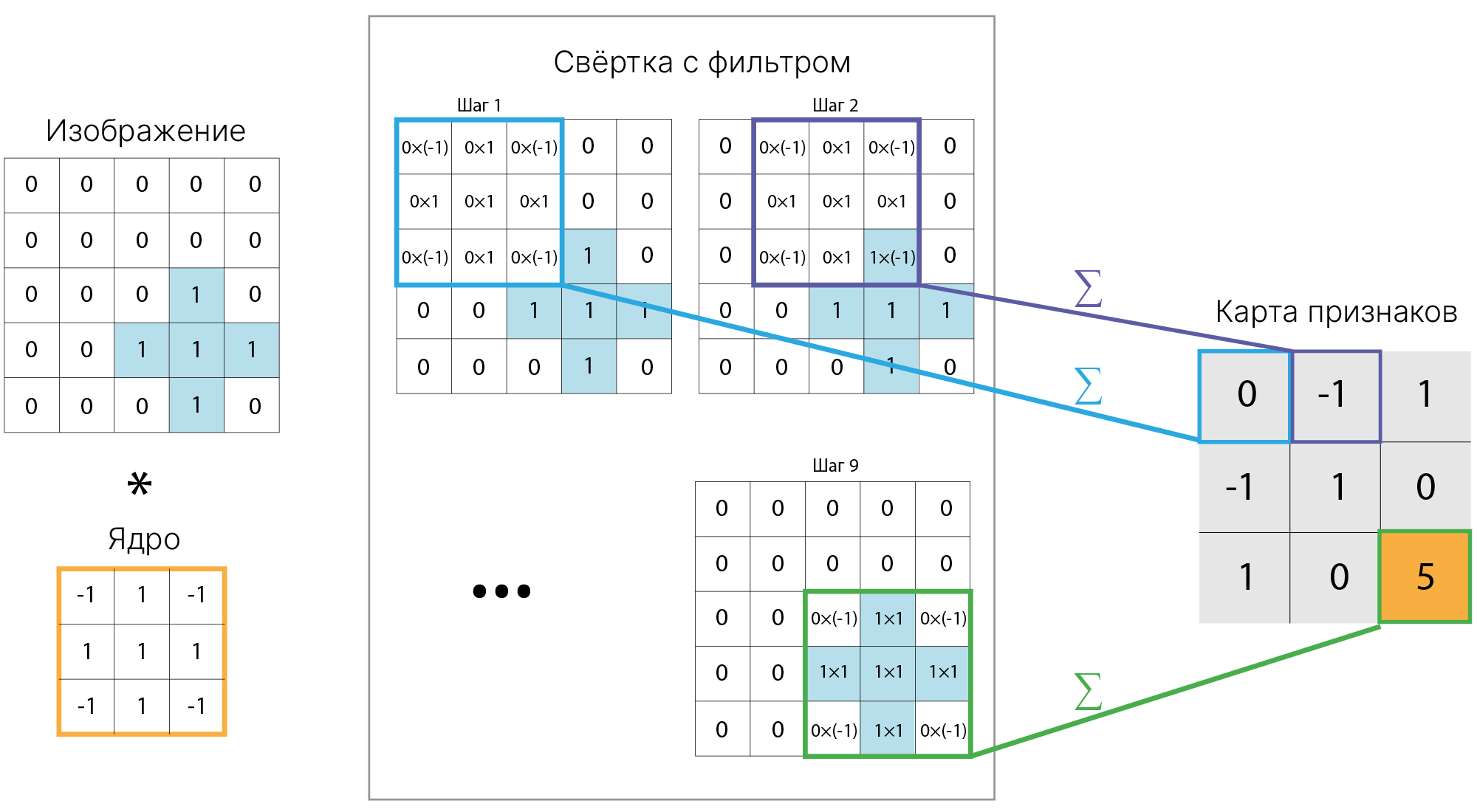
Проверим :
features = apply_filter(cross, kernel_cs)
plt.subplot(1, 2, 1)
plt.imshow(cross, cmap="gray")
plt.title("Image")
plt.subplot(1, 2, 2)
plt.xlim([0, 5])
plt.ylim([0, 5])
plt.imshow(features, extent=(1, 4, 1, 4))
plt.title("Features")
plt.colorbar(fraction=0.046, pad=0.04)
plt.show()
print("Features:\n", features)
Features: [[ 0. -1. 1.] [-1. 1. 0.] [ 1. 0. 5.]]
Такого рода фильтров люди придумали довольно много. Есть детектор углов Харриса 📚[wiki] или признаки Хаара 📚[wiki], которые успешно использовались для обнаружения лиц 📚[wiki] на фотографиях. Это примеры случаев, когда людям удалось подобрать удачные ядра фильтров для решения конкретных задач.
Мы хотим, чтобы модель могла обучаться решать различные задачи. И вместо того, чтобы вручную создавать фильтры, мы будем подбирать их значения в процессе обучения.
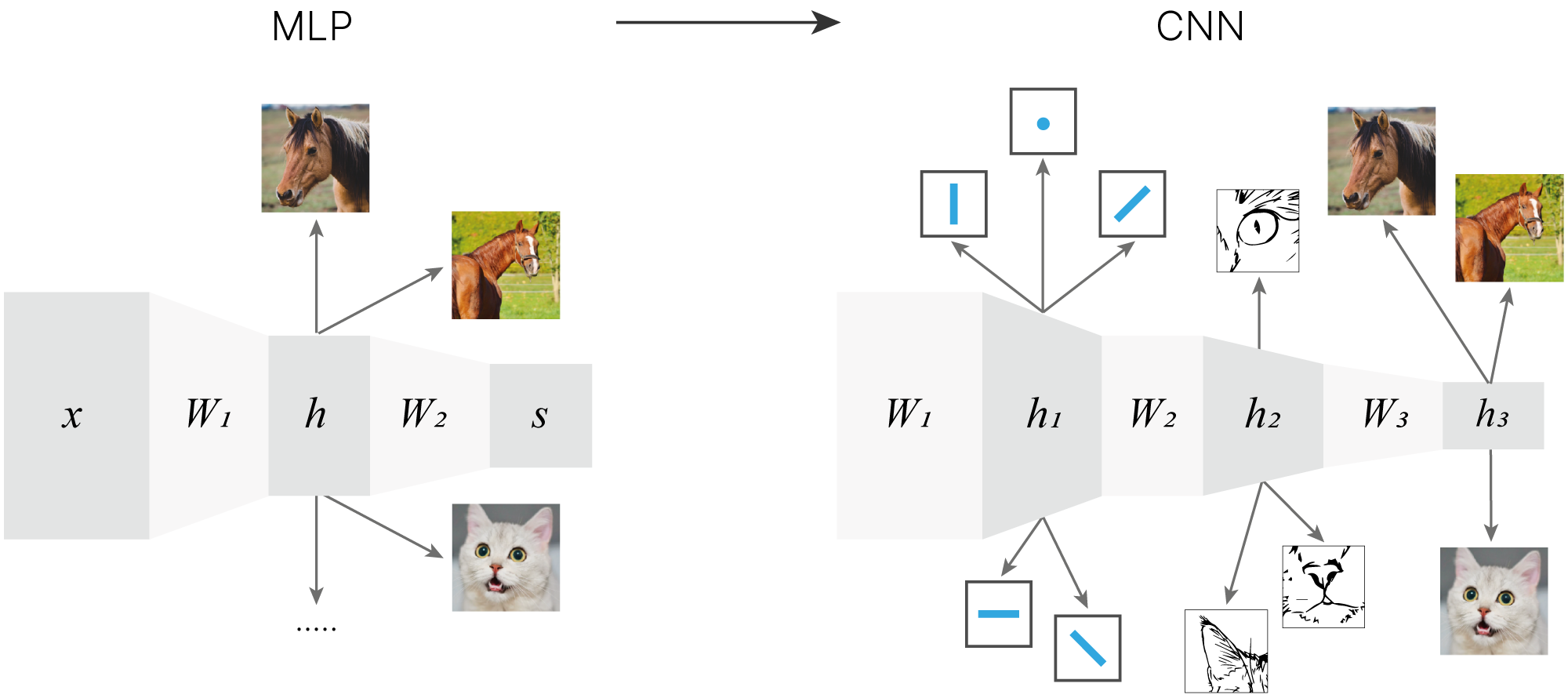
Тогда модель сможет выучивать шаблоны для небольших фрагментов изображения и станет инвариантной к сдвигу.
Операцию применения фильтра к изображению будем называть сверткой. Это определение не вполне соответствует математическому 📚[wiki], но повсеместно используется в DL.
По своей сути операция свёртки — это та же самая взвешенная сумма с добавлением свободного члена, используемая в полносвязных линейных слоях.
В фильтрах Собеля и Гаусса свободный член осутствовал, но в дальнейшем мы будем его использовать.
Давайте выполним свертку при помощи помощи линейного слоя: заменим код внутри цикла линейным слоем и убедимся, что результат вычислений не поменялся.
local_linear = nn.Linear(9, 1, bias=False) # 9 = 3 * 3 (weights shape: (3,3))
local_linear.weight.data[0] = torch.tensor(kernel_cs).flatten() # Bad practice
cross_in_tensor = torch.tensor(cross).float()
result = torch.zeros((3, 3))
for i in range(0, result.shape[0]):
for j in range(0, result.shape[1]):
segment = cross_in_tensor[i : i + 3, j : j + 3].flatten()
result[i, j] = local_linear(segment)
plt.subplot(1, 2, 1)
plt.imshow(cross, cmap="gray")
plt.title("Image")
plt.subplot(1, 2, 2)
plt.xlim([0, 5])
plt.ylim([0, 5])
plt.imshow(result.detach(), extent=(1, 4, 1, 4))
plt.title("Result")
plt.colorbar(fraction=0.046, pad=0.04)
plt.show()
print("Result:\n", result.detach())
Result:
tensor([[ 0., -1., 1.],
[-1., 1., 0.],
[ 1., 0., 5.]])
Ключевое отличие между линейным слоем и свёрткой заключается в том, что каждый нейрон линейного слойя получает на вход всё изображение сразу, а свёртка — небольшие фрагменты.
Так как при свертке для каждого фрагмента получаем свой отклик (признак), то для всего изображения получим уже массив признаков (feature map).
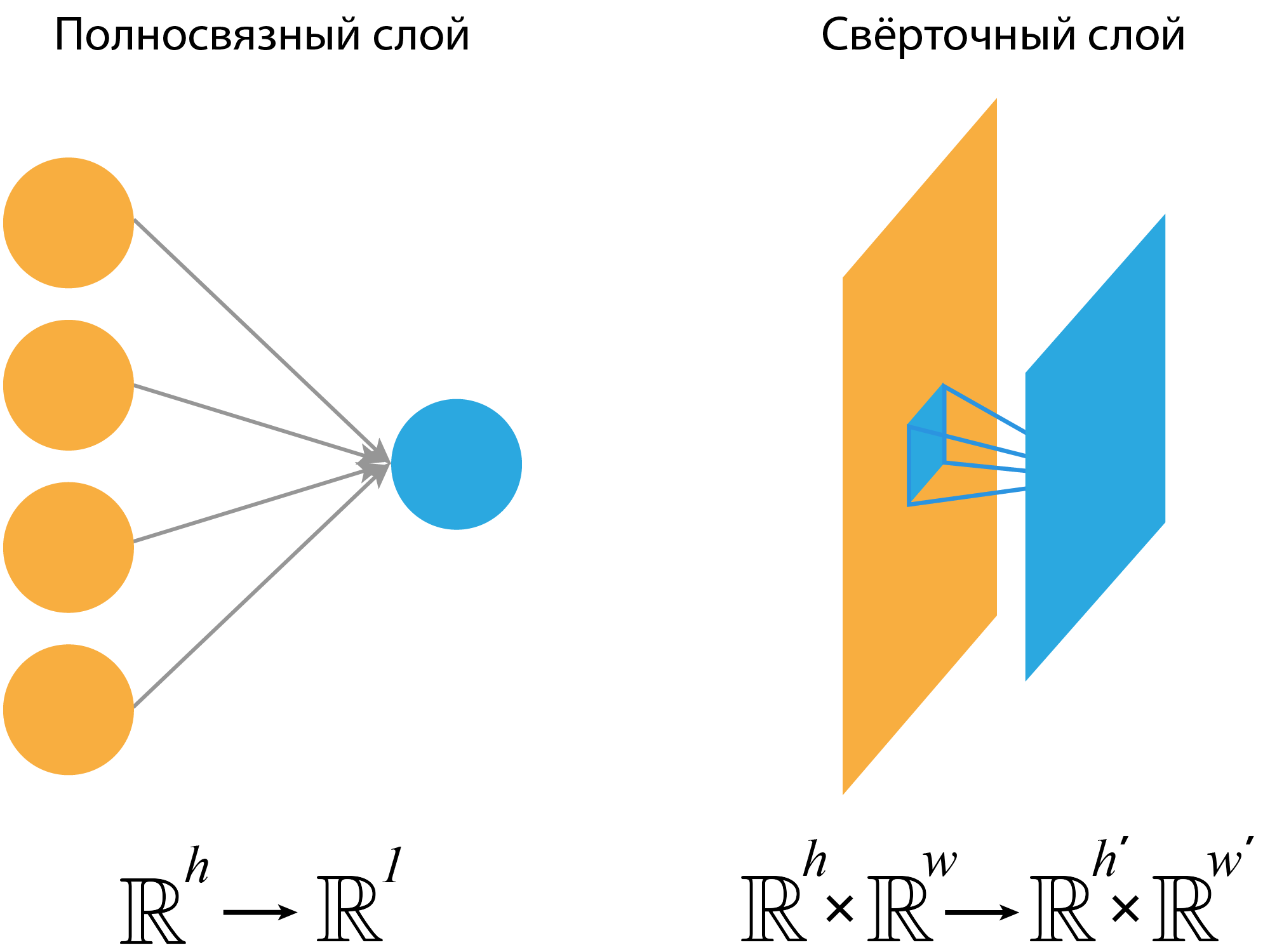
В PyTorch есть класс nn.Conv2d 🛠️[doc], который реализует операцию свертки для целого изображения.
import torch
import numpy as np
# fmt: off
cross = np.array([[0, 0 ,0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 1, 1, 1],
[0, 0, 0, 1, 0]])
kernel_cs = np.array([[-1, 1, -1],
[ 1, 1, 1],
[-1, 1, -1]])
# fmt: on
cross_in_tensor = torch.tensor(cross).float()
from torch.nn import Conv2d
conv = Conv2d(
in_channels=1, # what's this ?
out_channels=1, # what's this ?
kernel_size=(3, 3), # kernel.shape == 3x3
bias=False,
)
# conv2d accepts input of shape BxCxHxW
feature_map = conv(
cross_in_tensor.unsqueeze(0).unsqueeze(0)
) # add batch and channel dim
print(feature_map)
tensor([[[[ 0.0000, -0.2520, -0.3146],
[-0.2520, -0.4728, -0.2722],
[ 0.0938, 0.1015, 0.1447]]]], grad_fn=<ConvolutionBackward0>)
Так как изначально ядро нашего единственного фильтра (нейрона) инициализированно случайными небольшими значениями, то на выходе получается набор ничего не значащих чисел. Убедимся, что слой работает так, как мы ожидали, подменив ядро:
# data[0] because filter can have multiple kernels. see next chapter
conv.weight.data[0] = torch.tensor(kernel_cs) # replace original kernel
feature_map = conv(
cross_in_tensor.unsqueeze(0).unsqueeze(0)
) # add batch and channel dim
print("Feature map for cross\n", feature_map)
Feature map for cross
tensor([[[[ 0., -1., 1.],
[-1., 1., 0.],
[ 1., 0., 5.]]]], grad_fn=<ConvolutionBackward0>)
При создании экземпляра объекта класса nn.Conv2D 🛠️[doc] помимо размера ядра (kernel_size) мы передали в конструктор еще два параметра:
in_channels = 1 и out_channels = 1
Разберемся, что они означают.
in_channel — это количество каналов входного тензора (изображения).
В примерах выше мы рассматривали черно-белые 📚[wiki] изображения. Их также называют одноканальными изображениями, т. к. в них цвет пикселя определяется одним числом, характеризующим яркость.
Хранятся они в двумерном массиве размером $[H,W]$. Цветные изображения хранятся в трехмерных массивах $[H,W,C]$ или $[C,W,H]$, где $C$ — количество цветовых каналов. Для $\text{RGB}$-изображений $C=3$. Так как Conv2d рассчитан на работу с многоканальным входом, то в коде выше нам пришлось написать дополнительный unsqueeze(0), чтобы добавить к тензору с изображением это $3$-е измерение.
Важно, что для каждого канала будет создано дополнительное ядро фильтра.
conv_ch1 = Conv2d(in_channels=1, out_channels=1, kernel_size=5)
print("One channel kernel \t", conv_ch1.weight.shape)
conv_ch3 = Conv2d(in_channels=3, out_channels=1, kernel_size=5)
print("Three channel kernel \t", conv_ch3.weight.shape)
One channel kernel torch.Size([1, 1, 5, 5]) Three channel kernel torch.Size([1, 3, 5, 5])
Опробуем трехканальную свертку на цветном изображении:
!wget -q https://edunet.kea.su/repo/EduNet-web_dependencies/dev-2.0/L06/cat.jpg
from PIL import Image
cat_in_pil = Image.open("cat.jpg")
display(cat_in_pil)
Изображение из формата Pillow надо превратить в torch.Tensor:
cat_in_np = np.array(cat_in_pil) # pillow -> numpy
cat_in_float = cat_in_np.astype(np.float32) / 255 # int->float
cat_in_tensor = torch.tensor(cat_in_float) # np -> torch
try:
conv_ch3(cat_in_tensor.unsqueeze(0)) # add batch dimension
except Exception as e:
print("Error: \n", e)
Error: Given groups=1, weight of size [1, 3, 5, 5], expected input[1, 192, 192, 3] to have 3 channels, but got 192 channels instead
Получили ошибку, связанную с количеством каналов. Дело в том, что в PyTorch, в отличие от OpenCV, TensorFlow и ряда других библиотек, каналы (RGB) идут в первом, а не в последнем измерении тензора, описывающего картинку.
OpenCV, TensorFlow, Pillow, etc. : $[\text{Batch}, \text{Height}, \text{Width}, \text{Channels}]$
PyTorch : $[\text{Batch}, \text{Channels}, \text{Height}, \text{Width}]$
Придется сделать дополнительное преобразование, чтобы каналы оказались на том месте, где их ожидает PyTorch:
print("Original \t", cat_in_tensor.shape, "HWC")
cat_in_tensor_channel_first = cat_in_tensor.permute(2, 0, 1) # HWC -> CHW
print("Torch style \t", cat_in_tensor_channel_first.shape, "CHW")
Original torch.Size([192, 192, 3]) HWC Torch style torch.Size([3, 192, 192]) CHW
Теперь можно подать изображение на вход модели, предварительно добавив batch-размерность:
one_image_batch = cat_in_tensor_channel_first.unsqueeze(0)
out = conv_ch3(one_image_batch)
print("No error!")
No error!
Нет необходимости проделывать все эти манипуляции вручную, так как в torchvision реализованы класс ToTensor 🛠️[doc] и функция to_tensor 🛠️[doc], которые выполняют эти преобразования.
Убедимся, что тензор, преобразованный нами вручную, и тензор, получившийся после применения функции to_tensor, совпали:
from torchvision.transforms.functional import to_tensor
cat_in_tensor2 = to_tensor(cat_in_pil)
print(cat_in_tensor2.shape)
print(
"Tensor almost equal: ",
torch.allclose(cat_in_tensor_channel_first, cat_in_tensor2), # float comparsion
)
torch.Size([3, 192, 192]) Tensor almost equal: True
Теперь посмотрим на форму выхода, полученного нами ячейкой выше:
print("Output feature map size:", out.shape) # first dim is batch
Output feature map size: torch.Size([1, 1, 188, 188])
Такую размерность имеет выход единственного нейрона в нашем сверточном слое.
На входе несколько каналов (3), на выходе остался один канал. Как же комбинируются результаты сверток в разных каналах?
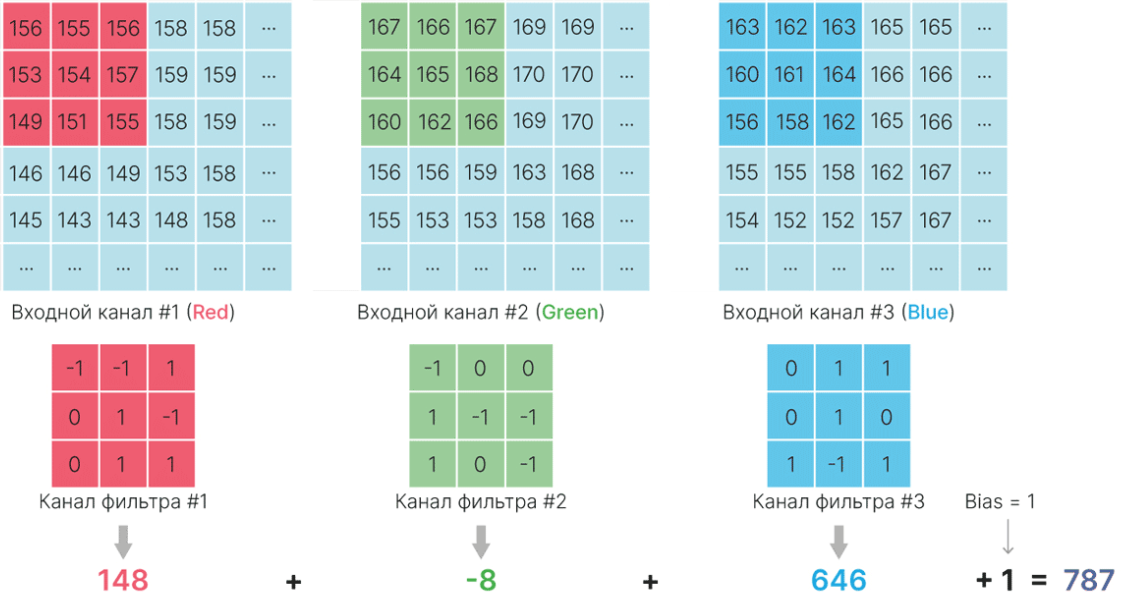
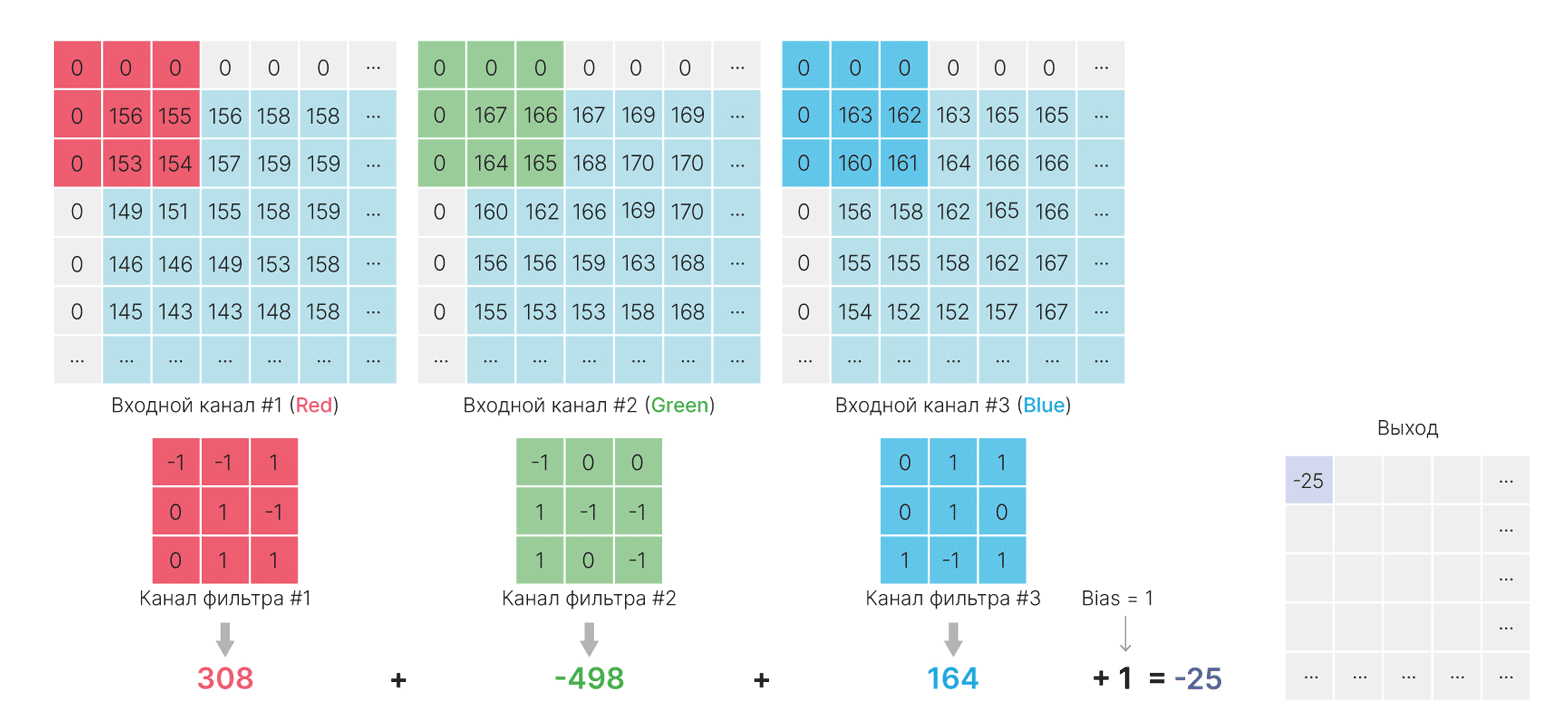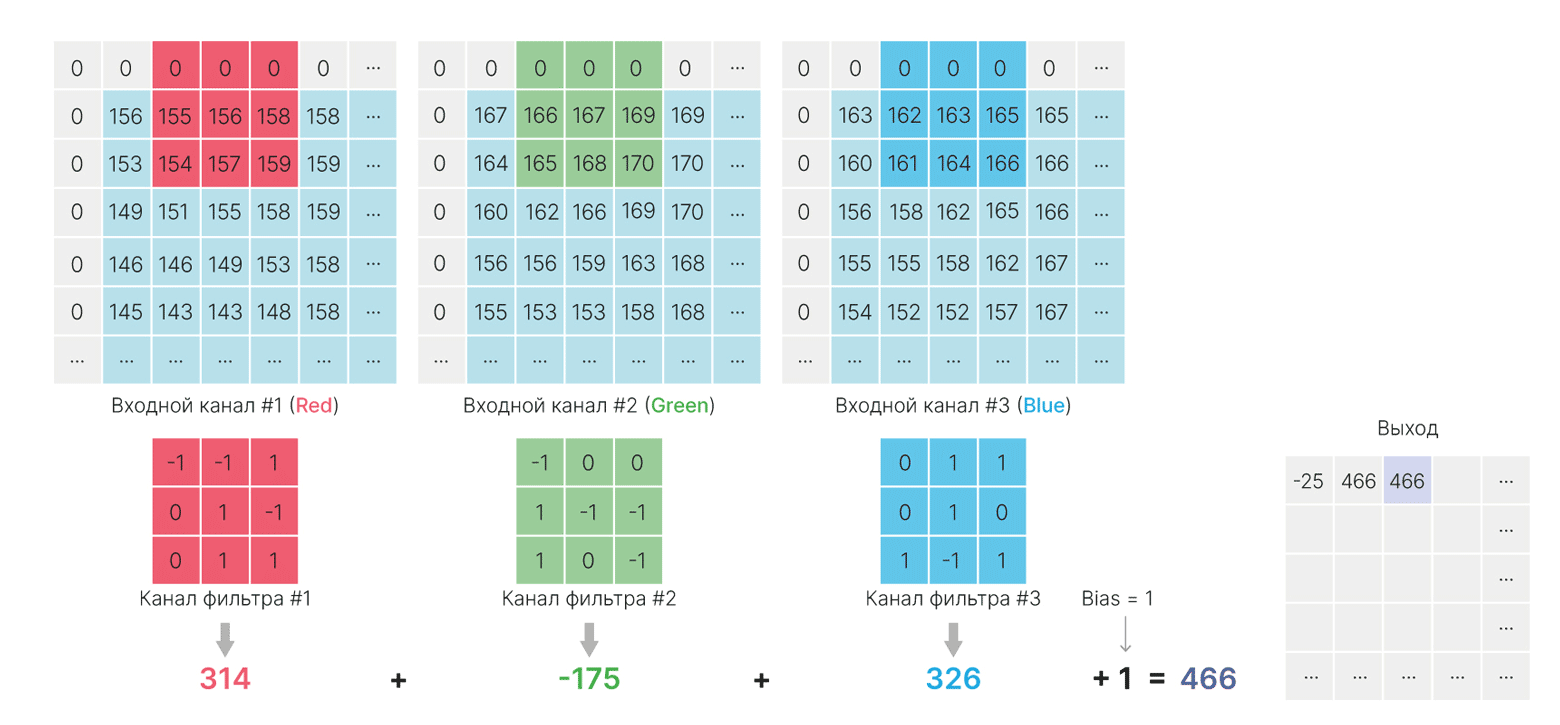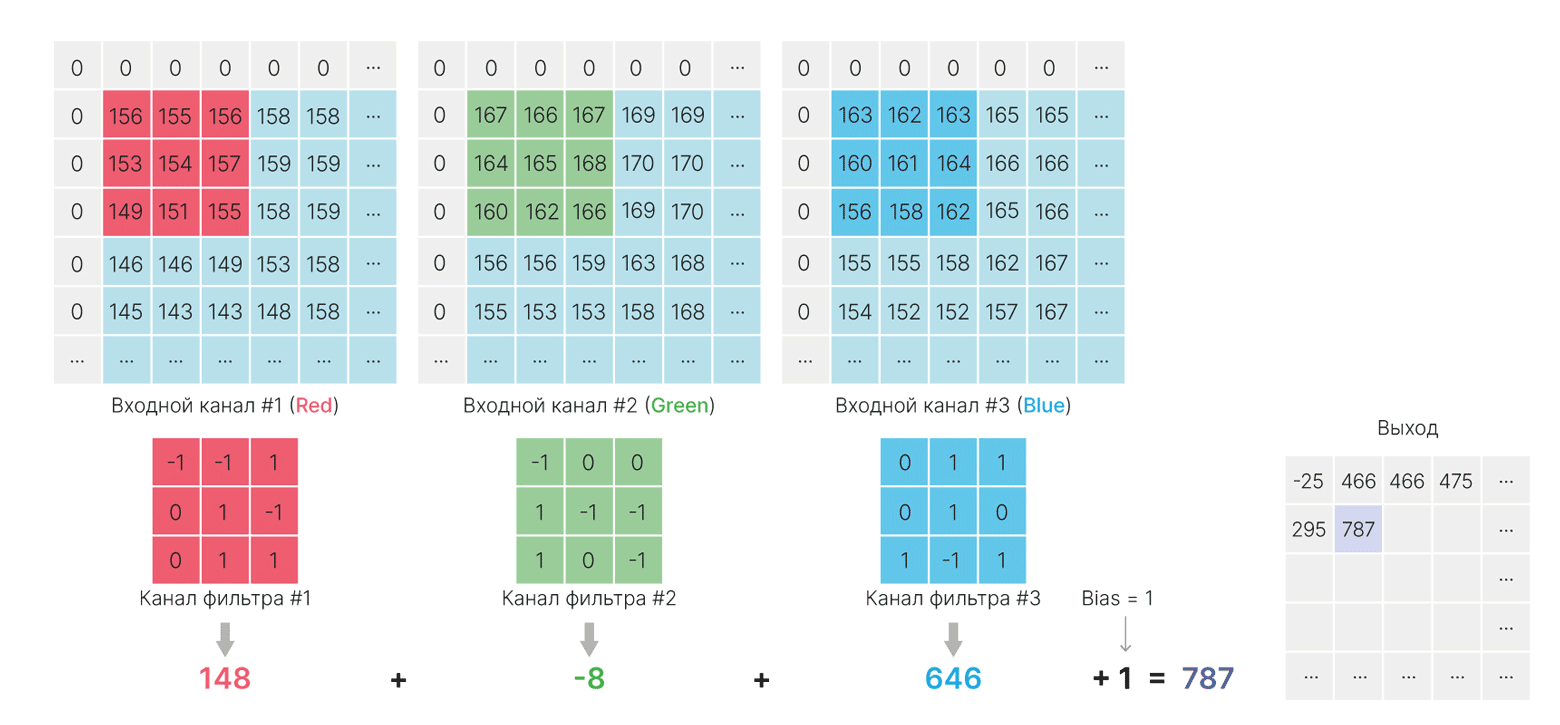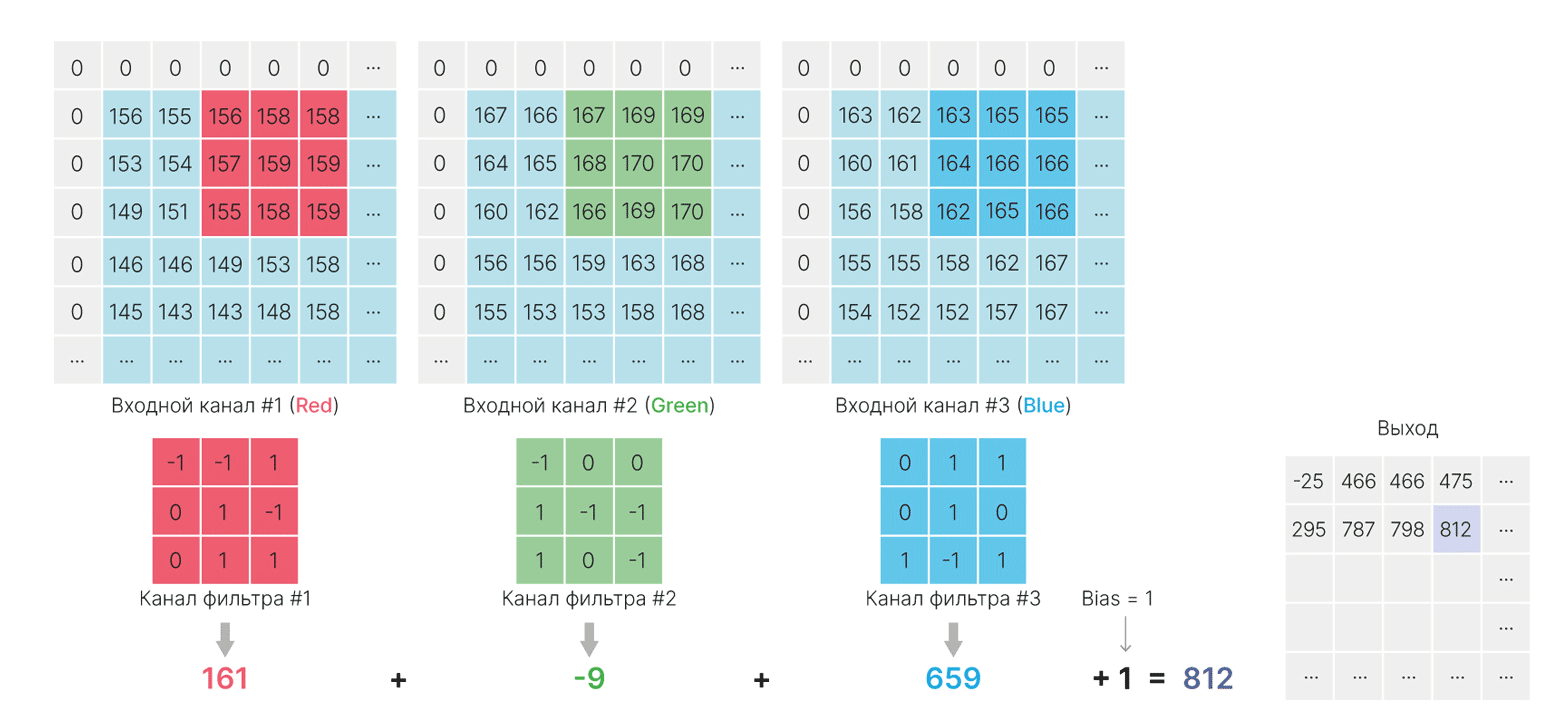
Результаты сверток всех ядер фильтра с соответствующими входными каналами просто суммируются:
$\large \displaystyle \text{feature_map}(x,y) = \sum_{c}^{C} \sum_{i}^{H} \sum_{j}^{W}k_c[i,j]I_c[x+j,y+i] +bias,$
$C$ — количество каналов,
$H, W$ — высота и ширина ядра фильтра,
$K_c$ — ядро для канала $c$,
$I$ — изображение (массив $С\times H\times W$),
$I_c$ — канал изображения номер $c$ (срез массива $I$, соответствующий каналу изображения номер $c$).
В силу коммутативности суммы не важно, в каком порядке будут складываться элементы. Можно считать, что каждый элемент входа сначала умножается на свой коэффициент из ядра, а уже затем все суммируется.
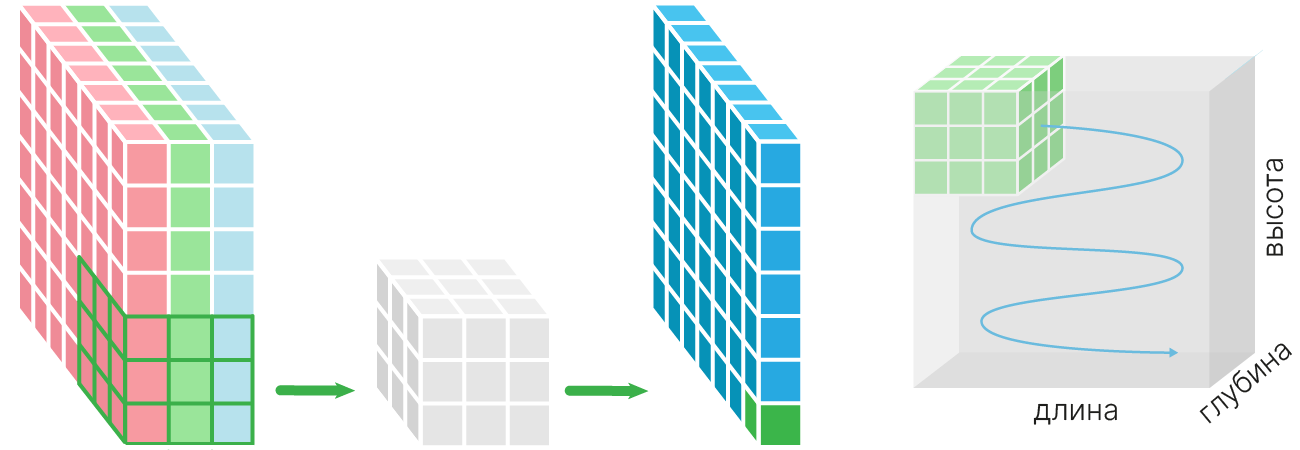
Так выглядит выход одного нейрона, который задается несколькими ядрами и смещением (bias).
При этом bias один на весь фильтр.
print("Kernels", conv_ch3.weight.shape)
print("Biases", conv_ch3.bias.shape)
Kernels torch.Size([1, 3, 5, 5]) Biases torch.Size([1])
Входные данные не всегда будут трехканальными цветными RGB 📚[wiki]-изображениями, в которых цвет пикселя определяется тремя числами, характеризующими три основных цвета (красный, зеленый и синий).
Входной тензор может иметь произвольное количество каналов. Например: марсоход Opportunity для получения изображений использовал 13 каналов ✏️[blog].
Более того, в качестве входного тензора можно использовать не изображение, а карту активаций предыдущего сверточного слоя.
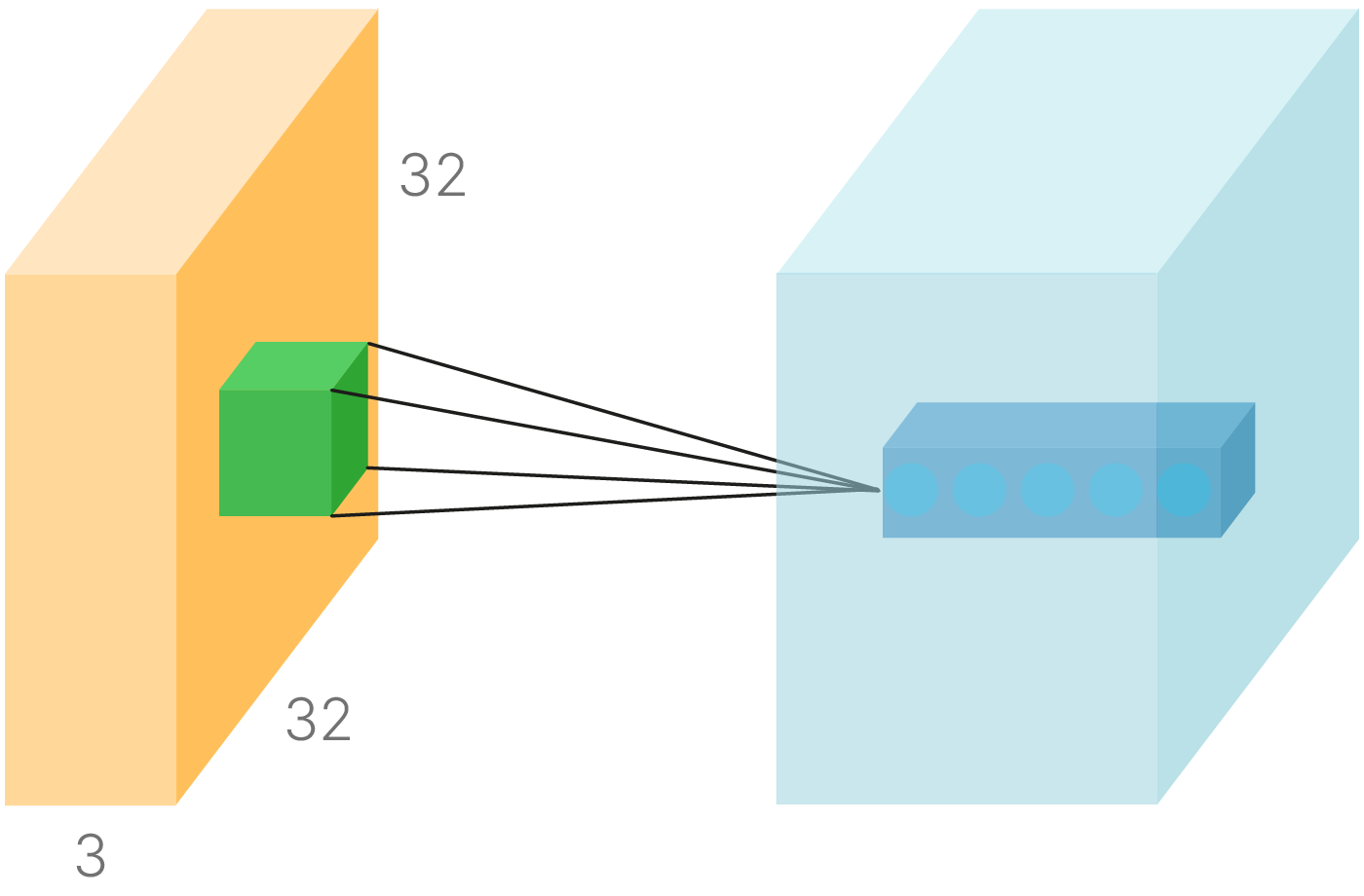
Возвращаемся ко второму параметру конструктора nn.Conv2D —
out_channels = 1. Этот параметр задает количество фильтров слоя.
conv35 = Conv2d(in_channels=3, out_channels=5, kernel_size=3)
out = conv35(cat_in_tensor_channel_first)
print(f"weights shape: {conv35.weight.shape}") # 5 filters 3x3x3
print(f"weights shape: {conv35.bias.shape}") # one bias per filter
weights shape: torch.Size([5, 3, 3, 3]) weights shape: torch.Size([5])
В линейном слое каждый нейрон учился активироваться на некий шаблон, например, красную машину или смотрящую направо лошадь.
Мы хотим, чтобы нейроны сверточного слоя также активировались на различные паттерны (например, ухо, нос, глаз и т.д.). Для каждого паттерна нам нужен свой нейрон $⇒$ свой фильтр.
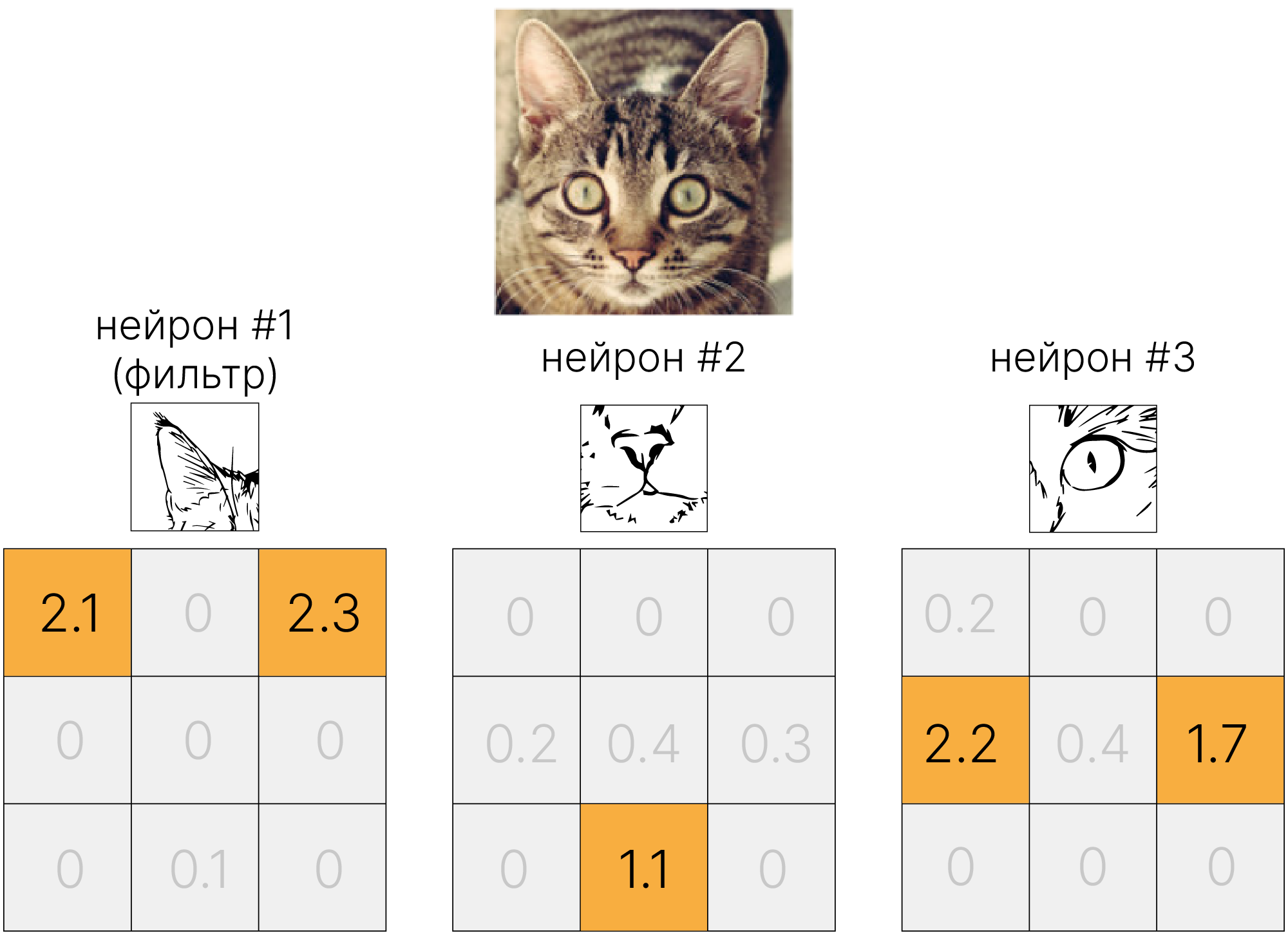
Каждый нейрон сформирует свою карту признаков, размером $1\times H_{out}\times W_{out}$. А на выходе слоя будет их конкатенация:
print(f"result shape: {out.shape}") # 5 feature map
result shape: torch.Size([5, 190, 190])
При объединении этих карт получится тензор размерности $C_{out}\times H_{out} \times W_{out}$, где $C_{out}$ — количество фильтров.
На изображении ниже продемонстрирован результат применения сверточного слоя, содержащего $5$ фильтров, к изображению из CIFAR-10.
Стоит отметить, что, в отличие от полносвязного слоя, свёрточный слой не требует информации о количестве значений во входном представлении и может быть использован как для представлений $C_{in} \times 32 \times 32$, так и для $C_{in} \times 100 \times 100$. Словом, представления могут иметь практически любой размер, главное, чтобы пространственные размеры не были меньше размеров ядра свёртки.
Карта признаков после применения функции активации может быть передана на вход следующей операции свёртки.
from torch.nn.functional import relu
conv_1 = torch.nn.Conv2d(
in_channels=3, # Number of input channels (3 for RGB images)
out_channels=6, # Number of filters/output channels
kernel_size=5,
)
conv_2 = torch.nn.Conv2d(
in_channels=6, # Number of input channels (3 for RGB images)
out_channels=10, # Number of filters/output channels
kernel_size=5,
)
img = torch.randn((1, 3, 32, 32)) # 1-batch size, 3-num of channels, (32,32)-img size
print(f"img shape: {img.shape}")
out_1 = conv_1(img)
print(f"out_1 shape: {out_1.shape}") # [1, 6, 28, 28]
out_2 = conv_2(relu(out_1))
print(f"out_2 shape: {out_2.shape}") # [1, 10, 24, 24]
img shape: torch.Size([1, 3, 32, 32]) out_1 shape: torch.Size([1, 6, 28, 28]) out_2 shape: torch.Size([1, 10, 24, 24])
Заметим, что после свёртки ширина $W_{out}$ и высота $H_{out}$ карты признаков будут отличаться от пространственных размерностей $W_{in}$ и $H_{in}$ исходного тензора. К примеру, при обработке трёхканального тензора размера $32\times32$ ядром размера $5\times5$ можно будет произвести лишь $27$ сдвигов $(32 - 5)$ по вертикали и столько же по горизонтали. Но при этом размер итоговой карты признаков будет равен $28 \times 28$, поскольку первый ряд (либо столбец) можно получить без сдвигов по вертикали либо горизонтали соответственно. При повторном применении фильтра размер каждой из сторон уменьшится ещё на $4$.
Итоговое значение $N'$ пространственной размерности $N$ для квадратного фильтра $K \times K$ фильтра $F$ вычисляется по следующей формуле: $$\large N' = N - K + 1$$.
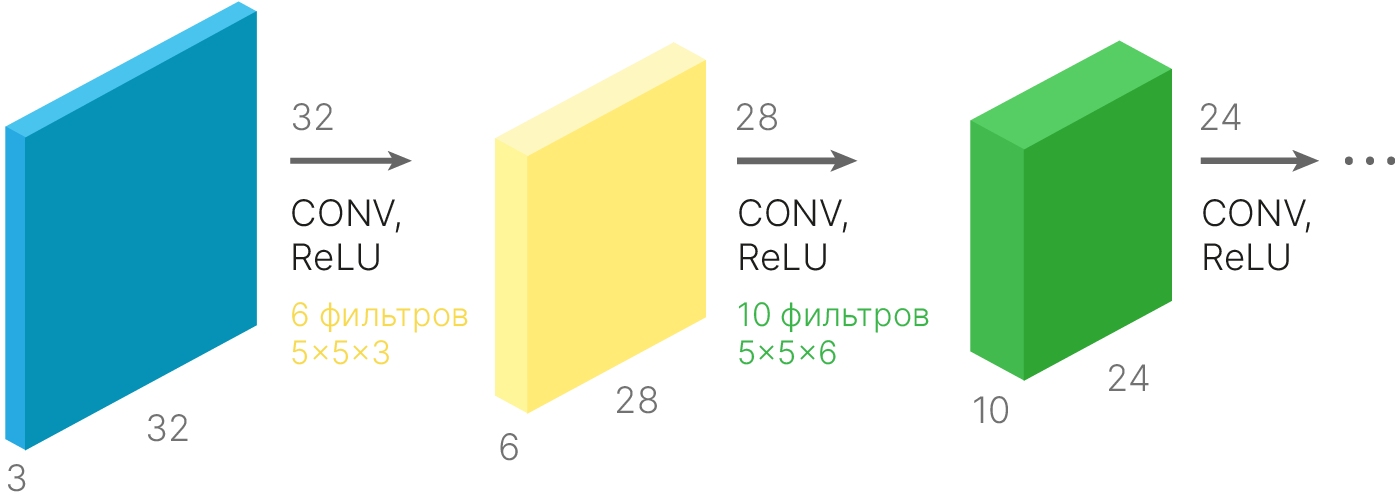
Заметим, что при уменьшении размера представлений пиксели, находящиеся около краёв, участвуют в значительно меньшем количестве свёрток, чем пиксели в середине, хотя информация в них не обязательно менее ценна, чем информация из центральных пикселей. К примеру, пиксель в верхнем левом углу представления вне зависимости от размера фильтра будет принимать участие лишь в одной свёртке, и информация о нём будет сохранена лишь в верхнем левом углу нового представления.
Для борьбы с описанной выше проблемой применяется набивка/дополнение входного тензора (англ. padding). В ходе него ширина и высота тензора увеличиваются за счёт приписывания столбцов и строк с некоторыми значениями. К примеру, на изображении ниже перед свёрткой ядром размера $3\times3$ был применён padding нулями.
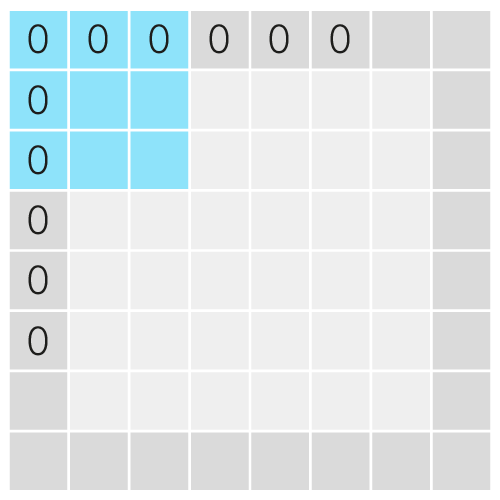
На примере убедимся, что это позволит нам сохранить пространственные размерности тензоров.
img = torch.randn((1, 1, 5, 5)) # create random image BCHW
print(f"Original tensor:\nshape:{img.shape}")
conv_3 = torch.nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3)
conved_3 = conv_3(img)
print("Shape after convolution layer(kernel 3x3):", conved_3.shape)
Original tensor: shape:torch.Size([1, 1, 5, 5]) Shape after convolution layer(kernel 3x3): torch.Size([1, 1, 3, 3])
Карта признаков меньше, чем вход. Теперь добавим padding:
# add zeros to image manually
padded_img = torch.zeros((1, 1, 7, 7)) # create zeros array to insert image in center
padded_img[:, :, 1:-1, 1:-1] += img # insert image, we get image arounded by zeros
print(f"\nPadded tensor:\nshape:{padded_img.shape}:\n {padded_img}")
conved_pad_3 = conv_3(padded_img)
print("\n\nPadded shape:", padded_img.shape)
print("Shape after convolution with padding(kernel 3x3):", conved_pad_3.shape)
Padded tensor:
shape:torch.Size([1, 1, 7, 7]):
tensor([[[[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, -0.7762, -0.8809, 2.9101, 1.1978, -1.0568, 0.0000],
[ 0.0000, -0.4706, 0.0981, 0.8564, 1.5882, -0.2351, 0.0000],
[ 0.0000, 0.2247, 0.8475, 0.0281, 1.2842, 0.2463, 0.0000],
[ 0.0000, 0.5440, -0.5140, 0.0858, 0.3820, 0.1245, 0.0000],
[ 0.0000, 0.1286, 0.0221, -1.2747, -0.1029, 0.4962, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]]])
Padded shape: torch.Size([1, 1, 7, 7])
Shape after convolution with padding(kernel 3x3): torch.Size([1, 1, 5, 5])
Размер выхода равен размеру входа.
Однако если мы увеличим размер ядра до $5\times5$, то увидим, что, несмотря на padding, выход снова стал меньше входа:
conv_5 = torch.nn.Conv2d(in_channels=1, out_channels=1, kernel_size=5)
conved_pad_5 = conv_5(padded_img)
print("Original shape:", img.shape)
print("Shape after convolution with padding(kernel 5x5):", conved_pad_5.shape)
Original shape: torch.Size([1, 1, 5, 5]) Shape after convolution with padding(kernel 5x5): torch.Size([1, 1, 3, 3])
Дополнение одним рядом и одним столбцом не является универсальным решением: для фильтра размером $5$ размер выходного тензора всё равно отличается от входного. Если мы немного видоизменим полученную выше формулу (используя размер дополнения $P$), то получим: $$\large N' = N + 2\cdot P - K + 1$$
Для того, чтобы пространственные размеры не изменялись ($N' = N$), для разных размеров фильтра требуются разные размеры дополнения. В общем случае для размера фильтра $F$ требуемый размер дополнения: $$\large P = \frac{K-1}{2}$$
Теперь реализуем padding, используя инструменты библиотеки PyTorch, и сравним его с ручным добавлением padding:
# conv layer without padding (padding=0 by default)
conv_3 = torch.nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=0)
# conv layer with padding = 1 (add zeros)
conv_3_padded = torch.nn.Conv2d(
in_channels=1, out_channels=1, kernel_size=3, padding=1
) # Padding added 1 zeros line to all four sides of the input
original = conv_3(padded_img)
padded = conv_3_padded(img)
print(f"Explicitly padded:\n{original.shape}")
print(f"\nImplicitly padded:\n{padded.shape}")
Explicitly padded: torch.Size([1, 1, 5, 5]) Implicitly padded: torch.Size([1, 1, 5, 5])
Кроме чисел параметр padding может принимать значение "same" — тогда padding будет рассчитан автоматически так, чтобы размер выходного тензора не отличался от размера входного тензора, или "valid" — отсутствие дополнения.
Теперь мы можем заменить часть линейных слоев нашей модели на сверточные. Но если решается задача классификации, то последний слой по-прежнему должен быть линейным.
Поскольку операция свертки является линейной (мы убедились в этом, когда выполняли ее при помощи линейного слоя), то функция активации (например, ReLU) по-прежнему требуется.
Так как функция активации применяется к тензору поэлементно, не важно, какую именно форму имеет тензор, а значит и какой слой находился передней ней: полносвязный или сверточный.
Простейшая модель для MNIST может выглядеть примерно так:
import torch
from torch import nn
batch_size = 1
input = torch.randn((batch_size, 1, 28, 28))
model = torch.nn.Sequential(
nn.Conv2d(
in_channels=1, out_channels=3, kernel_size=5
), # after conv shape: [batch_size,3,24,24]
nn.ReLU(), # Activation doesn't depend on input shape
nn.Conv2d(
in_channels=3, out_channels=6, kernel_size=3
), # after conv shape: [batch_size,6,22,22]
nn.ReLU(),
nn.Flatten(), # 6*22*22=2904
nn.Linear(2904, 100),
nn.ReLU(), # Activation doesn't depend on input shape
nn.Linear(100, 10), # 10 classes, like a cifar10
)
out = model(input)
print(f"out shape: {out.shape}")
out shape: torch.Size([1, 10])
Поскольку полносвязный слой принимает на вход набор векторов, а сверточный — возвращает набор трёхмерных тензоров, нам нужно превратить эти тензоры в вектора. Для этого используется объект класса nn.Flatten 🛠️[doc].
Он преобразовывает данные на входе в вектор, сохраняя при этом первое (batch) измерение.
Ниже примеры других функций, которыми можно выполнить аналогичное преобразование:
input = torch.randn((16, 3, 32, 32))
batch_size = input.shape[0]
print("class Flatten\t", nn.Flatten()(input).shape)
print(
"view \t\t", input.view(batch_size, -1).shape
) # data stay in same place in memory
print("reshape \t", input.reshape(batch_size, -1).shape) # data may be moved
print("method flatten \t", input.flatten(1).shape)
class Flatten torch.Size([16, 3072]) view torch.Size([16, 3072]) reshape torch.Size([16, 3072]) method flatten torch.Size([16, 3072])
Нейросетевая модель из предыдущего примера позволяет в общем случае понять структуру свёрточных нейронных сетей: после некоторого количества свёрточных слоёв, извлекающих локальную пространственную информацию, идут полносвязные слои (как минимум в количестве одного), сопоставляющие извлечённую информацию.
Внутри свёрточных слоёв происходит следующий процесс: первые слои нейронных сетей имеют малые рецептивные поля, т. е. им соответствует малая площадь на исходном изображении. Такие нейроны могут активироваться лишь на некоторые простые шаблоны (по типу углов или освещённости).
Нейроны следующего слоя уже имеют большие рецептивные поля, в результате чего в картах активации появляется информация о более сложных паттернах. С каждым слоем свёрточной нейронной сети рецептивное поле нейронов увеличивается, увеличивается и сложность шаблонов, на которые может реагировать нейрон. В последних слоях рецептивное поле нейрона должно быть размером со всё исходное изображение. Пример можно увидеть на схеме ниже.
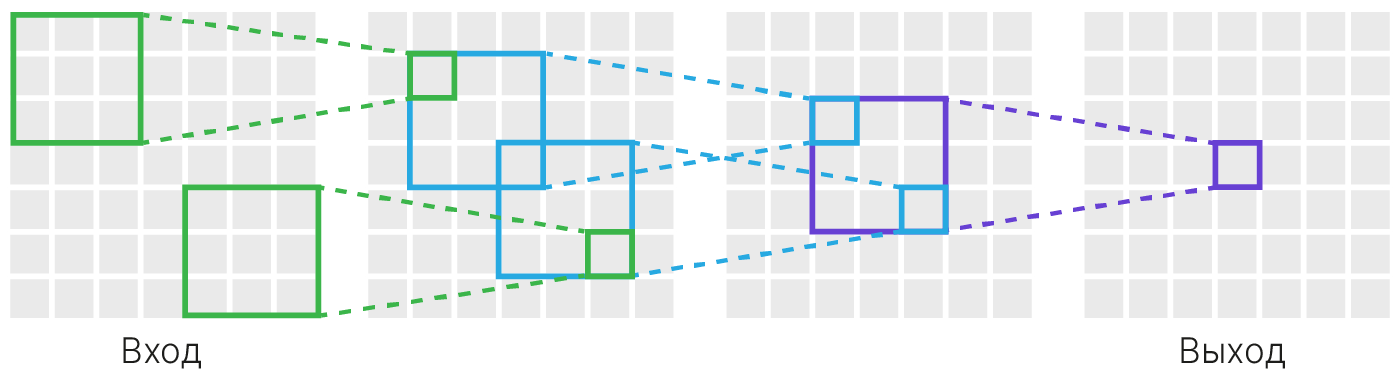
Если на первом слое рецептивное поле имело размер $K \times K$, то после свёртки фильтром $K\times K$ оно стало иметь размер $(2K-1) \times (2K-1)$, то есть увеличилось на $K-1$ по каждому из направлений. Несложно самостоятельно убедиться, что данная закономерность сохранится при дальнейшем применении фильтров того или иного размера.
Однако при обработке больших изображений нам потребуется очень много слоев, чтобы нейрон "увидел" всю картинку.
К примеру, для изображения $1024\times1024$ понадобится сеть глубиной $\approx510$ сверточных слоев.
Такая модель потребует огромного количества памяти и вычислительных ресурсов. Чтобы избежать этого, будем сами уменьшать размеры карт признаков, при этом рецептивные поля нейронов будут расти.
До этого мы двигали фильтр на один пиксель, то есть перемещались с шагом (stride) один.
Если двигать фильтр с большим шагом, то размер выходной карты признаков (feature map) будет уменьшаться кратно шагу, и рецептивные поля нейронов будут расти быстрее.
Для изменения шага свертки в конструкторе nn.Conv2d 🛠️[doc] есть параметр stride.
dummy_input = torch.randn(1, 1, 5, 5)
conv_s1 = nn.Conv2d(in_channels=1, out_channels=3, kernel_size=3, stride=(1, 1))
conv_s2 = nn.Conv2d(1, 3, 3, stride=2) # bypass par. names, stride = (2, 2)
out_stride1 = conv_s1(dummy_input)
out_stride2 = conv_s2(dummy_input)
print("Out with stride 1", out_stride1.shape)
print("Out with stride 2", out_stride2.shape)
Out with stride 1 torch.Size([1, 3, 3, 3]) Out with stride 2 torch.Size([1, 3, 2, 2])

При этом важно заметить, что в некоторых случаях часть данных может не попасть в свёртку. К примеру, при $N = 7,\, K = 3,\, S = 3$. В данном случае: $$\large N' = 1 + \frac{7 - 3}{3} = 2\frac13.$$ В подобных ситуациях часть изображения не захватывается, в чём мы можем убедиться на наглядном примере:
# Create torch tensor 7x7
# fmt: off
input = torch.tensor([[[[1, 1, 1, 1, 1, 1, 99],
[1, 1, 1, 1, 1, 1, 99],
[1, 1, 1, 1, 1, 1, 99],
[1, 1, 1, 1, 1, 1, 99],
[1, 1, 1, 1, 1, 1, 99],
[1, 1, 1, 1, 1, 1, 99],
[1, 1, 1, 1, 1, 1, 99]]]], dtype=torch.float)
# fmt: on
print(f"input shape: {input.shape}")
conv = torch.nn.Conv2d(
in_channels=1, # Number of channels
out_channels=1, # Number of filters
kernel_size=3,
stride=3,
bias=False, # Don't use bias
)
conv.weight = torch.nn.Parameter(
torch.ones((1, 1, 3, 3))
) # Replace random weights to ones
out = conv(input)
print(f"out shape: {out.shape}")
print(f"out:\n{out}")
input shape: torch.Size([1, 1, 7, 7])
out shape: torch.Size([1, 1, 2, 2])
out:
tensor([[[[9., 9.],
[9., 9.]]]], grad_fn=<ConvolutionBackward0>)
Видно, что столбец с числами $99$ просто не попал в свертку.
Поэтому на практике подбирают padding таким образом, чтобы при stride = 1 размер карты признаков на выходе был равен входу, а затем делают свертку со stride = 2.
Казалось бы, с увеличением шага $S$ рецептивное поле не выросло — как увеличивалось с $1$ до $K$, так и увеличивается. Однако обратим внимание на другое: если раньше размерность $N$ становилась $N - F + 1$, то теперь она станет $\displaystyle 1 + \frac{N-F}{S}$.
В результате если раньше следующий фильтр с размером $K'$ имел рецептивное поле:$$\displaystyle N \cdot \frac{K'}{N'} = N \cdot \frac{K'}{N - F + 1},$$
то теперь: $$\displaystyle N \cdot \frac{K'}{N'} = N \cdot \frac{K'}{1 + \frac{N-F}{S}}.$$
Понятно, что $$\displaystyle \frac{K'}{N - F + 1} \leq \frac{K'}{1 + \frac{N-F}{S}},$$ поэтому рецептивное поле каждого нейрона увеличивается.
Другим вариантом стремительного увеличения размера рецептивного поля является использование дополнительных слоёв, требующих меньшее количество вычислительных ресурсов. Слои субдискретизации прекрасно выполняют эту функцию: подобно свёртке, производится разбиение изображения на небольшие сегменты, внутри которых выполняются операции, не требующие использования обучаемых весов. Два популярных примера подобных операций: получение максимального значения (max pooling) и получение среднего значения (average pooling).
Аналогично разбиению на сегменты при свёртке, слои субдискретизации имеют два параметра: размер фильтра $K$ (то есть, каждого из сегментов) и шаг $S$ (stride). Аналогично свёрткам, при применении субдискретизации формула размера стороны будет $\displaystyle N' = 1+ \frac{N-K}{S}.$
Ниже приведён пример использования операций max pooling и average pooling при обработке массива.

Реализуем это в коде:
# create tensor 4x4
# fmt: off
input = torch.tensor([[[[1, 1, 2, 4],
[5, 6, 7, 8],
[3, 2, 1, 0],
[1, 2, 3, 4]]]], dtype=torch.float)
# fmt: on
max_pool = torch.nn.MaxPool2d(kernel_size=2, stride=2)
avg_pool = torch.nn.AvgPool2d(kernel_size=2, stride=2)
print("Input:\n", input)
print("Max pooling:\n", max_pool(input))
print("Average pooling:\n", avg_pool(input))
Input:
tensor([[[[1., 1., 2., 4.],
[5., 6., 7., 8.],
[3., 2., 1., 0.],
[1., 2., 3., 4.]]]])
Max pooling:
tensor([[[[6., 8.],
[3., 4.]]]])
Average pooling:
tensor([[[[3.2500, 5.2500],
[2.0000, 2.0000]]]])
Важно отметить, что субдискретизация выполняется по каждому из каналов отдельно, в результате чего количество каналов не меняется, в отличие от применения фильтра при свёртке. К примеру, ниже можно увидеть визуализацию применения max pooling к одному из каналов тензора, имеющего $64$ канала.
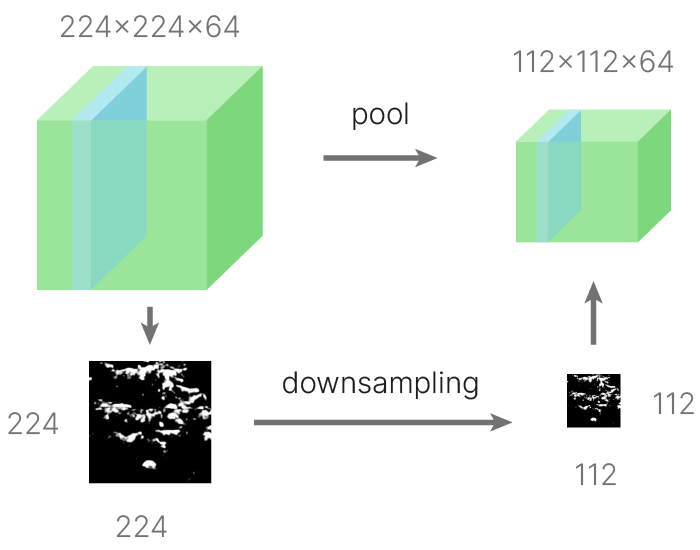
С помощью субдискретизации и свертки с шагом больше единицы мы можем регулировать пространственные размеры (ширину и высоту) карты признаков.
Количество каналов можно регулировать при помощи параметра out_channels. Если при этом количество каналов уменьшается, то таким образом мы обобщаем признаки.
Обычно если хотят уменьшить количество каналов в карте признаков, то используют свертку с размерами ядра $1\times1$.
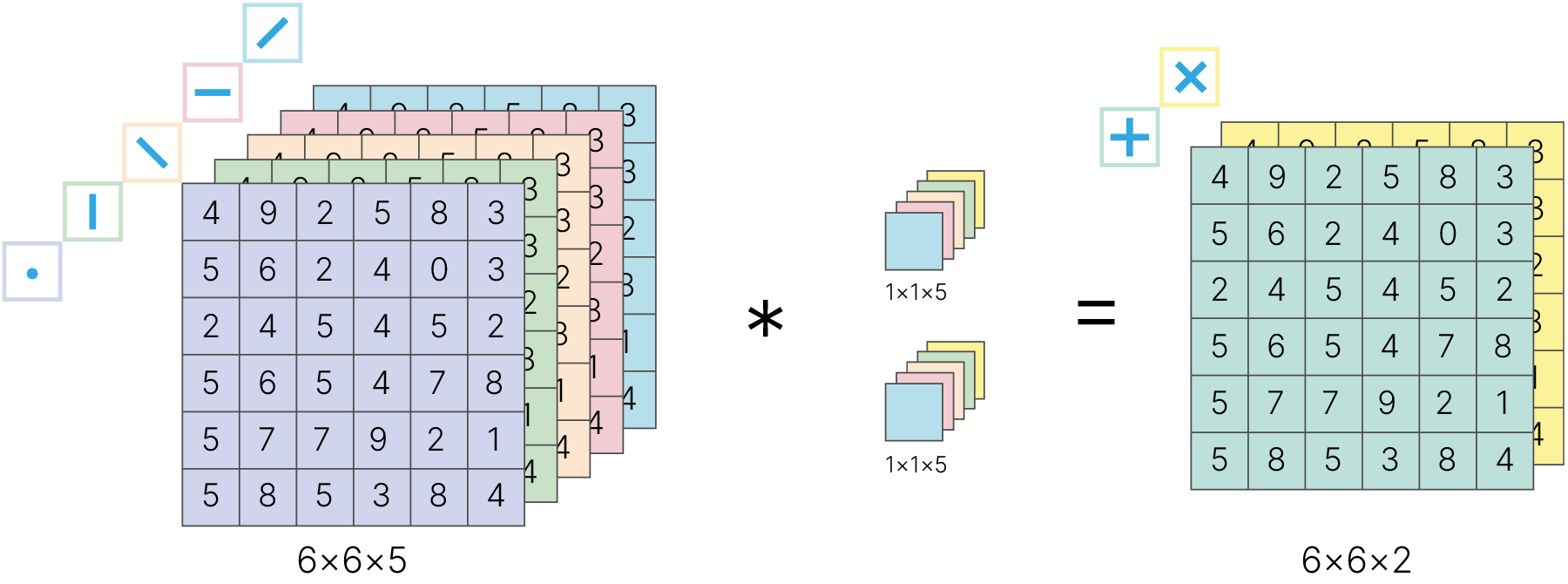
Фактически такая свертка — это линейный слой, на вход которому подали все признаки из одной точки входа.
Когда переводим цветное изображение в градации серого, мы делаем похожую операцию: складываем все каналы с коэффициентом $\displaystyle\frac{1}{3}$:
$\displaystyle \text{Brightness} = \frac{1}{3} R + \frac{1}{3} G + \frac{1}{3}B $

При этом количество таких фильтров $1\times1$ может быть произвольным. Обычно свертку $1\times1$ применяют для уменьшения числа каналов, но и обратная ситуация тоже возможна.
Ниже приведён пример применения такого фильтра с целью снижения количества карт признаков.
conv = torch.nn.Conv2d(
in_channels=64, # Number of input channels
out_channels=32, # Number of filters
kernel_size=1,
)
input = torch.randn((1, 64, 56, 56))
out = conv(input)
print("Input shape:", input.shape)
print("Shape after 1x1 conv:", out.shape) # [1, 32, 56, 56] batch, C_out, H_out, W_out
Input shape: torch.Size([1, 64, 56, 56]) Shape after 1x1 conv: torch.Size([1, 32, 56, 56])
Оба упомянутых выше метода позволяют сделать архитектуру сети не слишком глубокой путём быстрого увеличения рецептивного поля нейронов, что позволяет уменьшить число обучаемых параметров модели. Познакомимся с ещё одним способом уменьшения числа обучаемых параметров модели.
Рассмотрим фрагмент архитектуры CNN, состоящий из одного свёрточного слоя с размерами ядра свёртки $F_h\times F_w$ и некоторой активации (например, torch.nn.ReLU 🛠️[doc]):
Так как обучаемыми параметрами являются элементы ядра свёртки и сдвиг (bias), число таких параметров очень легко посчитать:
Теперь мы можем значительно уменьшить число обучаемых параметров, внеся небольшое изменение в рассмотренную архитектуру. Перед применением свёрточного слоя с размером ядра $F_h \times F_w$ мы можем расположить ещё один свёрточный слой с ядром свёртки из одного единственного пространственного элемента ($1 \times 1$), который будет предназначен для уменьшения числа карт признаков перед подачей последующему свёрточному слою без изменений пространственных размеров $H$ и $W$:
$$... \rightarrow (N, C_{in}, H, W) \rightarrow \text{conv2d}_{1 \times 1} \rightarrow \text{ReLU} \rightarrow (N, C_{mid}, H, W) \rightarrow \\ \rightarrow (N, C_{mid}, H, W) \rightarrow \text{conv2d}_{F_h\times F_w} \rightarrow \text{ReLU} \rightarrow (N, C_{out}, H', W') \rightarrow ... $$Идея заключается в следующем: рассматривая набор входных карт признаков $C_{in} \times (H \times W)$, можно выделить вектор размерностью $C_{in}$, содержащий элементы карт признаков с некоторыми фиксированными пространственными координатами. Элементы этого вектора сообщают, насколько сильно рецептивное поле соответствует каждому из $C_{in}$ шаблонов. Применение к входным картам признаков свёрточного слоя с ядром $1 \times 1 $ и последующей активации приведёт к нелинейному преобразованию таких векторов из пространства размерности $C_{in}$ в новое пространство размерности $C_{mid}$. Так как параметры такого сжимающего преобразования будут подбираться в процессе обучения, мы ожидаем, что свёртка $1 \times 1$ позволит подобрать полезные комбинации входных карт признаков для всех пространственных элементов.
Если выбрать $C_{mid} < C_{in}$, то общие число параметров модели действительно уменьшится:
$$ \text{n_params}[\text{conv2d}_{1 \times 1} \rightarrow \text{conv2d}_{F_h \times F_w}] = \\ = (C_{in}\cdot 1\cdot 1 + 1) \cdot C_{mid} + (C_{mid} \cdot F_{h} \cdot F_w + 1) \cdot C_{out} \approx \frac{C_{mid}}{C_{in}} \text{n_params}[\text{conv2d}_{F_h \times F_w}] $$Давайте оценим количество ресурсов, которое требуется для обработки одного изображения из CIFAR-10 при помощи сверточного и полносвязного слоя.
Пусть сверточный слой будет содержать $6$ фильтров размером $3 \times 3 $, padding = 1, stride = 1, а полносвязный — $6$ выходов (как если бы мы делали классификацию $6$-ти классов).
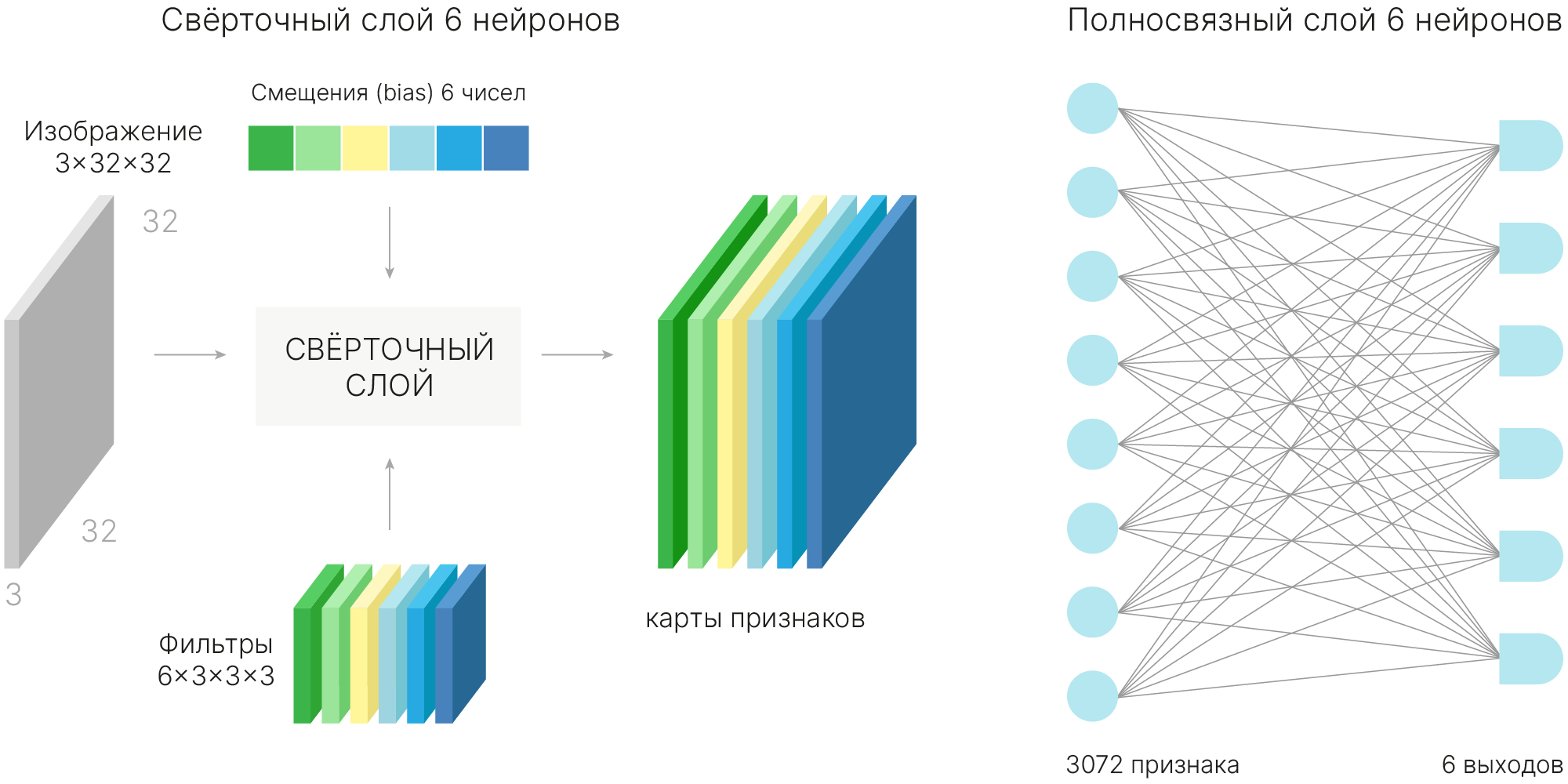
Количество параметров в одном фильтре: $C_{in}\times K_{h}\times K_{w} +1 = 3 \times 3 \times 3 + 1 = 28$
Количество фильтров $C_{out} = 6$
Итого: $(C_{in}\times K_{h}\times K_{w} +1) \times C_{out} = 28 \times 6 = 168$
from torch.nn import Conv2d
def get_params_count(module):
weights_count = 0
# Get all model weights: kernels + biases
for p in module.parameters():
print(p.shape)
# torch.prod - multiply all values in tensor
weights_count += torch.tensor(p.shape).prod()
print("Total weights", weights_count.item())
conv = Conv2d(3, 6, 3, bias=True)
get_params_count(conv)
torch.Size([6, 3, 3, 3]) torch.Size([6]) Total weights 168
Данные вытягиваем в вектор: $\text{inputs_count} = C_{in} \times H_{in} \times W_{in} = 3*32*32 = 3072$
Каждый нейрон (их $6$ шт.) выходного слоя хранит вес для каждого элемента входа ($3072$) и еще одно смещение: $\text{inputs_count} + 1) \times \text{outputs_count} = (3072 + 1) \times 6 = 18\ 438$
from torch.nn import Linear
linear = Linear(3072, 6, bias=True)
get_params_count(linear)
torch.Size([6, 3072]) torch.Size([6]) Total weights 18438
То есть для хранения весов такого линейного слоя нужно в $\approx 100$ раз больше памяти.
Считаем только умножения, т. к. (умножение + сложение = 1 FLOP 📚[wiki]).
В полносвязном слое каждый вход умножается на свой вес один раз, и количество умножений совпадает с количеством весов за вычетом сложения со смещением:
$C_{in} \times H_{in} \times W_{in} \times \text{outputs_count} = 3 \times 32 \times 32 \times 6 = 18\ 432 $
Разовое применение фильтра эквивалентно применению линейного слоя с таким же количеством весов:
$C_{in} \times K_{h} \times K_{w} \times C_{out} = 3 \times 3 \times 3 \times 6 = 162$
Т. е. умножаем каждый вес фильтра на вход.
$C_{in} \times K_{h} \times K_{w} \times C_{out} \times H_{out} \times W_{out} = 162 \times 30 \times 30 = 145\ 800 $
То есть количество операций в $\approx 10$ раз больше, чем у полносвязного слоя.
Выводы: выигрыш по количеству параметров при использовании свёрточного слоя омрачается большим количеством операций перемножения. Это было проблемой в течение долгого времени, пока вычисление операции свёртки не перевели на видеокарты (Graphical Processing Unit). При выполнении свёртки одного сегмента не требуется информация о результатах свёртки на другом сегменте, поэтому данные операции можно выполнять параллельно, с чем как раз прекрасно справляются видеокарты.
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = Conv2d(in_channels=1, out_channels=6, kernel_size=3)
model.to(device) # send model to device
dummy_input = torch.randn(1, 1, 5, 5)
out = model(dummy_input.to(device)) # send data to GPU too!
# ... do backprop if need
out = out.cpu() # move data back to main memory
Теперь мы можем более детально взглянуть на типичную архитектуру свёрточной нейронной сети. Как ранее уже обсуждалось, в первую очередь необходимо последовательностью свёрточных слоёв и уплотнений достичь того, чтобы каждый элемент карты активации имел большое рецептивное поле, а значит мог отвечать за большие и сложные шаблоны. Затем данные карты активаций выпрямляются в вектора и передаются в полносвязные слои, последовательность которых, используя глобальную информацию, возвращает значение целевой переменной.
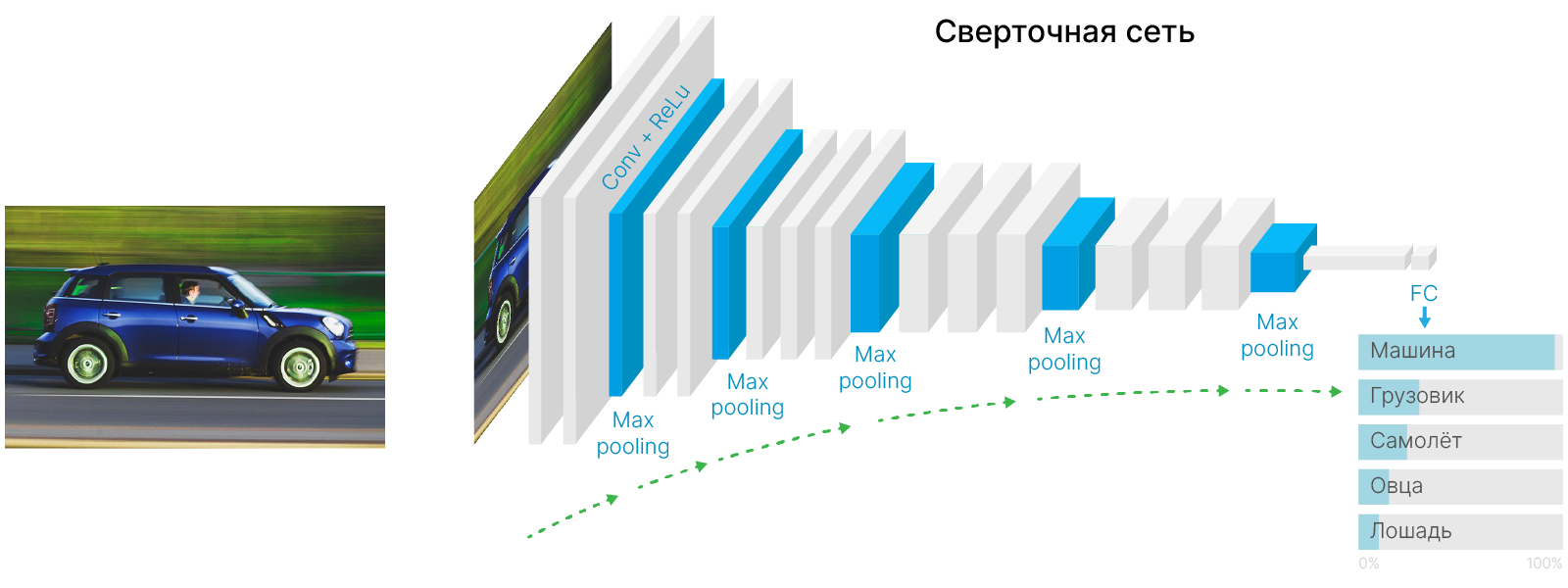
В результате количество признаков уменьшается от слоя к слою.
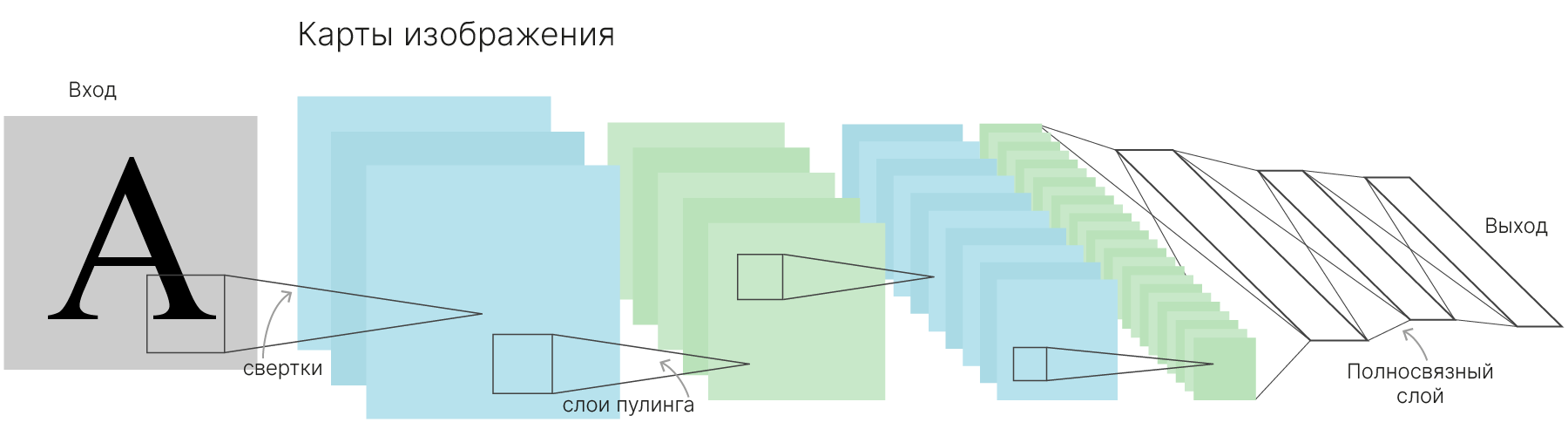
Примером сети, построенной по такой архитектуре, является LeNet. Она была разработана в 1989 г. Яном Ле Куном 📚[wiki]. Сеть имела 5 слоев с обучаемыми весами, из них 2 — сверточные.
Применялась в США для распознавания рукописных чисел на почтовых конвертах до начала 2000 г.
Процесс обучения почти не будет отличаться от обучения полносвязной сети. Такие же оптимизатор и функция потерь.
Сигнал, который мы обрабатываем при помощи сверточного слоя, не обязательно должен быть картинкой и не обязательно он должен быть двумерным.
В качестве примера такого сигнала может выступать звук:
import torchaudio
dataset = torchaudio.datasets.YESNO("./", download=True)
100%|██████████| 4.49M/4.49M [00:00<00:00, 38.1MB/s]
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 5))
waveform, sample_rate, label = dataset[0]
plt.plot(waveform.flatten())
plt.show()
В PyTorch одномерная свертка задается аналогично двумерной — torch.nn.Conv1d 🛠️[doc]:
torch.nn.Conv1d(in_channels, out_channels, kernel_size, stride=1, padding=0, ...)from torch import nn
conv = nn.Conv1d(1, 16, 3, stride=2)
output = conv(waveform)
print(output.shape)
torch.Size([16, 25399])
Но такой сигнал чаще преобразуют в спектрограмму, а к ней уже можно применить 2D-свёртку:
import librosa
from torchaudio.transforms import Spectrogram
spec_obj = Spectrogram(power=2, center=True, pad_mode="reflect")
spec = spec_obj(waveform[0])
plt.figure(figsize=(7, 5))
plt.imshow(librosa.power_to_db(spec))
plt.title("Spectrogram")
plt.xlabel("time")
plt.ylabel("freq")
plt.xticks([], [])
plt.yticks([], [])
plt.show()
Другим примером могут являться, например, спектрограммы растворов.
В работе Fluorescent multimodal nanosensorof heavy metal ions based on carbon dots исследовалась проблема контроля изменения содержания тяжелых металлов в жидких средах методом оптической спектроскопии. В качестве входных данных использовались спектрограммы растворов:
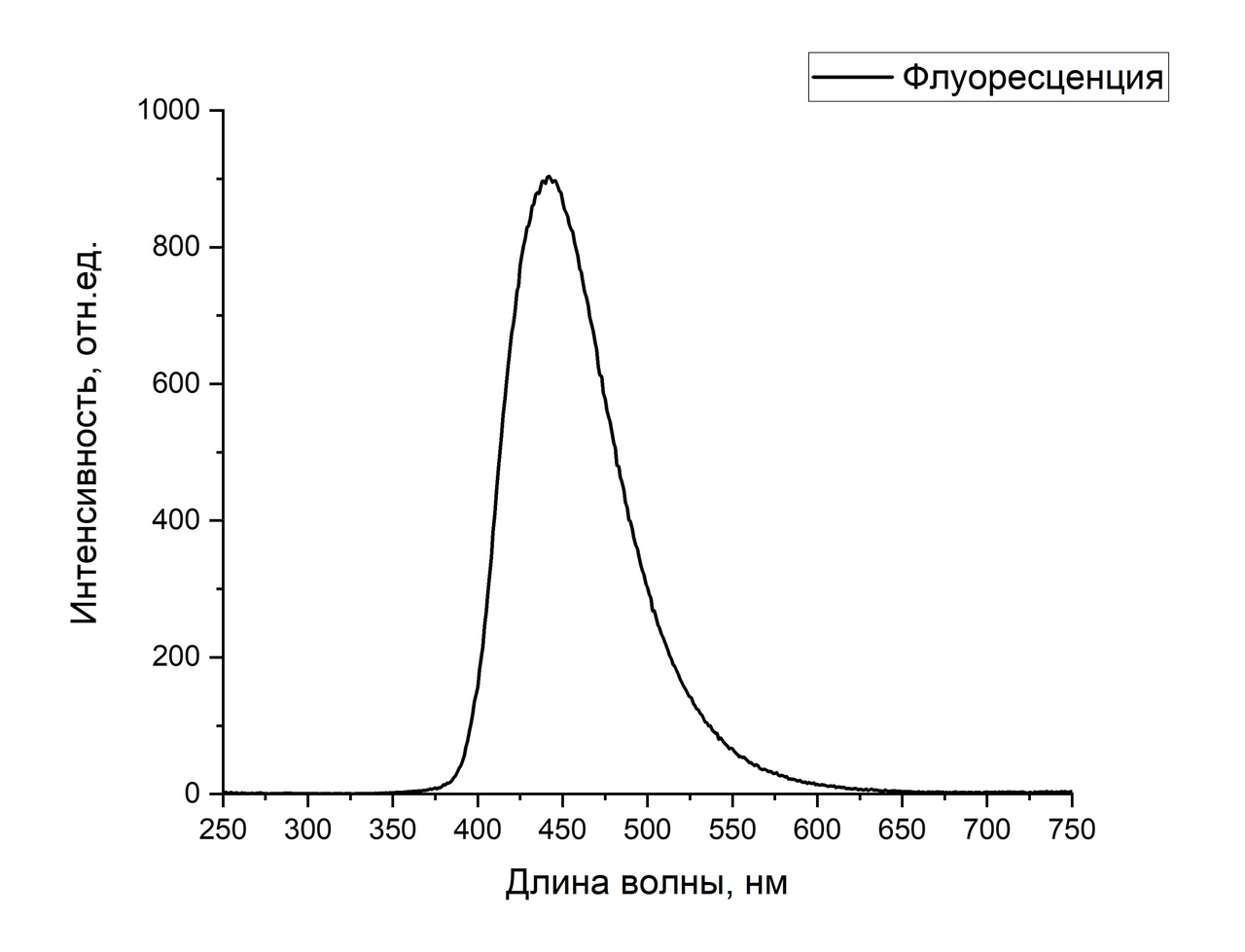
Если мы воздействуем на образец светом с разной длиной волны, а фиксируем суммарную интенсивность излучения, то для обработки таких данных можно использовать 1D-свёртку.
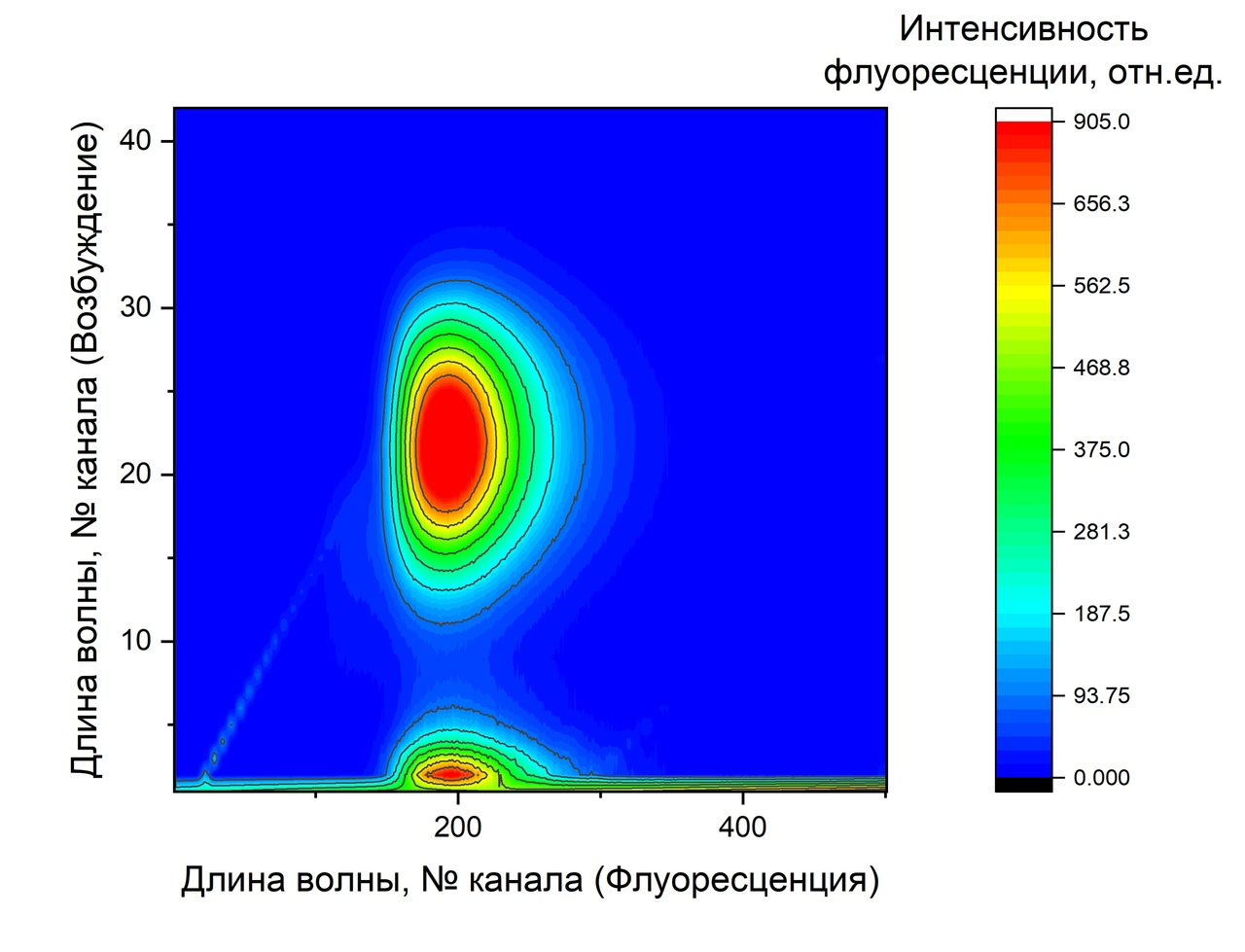
Если мы можем зафиксировать отклик на разных длинах волн, то используем 2D-свёртку
Рассмотрим, как выглядит операция свертки в функциональном анализе.
Есть две различные функции, определяющие локальную "схожесть" функций $f(t)$ и $g(t)$:
Взаимная корреляция более интуитивно понятна: она представляет собой "наложение" шаблона на функцию, а свертка — "наложение" отраженного шаблона. Эти функции взаимосвязаны: $$f(t) ⋆ g(t) = f(-t) * g(t)$$
Можно представить свертку как площадь произведения двух функций внутри скользящего окна, как на анимации ниже.
В машинном обучении под словом convolution как правило подразумевают взаимнокорреляционную функцию ✏️[blog], а не свертку. В реальности при обучении нейронной сети совершенно неважно, используется ли свертка или взаимнокорреляционная функция — они отличаются лишь порядком расположения весов внутри тензора ядра.
В случае дискретных величин для вычисления взаимной корреляции сигнал $f(t)$ поэлементно умножается со смещенным ядром $g(t)$, и результат суммируется:
$$\large(f \star g)(t) = f(1)g(t+1) + f(2)g(t+2) + f(3)g(t+3) + ...$$Одномерная операция свертки используется для данных, имеющих последовательную структуру: текстов, аудиозаписей, цифровых сигналов. Как правило, такую структуру можно представить в виде изменения величины с течением времени.
Данные связаны в одном измерении — временном. Их тоже можно обработать при помощи свертки, но уже в одном измерении.
Проводить вычисления при помощи вложенных циклов малоэффективно. Но операцию свертки можно реализовать через матричное умножение, которое очень эффективно выполняется на GPU
Для двумерной свертки действует похожая логика, подробне можно прочесть здесь:
[blog] ✏️ 2D Convolution as a Matrix-Matrix Multiplication
И при получении градиентов это тоже работает:
[blog] ✏️ Forward and Backward Convolution Passes as Matrix Multiplication
Двумерная операция свертки, о которой мы много говорили, применяется для обработки данных, имеющих пространственную структуру, то есть тех данных, для которых играют роль взаимные расположения по двум осям. Совсем не обязательно, чтобы эти оси соответствовали высоте и ширине картинки. Например, одна ось может соответствовать координате сенсора в одномерной матрице, а вторая — времени получения информации с него.
Трёхмерная операция свертки используется, когда данные имеются три независимых "пространственных" компоненты.
Простейшим примером являются видео: к двумерной структуре самих изображений добавляется координата времени.
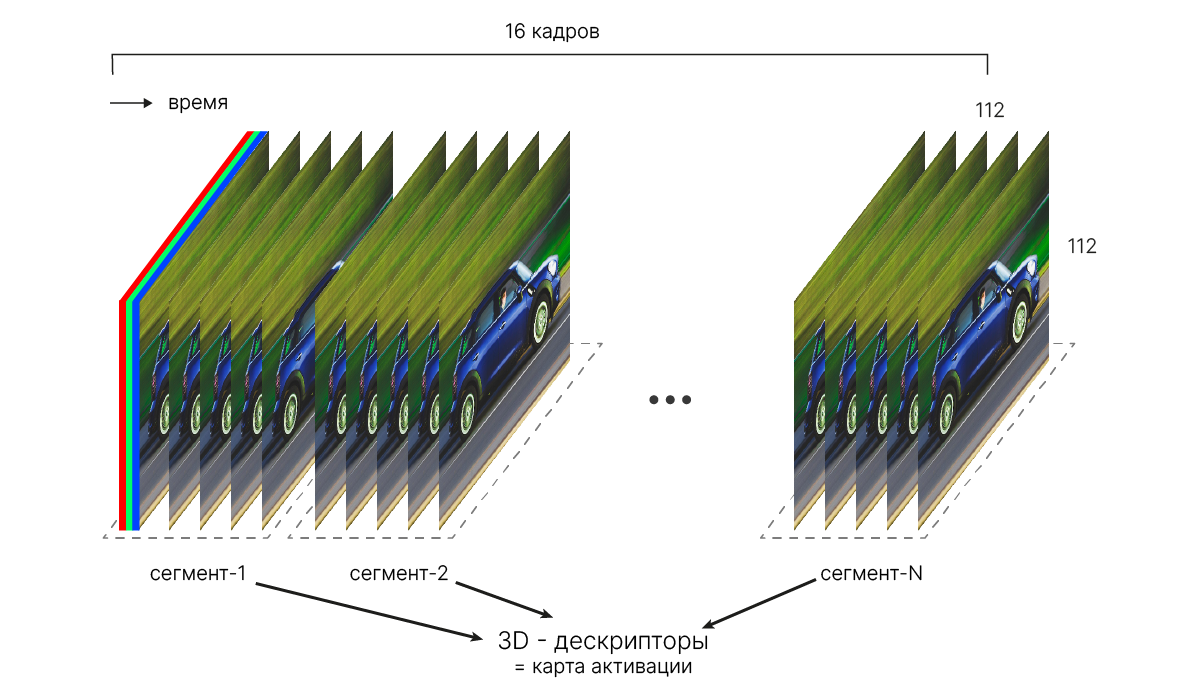
torch.nn.Conv3d(in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros')import torch
# With cubic kernels and same stride
conv = nn.Conv3d(in_channels=16, out_channels=33, kernel_size=3, stride=2)
# non-square kernels with unequal stride and padding
conv = nn.Conv3d(
in_channels=16,
out_channels=33,
kernel_size=(3, 5, 2),
stride=(2, 1, 1),
padding=(4, 2, 0),
)
input = torch.randn(20, 16, 10, 50, 100)
out = conv(input)
print("out shape: ", out.shape)
out shape: torch.Size([20, 33, 8, 50, 99])
Другой популярный тип 3D-данных — это медицинские снимки (KT, МРТ). Для их хранения используются специальные форматы (NIFTI ✏️[blog], DICOM 📚[wiki]).
Для работы с ними существуют специальные библиотеки. Воспользуемся одной из них — библиотекой NiBabel 🛠️[doc], чтобы преобразовать файл из формата NIFTI в 3D-массив. Для этого скачаем образец МРТ мозга:
# !wget -q https://nipy.org/nibabel/_downloads/f76cc5a46e5368e2c779868abc49e497/someones_epi.nii.gz
!wget -q https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/someones_epi.nii.gz
И откроем его при помощи NiBabel:
import nibabel as nib
epi_img = nib.load("someones_epi.nii.gz")
epi_img_data = epi_img.get_fdata()
print(epi_img_data.shape)
print("Max", epi_img_data.max(), "Min", epi_img_data.min())
(53, 61, 33) Max 103.76662158966064 Min 7.742551803588867
Можно воспринимать этот массив как набор черно-белых изображений.
import numpy as np
def show_slices(ax, data):
slices = np.linspace(0, len(data) - 1, num=10).astype(int)
for i, sl in enumerate(slices):
ax[i].axis("off")
ax[i].imshow(data[sl], cmap="gray", origin="lower")
fig, axes = plt.subplots(3, 10, figsize=(16, 4))
show_slices(axes[0], epi_img_data)
show_slices(axes[1], np.moveaxis(epi_img_data, 0, 1))
show_slices(axes[2], np.moveaxis(epi_img_data, 0, 2))
plt.show()
Преобразуем массив в torch.Tensor. При этом добавим размерность для каналов:
import torch
brain_mrt = torch.Tensor(epi_img_data)
brain_mrt = brain_mrt.unsqueeze(0) # add channel dim
print("Add channel dim", brain_mrt.shape)
Add channel dim torch.Size([1, 53, 61, 33])
Теперь можно подать его на вход Conv3d:
from torch import nn
conv3d = nn.Conv3d(
in_channels=1,
out_channels=16,
kernel_size=(3, 3, 3),
stride=(1, 1, 1),
padding=(1, 1, 1),
)
out = conv3d(brain_mrt.unsqueeze(0)) # add batch dim and run inference
print("out shape: ", out.shape)
out shape: torch.Size([1, 16, 53, 61, 33])
Некоторые данные естественно хранить в виде графа:
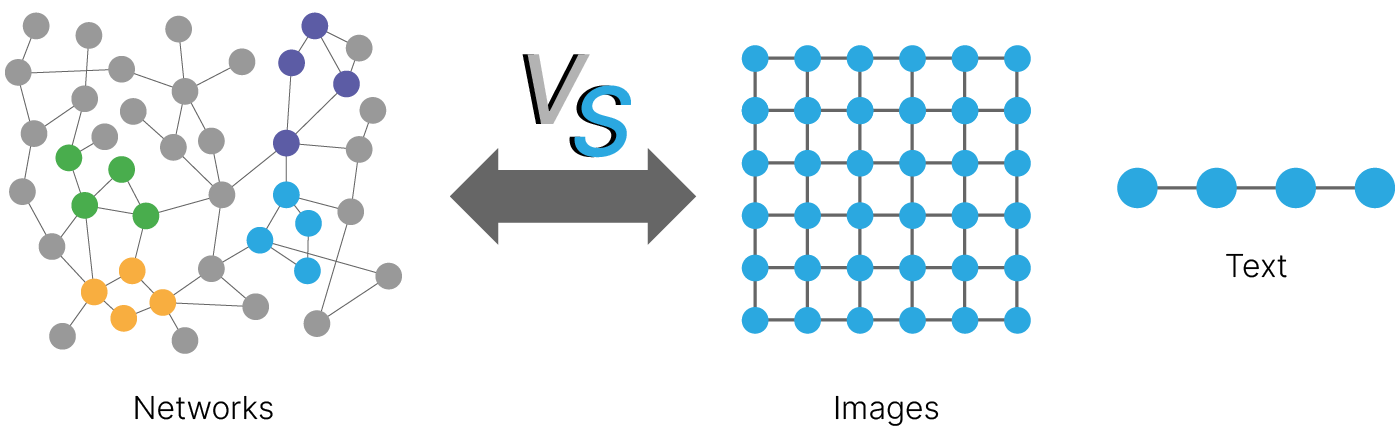
Для работы с графами можно использовать пакет PyTorch Geometric 🛠️[doc]. Установим его:
!pip install -q torch_geometric
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 1.1/1.1 MB 12.9 MB/s eta 0:00:00
Создадим простой граф для демонстрации. Сначала создаем список вершин. Для простоты каждая вершина будет содержать одно число. Но в общем случае вершина может содержать любую информацию, чаще в виде вектора чисел. Размер эмбеддингов у всех вершин графа должен совпадать.
import torch
x = torch.tensor([[0], [1], [2], [3], [4], [5]], dtype=torch.float)
Ребра между вершинами можно задать:
в виде матрицы связанности (adjacency matrix 📚[wiki]);
в виде списка пар вершин, между которыми есть ребра (COO 🛠️[doc] of coordinate list format).
Второй способ компактнее, воспользуемся им. Число в первой строке — это номер исходящей вершины, число во второй (с тем же индексом) — номер входящей.
# fmt: off
edge_index = torch.tensor([[0, 1, 2, 2, 3, 4, 4],
[1, 2, 3, 4, 5, 2, 5]], dtype=torch.long)
# fmt: on
В PyTorch Geometric для работы с графами используется класс Data 🛠️[doc]. Инициализируем экземпляр этого класса списком вершин и ребер.
from torch_geometric.data import Data
data = Data(x=x, edge_index=edge_index)
data.validate(raise_on_error=True) # optional check
True
Для визуализации созданного графа используем пакет NetworkX 🛠️[doc]. Он совместим с PyTorch Geometric 🛠️[doc]
[doc] 🛠️ Drawing — basic functionality for visualizing graphs
import networkx as nx
from torch_geometric.utils import to_networkx
nx.draw(to_networkx(data, to_undirected=False))
Нам понадобится код для визуализации, поэтому поместим его в функцию:
import networkx as nx
import matplotlib.pyplot as plt
from torch_geometric.utils import to_networkx
from networkx.drawing.layout import kamada_kawai_layout
def show_graph(graph, colors=None, embeddings=False):
fs = 14
int2label = {}
g = to_networkx(graph, to_undirected=False) #
if embeddings:
for i, e in enumerate(graph.x):
str_emb = ["{0:0.1f}".format(p.item()) for p in e]
int2label[i] = f"{i}: [" + ",".join(str_emb) + "]"
g = nx.relabel_nodes(g, int2label)
fs = 10
plt.axis("off")
nx.draw_networkx(
g,
pos=kamada_kawai_layout(
g, dim=2, scale=1, center=None
), # nx.spring_layout(G, seed=0),
with_labels=True,
node_size=800,
node_color=colors, # data.y, for clustering
# cmap="hsv",
# vmin=-2,
# vmax=3,
# width=0.8,
edge_color="grey",
font_size=fs,
)
На графах тоже можно выполнять операцию свертки. Разберем классический алгоритм из статьи Semi-Supervised Classification with Graph Convolutional Networks 🎓[arxiv].
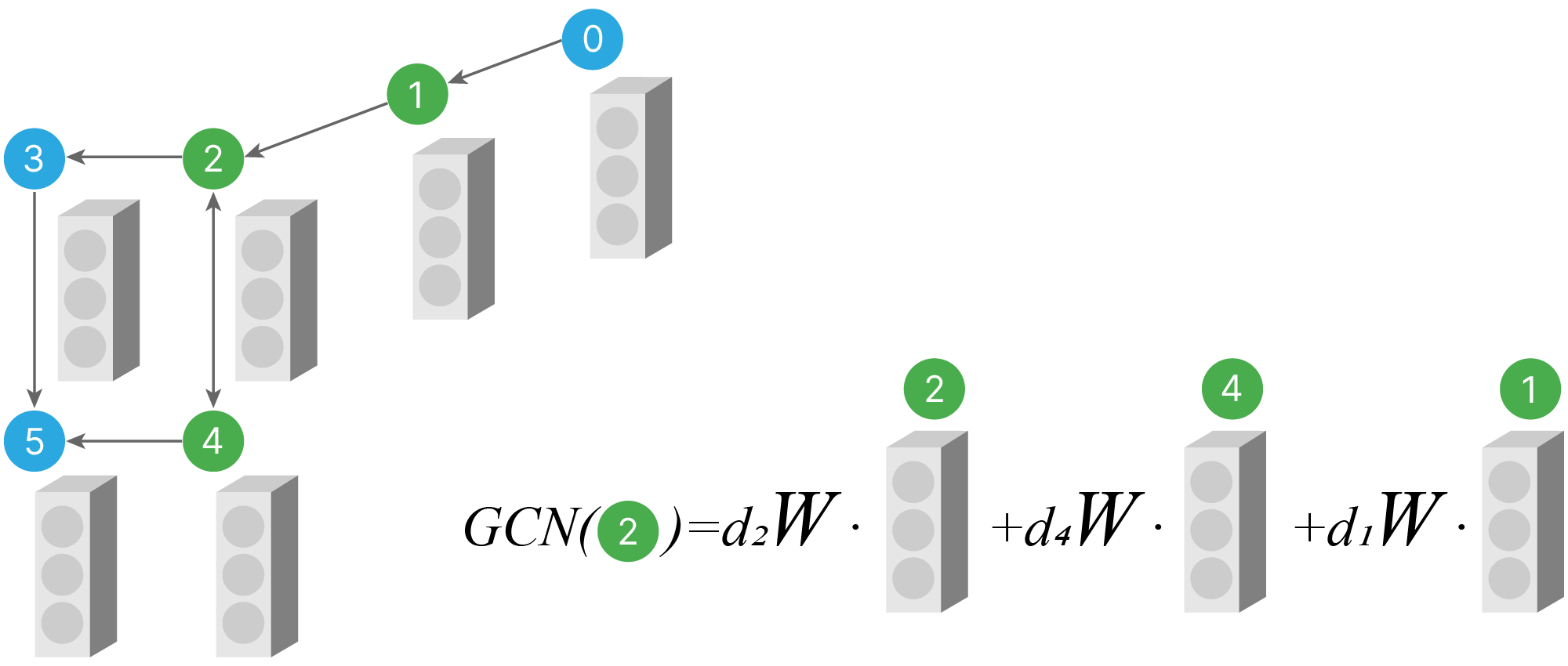
На выходе у графового сверточного слоя новые эмбеддинги для всех вершин. Новый эмбеддинг считается как взвешенная сумма скалярных произведений эмбеддингов соседних вершин на матрицу весов.
Это напоминает свертку $1\times1$ для изображений с последующим пулингом. Основное отличие в том, что количество соседей у разных вершин может отличаться, и в сумме будет получаться разное количество слагаемых. Поэтому необходимо их взвесить (множители $d_i$ на картинке.). Если все $d_i = 1$, то графовая свертка вычисляется по той же формуле:
$$\large y_i = \sum_{i \in N} x_i*W,$$где $N$ — множество номеров соседей $i$-той вершины,
$x_i$ — эмбеддинг $i$-той вершины,
$W$ — матрица весов, одна для всех вершин.
Вот как выглядят соседи каждой вершины, которые будут участвовать в свертках. Соседняя вершина — эта та, из которой есть путь в рассматриваемую.
plt.figure(figsize=(30, 4))
plt.subplot(1, 6, 1).set_title("GC Node0")
show_graph(data, ["green", "gray", "gray", "gray", "gray", "gray"])
plt.subplot(1, 6, 2).set_title("GC Node1")
show_graph(data, ["lightgreen", "green", "gray", "gray", "gray", "gray"])
plt.subplot(1, 6, 3).set_title("GC Node2")
show_graph(data, ["gray", "lightgreen", "green", "gray", "lightgreen", "gray"])
plt.subplot(1, 6, 4).set_title("GC Node3")
show_graph(data, ["gray", "gray", "lightgreen", "green", "gray", "gray"])
plt.subplot(1, 6, 5).set_title("GC Node4")
show_graph(data, ["gray", "gray", "lightgreen", "gray", "green", "gray"])
plt.subplot(1, 6, 6).set_title("GC Node5")
show_graph(data, ["gray", "gray", "gray", "lightgreen", "lightgreen", "green"])
В PyTorch Geometric графовый сверточный слой реализуется классом GCNConv🛠️[doc]:
from torch_geometric.nn import GCNConv
gcn = GCNConv(in_channels=1, out_channels=3)
print(gcn)
GCNConv(1, 3)
in_channels — это размерность эмбеддинга вершины на входе, а out_channels — на выходе.
for name, p in gcn.named_parameters():
print(name, p.shape)
bias torch.Size([3]) lin.weight torch.Size([3, 1])
Фактически out_channels — это количество столбцов в матрице $W$.
Посмотрим, как работает слой.
Поскольку нам нужны эмбеддинги, заменим значения $x$, которые были просто равны номеру вершины, на one_hot вектора:
from torch.nn.functional import one_hot
embeddings = one_hot(x.flatten().long()).float()
data = Data(x=embeddings, edge_index=edge_index)
data.validate(raise_on_error=True)
show_graph(data, embeddings=True)
print(embeddings)
tensor([[1., 0., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 0.],
[0., 0., 0., 1., 0., 0.],
[0., 0., 0., 0., 1., 0.],
[0., 0., 0., 0., 0., 1.]])
Создадим графовую свертку с одним нейроном средствами PyTorch Geometric. Для начала отключим все дополнительные опции и инициализируем веса единицами, чтобы было проще понять, как она работает.
gcn = GCNConv(len(x), 1, add_self_loops=False, bias=False, normalize=False)
gcn.lin.weight.data = torch.ones((1, len(x)))
print(gcn, " weights ", gcn.lin.weight)
GCNConv(6, 1) weights Parameter containing: tensor([[1., 1., 1., 1., 1., 1.]], requires_grad=True)
out = gcn(embeddings, edge_index)
print(out) # Embedding (dim=1) for every node from 0 ... 5
tensor([[0.],
[1.],
[2.],
[1.],
[1.],
[2.]], grad_fn=<ScatterAddBackward0>)
Эта операция соответствует перемножению эмбеддингов вершин на веса и сумму по всем соседям:
$$\large y_i = \sum_{j \in N_i} \bar x_j \cdot \bar w,$$$N_i$ — это множество соседей $i$-й вершины, соседи — это вершины, из которых есть путь в текущую.
Проделаем ее самостоятельно. Эмбеддинг каждой вершины умножается на одну и ту же матрицу весов:
y = embeddings @ gcn.lin.weight.data.T
print(y)
tensor([[1.],
[1.],
[1.],
[1.],
[1.],
[1.]])
show_graph(Data(x=y, edge_index=edge_index), embeddings=True)
Полученные после перемножения результы суммируются для соседей каждой вершины.
В PyTorch Geometric эта операция реализуется пакетом torch_scatter 🛠️[doc].
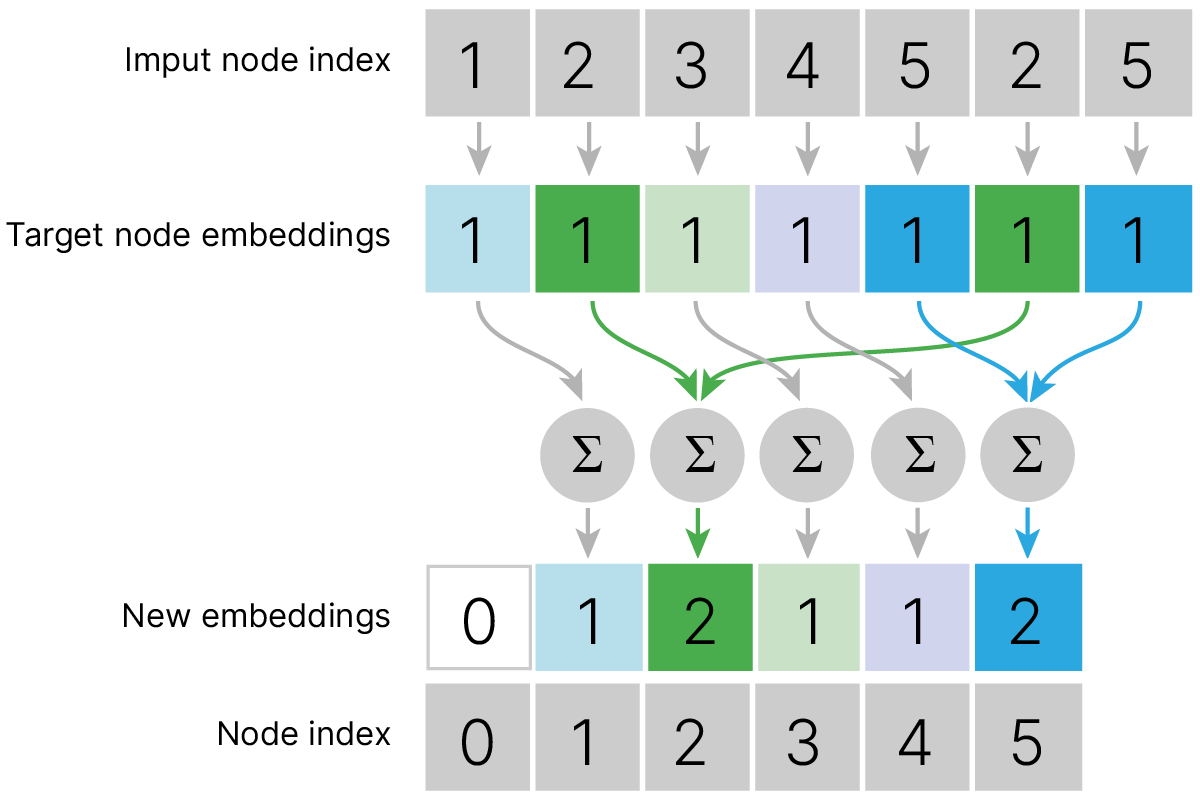
oc = torch.zeros_like(y) # out custom
oc[0] = 0 # no nighbors
oc[1] = y[0] # one neighbor (#0)
oc[2] = y[1] + y[4]
oc[3] = y[2]
oc[4] = y[2]
oc[5] = y[3] + y[4]
print(oc)
assert torch.allclose(out, oc)
tensor([[0.],
[1.],
[2.],
[1.],
[1.],
[2.]])
show_graph(Data(x=oc, edge_index=edge_index), embeddings=True)
Улучшения
Логично добавлять к сумме эмбеддинг самой вершины.
Для этого нужно либо в edge_index добавить к каждой вершине путь в саму себя, либо установить параметр конструктора GCNConv add_self_loops = True, тогда
$x_i \in N_i$
Число соседей у разных вершин может сильно отличаться, и результат графовой свертки для вершины с одним соседом по абсолютному значению будет сильно меньше, чем для вершины, у которой $200$ соседей. Поэтому логично нормировать выходы на количество слагаемых (число соседей вершины). Количество соседей вершины обозначим как : $deg(i) = d_i$, тогда:
Чтобы порядок значений сохранялся, добавили корень. Теперь при $d_i == d_j$ значения $(2)$ и $(3)$ будут равны.
У ребер могут быть собственные веса, задающие силу связи между вершинами. Их можно добавить при прямом проходе, используя параметр edge_weight метода GCNConv.forward. По умолчанию эти веса равны $1$, обозначим их как $e_{j,i}$ .
Ослабление или усиление связи между вершинами означает изменение степени соседства. Поэтому $\displaystyle d_i = 1+\sum_{j \in N_i} e_{j,i} $, и общая формула примет вид:
$$\large y_i = \sum_{j \in N_i} \frac { e_{j,i} \bar x_j \cdot \bar w} {\sqrt {d_i d_j} } \quad(4)$$
Чтобы включить в сумму эмбеддинг самой вершины, надо передать в конструктор GCNConv параметр add_self_loops=True , а чтобы добавить нормировки на количество соседей, надо установить normalize=True
* Без установки normalized=True установка add_self_loops=True работает некорректно
gcn = GCNConv(len(x), 1, add_self_loops=True, bias=False, normalize=True)
gcn.lin.weight.data = torch.ones((1, len(x)))
out = gcn(embeddings, edge_index)
print(out)
tensor([[1.0000],
[1.2071],
[1.1498],
[0.9082],
[0.9082],
[1.1498]], grad_fn=<ScatterAddBackward0>)
show_graph(Data(x=out, edge_index=edge_index), embeddings=True)
В коде это могло бы выглядеть примерно так:
from math import sqrt
def get_neighbors(n):
# find all neighbors of node n
neighbors = [n] # first put to neighbors list index of node itself
for i, node_num in enumerate(edge_index[1]):
if node_num == n:
neighbors.append(edge_index[0][i].item())
return neighbors
out_norm = torch.zeros_like(out) # final summ
for i, e in enumerate(y):
neighbors = get_neighbors(i)
deg_i = len(neighbors) # neighbors count of node i
for node_num in neighbors:
deg_j = len(
get_neighbors(node_num)
) # neighbors count of j-th neighbor of node i
out_norm[i] += y[node_num] / (
sqrt(deg_i) * sqrt(deg_j)
) # Implementation of equation (3)
print(out_norm)
assert torch.allclose(out, out_norm) # check that results of CGNConv the same
tensor([[1.0000],
[1.2071],
[1.1498],
[0.9082],
[0.9082],
[1.1498]])
Добавление весов к ребрам:
print(edge_index)
tensor([[0, 1, 2, 2, 3, 4, 4],
[1, 2, 3, 4, 5, 2, 5]])
edge_weight = torch.Tensor([1, 1, 1, 1, 1, 1, 20]) # increase 4->5 edge weight
out = gcn(embeddings, edge_index, edge_weight)
print(["{0:0.2f}".format(i.item()) for i in out])
show_graph(Data(x=out, edge_index=edge_index), embeddings=True)
['1.00', '1.21', '1.15', '0.91', '0.91', '3.21']
Если мы добавим в слой ещё нейроны, то размерность эмбеддингов на выходе увеличится:
gcn = GCNConv(len(x), 8, add_self_loops=True, bias=False, normalize=True)
out = gcn(embeddings, edge_index)
show_graph(Data(x=out, edge_index=edge_index), embeddings=True)
Это имеет смысл, так как эмбеддинг должен вобрать в себя информацию о соседних вершинах, и, чтобы закодировать ее, требуется место. А если мы объединим несколько слоев вместе, то можем добиться того, что каждый эмбеддинг сможет содержать информацию о всех доступных вершинах.
from torch_geometric.nn import GCNConv
class GCN(torch.nn.Module):
def __init__(self):
super().__init__()
self.gcn1 = GCNConv(6, 8)
self.gcn2 = GCNConv(8, 16)
def forward(self, x, edge_index, batch_index=None):
x = self.gcn1(x, edge_index).relu()
return self.gcn2(x, edge_index)
model = GCN()
print(model)
GCN( (gcn1): GCNConv(6, 8) (gcn2): GCNConv(8, 16) )
out = model(embeddings, edge_index)
print(out.shape)
# show_graph(Data(x = out, edge_index=edge_index), embeddings =True)
torch.Size([6, 16])
С каждым слоем количество соседей, которое участвует в получении эмбеддинга вершины, будет расти. Можно сравнить это с увеличением рецептивного поля нейрона в обычной сверточной сети. Вот пример того, как будет расти рецептивное поле 3-й вершины с увеличением числа слоев:
plt.figure(figsize=(15, 4))
plt.subplot(1, 3, 1).set_title("GC Node3 Layer 0")
show_graph(data, ["gray", "gray", "lightgreen", "green", "gray", "gray"])
plt.subplot(1, 3, 2).set_title("GC Node3 Layer 1")
show_graph(data, ["gray", "lightgreen", "lightgreen", "green", "lightgreen", "gray"])
plt.subplot(1, 3, 3).set_title("GC Node3 Layer 3")
show_graph(
data, ["lightgreen", "lightgreen", "lightgreen", "green", "lightgreen", "gray"]
)
На выходе CGNConv-слоя мы получаем граф с новыми эмбеддингами. Его можно использовать для решения ряда задач:
Чтобы лучше понять, как работают сверточные сети, можно визуализировать карты активаций и веса фильтров свёртки.
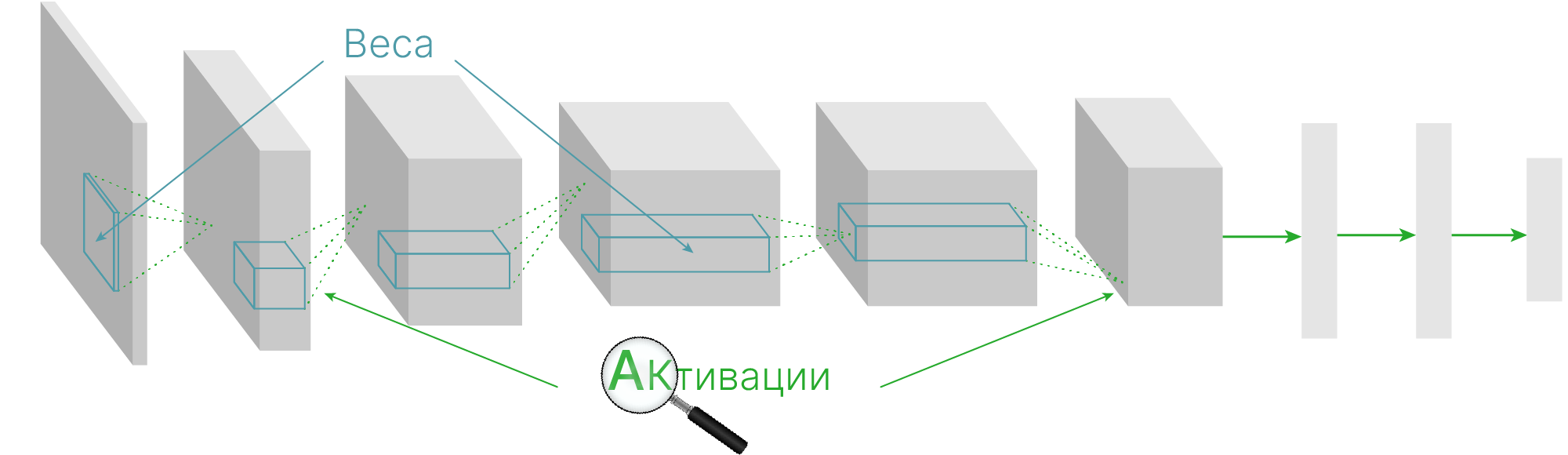
Веса фильтров на первом слое легко визуализировать. И результат легко интерпретируется, так как у фильтров такое же количество каналов, как и у цветных изображений ($3$ канала).
Ниже приведен пример того, как это можно сделать для обученной модели AlexNet из зоопарка моделей torchvision.
Чтобы понять, через какие свойства можно получить доступ к весам, выведем структуру модели
from torchvision import models
alexnet = models.alexnet(weights="AlexNet_Weights.DEFAULT")
print(alexnet)
Downloading: "https://download.pytorch.org/models/alexnet-owt-7be5be79.pth" to /root/.cache/torch/hub/checkpoints/alexnet-owt-7be5be79.pth 100%|██████████| 233M/233M [00:01<00:00, 123MB/s]
AlexNet(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(11, 11), stride=(4, 4), padding=(2, 2))
(1): ReLU(inplace=True)
(2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(3): Conv2d(64, 192, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(4): ReLU(inplace=True)
(5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Conv2d(192, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(7): ReLU(inplace=True)
(8): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(9): ReLU(inplace=True)
(10): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): ReLU(inplace=True)
(12): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(avgpool): AdaptiveAvgPool2d(output_size=(6, 6))
(classifier): Sequential(
(0): Dropout(p=0.5, inplace=False)
(1): Linear(in_features=9216, out_features=4096, bias=True)
(2): ReLU(inplace=True)
(3): Dropout(p=0.5, inplace=False)
(4): Linear(in_features=4096, out_features=4096, bias=True)
(5): ReLU(inplace=True)
(6): Linear(in_features=4096, out_features=1000, bias=True)
)
)
Видно, что первый слой — это $0$-й элемент контейнера features.
Веса слоя хранятся в weight.data.
weight_tensor = alexnet.features[0].weight.data # extract weights
print("Weights shape", weight_tensor.shape)
Weights shape torch.Size([64, 3, 11, 11])
from torchvision import utils
img_grid = utils.make_grid(
(weight_tensor + 1) / 2, pad_value=1
) # combine weights from all channel into table, note remapping to (0,1) range
print("Output is CxHxW image", img_grid.shape)
Output is CxHxW image torch.Size([3, 106, 106])
make_grid часто используют, чтобы отображать изображения в TensorBoard.
А чтобы отобразить получившуюся таблицу в блокноте средствами matplotlib, нам потребуется поменять порядок хранения данных, поместив каналы на первое место.
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (8, 8)
plt.imshow(
np.transpose(img_grid, (1, 2, 0))
) # change channel order for compability with numpy & matplotlib
plt.show()
Видно, что модель научилась улавливать простые геометрические формы: края под разными углами, точки того или иного цвета. Фильтры AlexNet'а оказались настолько большими, что частично захватили не только простую локальную информацию, но и сложные градиенты или решётки.
К сожалению, выполнить ту же операцию для фильтров на скрытых слоях едва ли представляется разумным: в отличие от трёхканальных фильтров первого слоя, веса которых легко визуализировать, фильтры поздних слоёв имеют гораздо больше каналов, что затрудняет их визуализацию. Пожалуй, единственным вариантом является поканальное отображение весов, которое довольно сложно трактовать. Убедимся в этом, на примере ниже.
Higher Layer: Visualize Filter

Визуализируем веса $2$-го сверточного слоя AlexNet.
Слой доступен через features[3]
weights_of_conv2_layer = alexnet.features[3].weight.data # extract weights
print(weights_of_conv2_layer.shape)
torch.Size([192, 64, 5, 5])
В нем $192$ фильтра, в каждом $64$ ядра. Поэтому ограничимся первым фильтром и выведем все его ядра.
first_filter_kernels = weights_of_conv2_layer[0]
print(first_filter_kernels.shape)
torch.Size([64, 5, 5])
Чтобы использовать image_grid, входной тензор должен иметь формат $(B \times C \times H \times W)$. Поэтому добавим размерность, соответствующую каналам:
img_grid = utils.make_grid(
weights_of_conv2_layer[0].unsqueeze(1), pad_value=1 # add fake channel dim
)
plt.rcParams["figure.figsize"] = (8, 8)
plt.imshow(
np.transpose((img_grid + 1) / 2, (1, 2, 0))
) # change channel order for compability with numpy
plt.show()
Интерпретация такой визуализации довольно затруднительна, зато мы разобрались, как получать доступ к весам.
Наиболее очевидный метод визуализации заключается в том, чтобы показать активации сети во время прямого прохода. Для сетей ReLU активации обычно начинают выглядеть относительно сгущенными и плотными, но по мере развития обучения активации обычно становятся более редкими и локализованными.
На последних слоях свёрточной нейронной сети размеры рецептивных полей нейронов становятся сравнимы с размером исходного изображения, поэтому при визуализации их карт активации становится понятно, какие нейроны реагируют на какие части изображений.
К примеру, на изображении ниже активация выделенного нейрона достигнута благодаря пикселям, примерно соответствующим расположению лица человека, поэтому можно предположить, что он научился находить лица на изображении. Более подробно об этом можно почитать в статье Understanding Neural Networks Through Deep Visualization 🎓[arxiv].
Visualizing Activations
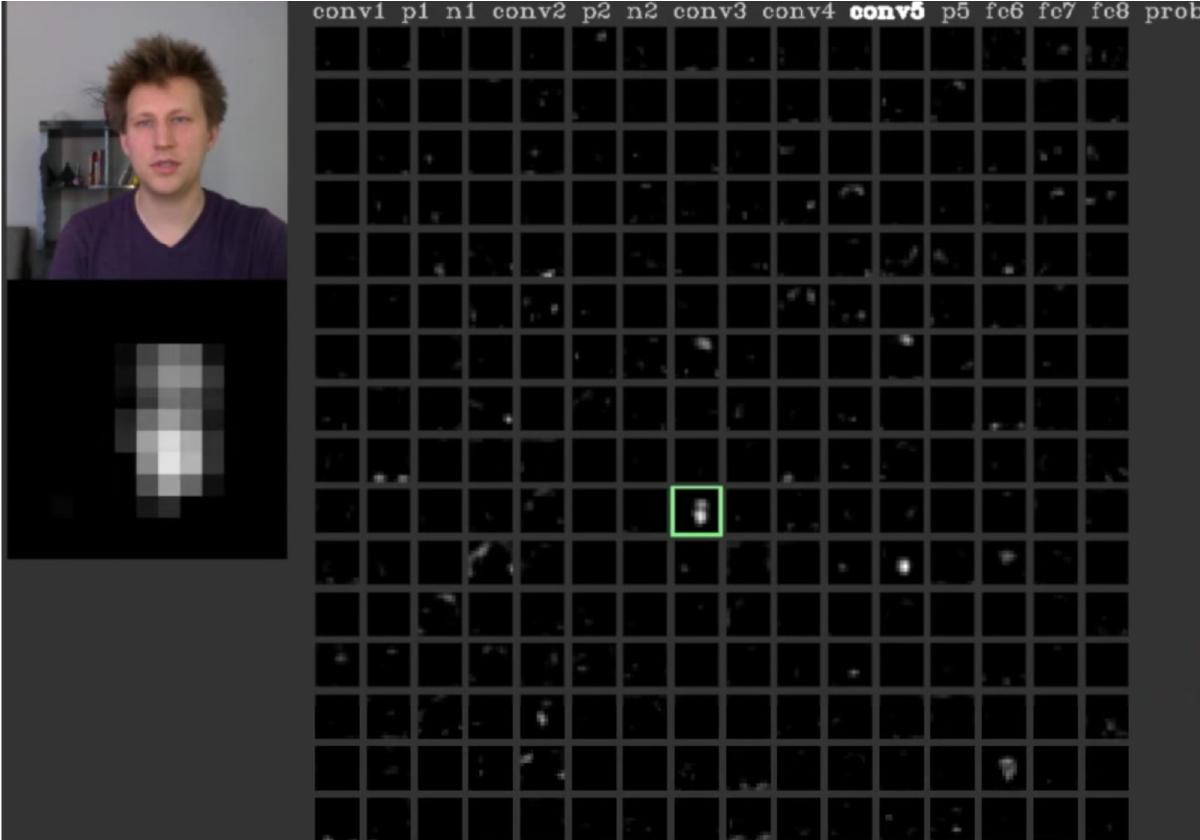
В отличие от весов, карты активаций не сохраняются в памяти. Для того, чтобы получить к ним доступ, в PyTorch предусмотрен механизм под названием Hooks 🛠️[doc].
Благодаря ему можно получить доступ к выходам или входам слоя как при прямом, так и при обратном распространении сигнала через сеть.
Зарегистрируем свой hook. Он просто выведет в консоль размеры карты активации (выхода слоя).
from torch import nn
def module_hook(module: nn.Module, input, output): # For nn.Module objects only.
print("Hi, i am hook_1 ! ", output.shape) # activation_map
handle = alexnet.features[10].register_forward_hook(
module_hook
) # attach hook to last conv layer
Проверим, что он работает:
import torch
out = alexnet(torch.randn(1, 3, 224, 224))
Hi, i am hook_1 ! torch.Size([1, 256, 13, 13])
Чтобы удалить hook, используйте метод remove дескриптора, который возвращает метод register_forward_hook:
handle.remove()
out = alexnet(torch.randn(1, 3, 224, 224))
Вывода нет, hook отключился!
Теперь напишем hook, который выведет нам карту активации.
Так как на выходе данного слоя $256$ каналов, выведем каждый отдельно, подав на вход make_grid тензор с $256$ элементами.
Для этого потребуется:
def module_hook(module: nn.Module, input, output):
# activation_map = output.squeeze(0).unsqueeze(1) # alternative solution
activation_map = output.permute(1, 0, 2, 3) # B <--> C
print(activation_map.shape)
img_grid = utils.make_grid(activation_map, pad_value=10, nrow=16)
plt.rcParams["figure.figsize"] = (8, 8)
plt.imshow(
np.transpose((img_grid.clamp(-1, 1) + 1) / 2, (1, 2, 0))
) # normalize to 0..1 range and change channel order for compability with numpy
plt.show()
handle = alexnet.features[10].register_forward_hook(module_hook)
Чтобы карта активаций была интерпретируема, надо использовать реальное изображение. Загрузим его:
!wget -q https://edunet.kea.su/repo/EduNet-web_dependencies/dev-2.0/L06/fox.jpg
from PIL import Image
img_fox = Image.open("fox.jpg")
plt.rcParams["figure.figsize"] = (8, 8)
plt.imshow(img_fox)
plt.axis("off")
plt.show()
Загрузим изображение, преобразуем в тензор и подадим на вход модели:
from torchvision import transforms
transform = transforms.Compose([transforms.Resize((256, 256)), transforms.ToTensor()])
tensor = transform(img_fox)
out = alexnet(tensor.unsqueeze(0))
torch.Size([256, 1, 15, 15])
Тут уже можно увидеть некоторые паттерны. Видно, что многие фильтры реагируют на лисицу.
Единственная опасная ловушка, которую можно легко заметить с помощью этой визуализации, заключается в том, что некоторые карты активации могут быть равны нулю для многих различных входов. Это может указывать на мертвые фильтры и может быть симптомом слишком высокой скорости обучения.
Отключим наш hook, чтобы он не мешал дальнейшим экспериментам
handle.remove()
Существуют техники, которые позволяют визуализировать паттерн, на который лучше всего активируется конкретный нейрон. Они основаны на подсчете градиента не по весам, а по входу (изображению) и его постепенной модификации.
Примеры:
Перейдем к картам активации предпоследнего слоя. В AlexNet предпоследний слой полносвязный, соответственно, активации — это вектор.
На вход сети мы подали изображение, закодированное при помощи $150528$ чисел ($224\times224\times3 = 150528$), а на выходе получили вектор из $4096$ чисел.
Фактически нейросеть понизила размерность наших данных (в $\approx36$ раз). При этом данные в векторе достаточно информативны, так как позволяют произвести классификацию на $1000$ классов.
Такие вектора признаков называются embedding и широко используются.
Последний слой
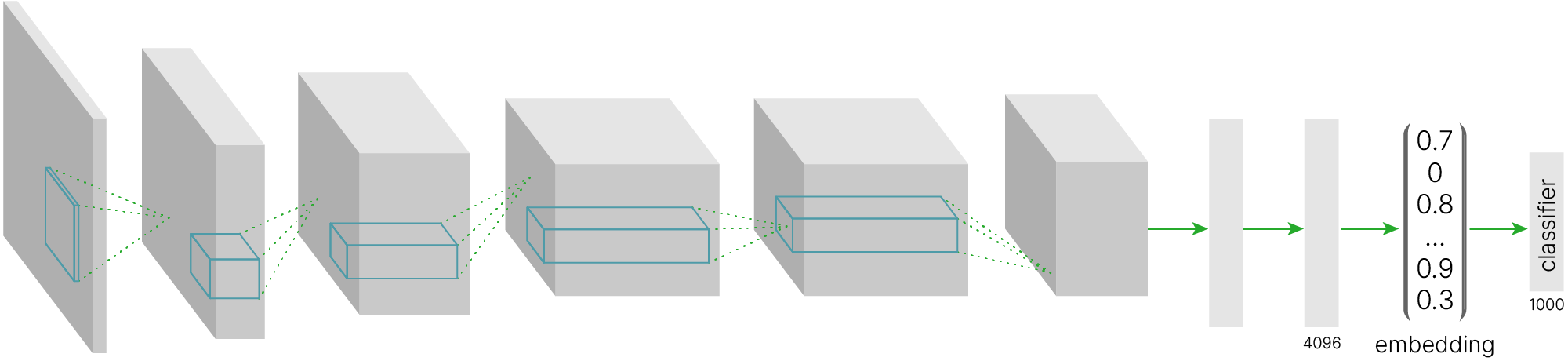
Чтобы убедиться в полезности полученных представлений, кластеризуем их при помощи k-nearest neighbors 📚[wiki] алгоритма.
Что бы получить embedding изображения, отключим последний слой. Выведем структуру модели, чтобы найти его:
print(alexnet)
AlexNet(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(11, 11), stride=(4, 4), padding=(2, 2))
(1): ReLU(inplace=True)
(2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(3): Conv2d(64, 192, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(4): ReLU(inplace=True)
(5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Conv2d(192, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(7): ReLU(inplace=True)
(8): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(9): ReLU(inplace=True)
(10): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): ReLU(inplace=True)
(12): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(avgpool): AdaptiveAvgPool2d(output_size=(6, 6))
(classifier): Sequential(
(0): Dropout(p=0.5, inplace=False)
(1): Linear(in_features=9216, out_features=4096, bias=True)
(2): ReLU(inplace=True)
(3): Dropout(p=0.5, inplace=False)
(4): Linear(in_features=4096, out_features=4096, bias=True)
(5): ReLU(inplace=True)
(6): Linear(in_features=4096, out_features=1000, bias=True)
)
)
И заменим его пустышкой nn.Identity() — класс, который возвращает вход без изменений:
alexnet.classifier[6] = nn.Identity()
Загрузим датасет:
from torchvision.datasets import CIFAR10
from torchvision.transforms import ToTensor, Resize, Normalize, Compose
from torch.utils.data import DataLoader, random_split
torch.manual_seed(42)
transform = Compose(
[Resize(224), ToTensor(), Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])]
)
testset = CIFAR10(root="./CIFAR10", train=False, download=True, transform=transform)
train, test, _ = random_split(testset, [512, 128, 10000 - 512 - 128])
train_loader = DataLoader(train, batch_size=128, shuffle=False, drop_last=True)
Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./CIFAR10/cifar-10-python.tar.gz
100%|██████████| 170498071/170498071 [00:06<00:00, 27056439.40it/s]
Extracting ./CIFAR10/cifar-10-python.tar.gz to ./CIFAR10
Добавим функцию, которая сохраняет выходы измененной модели в массиве, а также возвращает метки классов:
from tqdm import tqdm
def get_embeddings(loader):
embeddings = []
labels = []
for img, label in tqdm(loader):
emb = alexnet(img)
embeddings.append(emb.detach())
labels.append(label)
embeddings = torch.stack(embeddings).reshape(-1, 4096).numpy()
labels = torch.stack(labels).flatten().numpy()
return embeddings, labels
Превратим картинки в векторы признаков:
%%time
x, y = get_embeddings(train_loader)
100%|██████████| 4/4 [00:10<00:00, 2.64s/it]
CPU times: user 9.31 s, sys: 1.32 s, total: 10.6 s Wall time: 10.6 s
Теперь у нас есть $512$ векторов по $4096$ значения в каждом и $512$ меток классов:
print(x.shape, y.shape)
(512, 4096) (512,)
"Обучим" на них k-NN
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=5)
neigh.fit(x, y)
KNeighborsClassifier()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
KNeighborsClassifier()
Получим вектора-признаки (embeddings) для тестовых картинок
%%time
test_loader = DataLoader(test, batch_size=32, shuffle=False, drop_last=True)
test_emb, gt_labels = get_embeddings(test_loader)
100%|██████████| 4/4 [00:03<00:00, 1.26it/s]
CPU times: user 3.1 s, sys: 3.63 ms, total: 3.11 s Wall time: 3.17 s
Получаем предсказания и считаем accuracy:
from sklearn.metrics import accuracy_score
y_pred = neigh.predict(test_emb)
accuracy = accuracy_score(gt_labels, y_pred)
print("k-NN accuracy", accuracy)
k-NN accuracy 0.4609375
Как видим, активации на последних слоях сети достаточно информативны.
Как обучить нейросеть на своих данных, когда их мало?
Можно взять обученную модель, заменить у нее несколько последних слоев и обучить только их.
Ранее обученные слои будут извлекать признаки (feature extractor), и полученные таким образом представления (embedding) будут классифицироваться вновь добавленными слоями.
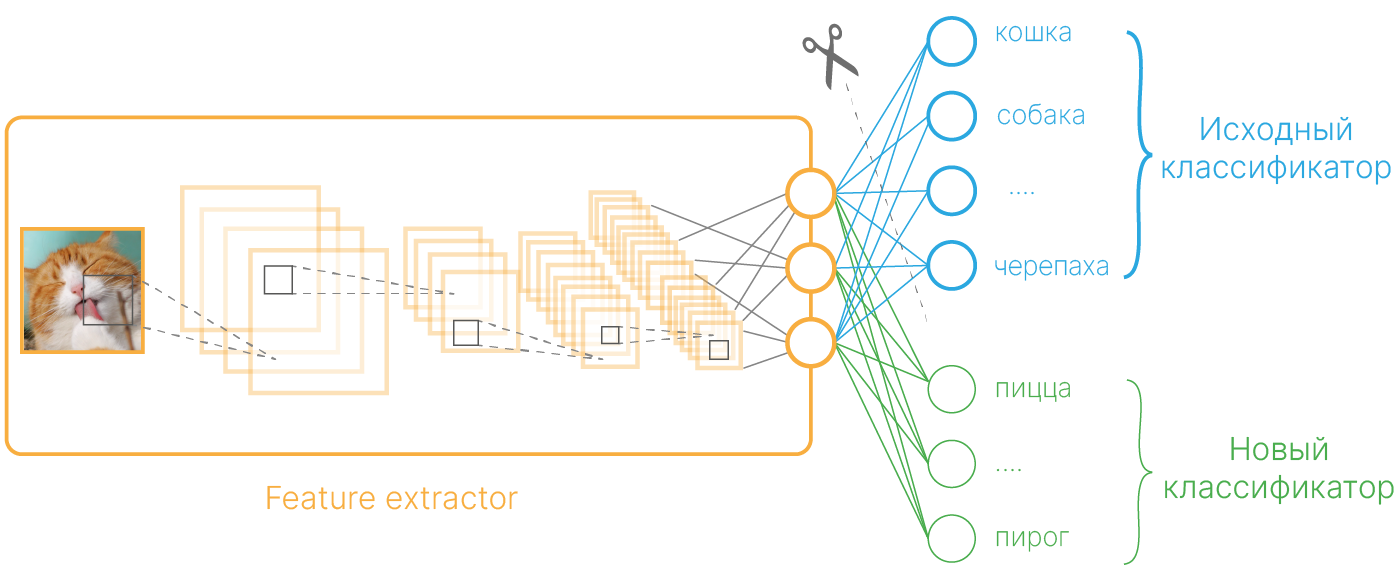
Возможно, что не все фильтры модели будут использованы эффективно на новой задаче. К примеру, если мы работаем с изображениями, связанными только с едой, не все фильтры на скрытых слоях предобученной на ImageNet модели окажутся полезны для нашей задачи.
Поэтому после того, как был обучен новый классификатор, можно дообучить все или некоторые промежуточные слои. При этом используют меньший learning rate, чем при обучении нейросети с нуля: мы знаем, что по крайней мере часть весов нейросети выполняет свою задачу хорошо, и не хотим испортить это быстрыми изменениями.
Поэтому такой подход называется fine-tuning — мы дополнительно "настраиваем" и промежуточные слои под нашу задачу.
Можно делать настройку постепенно: сначала учить только последние добавленные нами слои сети, затем самые близкие к ним, и после этого учить уже все веса нейросети вместе.
Иногда fine-tuning считается синонимом Transfer learning, в этом случае часть от предтренированной сети называют backbone ("позвоночник"), а добавленную часть — head ("голова").
Последовательно рассмотрим шаги, необходимые для реализации подхода transfer learning.
Первым шагом является выбор предварительно обученной модели, которую мы хотели бы использовать в качестве основы для обучения. Основным предположением является то, что признаки, которые умеет выделять из данных предобученная модель, хорошо подойдут для решения нашей частной задачи. Поэтому эффект от Transfer learning будет тем лучше, чем более схожими будут домены в нашей задаче и в задаче, на которой предварительно обучалась модель.
Для задач обработки изображений очень часто используются модели, предобученные на ImageNet. Такой подход распространен, однако если ваша задача связана, например, с обработкой снимков клеток под микроскопом, то модель, предобученная на более близком домене (тоже на снимках клеток, пусть и совсем других), может быть лучшим начальным решением.
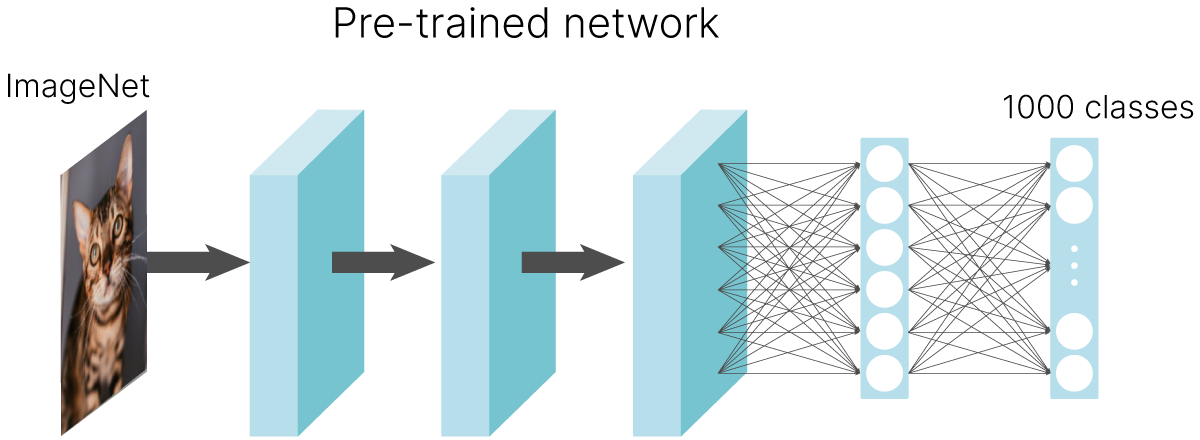
from torchvision import models
model = models.alexnet(weights="AlexNet_Weights.DEFAULT")
Мы предполагаем, что первые слои модели уже хорошо натренированы выделять важные признаки из данных, и мы не хотим их "сломать".
Если начнем дообучать их вместе с новыми слоями, которые инициализируются случайно, то на первых шагах обучения ошибка будет большой и мы можем сильно изменить "хорошие" предобученные веса.
Поэтому требуется "заморозить" предобученные веса. На практике заморозка означает отключение подсчета градиентов. Таким образом при последующем обучении параметры с отключенным подсчетом градиентов не будут обновляться.
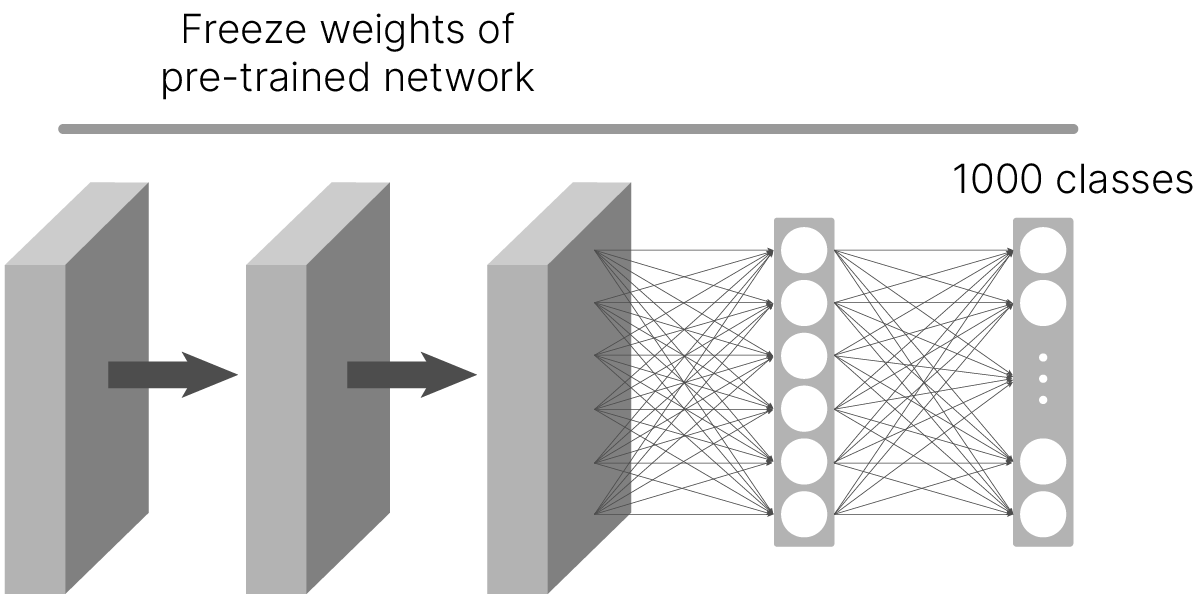
# Freeze model parameters
for param in model.parameters():
param.requires_grad = False
В отличие от начальных слоев, которые выделяют достаточно общие признаки из данных, более близкие к выходу слои предобученной модели сильно специфичны конкретно под ту задачу, на которую она обучалась. Для моделей, предобученных на ImageNet, последний слой заточен конкретно под предсказание 1000 классов из этого набора данных. Кроме этого, последние слои могут не подходить под новую задачу архитектурно: в новой задаче может быть меньше классов, 10 вместо 1000. Поэтому, требуется заменить последние один или несколько слоев предобученной модели на новые, подходящие под нашу задачу. При этом, естественно, веса в этих слоях будут инициализированы случайно. Именно эти слои мы и будем обучать на следующем шаге.
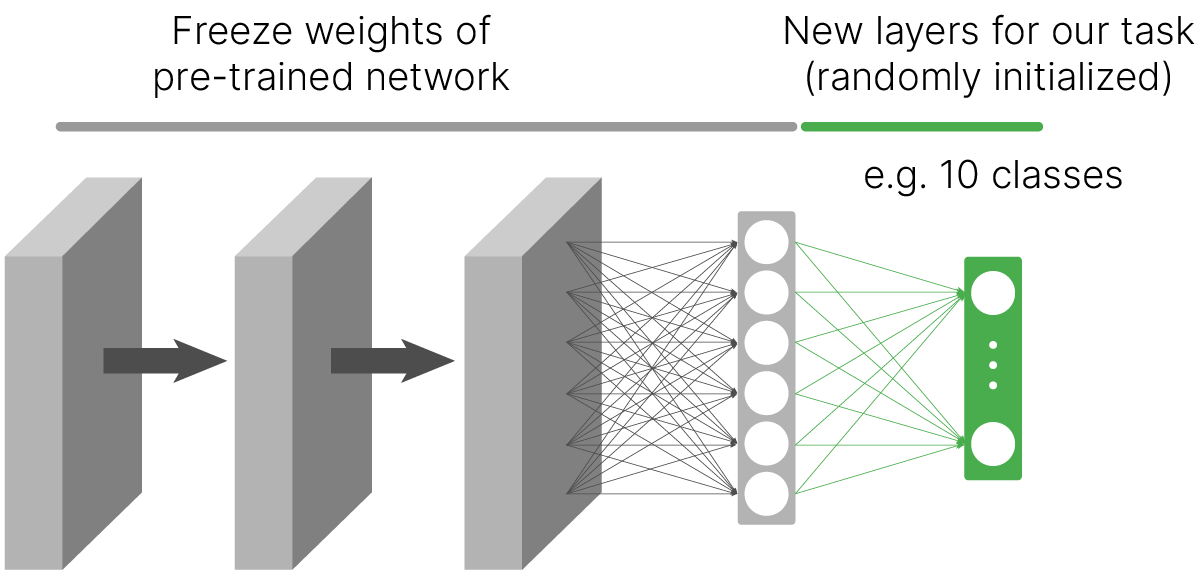
print(model.classifier)
Sequential( (0): Dropout(p=0.5, inplace=False) (1): Linear(in_features=9216, out_features=4096, bias=True) (2): ReLU(inplace=True) (3): Dropout(p=0.5, inplace=False) (4): Linear(in_features=4096, out_features=4096, bias=True) (5): ReLU(inplace=True) (6): Linear(in_features=4096, out_features=1000, bias=True) )
from torch import nn
model.classifier[6] = nn.Linear(4096, 10, bias=True) # For CIFAR
Убедимся, что обучаться будет только вновь добавленный слой:
for name, param in model.named_parameters():
print(name, "\t", param.requires_grad)
features.0.weight False features.0.bias False features.3.weight False features.3.bias False features.6.weight False features.6.bias False features.8.weight False features.8.bias False features.10.weight False features.10.bias False classifier.1.weight False classifier.1.bias False classifier.4.weight False classifier.4.bias False classifier.6.weight True classifier.6.bias True
Все, что нам теперь нужно — обучить новые слои на наших данных. При этом замороженные слои используются лишь как экстрактор высокоуровневых признаков. Обучение такой модели существенно ничем не отличается от обучения любой другой модели: используется обучающая и валидационная выборка, контролируется изменение функции потерь и функционала качества.
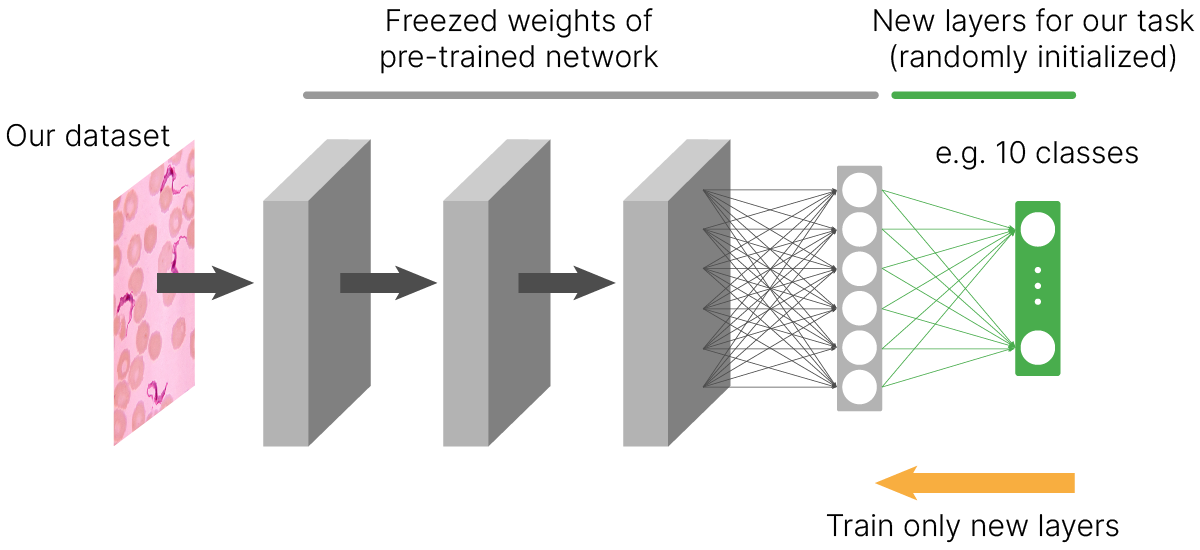
Загрузим датасет:
import torch
from torchvision.datasets import CIFAR10
from torchvision.transforms import ToTensor, Resize, Normalize, Compose
from torch.utils.data import DataLoader, random_split
torch.manual_seed(42)
transform = Compose(
[Resize(224), ToTensor(), Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])]
)
testset = CIFAR10(root="./CIFAR10", train=False, download=True, transform=transform)
train, test, _ = random_split(testset, [512, 128, 10000 - 512 - 128])
train_loader = DataLoader(train, batch_size=128, shuffle=False, drop_last=True)
Files already downloaded and verified
И напишем функцию для обучения:
from tqdm import tqdm
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
def train_model(model, num_epochs=1, lr=1e-3):
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), momentum=0.9, lr=lr)
for epoch in range(num_epochs):
for imgs, labels in tqdm(train_loader):
optimizer.zero_grad() # Clean existing gradients
outputs = model(imgs.to(device))
loss = criterion(outputs, labels.to(device))
loss.backward() # Backpropagate the gradients
optimizer.step()
print(f"\nEpoch {epoch} Loss {loss.item()}")
train_model(model, 5) # train only last layer
100%|██████████| 4/4 [00:01<00:00, 2.90it/s]
Epoch 0 Loss 2.304867744445801
100%|██████████| 4/4 [00:01<00:00, 3.67it/s]
Epoch 1 Loss 1.919417381286621
100%|██████████| 4/4 [00:01<00:00, 3.62it/s]
Epoch 2 Loss 1.4428484439849854
100%|██████████| 4/4 [00:01<00:00, 3.56it/s]
Epoch 3 Loss 1.1411782503128052
100%|██████████| 4/4 [00:01<00:00, 3.68it/s]
Epoch 4 Loss 0.9886724352836609
В модели могут быть слои, поведение которых различно при выводе (inference) и обучении. Например, слои Dropout и Batchnorm, которые будут обсуждаться на следующей лекции.
Если такие слои в модели есть, то их следует перевести в inference режим, используя метод nn.Module.eval()
После того, как мы обучили новые слои модели, и они уже как-то решают задачу, мы можем разморозить ранее замороженные веса, чтобы тонко настроить их под нашу задачу, в надежде, что это позволит еще немного повысить качество.
Нужно быть осторожным на этом этапе, использовать learning rate на порядок или два меньший, чем при основном обучении, и одновременно с этим следить за возникновением переобучения. Переобучение при fine-tuning может возникать из-за того, что мы резко увеличиваем количество настраиваемых параметров модели, но при этом наш датасет остается небольшим, и мощная модель может начать заучивать обучающие данные.
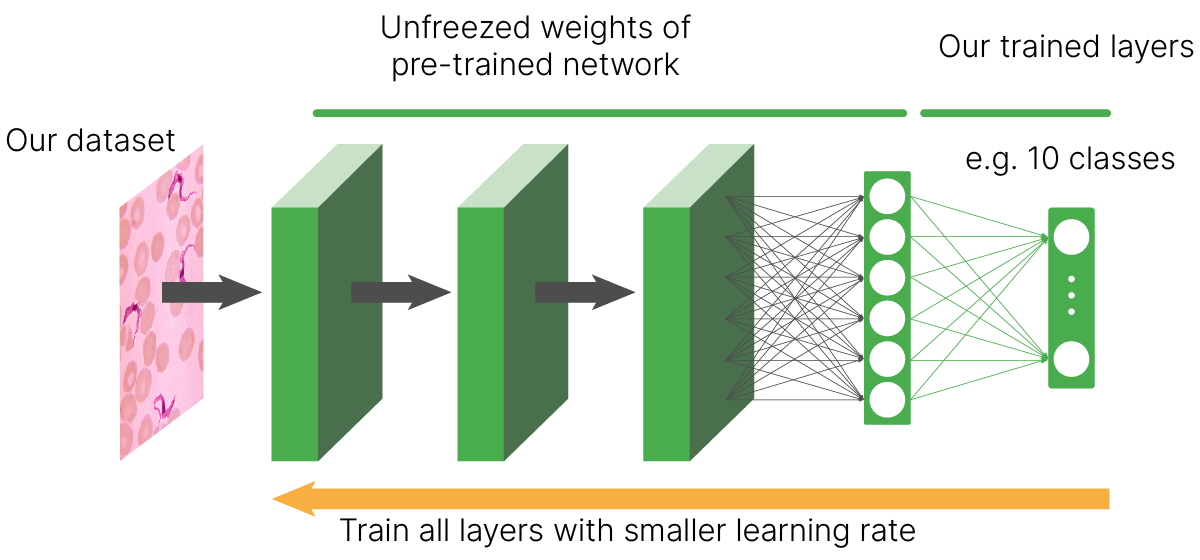
# Freeze model parameters
for param in model.parameters():
param.requires_grad = True
%%time
train_model(model, num_epochs=3, lr=1e-5) # fine tune all layers
100%|██████████| 4/4 [00:01<00:00, 3.02it/s]
Epoch 0 Loss 0.9192925095558167
100%|██████████| 4/4 [00:01<00:00, 3.16it/s]
Epoch 1 Loss 0.8809319138526917
100%|██████████| 4/4 [00:01<00:00, 3.08it/s]
Epoch 2 Loss 0.9289202690124512 CPU times: user 3.22 s, sys: 616 ms, total: 3.84 s Wall time: 4.07 s
Проверим accuracy:
test_loader = DataLoader(test, batch_size=32, shuffle=False, drop_last=True)
y_true = []
y_pred = []
for imgs, labels in test_loader:
outputs = model(imgs.to(device))
y_true.append(labels.numpy())
preds = outputs.argmax(dim=1)
y_pred.append(preds.detach().cpu().numpy())
import numpy as np
from sklearn.metrics import accuracy_score
y_true = np.stack(y_true).flatten()
y_pred = np.stack(y_pred).flatten()
accuracy = accuracy_score(y_true, y_pred)
print(f"Accuracy : {accuracy:.2f}")
Accuracy : 0.62
Точность на 512 не репрезентативна, но она уже выше, чем в получилась в домашнем задании.
Операция свертки инвариантна к сдвигу (не важно, где на изображении находится объект), но не к масштабированию и повороту.
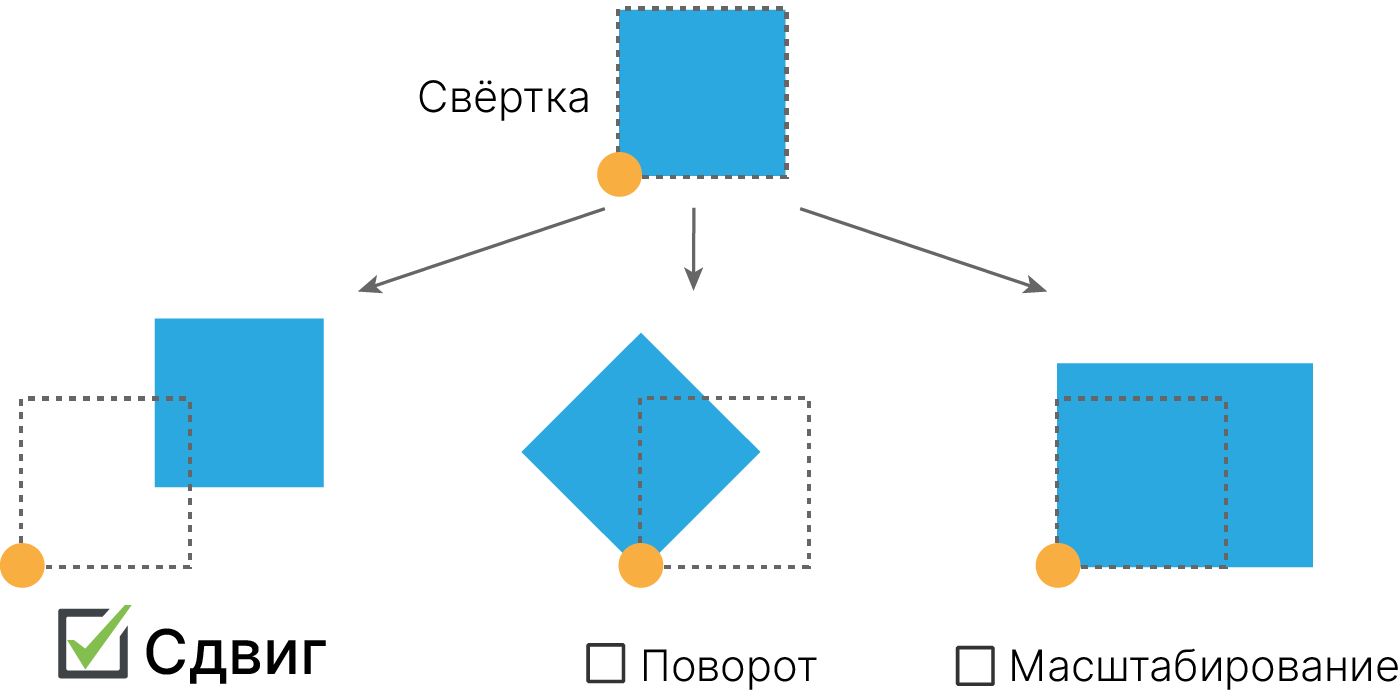
У этой проблемы нет красивого решения: если в обучающей выборке не было котов, висящих вверх лапами, то модель не будет их различать.
Нужно дополнить датасет такими изображениями, и самый простой способ это сделать — это преобразовать (отразить, повернуть, масштабировать и т.д.) уже имеющиеся.
Аугмента́ция (от лат. augmentatio — увеличение, расширение) — увеличение выборки обучающих данных через модификацию существующих данных.
Модели глубокого обучения обычно требуют большого количества данных для обучения. В целом, чем больше данных, тем лучше для обучения модели. В то же время получение огромных объемов данных сопряжено со своими проблемами (например, с нехваткой размеченных данных или с трудозатратами, сопряженными с разметкой).
Вместо того, чтобы тратить дни на сбор данных вручную, мы можем использовать методы аугментации для автоматической генерации новых примеров из уже имеющихся.
Помимо увеличения размеченных датасетов, многие методы self-supervised learning построены на использовании разных аугментаций одного и того же сэмпла.
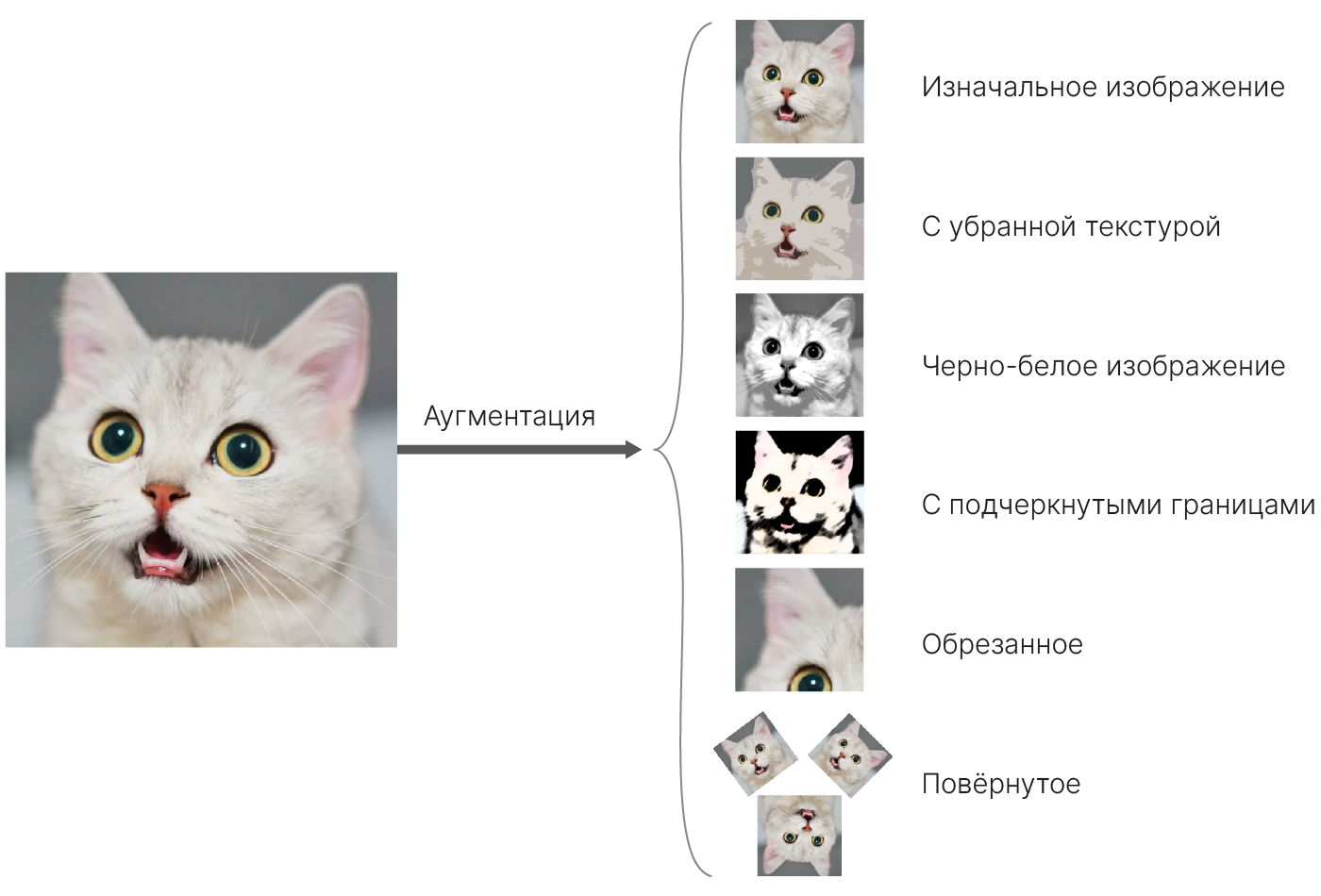
Важный момент: при обучении модели мы используем разбиение данных на train-val-test. Аугментации стоит применять только на train. Почему так? Конечная цель обучения нейросети — это применение на реальных данных, которые сеть не видела. Поэтому для адекватной оценки качества модели валидационные и тестовые данные изменять не нужно.
В любом случае, test должен быть отделен от данных еще до того, как они попали в DataLoader или нейросеть.
Другое дело, что аугментации на тесте можно использовать как метод ансамблирования в случае классификации. Можно взять sample → создать несколько его копий → по-разному их аугментировать → предсказать класс на каждой из этих аугментированных копий → выбрать наиболее вероятный класс голосованием (такой функционал реализован, например, в YOLO, о которой речь пойдет в следующих лекциях).
Инструментарий для аугментаций встроен в PyTorch 🛠️[doc]. Мы уже пользовались им, когда создавали датасет и передавали в конструктор параметр transform.
from torchvision.datasets import CIFAR10
from torchvision.transforms import ToTensor, Resize, Normalize, Compose
transform = Compose(
[Resize(224), ToTensor(), Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])]
)
testset = CIFAR10(root="./CIFAR10", train=False, download=True, transform=transform)
Files already downloaded and verified
Собствено, экземпляр объекта torchvision.transforms.Resize, созданный первым в списке (Resize(224)), и аугментирует изображение.
Отметим что аугментация происходит "на лету": аугментированное изображение не сохраняется на диск и сразу передается в модель.
Пакет torchvision.transforms 🛠️[doc] позволяет выполнить довольно много различных аугментаций. Посмотрим на некоторые из них.
Загрузим и отобразим пример картинки. Картинку отмасштабируем, чтобы она не занимала весь экран.
import torch
# setting random seed for reproducible illustrations
torch.manual_seed(42)
URL = (
"https://edunet.kea.su/repo/EduNet-web_dependencies/dev-2.0/L06/capybara_image.jpg"
)
!wget -q $URL -O test.jpg
from PIL import Image
from torchvision import transforms
from IPython.display import display
input_img = Image.open("/content/test.jpg")
input_img = transforms.Resize(size=300)(input_img)
display(input_img)
Рассмотрим несколько примеров аугментаций картинок. С полным списком можно ознакомиться на сайте документации torchvision 🛠️[doc].
Трансформация transforms.Random Rotation 🛠️[doc] принимает параметр degrees — диапазон углов, из которого выбирается случайный угол для поворота изображения.
Создадим переменную transform, в которую добавим нашу аугментацию, и применим ее к исходному изображению. Затем запустим следующую ячейку несколько раз подряд
import matplotlib.pyplot as plt
def plot_augmented_img(transform, input_img):
fig, ax = plt.subplots(1, 2, figsize=(15, 15))
augmented_img = transform(input_img)
ax[0].imshow(input_img)
ax[0].set_title("Original img")
ax[0].axis("off")
ax[1].imshow(augmented_img)
ax[1].set_title("Augmented img")
ax[1].axis("off")
plt.show()
transform = transforms.RandomRotation(degrees=(0, 180))
plot_augmented_img(transform, input_img)
transforms.GaussianBlur 🛠️[doc] размывает изображение с помощью фильтра Гаусса.
transform = transforms.GaussianBlur(kernel_size=(5, 9), sigma=(0.1, 5))
plot_augmented_img(transform, input_img)
transforms.RandomErasing 🛠️[doc] стирает на изображении произвольный прямоугольник. Она имеет параметр p — вероятность, с которой данная трансформация вообще применится к изображению.
Данная трансформация работает только с torch.Tensor, поэтому предварительно нужно применить трансформацию ToTensor, а затем ToPILImage, чтобы воспользоваться нашей функцией для отображения.
transform = transforms.Compose(
[transforms.ToTensor(), transforms.RandomErasing(p=1), transforms.ToPILImage()]
)
plot_augmented_img(transform, input_img)
Не лишним будет заметить, что некоторые трансформации могут существенно исказить изображение. Например, здесь, RandomErasing практически полностью стерла основной объект на снимке — капибару. Такая грубая аугментация может только навредить процессу обучения, и на практике нужно быть осторожным.
RandomErasing также имеет параметр scale — диапазон соотношения стираемой области к входному изображению. Попробуем уменьшить этот диапазон относительно значения по умолчанию, чтобы избежать нежелательного эффекта стирания капибары.
transform = transforms.Compose(
[
transforms.ToTensor(),
transforms.RandomErasing(p=1, scale=(0.02, 0.1)),
transforms.ToPILImage(),
]
)
plot_augmented_img(transform, input_img)
transform = transforms.ColorJitter(brightness=0.5, hue=0.3)
plot_augmented_img(transform, input_img)
Для этого будем использовать метод transforms.Compose 🛠️[doc], с которым мы хорошо знакомы. Нам нужно будет создать list со всеми аугментациями, которые будут применены последовательно.
transform = transforms.Compose(
[
transforms.GaussianBlur(kernel_size=(5, 9), sigma=(0.1, 5)),
transforms.RandomPerspective(distortion_scale=0.5, p=1.0),
transforms.ColorJitter(brightness=0.5, hue=0.3),
]
)
plot_augmented_img(transform, input_img)
Как видно, три аугментации, примененные последовательно, достаточно сильно изменили картинку. Разумнее применять не все сразу. Для этого есть соответствующие классы.
Для того, чтобы применять аугментации случайным образом, можно воспользоваться классом transforms.RandomApply 🛠️[doc], конструктор которого принимает на вход список аугментаций и вероятность p, с которой каждая аугментация будет применена.
transform = transforms.RandomApply(
transforms=[
transforms.GaussianBlur(kernel_size=(5, 9), sigma=(0.1, 5)),
transforms.RandomPerspective(distortion_scale=0.5),
transforms.ColorJitter(brightness=0.5, hue=0.3),
],
p=0.9,
)
plot_augmented_img(transform, input_img)
В других случаях может быть полезен класс transforms.RandomChoice 🛠️[doc], конструктор которого принимает на вход список аугментаций transforms, выбирает из него одну случайную аугментацию и применяет ее к изображению. Необязательным параметром является список вероятностей p, который указывает, с какой вероятностью каждая из аугментаций может быть выбрана из списка (по умолчанию каждая может быть выбрана равновероятно).
transform = transforms.RandomChoice(
transforms=[
transforms.GaussianBlur(kernel_size=(5, 9), sigma=(0.1, 5)),
transforms.RandomPerspective(distortion_scale=0.5, p=1.0),
transforms.ColorJitter(brightness=0.5, hue=0.3),
],
p=[0.2, 0.4, 0.6],
)
plot_augmented_img(transform, input_img)
plot_augmented_img(transform, input_img)
plot_augmented_img(transform, input_img)
Иногда может оказаться, что среди широкого спектра реализованных аугментаций нет такой, какую вы хотели бы применить к своим данным. В таком случае ее можно описать в виде класса и использовать наравне с реализованными в библиотеке.
Главное, что необходимо описать при создании класса — метод __call__. Он должен принимать изображение (оно может быть представлено в формате PIL.Image, np.array или torch.Tensor), делать с ним интересующие нас видоизменения и возвращать измененное изображение.
Рассмотрим пример добавления на изображение шума "соль и перец" 📚[wiki]. Наш метод аугментации будет и принимать на вход, и возвращать PIL.Image.
import numpy as np
from PIL import Image
class SaltAndPepperNoise:
"""
Add a "salt and pepper" noise to the PIL image
__call__ method returns PIL Image with noise
"""
def __init__(self, p=0.01):
self.p = p # noise level
def __call__(self, pil_image):
np_image = np.array(pil_image)
# create random mask for "salt" and "pepper" pixels
salt_ind = np.random.choice(
a=[True, False], size=np_image.shape[:2], p=[self.p, 1 - self.p]
)
pepper_ind = np.random.choice(
a=[True, False], size=np_image.shape[:2], p=[self.p, 1 - self.p]
)
# add "salt" and "pepper"
np_image[salt_ind] = 255
np_image[pepper_ind] = 0
return Image.fromarray(np_image)
transform = SaltAndPepperNoise(p=0.03)
plot_augmented_img(transform, input_img)
Dataset¶Возьмем папку с картинками.
# download files
!wget -q "https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/for_transforms.Compose.zip" -O data.zip
!unzip -qn "data.zip"
Напишем класс AugmentationDataset:
import glob
from torch.utils.data import Dataset
class AugmentationDataset(Dataset):
def __init__(self, root, transforms=None):
self.img_list = glob.glob(root + "*.jpg")
self.transforms = transforms
def __len__(self):
return len(self.img_list)
def __getitem__(self, i):
img = Image.open(self.img_list[i])
if self.transforms is not None:
img = self.transforms(img)
return img
Создадим list с аугментациями, которые мы хотим применить. Многие аугментации в PyTorch работают с Pillow Image, так что картинки не обязательно преобразовать в тензоры. transforms.ToTensor().
transform = transforms.Compose(
[
transforms.Resize((164, 164)),
transforms.GaussianBlur(kernel_size=(5, 9), sigma=(0.1, 5)),
transforms.RandomPerspective(distortion_scale=0.5),
# ToTensor()
]
)
augmentated_dataset = AugmentationDataset(
"/content/for_transforms.Compose/", transforms=transform
)
Отобразим аугментированные изображения:
plt.figure(figsize=(22, 2))
for i, img in enumerate(augmentated_dataset):
plt.subplot(1, len(augmentated_dataset) + 1, 1 + i)
plt.axis("off")
plt.imshow(np.array(img))
plt.show()
Кроме методов, реализованных в PyTorch, существуют и специализированные библиотеки для аугментации изображений, в которых реализованы дополнительные возможности (например, наложение теней, бликов или пятен воды на изображение).
Например:
Важно: при выборе методов аугментации имеет смысл использовать только те, которые будут в реальной жизни.
Например, нет смысла:
При обучении моделей в PyTorch нам часто приходиться переписывать цикл обучения (train loop). Это дублирование кода, которое нарушает принцип DRY 📚[wiki].
Кроме того, нам нужно следить за процессом обучения модели. Например если loss "взрывается" или выходит на плато, как правило есть смысл остановить обучение. Чтобы контролировать этот процесс, приходится добавлять дополнительный код для вывода и/или логирования метрик.
При проведении реальных экспериментов логирование результатов станет необходимым. В задании вам предстоит научиться работать с фреймворком Lightning 🐾[git], который облегчает написание train loop и облегчает логирование результатов.
Дополнительные материалы:
stride = 2.debug_train, debug_val, _ = random_split(dataset, [5000, 1000, 54000])Литература
Введение в сверточные нейронные сети:
Сверточный слой нейросети:
Применение свёрточных слоёв:
Другие виды сверток:
Визуализация:
Lightning:
Дополнительно: