Классическое машинное обучение
Помимо нейронных сетей, обучение работе с которыми является основной задачей курса, есть и другие подходы к проблеме создания систем, помогающих решать те или иные задачи.
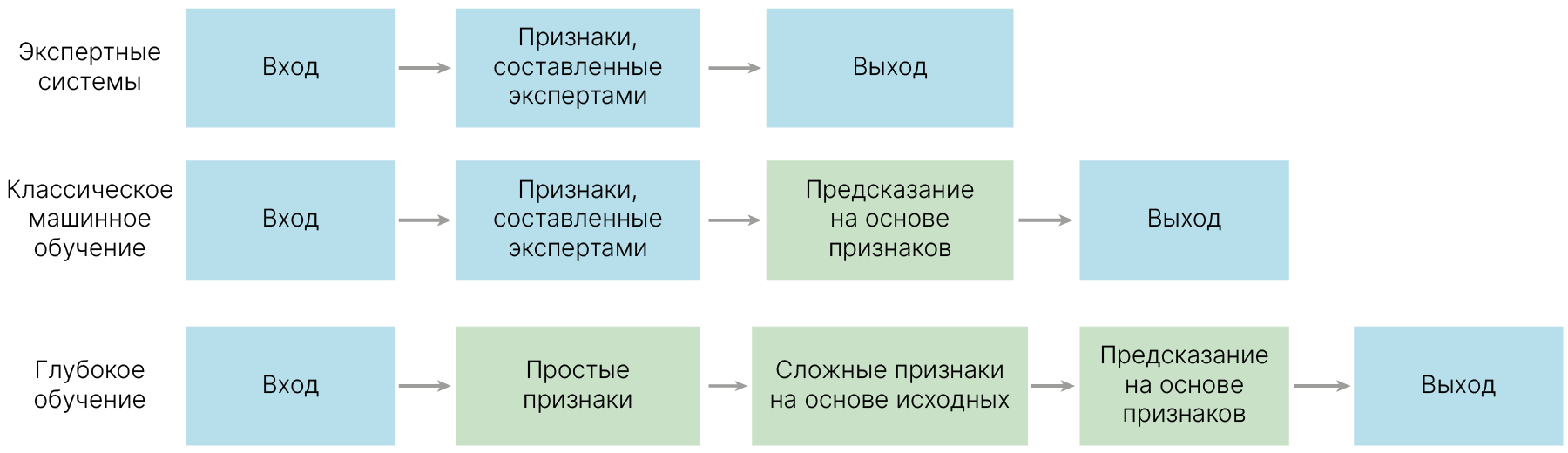
Самым первым подходом к созданию системы, способной на основе входных данных делать какие-то выводы, были так называемые Rule-based systems. В этих системах и за описание объекта — выделение значимых признаков, и за выработку правил, по которым система должна принимать то или иное решение, отвечал человек.
Такие системы до сих пор используются, например, в определителях растений. Определители представляют собой набор утверждений, например: "Растение имеет стержневую корневую систему", "Плод растения — костянка", на основе согласия/несогласия с которыми книга отсылает вас к другим утверждениям или, в конце концов, к названию растения.
Результативность такого подхода зависит от:
Единственной выгодой такой системы по сравнению с экспертом является то, что в большинстве случаев требования к умениям пользователя все же меньше.
Игрушечный пример такой схемы:
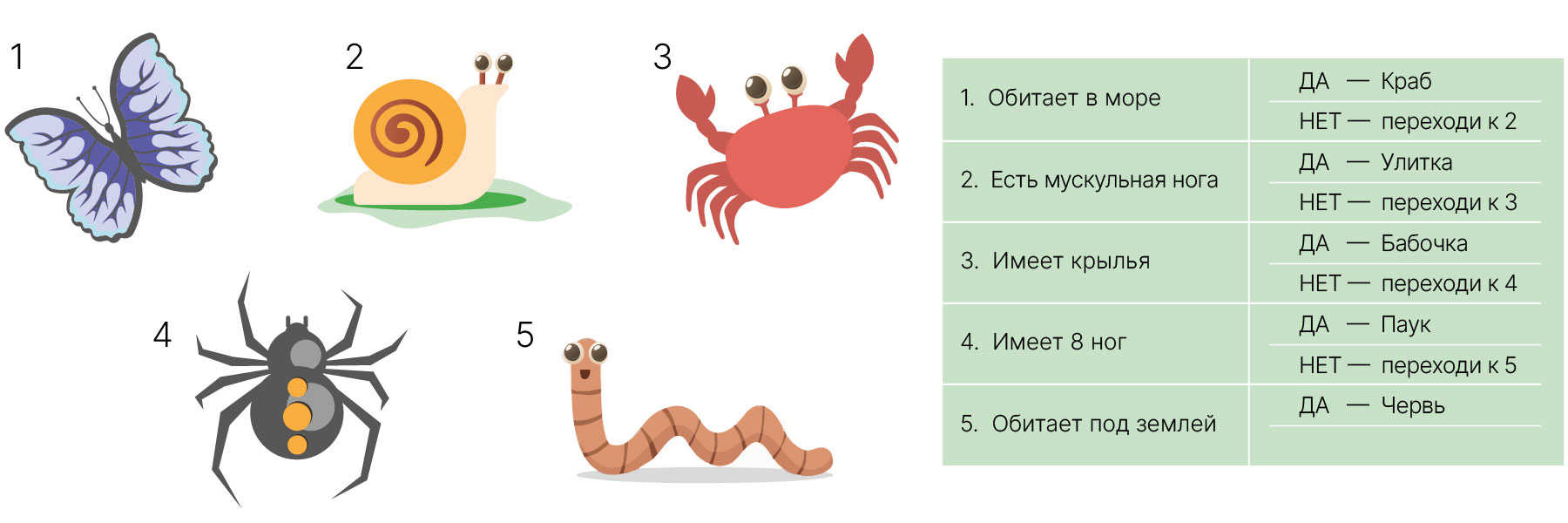
Классическое машинное обучение избавляет нас от необходимости вручную составлять какие-то правила.

В этом подходе от нас все равно требуется описание нашего объекта определенными признаками — мы должны получать это описание либо вручную, либо обрабатывая объект какими-то программами. Чтобы отличать такие признаки от признаков, которые автоматически выделяют нейронные сети, их называют hand-designed features.
Затем эти описанные объекты передаются алгоритму, который уже сам формирует набор правил, по которому он должен решать поставленную задачу. Уже разобранные вами линейная регрессия и SVM сами выбирают, какие признаки и с какими весами им учитывать при принятии финального решения. В некоторых случаях (например, SVM) признаки могут дополнительно (явно или неявно) преобразовываться внутри самой модели, и на их основе могут формироваться новые признаки.
Но главное ограничение всегда остается: за описание объекта отвечает какой-то внешний источник и то, какие признаки подавать алгоритму на вход, решает человек. А набор возможных преобразований признаков, как правило, строго фиксирован.
И составление таких признаков требует от исследователя очень хорошего знания изучаемой темы, знания специфики работы используемого алгоритма — к примеру, подавать алгоритму на вход попарные произведения всех признаков, или алгоритм сам в ходе работы их явно или неявно получит.
В глубоком обучении признаки может выделить нейросеть. Важно понимать, что нейросеть не гарантирует нахождение качественных признаков, но имеет шансы их получить.

Нейросеть преобразует признаковое пространство от слоя к слою и сама определяет, какие признаки для данных объектов и для данной задачи важны, и итеративно выделяет сначала простые признаки, а затем комбинирует их в более сложные. В то время как качество подходов классического машинного обучения по мере увеличения размера обучающей выборки со временем выходит на плато, для нейросетей это плато наступает сильно позже или вообще не наступает.
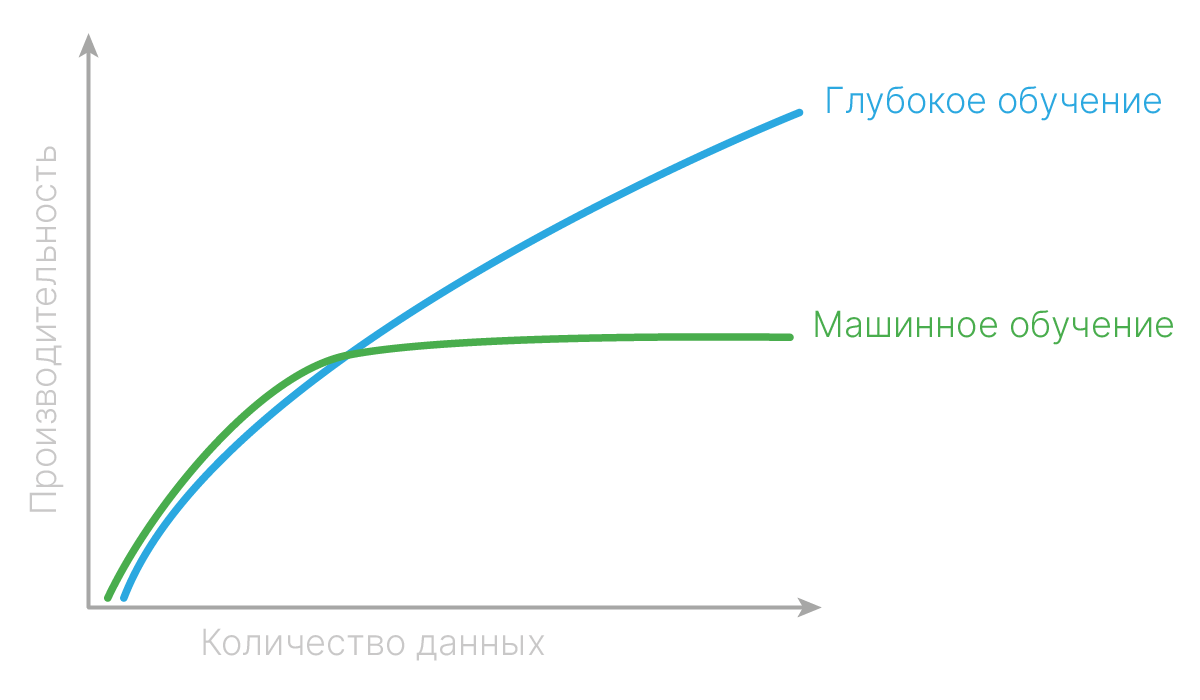
Потенциально такой подход позволяет почти не применять человеческую экспертизу при построении модели под задачу. Однако в реальности человеческая экспертиза теперь переходит на уровень подбора архитектуры нейросети.
Существует ряд причин, почему важно знать и применять методы классического машинного обучения:
Деревья решений — это одни из первых моделей машинного обучения, которые были известны человеку. Изначально их строили без специальных алгоритмов, а просто вручную.
Когда требовалось принять решение по проблеме, для которой построено дерево, человек брал и проходился по этому дереву.
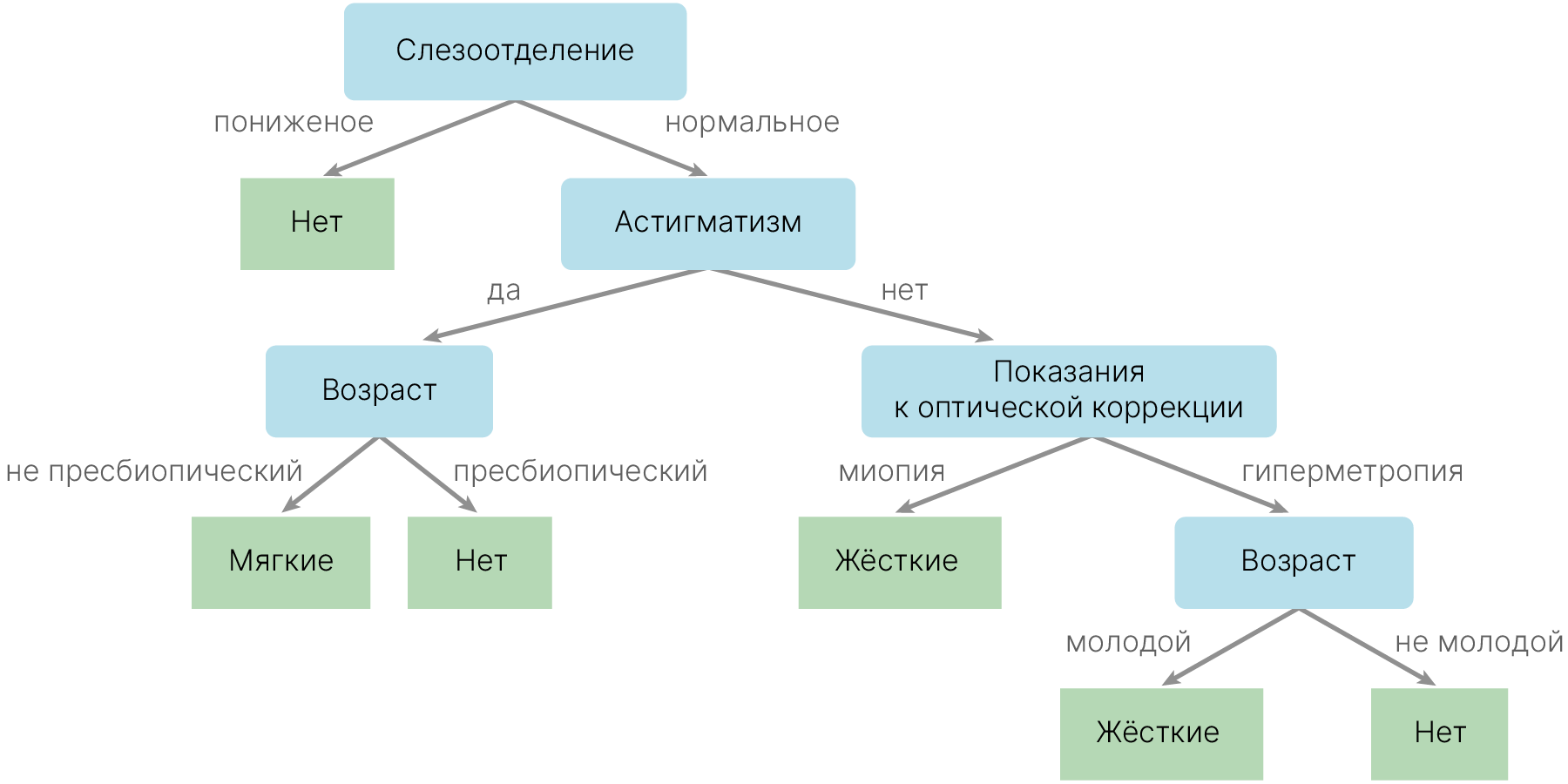
За принципом работы дерева решений стоит понятная интуиция. В каждом узле есть какой-то вопрос. Например, нормальное ли у человека слезоотделение, есть ли у него астигматизм и так далее. И, отвечая на каждый из этих вопросов, мы перемещаемся по дереву до тех пор, пока не придем к нужному типу линз.
Такое дерево решений можно построить без использования моделей машинного обучения, просто на основании опыта многих врачей (экспертные системы).
Вручную такие деревья строить тяжело, для большого объема данных их руками и не построишь. Также возникает вопрос: зачем нужна такая старая модель?
Оказывается, что эти модели могут быть неожиданно эффективны и их можно автоматически строить с помощью алгоритмов и делать это достаточно быстро даже на больших объемах данных.

По словам Энтони Голдблума, основателя и генерального директора Kaggle, на соревнованиях побеждают алгоритмы, основанные на деревьях решений, и нейронные сети.
Где побеждают ансамбли деревьев решений?
В любой задаче, где нет какой-то локальной связанности, которая есть в изображениях, текстах и т.д., деревья решений эффективнее, чем нейронные сети.

Принцип работы дерева решений можно проиллюстрировать на данном примере. Есть 2 признака, в данном случае вещественных. Для каждой точки мы создаем вопрос: признак $x_1$ больше $0.7$ или меньше? Если больше $0.7$, то это красная точка. Если меньше $0.7$, то идем во второй внутренний узел T2 и спрашиваем: признак $x_2$ меньше $0.5$ или больше? Если меньше $0.5$, то точка будет красная, в другом случае — синяя.
Разбиение пространства
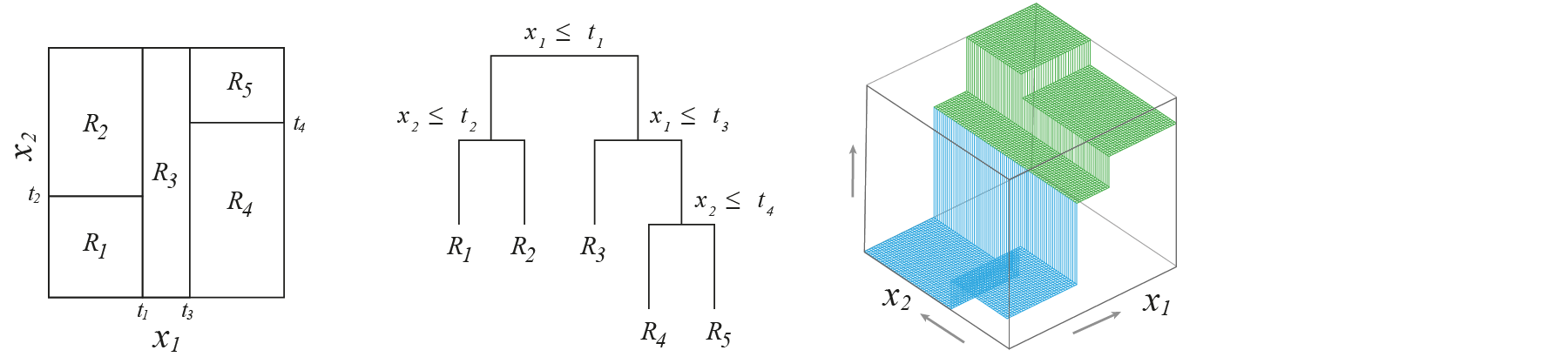
Дерево решений делит пространство признаков с помощью плоскостей на области, и в каждой из этих областей предсказывается константная величина.
Деревья решений, как правило, используются при решении 2-х типов задач — классификации и регрессии. Первая — классификация. Например, предсказание типа линз.

Особенно актуальны модели, которые могут предсказывать вероятности классов. Жесткие предсказания — не самый удачный вариант, лучше оставить человеку возможность выбирать. К примеру, лекарства всегда действуют с какой-то вероятностью, потому что невозможно учесть все факторы.
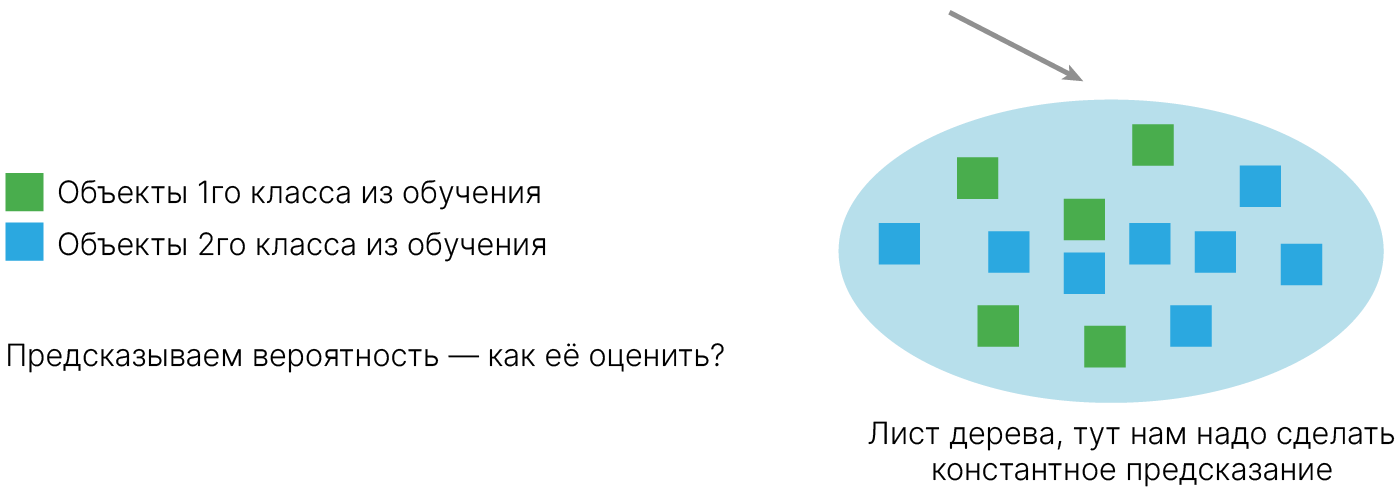
В деревьях решений в каждом листе находятся разные объекты, то есть каждому листу могут соответствовать объекты разных классов, а предсказать нужно один.
Мы хотим оценить вероятность принадлежности объекта к какому то определенному классу. Как это сделать: число представителей данного класса делим на общее число объектов. Это дает нам одну важную интуицию: желательно, чтобы в листе дерева было не очень мало объектов. Чем объектов меньше, тем больше возможная ошибка.
Это согласуется с тем, как мы делаем в статистике. При построении дерева мы видим только обучающую выборку, а хотим делать выводы о генеральной совокупности. Конкретно здесь мы оцениваем, какая доля из объектов, попадающих в данный узел, принадлежит нужному классу. Можно использовать распределение Бернулли 📚[wiki] для двух классов или мультиномиальное распределение 📚[wiki] для большего количества классов.
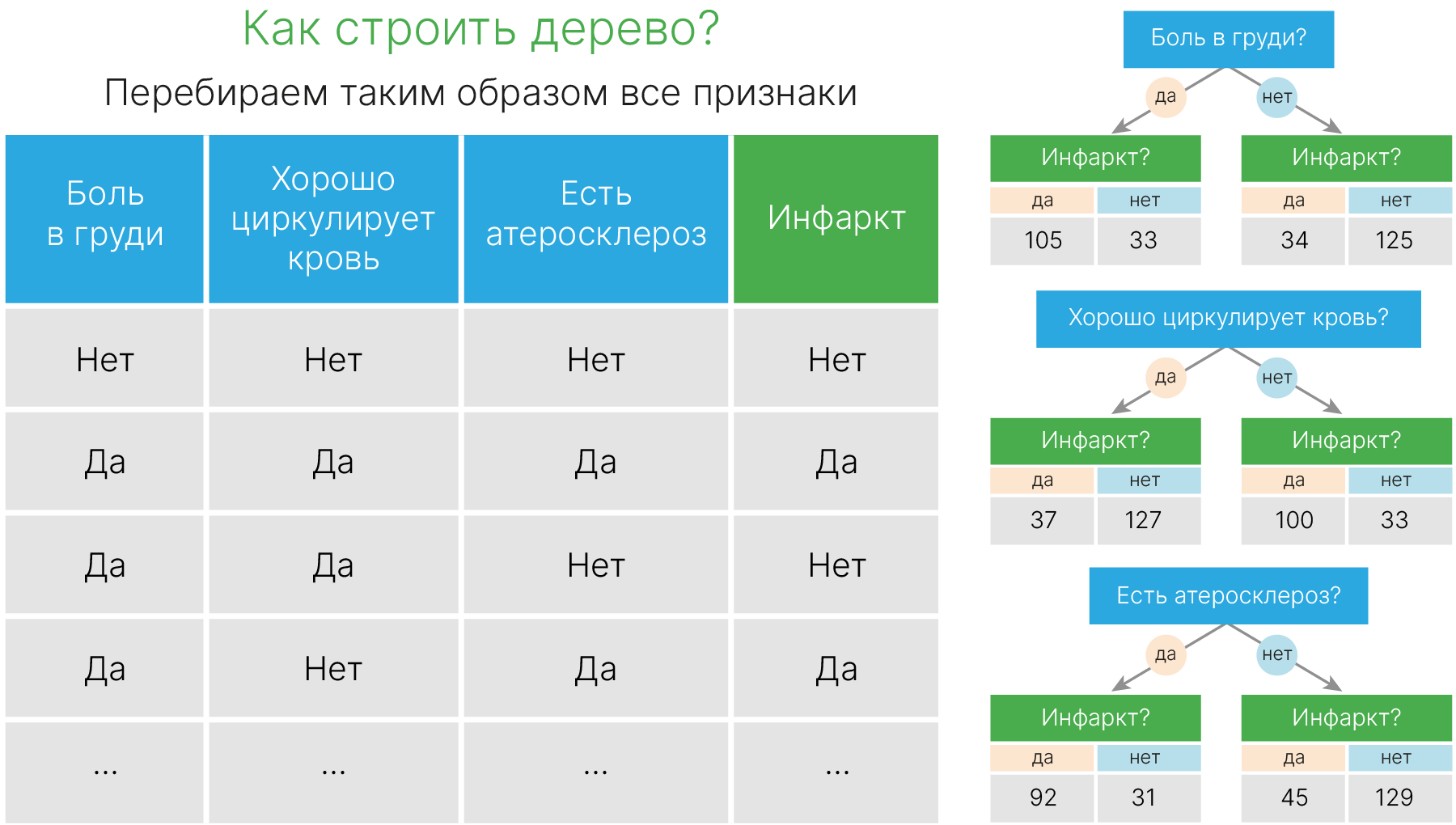
Представим, что мы решаем задачу бинарной классификации (есть инфаркт у человека или нет). В наших табличных данных только бинарные признаки. Мы хотим построить дерево решений по этой таблице.
Возьмем в качестве первого вопроса признак "боль в груди". В 1-ом и во 2-ом листе получается разное распределение людей. В левом листе инфаркт более вероятен, в правом — менее вероятен.
Другим признаком может быть “как хорошо циркулирует кровь”, в таком случае тоже получится неплохое разделение. Последний признак — “есть ли атеросклероз”.
Мы получили три разбиения по разным признакам. Теперь мы бы хотели выбрать лучший признак, а для этого нам нужно их сравнить.
Логично выбрать такое разбиение, которое дает нам "хорошие" узлы — те, в которых преимущественно сосредоточены объекты одного класса
Одна из используемых метрик называется Gini ✏️[blog] . Она считается по следующей формуле:
$$\large \text{Gini} = 1 - \sum_ip_i^2$$Gini — мера неопределенности ✏️[blog] значения класса внутри узла. Соответственно, чем она ниже, тем лучше получившийся узел.
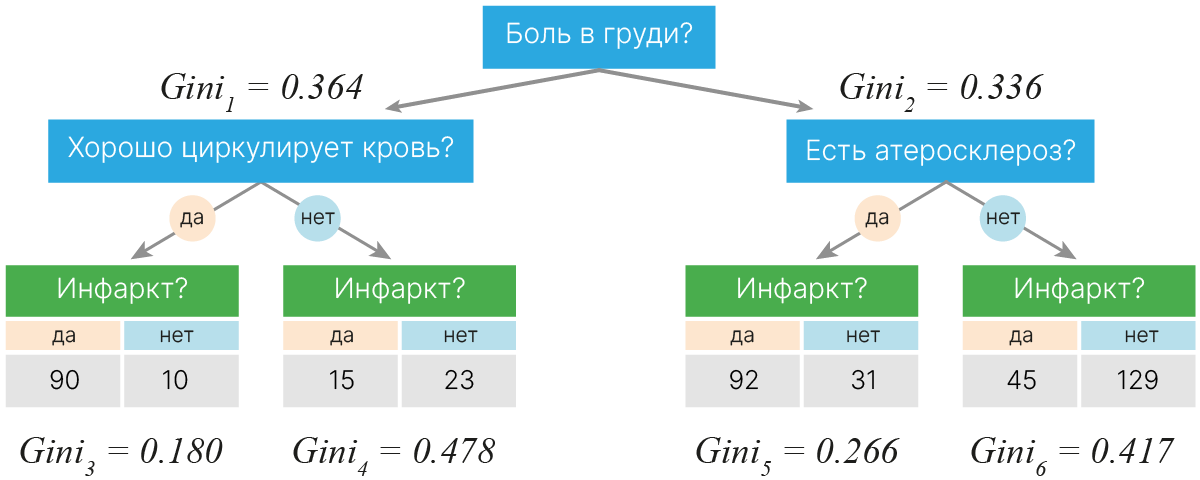
Посчитаем Gini для признака "Боль в груди":
$\text{Gini}_1 = 1- (\dfrac{105}{105+33})^2 - (\dfrac{33}{105+33})^2 = 0.364$
$\text{Gini}_2 = 1- (\dfrac{34}{34+125})^2 - (\dfrac{125}{34+125})^2 = 0.336$

Такую метрику можно посчитать для каждого узла. Дальше посчитать метрику для следующего узла. Дальше можем оценить насколько стал лучше результат в зависимости от используемого признака.
где $n_1, n_2$ — число объектов в листьях,
$ \quad\ \text{Gini}_0$ — чистота исходного узла.
Боль в груди:
$\text{Impurity decrease} = 0.498 - (\dfrac{138}{138+159})\cdot 0.364 - (\dfrac{159}{138+159})\cdot 0.336 = 0.149$
Хорошо циркулирует кровь:
$\text{Impurity decrease} = 0.498 - (\dfrac{164}{164+133})\cdot 0.349 - (\dfrac{133}{164+133})\cdot 0.373 = 0.138$
Есть атеросклероз:
$\text{Impurity decrease} = 0.498 - (\dfrac{123}{123+174})\cdot 0.377 - (\dfrac{174}{123+174})\cdot 0.383 = 0.117$

Выбираем это разбиение как приводящее к наибольшему уменьшению Impurity
Наибольший $\text{Impurity decrease}$ в признаке “боль в груди”. Значит, мы возьмем “боль в груди” как признак, на основании которого продолжим строить дерево.
Каждый раз мы будем выбирать новые признаки. В одном листе один признак лучше разделяет его на 2, в другом — другой. Тут мы остановились при достижении глубины дерева 2.
Мы могли выбрать другой критерий остановки. Например, когда у нас получатся листья, в которых есть объекты только 1 класса. В этом случае не имеет смысла использовать другие разбиения. Либо может сложиться ситуация, когда разбиение по признаку, которое мы дополнительно взяли, ситуацию никак не улучшает.
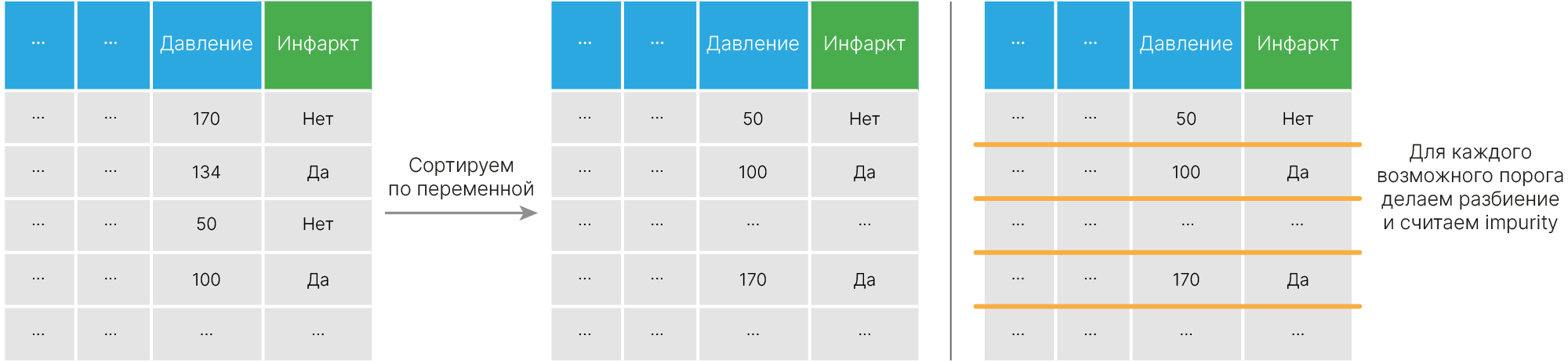
Вещественный признак сортируется, после чего мы выбираем оптимальный порог для разбиения. Для этого считаем impurity_decrease для каждого порога и выбираем лучший.
Для решения задач регрессии дерево строится практически так же, но есть несколько нюансов.

Как лучше всего одним числом охарактеризовать все эти объекты, попавшие в один лист?

Если мы вспомним статистику, то у нас нет однозначного ответа. Мы можем для распределения всех этих объектов в листе предсказывать наиболее частое значение, медиану, среднее значение.
Обычно предсказывают среднее значение, потому что с ним легче всего работать и его чаще всего используют в статистике.
Хотим оценить среднее всех объектов генеральной совокупности, попадающих в данный узел, используя объекты из тренировочной выборки, попавшие в данный узел.
$$\large \overline{y} = \dfrac {\sum_i y_i} {n}$$У нашей оценки будет дисперсия, которая показывает, насколько сильно мы можем ошибаться по сравнению с реальным (несмещенным) средним.
$$\large D(Y) = \dfrac {\sum_{i=1}^n(y_i-\overline{y})} {n-1} $$Из-за неточности в оценке среднего при оценке дисперсии в знаменателе стоит $n-1$. Желательно иметь в каждом листе достаточное число объектов, чтобы компенсировать эту $-1$.
Теперь надо сформулировать критерий качества узла для регрессионного дерева. Мы хотим, чтобы значения в узле отличались как можно меньше. В этом случае наше среднее будет предсказывать значение для объекта, попавшего в узел, с меньшей ошибкой. В идеале мы хотим, чтобы все значения были одинаковы.
MSE на тренировочной выборке, если мы предсказываем ее среднее, будет таким:
$$\large \text{MSE} = \frac 1 N \sum_{l=1}^L \sum_{i=1}^{n_l} (y_{li} - \overline{y_l})^2 = \frac 1 N \sum_{l=1}^L \sum_{i=1}^{n_l}\dfrac{n_l-1}{n_l}D(Y_l),$$где $N$ — общее количество объектов в выборке, $L$ — общее число листьев, $n_l$ — число объектов в листе $l$.
Уменьшение дисперсии листьев $D(Y_l)$ приводит к уменьшению $MSE$.
Дополнительно будем взвешивать дисперсии на размер узла. Иначе самыми выгодными будут разбиения, отправляющие в один из узлов только один объект.
Разбиение регрессионного дерева:
$$\large R_1(j, s) = \{ Y | x_j \leq s \} \ \text{and} \ R_2(j, s) = \{ Y | x_j > s \}$$Мера качества узла — дисперсия оценки $R_0$.
Остальное так же, как с классификацией:
$$\large \frac{D_{R_1} \cdot n_1 + D_{R_2} \cdot n_2}{n_1 + n_2} < D_{R_0} $$Взгляд с точки зрения функционального анализа
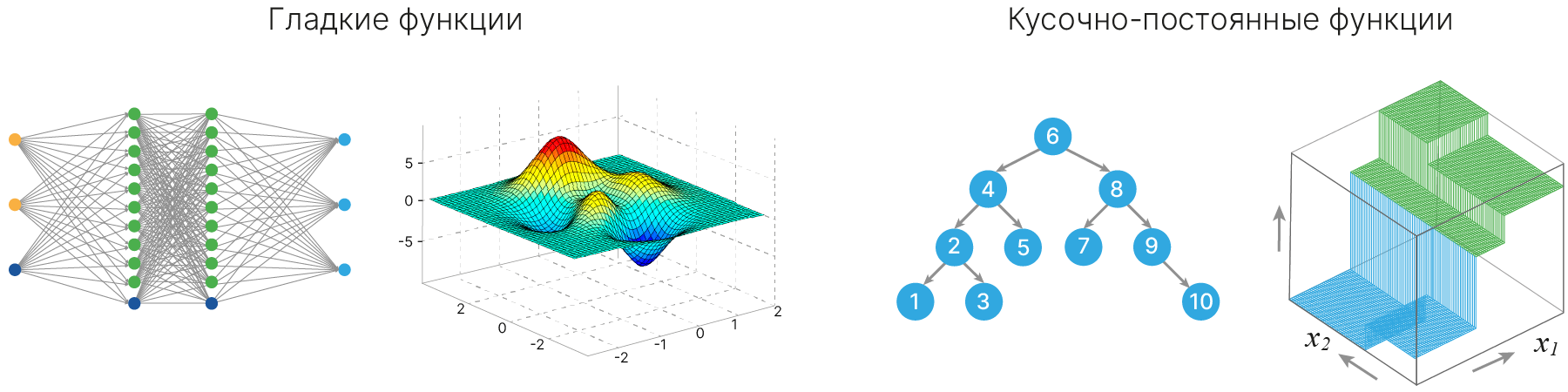
$\displaystyle \qquad \qquad h(x) = \sum \sigma(\dots \sum(w^Tx)) \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad h(x) = \sum_dc_dI\{x \in R_d\}$
У деревьев решений есть еще одно хорошее свойство. Позже вы познакомитесь с замечательной теоремой об универсальном аппроксиматоре 📚[wiki]. Ее суть в том, что нейросеть с одним скрытым слоем сможет аппроксимировать любую заданную гладкую функцию.
Для деревьев решений есть аналогичная теорема, говорящая о том, что дерево может аппроксимировать любую заданную кусочно-постоянную функцию.
Дерево решений, в отличие от нейронной сети, может адаптироваться к выборке любого размера, любому количеству признаков. Для нейронной сети эта теорема предполагает, что можно бесконечно увеличивать скрытые слои.
В случае же с деревьями решений лист разбивается еще на 2 части. Это можно делать бесконечно до тех пор, пока в каждом листе не окажется по одному объекту. Это приведет к сильному переобучению, но, если бы у нас была вся генеральная совокупность, мы бы выучили ее гораздо легче деревом решений, чем нейронной сетью.

Деревья решений не используются в чистом виде, потому что они неустойчивы. Если у нас есть данные, и мы удалим из них 2 объекта, то дерево решений может сильно поменяться.
Продемонстрируем неустойчивость решения, получаемого при помощи деревьев решений, на примере датасета Iris (ирисы Фишера 📚[wiki]).
Ирисы Фишера состоят из данных о 150 экземплярах ириса, по 50 экземпляров трёх видов: Ирис щетинистый (Iris setosa), Ирис виргинский (Iris virginica) и Ирис разноцветный (Iris versicolor).
Для каждого экземпляра измерялись четыре характеристики (в сантиметрах):
Будем учиться отделять Ирис виргинский (versicolor) от остальных видов.
from sklearn.datasets import load_iris
import pandas as pd
dataset = load_iris()
df = pd.DataFrame(dataset.data, columns=dataset.feature_names)
df["target"] = dataset.target != 1 # 0 for setosa, 1 - versicolor, 2 - virginica
Сделаем два разных разбиения на обучение и тест. И посмотрим, будут ли отличаться деревья, построенные для данных разбиений.
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
# first set of points
x_train1, x_test1, y_train1, y_test1 = train_test_split(
df[dataset.feature_names], df["target"], random_state=0
)
clf1 = DecisionTreeClassifier(max_depth=3)
clf1.fit(x_train1, y_train1)
# second set of points
x_train2, x_test2, y_train2, y_test2 = train_test_split(
df[dataset.feature_names], df["target"], random_state=42
)
clf2 = DecisionTreeClassifier(max_depth=3)
clf2.fit(x_train2, y_train2)
fn = ["sepal length (cm)", "sepal width (cm)", "petal length (cm)", "petal width (cm)"]
cn = ["setosa", "versicolor", "virginica"]
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5), dpi=100)
tree.plot_tree(clf1, feature_names=fn, class_names=cn, filled=True, ax=axes[0])
tree.plot_tree(clf2, feature_names=fn, class_names=cn, filled=True, ax=axes[1])
plt.show()
Видим, что даже деревья максимальной глубины 3 уже не совпадают между собой. Справедливо отметить, что у нас маленький датасет — как правило, чем датасет больше, тем устойчивее будет получаться дерево на первых уровнях.
Если использовать деревья бОльшей глубины, то и структура деревьев (то, как они выглядят, даже если не обращать внимания на конкретные признаки в узлах), будет отличаться.
# first set of points
clf1 = DecisionTreeClassifier(max_depth=10, random_state=0)
clf1.fit(x_train1, y_train1)
# second set of points
clf2 = DecisionTreeClassifier(max_depth=10, random_state=42)
clf2.fit(x_train2, y_train2)
fn = ["sepal length (cm)", "sepal width (cm)", "petal length (cm)", "petal width (cm)"]
cn = ["setosa", "versicolor", "virginica"]
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5), dpi=100)
tree.plot_tree(clf1, feature_names=fn, class_names=cn, filled=True, ax=axes[0])
tree.plot_tree(clf2, feature_names=fn, class_names=cn, filled=True, ax=axes[1])
plt.show()
Если алгоритм при небольшом изменении признаков сильно меняет свое решение, то это указывает на возможное переобучение. Алгоритм сильно реагирует на любой шум в данных— доверять его решениям опасно.
Посмотрим это на синтетическом датасете:
# handson-ml
import numpy as np
from matplotlib.colors import ListedColormap
def plot_decision_boundary(
clf, x, y, axes=[-1.5, 2.5, -1, 1.5], alpha=0.85, contour=True, bolded=False
):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
x_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(x_new).reshape(x1.shape)
custom_cmap = ListedColormap(["#FEE7D0", "#bea6ff", "#B8E1EC"])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
if contour:
custom_cmap2 = ListedColormap(["#FEE7D0", "#5D5DA6", "#B8E1EC"])
if bolded:
custom_cmap2 = ListedColormap(["#FEE7D0", "#5D5DA6", "#000000"])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2)
plt.plot(x[:, 0][y == 0], x[:, 1][y == 0], "D", c="#F9B041", alpha=alpha)
plt.plot(x[:, 0][y == 1], x[:, 1][y == 1], "o", c="#2DA9E1", alpha=alpha)
plt.axis(axes)
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
import sklearn
x, y = sklearn.datasets.make_moons(n_samples=500, noise=0.30, random_state=42)
plt.figure(figsize=(8, 6))
plt.plot(x[:, 0][y == 0], x[:, 1][y == 0], "D", c="#F9B041")
plt.plot(x[:, 0][y == 1], x[:, 1][y == 1], "o", c="#2DA9E1")
plt.show()
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
plt.figure(figsize=(8, 6))
clf = DecisionTreeClassifier(max_depth=20, random_state=42)
clf.fit(x_train, y_train)
plot_decision_boundary(clf, x, y)
plt.title("Decision border", fontsize=14)
plt.show()
В областях, покрашенных в оранжевый, модель будет классифицировать точки как объекты из класса $0$. В синих — как объекты из класса $1$.
Обратите внимание на странные рваные области на рисунке. В этих областях из-за шума, присутствующего в данных, оказались объекты неправильного класса. Дерево переобучилось под обучающую выборку.
Что произойдет, если мы возьмем разные разбиения данных на обучение и тест для одного и того же датасета?
# first set of points
x_train1, x_test1, y_train1, y_test1 = train_test_split(x, y, random_state=1)
clf1 = DecisionTreeClassifier(max_depth=20, random_state=42)
clf1.fit(x_train1, y_train1)
# second set of points
x_train2, x_test2, y_train2, y_test2 = train_test_split(x, y, random_state=2)
clf2 = DecisionTreeClassifier(max_depth=20, random_state=42)
clf2.fit(x_train2, y_train2)
plt.figure(figsize=(16, 6))
plt.subplot(121)
plot_decision_boundary(clf1, x, y)
plt.title("Decision border 1", fontsize=14)
plt.subplot(122)
plot_decision_boundary(clf2, x, y)
plt.title("Decision border 2", fontsize=14)
plt.show()
Границы решений поменялись. Исчезли одни "рваные" границы и появились другие. Наше дерево неустойчиво, из-за малейшего шума в данных оно может поменять свое предсказание. Оно переобучается на шум в данных.
Говорят, что у нашего дерева высокий variance.
Можно ли что-то поправить?
У нас в настройках максимальная глубина дерева поставлена равной 20. Сделаем дерево глубины 1:
# first set of points
clf1 = DecisionTreeClassifier(max_depth=1, random_state=42)
clf1.fit(x_train1, y_train1)
# second set of points
clf2 = DecisionTreeClassifier(max_depth=1, random_state=42)
clf2.fit(x_train2, y_train2)
plt.figure(figsize=(16, 6))
plt.subplot(121)
plot_decision_boundary(clf1, x, y)
plt.title("Decision border 1", fontsize=14)
plt.subplot(122)
plot_decision_boundary(clf2, x, y)
plt.title("Decision border 2", fontsize=14)
plt.show()
Или глубины 2:
# first set of points
clf1 = DecisionTreeClassifier(max_depth=2, random_state=42)
clf1.fit(x_train1, y_train1)
# second set of points
clf2 = DecisionTreeClassifier(max_depth=2, random_state=42)
clf2.fit(x_train2, y_train2)
plt.figure(figsize=(16, 6))
plt.subplot(121)
plot_decision_boundary(clf1, x, y)
plt.title("Decision border 1", fontsize=14)
plt.subplot(122)
plot_decision_boundary(clf2, x, y)
plt.title("Decision border 2", fontsize=14)
plt.show()
Теперь полученные границы решений (почти) совпадают. Но наше дерево не в состоянии (в обоих случаях) уловить закономерность в исходных данных. Если мы отложим только тренировочный датасет, то увидим следующее:
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
clf1 = DecisionTreeClassifier(max_depth=2, random_state=42)
clf1.fit(x_train, y_train)
clf2 = DecisionTreeClassifier(max_depth=20, random_state=42)
clf2.fit(x_train, y_train)
plt.figure(figsize=(16, 6))
plt.subplot(121)
plot_decision_boundary(clf1, x_train, y_train)
plt.title("Decision border, depth=2, train only", fontsize=14)
plt.subplot(122)
plot_decision_boundary(clf2, x_train, y_train)
plt.title("Decision border, depth=20, train only", fontsize=14)
plt.show()
Мы видим, что в то время как дерево большой глубины выучило нашу тренировочную выборку почти идеально, дерево малой глубины для многих объектов из тренировочной выборки предсказывает не тот класс. Причем, оно не может исправиться просто в силу ограничения на глубину.
В случае дерева с малой глубиной нам не хватает сложности модели, чтобы уловить внутреннюю структуру данных. Говорят, что у нашей модели высокий bias.
Можно показать, что ошибка любой модели раскладывается в сумму трех компонент:
$$ \large \text{Model error} = \text{Bias} + \text{Variance} + \text{Irreducible error} $$Обычно, высокий bias имеют модели, которые недостаточно сложны по сравнению с реальной закономерностью данных. Например, реальная зависимость, которую мы наблюдаем, нелинейная, а мы пытаемся аппроксимировать ее прямой линией. В этом случае наше решение заведомо смещено (biased) в сторону линейной модели, и мы будем систематически ошибаться в сравнении с реальной моделью данных.
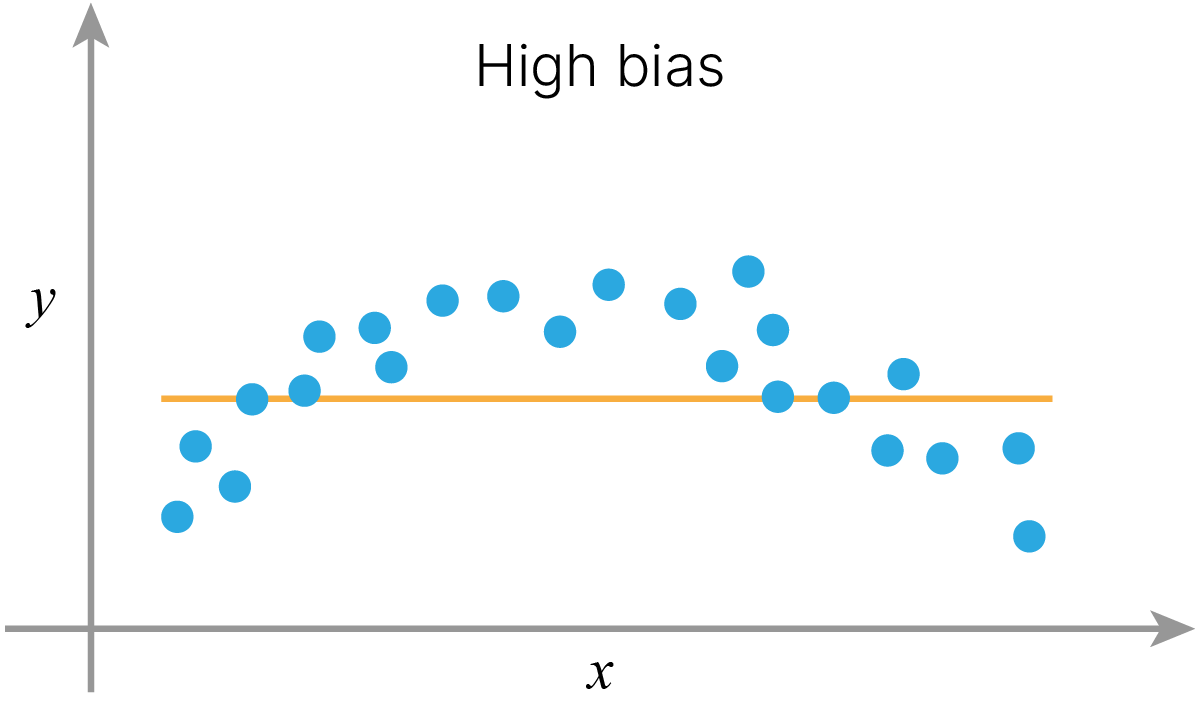
Можно получить и обратную ситуацию. Если модель будет слишком сложная (в смысле своей выразительной способности) и "гибкая", то она сможет подстроиться под данные и выучить тренировочную выборку полностью. В этом случае модель будет подстраиваться под любой шум в данных и пытаться объяснить его какой-то сложной закономерностью.
Малое изменение в данных будет приводить к большим изменениям в прогнозе модели.
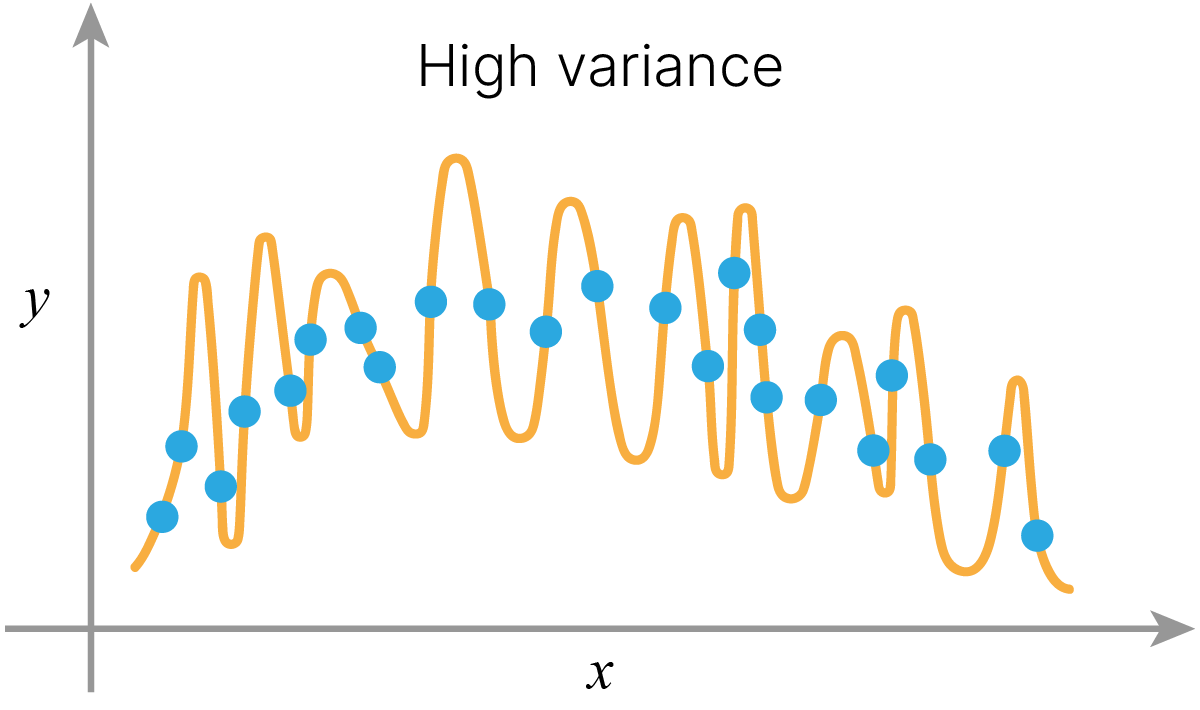
Иногда bias и variance представляют еще таким образом:
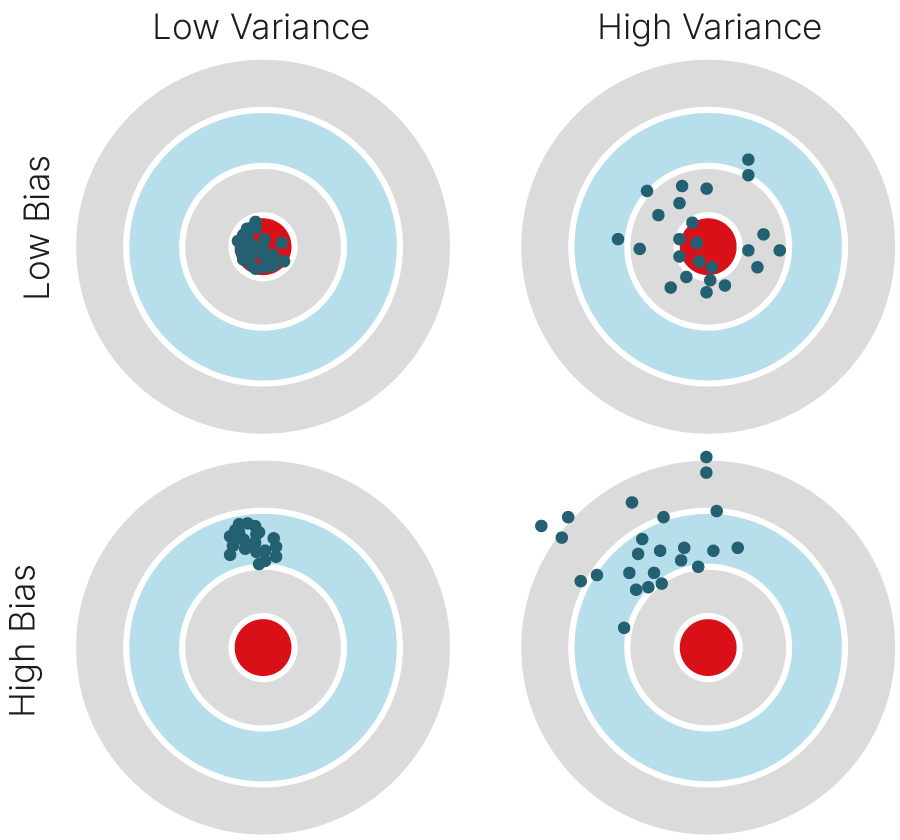
Если удачно подобрать модель и ее гиперпараметры, то гипотетически можно точно предсказать среднее значение ожидаемой величины, то есть получить и низкий $\text{Bias}$, и низкий $\text{Variance}$.
В реальности при измерении физической величины есть случайные непредсказуемые погрешности — отклонения от среднего. Из-за этого предсказания всегда будут иметь определенный уровень ошибки, ниже которого опуститься нельзя — это и есть $\text{Irreducible error}$.

В практических задачах, когда невозможно подобрать реальную модель данных, не получается бесконечно уменьшать и Bias, и Variance — приходится искать компромисс (bias-variance tradeoff). С какого-то момента при уменьшении Bias начнет увеличиваться Variance, и наоборот. Задача исследователя — найти точку оптимума.
Можно построить зависимость этих величин от сложности модели (capacity). По мере увеличения сложности Variance имеет тенденцию к возрастанию, а Bias — к убыванию. Более сложные модели подстраиваются под случайные шумы обучающей выборки, а более простые — не могут воспроизвести реальные закономерности.
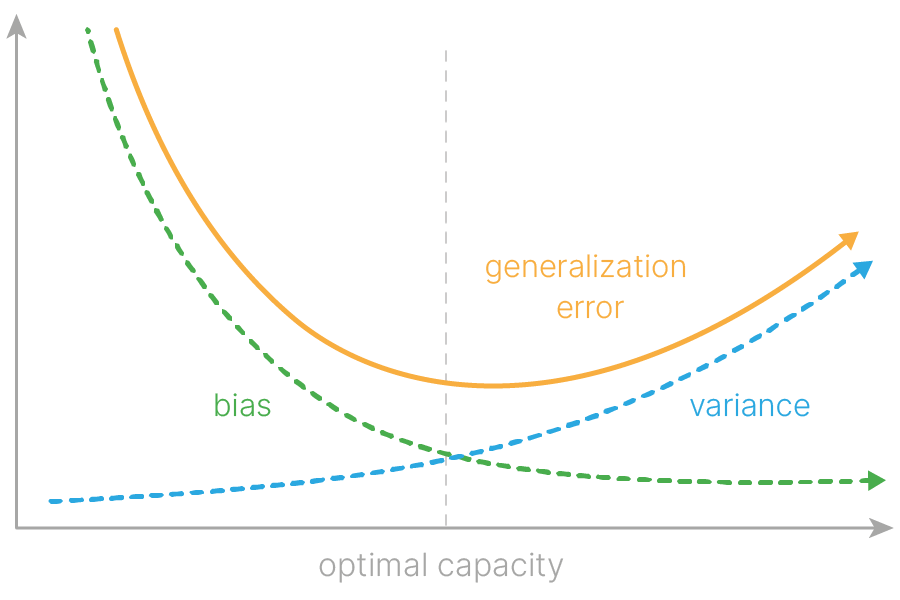
Управлять эффектом variance и bias можно как с помощью выбора модели, так и с помощью выбора гиперпараметров модели.
Продемонстрируем источники компонент Bias и Variance на примере регрессии зашумленной косинусоиды методом k-NN. Создадим функцию для генерации небольшой обучающей выборки и отобразим ее на графике
np.random.seed(42)
num_points = 300
num_grid = 500
x_max = 3.14
plt.figure(figsize=(10, 6))
def get_sample(num_points, x_max, std=0.3, x_sample=None):
if x_sample is None:
x_sample = (np.random.rand(num_points) - 0.5) * 2 * x_max
y_sample = np.cos(x_sample.flatten()) + np.random.randn(x_sample.shape[0]) * std
return x_sample.reshape(-1, 1), y_sample
x_grid = np.linspace(-x_max, x_max, num_grid).reshape(-1, 1)
x_sample, y_sample = get_sample(num_points=num_points, x_max=x_max)
_, y_true = get_sample(num_points=num_points, x_max=x_max, std=0, x_sample=x_grid)
plt.scatter(x_sample, y_sample, c="#bea6ff", label="Noise")
plt.plot(x_grid, y_true, "b--", linewidth=4, label="Real func")
plt.xlabel("X")
plt.ylabel("Y")
plt.legend()
plt.show()
Обучим одну и ту же модель с параметром количества соседей $1$ на разных выборках. Сравним предсказания моделей друг с другом и с реальной целевой функцией.
from sklearn.neighbors import KNeighborsRegressor
np.random.seed(42)
num_points = 30
num_models = 3
plt.figure(figsize=(24, 6))
model = KNeighborsRegressor(n_neighbors=1)
y_pred = np.zeros((num_models, num_grid))
sample_color = ["#00E134", "#FF9100", "#FF00B3"]
for model_num in range(num_models):
x_sample, y_sample = get_sample(num_points=num_points, x_max=x_max)
model.fit(x_sample, y_sample)
y_pred[model_num] = model.predict(x_grid)
_, y_true = get_sample(num_points=num_points, x_max=x_max, std=0, x_sample=x_grid)
plt.subplot(1, 3, model_num + 1)
plt.scatter(
x_sample, y_sample, c=sample_color[model_num], label=f"sample {model_num+1}"
)
plt.plot(
x_grid,
y_pred[model_num],
c=sample_color[model_num],
alpha=0.8,
label=f"model trained on sample {model_num+1}",
)
plt.plot(x_grid, y_true, "b--", linewidth=4, label="real mean")
plt.xlabel("X")
plt.ylabel("Y")
plt.ylim(-1.5, 1.8)
plt.legend(loc="lower center")
Предсказания моделей отличаются друг от друга и от истинной кривой средних значений косинуса.
Обучим 1000 моделей, для разного количества соседей ($1, 3, 25$) на разных подвыборках наших данных. Выберем одну тестовую точку и посмотрим, как предсказания моделей в этой точке зависят от гиперпараметра — количества соседей.
import matplotlib.gridspec as gridspec
num_models = 1000
for n_neighbors in [1, 3, 25]:
model = KNeighborsRegressor(n_neighbors=n_neighbors)
y_pred = np.zeros((num_models, num_grid))
plt.figure(figsize=(10, 4))
gs = gridspec.GridSpec(1, 2, width_ratios=[2, 1])
plt.subplot(gs[0])
for model_num in range(num_models):
x_sample, y_sample = get_sample(num_points=num_points, x_max=x_max)
model.fit(x_sample, y_sample)
y_pred[model_num] = model.predict(x_grid)
plt.plot(x_grid, y_pred[model_num], alpha=0.01, c="g", linewidth=5)
_, y_true = get_sample(num_points=num_points, x_max=x_max, std=0, x_sample=x_grid)
plt.plot(x_grid, y_true, c="b", linewidth=3, label="real mean")
plt.axvline(x=x_grid[num_grid // 2], c="r", linewidth=1, label="X text point")
plt.xlim((-x_max, x_max))
plt.ylim((-1, 2))
plt.xlabel("X")
plt.ylabel("Y")
plt.gca().set_title(f"{num_models} models: {n_neighbors} nearest neighbours")
plt.legend(loc="upper right")
plt.subplot(gs[1])
var = y_pred[:, num_grid // 2].var()
bias = np.abs(y_true[num_grid // 2] - y_pred[:, num_grid // 2].mean())
plt.hist(
y_pred[:, num_grid // 2],
bins=15,
color="g",
alpha=0.5,
orientation="horizontal",
label=f"predictions: \nvar = {var:.2f}\nbias = {bias:.2f}",
)
plt.axhline(y=y_true[num_grid // 2], c="b", linewidth=3, label="real mean")
plt.ylim((-1, 2))
plt.xlabel("hist counts")
plt.ylabel("Y")
plt.gca().set_title(f"predictions at test point")
plt.legend(loc="upper left")
plt.tight_layout()
plt.show()
По мере увеличения числа соседей:
Дерево малой глубины имеет малую сложность и высокий Bias.
Дерево большой глубины имеет высокую сложность и высокий Variance.
Можно подобрать для дерева идеальную capacity, когда Bias и Variance будут суммарно давать наименьший вклад в ошибку. Этим мы занимаемся при подборе параметров. Но есть и другие способы борьбы с Variance и/или Bias, которые мы разберем позже.
Заметим, что если бы мы могли не просто брать решение дерева, а привязывать к этому какую-то статистику, например, сколько деревьев, построенных по подобной процедуре, приняли такое же решение, то мы смогли бы получить более качественное решение.
Если наложить решающие границы 100 решающих деревьев, построенных на разных выборках из $x, y$, то мы увидим, что "хорошие области", соответствующие реальному разделению данных, будут общими между деревьями, а плохие — индивидуальны. К сожалению, в реальности мы не можем брать бесконечное число наборов данных из генеральной совокупности (представленной в данном случае $x, y$)
plt.figure(figsize=(8, 6))
for i in range(1, 101):
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=i)
clf = DecisionTreeClassifier(max_depth=20, random_state=0)
clf.fit(x_train, y_train)
plot_decision_boundary(clf, x, y, alpha=0.02, contour=False)
plt.show()
Мы хотим получить какое-то представление о точности нашей оценки: качества модели, корреляции между двумя переменными и т.д. И мы не знаем, как распределена характеристика, которую мы оцениваем.
Есть много подходов к тому, как получить такую оценку, и один из них — бутстрэп.
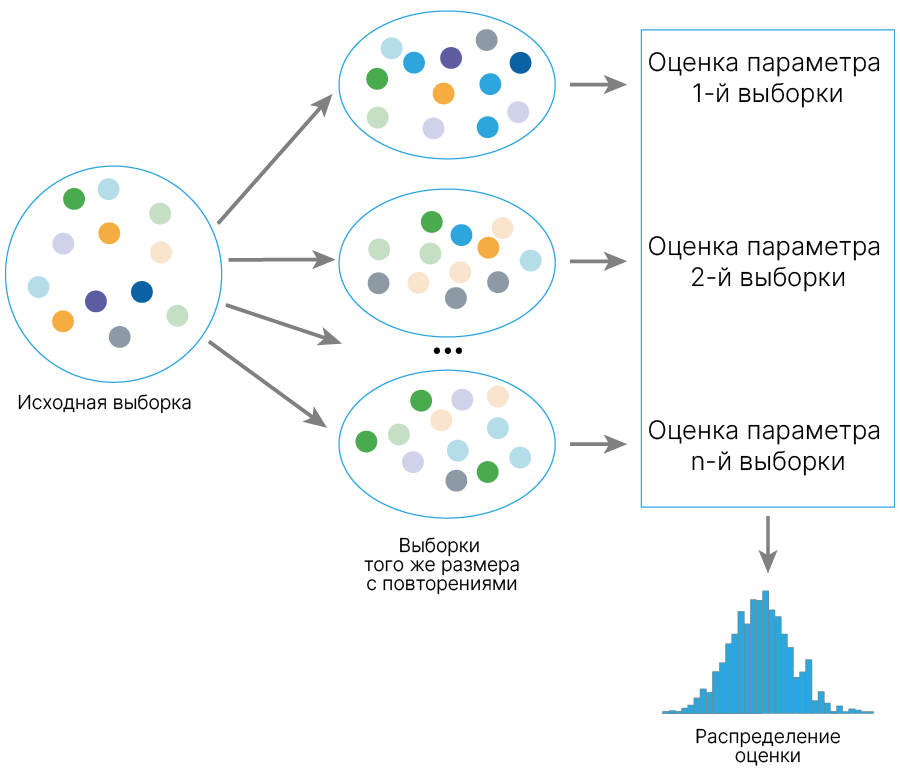
Что мы делаем:
Делаем из нашего исходного датасета N выборок такого же размера с повторениями.
Для каждой полученной выборки (обычно их называют псевдовыборками) считаем характеристику, для которой хотим получить оценку.
В результате такой процедуры получаем N значений характеристики. Строим гистограмму этих значений. Получаем примерное распределение нашей характеристики.
Можем построить 95% доверительный интервал для нашей характеристики. Для этого отрезаем 2.5% самых больших значений и самых малых.
Давайте попробуем сделать это на двух практических примерах.
Подробнее про бутстрэп 🎓[article].
Мы хотим сравнить поведение двух моделей на тестовом датасете. Допустим, нас интересует F1-score. Как нам это сделать?
Сгенерируем данные:
import numpy as np
size = 1500
y = np.random.choice([0, 1], size=size, replace=True)
print(f"shape y: {y.shape}")
print(f"First 10 values: {y[0:10]}")
shape y: (1500,) First 10 values: [1 0 0 0 1 1 0 1 1 1]
Напишем функцию, которая имитирует поведение модели, угадывающей правильный класс в $p$ процентах случаев:
def guess_model(y_real, p):
guessed = np.random.choice([True, False], size=size, replace=True, p=[p, 1 - p])
y_pred = np.zeros_like(y_real)
y_pred[guessed] = y_real[guessed]
y_pred[~guessed] = 1 - y_real[~guessed]
return y_pred
Пусть у нас две модели обладают одинаковым качеством, а третья — лучшим:
model1 = lambda y: guess_model(y, p=0.7)
model2 = lambda y: guess_model(y, p=0.7)
model3 = lambda y: guess_model(y, p=0.75)
np.random.seed(0)
y_pred1 = model1(y)
y_pred2 = model2(y)
y_pred3 = model3(y)
Первый вариант — просто посчитать F1-score каждой модели и проранжировать их в соответствии с F1-score:
from sklearn.metrics import f1_score
qual1 = f1_score(y_true=y, y_pred=y_pred1)
qual2 = f1_score(y_true=y, y_pred=y_pred2)
qual3 = f1_score(y_true=y, y_pred=y_pred3)
print(f" qual1: {qual1:.3f}\n qual2: {qual2:.3f}\n qual3: {qual3:.3f}")
qual1: 0.708 qual2: 0.691 qual3: 0.774
Нужная нам модель выбрана, но почему мы считаем различия между второй и третьей моделью значимыми, а между первой и второй — нет?
print(f"qual2 - qual1: {(qual2 - qual1):.3f}\nqual3 - qual2: {(qual3 - qual2):.3f}")
qual2 - qual1: -0.017 qual3 - qual2: 0.083
Такой способ (при помощи точечной оценки) может привести к ошибке, так как не дает нам судить о значимости отличий.
Существует много способов посчитать значимость данного отличия. Мы рассмотрим способ сравнения на основе bootstrap. Об остальных можете почитать в обзоре, приведенном в списке литературы.
Способ состоит в применении бутстрэпа к предсказаниям модели и реальным меткам.
def bootstrap_metric(x, y, metric_fn, samples_cnt=1000, random_state=42):
np.random.seed(random_state)
b_metric = np.zeros(samples_cnt)
for it in range(samples_cnt):
poses = np.random.choice(x.shape[0], size=x.shape[0], replace=True)
x_boot = x[poses]
y_boot = y[poses]
m_val = metric_fn(x_boot, y_boot)
b_metric[it] = m_val
return b_metric
Так мы сможем получить распределние нашей оценки:
import seaborn as sns
import matplotlib.pyplot as plt
boot_f1score_m1 = bootstrap_metric(
y, y_pred1, metric_fn=lambda x, y: f1_score(y_true=x, y_pred=y)
)
# plot histogram of the obtained values:
plt.figure(figsize=(10, 6))
sns.histplot(boot_f1score_m1)
plt.title("bootstrap f1 scores")
plt.show()
boot_f1score_m1 = bootstrap_metric(
y, y_pred1, metric_fn=lambda x, y: f1_score(y_true=x, y_pred=y)
)
boot_f1score_m2 = bootstrap_metric(
y, y_pred2, metric_fn=lambda x, y: f1_score(y_true=x, y_pred=y)
)
boot_f1score_m3 = bootstrap_metric(
y, y_pred3, metric_fn=lambda x, y: f1_score(y_true=x, y_pred=y)
)
Построим 90% доверительный интервал качества для каждой модели:
alpha = 0.10
print(
"F1 score for the 1st model: ",
np.quantile(boot_f1score_m1, q=[alpha / 2, 1 - alpha / 2]),
)
print(
"F1 score for the 2st model: ",
np.quantile(boot_f1score_m2, q=[alpha / 2, 1 - alpha / 2]),
)
print(
"F1 score for the 3st model: ",
np.quantile(boot_f1score_m3, q=[alpha / 2, 1 - alpha / 2]),
)
F1 score for the 1st model: [0.68614132 0.72807627] F1 score for the 2st model: [0.66925519 0.71175207] F1 score for the 3st model: [0.75284586 0.79355148]
Теперь мы видим, что доверительные интервалы для качества первой и второй модели практически одинаковы, в то время как доверительный интервал для качества третьей модели от них сильно отличается и не пересекается.
Можем построить боксплот (box-plot 📚[wiki]):
import pandas as pd
plt.figure(figsize=(16, 6))
sns.boxplot(
data=pd.DataFrame(
{
"model1": boot_f1score_m1,
"model2": boot_f1score_m2,
"model3": boot_f1score_m3,
}
)
)
plt.ylabel("f1 score", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.show()
Мы могли бы использовать и тест Манна — Уитни 📚[wiki]:
from scipy.stats import mannwhitneyu
statistic_m1_m2, p_value_m1_m2 = mannwhitneyu(boot_f1score_m1, boot_f1score_m2)
statistic_m1_m3, p_value_m1_m3 = mannwhitneyu(boot_f1score_m1, boot_f1score_m3)
statistic_m2_m3, p_value_m2_m3 = mannwhitneyu(boot_f1score_m2, boot_f1score_m3)
# fmt: off
print(f"m1 and m2 Mann–Whitney statistic: {statistic_m1_m2:<10} p-value:{p_value_m1_m2}")
print(f"m1 and m3 Mann–Whitney statistic: {statistic_m1_m3:<10} p-value:{p_value_m1_m3}")
print(f"m2 and m3 Mann–Whitney statistic: {statistic_m2_m3:<10} p-value:{p_value_m2_m3}")
# fmt: on
m1 and m2 Mann–Whitney statistic: 819172.5 p-value:7.059998764073036e-135 m1 and m3 Mann–Whitney statistic: 51.0 p-value:0.0 m2 and m3 Mann–Whitney statistic: 2.0 p-value:0.0
Видим, что результат идентичен. В дальнейшем мы будем использовать только графки для оценки, но на практике полезно использовать несколько способов, чтобы избежать ошибочных суждений.
Рассмотрим на другом примере, используя данные о людях с наличием или отсутствием сердечных заболеваний. Загрузим датасет Heart Disease 🛠️[doc].
heart_dataset = pd.read_csv(
"https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/heart.csv"
)
from sklearn.model_selection import train_test_split
x = heart_dataset.drop("target", axis=1)
y = heart_dataset["target"] > 0
x_train, x_test, y_train, y_test = train_test_split(x, y.values, random_state=42)
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import GridSearchCV
svc_model = GridSearchCV(
SVC(), {"kernel": ("linear", "rbf"), "C": [0.01, 0.1, 1, 10]}
).fit(x_train, y_train)
logr_model = GridSearchCV(
LogisticRegression(solver="liblinear", max_iter=100000),
{"penalty": ("l1", "l2"), "C": [0.01, 0.1, 1, 10, 100]},
).fit(x_train, y_train)
# few objects in the leaf - poor estimates of class probabilities - the model is overfitting
dt_model = GridSearchCV(
DecisionTreeClassifier(),
{"max_depth": [1, 3, 5, 7, 10], "min_samples_leaf": [1, 3, 5, 10]},
).fit(x_train, y_train)
from sklearn.metrics import average_precision_score # PR-AUC
y_pred1 = svc_model.decision_function(
x_test
) # by default, SVM gives score to each object instead of probabilities
y_pred2 = logr_model.predict_proba(x_test)[:, 1]
y_pred3 = dt_model.predict_proba(x_test)[:, 1]
qual1 = average_precision_score(y_true=y_test, y_score=y_pred1)
qual2 = average_precision_score(y_true=y_test, y_score=y_pred2)
qual3 = average_precision_score(y_true=y_test, y_score=y_pred3)
print(f"Logistic regression pr-auc: {qual1:.03f}")
print(f"SVC pr-auc: {qual2:.03f}")
print(f"DecisionTreeClassifier pr-auc: {qual3:.03f}")
Logistic regression pr-auc: 0.893 SVC pr-auc: 0.902 DecisionTreeClassifier pr-auc: 0.801
Теперь подсчитаем бутстрэп-оценки. Обратите внимание на то, что теперь мы передаем не предсказания, а вероятности.
boot_score_logreg = bootstrap_metric(
y_test, y_pred1, metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y)
)
boot_score_svc = bootstrap_metric(
y_test, y_pred2, metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y)
)
boot_score_dt = bootstrap_metric(
y_test, y_pred3, metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y)
)
alpha = 0.10
print(
"Logistic regression pr-auc 90%-ci: ",
np.quantile(boot_score_logreg, q=[alpha / 2, 1 - alpha / 2]),
)
print("SVC pr-auc 90%-ci:", np.quantile(boot_score_svc, q=[alpha / 2, 1 - alpha / 2]))
print(
"DecisionTreeClassifier pr-auc 90%-ci:",
np.quantile(boot_score_dt, q=[alpha / 2, 1 - alpha / 2]),
)
Logistic regression pr-auc 90%-ci: [0.80793003 0.97363727] SVC pr-auc 90%-ci: [0.8276533 0.97115084] DecisionTreeClassifier pr-auc 90%-ci: [0.70049707 0.90513571]
Видим, что качество SVC и логистической регрессии почти не отличается, а дерево решений уступает обеим моделям.
plt.figure(figsize=(16, 6))
sns.boxplot(
data=pd.DataFrame(
{"Log-reg": boot_score_logreg, "SVC": boot_score_svc, "DT": boot_score_dt}
)
)
plt.ylabel("PR-AUC", size=20)
plt.xlabel("Base models", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.show()
Пусть у нас есть сигнал:
1110110011
Но при передаче на другое устройство в нем могут возникать ошибки:
1010111011
Самое простое решение возникшей проблемы:
1010111011
1110010011
11001101 11
1110110011
Напишем код, чтобы удостовериться в наших выводах.
import numpy as np
def get_signal(size, random_state=42):
signal = np.random.choice([0, 1], size, replace=True)
return signal
def compare_signs(sig1, sig2):
return (sig1 != sig2).sum()
def add_noise(sig, noise_p=0.20):
sig = sig.copy()
changed = np.random.choice(
[True, False], sig.shape[0], replace=True, p=[noise_p, 1 - noise_p]
)
sig[changed] = 1 - sig[changed]
return sig
def average_signals(sigs):
sig = np.mean(sigs, axis=0)
sig = np.round(sig, 0)
return sig
def send_signal(signal, tries):
passed_sigs = [add_noise(signal) for _ in range(tries)]
fin_signal = average_signals(passed_sigs)
return fin_signal
import matplotlib.pyplot as plt
np.random.seed(42)
repeats = 1000
signals_cnt_rng = range(1, 30, 2)
signal = get_signal(10)
mistakes = np.zeros((repeats, len(signals_cnt_rng)))
for j, sig_cnt in enumerate(signals_cnt_rng):
for i in range(repeats):
rec_sig = send_signal(signal, sig_cnt)
mistakes[i, j] = compare_signs(rec_sig, signal)
mn = mistakes.mean(axis=0)
sd = mistakes.std(axis=0)
plt.figure(figsize=(10, 5))
plt.title("Number of error in signal", fontsize=14)
plt.ylabel("Number of errors", fontsize=14)
plt.xlabel("Number of signals passed at once", fontsize=14)
plt.plot(signals_cnt_rng, mn)
plt.fill_between(signals_cnt_rng, mn - sd, mn + sd, facecolor="blue", alpha=0.1)
plt.show()
Оказывается, это имеет отношение к проблеме, с которой мы столкнулись с деревьями решений.
Постановка задачи:
Есть 10 объектов, в реальности все принадлежат классу 1
1111111111
Пусть у нас есть три независимых классификатора A, B и C. Каждый предсказывает 1 в 70% случаев.
Мы хотим получить общий классификатор на основании этих трех.
Мы хотим получить предсказание базовых классификаторов и применить к ним какую-то функцию, которая выдаст итоговый ответ. Вид этой функции задается заранее.
Будем просто усреднять предсказание наших классификаторов
$$\large h(x) = \dfrac 1 T \sum_{i=1}^{T}a_i(x) $$Простое голосование

Посчитаем вероятность того, что:
Таким образом, если брать большинство голосов, то мы будем в 78% случаев предсказывать верно. Мы взяли 3 классификатора, которые сами по себе были не очень хорошими, и получили классификатор лучшего качества. Если взять больше классификаторов, то ситуация будет еще лучше.
Пусть теперь у нас три классификатора, выдающие следующие предсказания
1111111100 — $80\%$ точность
1111111100 — $80\%$ точность
1</font>011111100 — $70\%$ точность
Если объединим предсказания, то получим:
1111111100 — $80\%$ точность
Потому что очень высокая зависимость предсказаний. Выше видно, что два классификатора предсказывают абсолютно одинаково. Вероятность, что они делают это случайно, очень мала.
А вот если возьмем такие классификаторы, то все получится:
1111111100 — $80\%$ точность
0111011101 — $70\%$ точность
1000101111 — $60\%$ точность
Усреднение:
1111111101 — $90\%$ точность
def get_predictions(y_real, p, cnt):
size = y_real.shape[0]
guessed = np.random.choice([True, False], (cnt, size), p=[p, 1 - p])
y = np.repeat(y_real.reshape(1, -1), cnt, axis=0)
y[~guessed] = 1 - y[~guessed]
return y
import pandas as pd
import seaborn as sns
size = 1000
reps = 10
cnt_base_predictors = [1] + list(range(5, 105, 5))
single_qual = [0.45, 0.5, 0.51, 0.55, 0.6, 0.75, 0.9]
dt = {"cnt": [], "single_qual": [], "accuracy": []}
for i in range(reps):
y_real = np.random.choice([0, 1], size)
for cnt in cnt_base_predictors:
for p in single_qual:
preds = get_predictions(y_real, p, cnt)
voting = np.round(preds.mean(axis=0))
accuracy = (y_real == voting).mean()
dt["cnt"].append(cnt)
dt["single_qual"].append(f"{p:.02}")
dt["accuracy"].append(accuracy)
results = pd.DataFrame(dt)
plt.figure(figsize=(16, 6))
sns.lineplot(data=results, x="cnt", y="accuracy", hue="single_qual", lw=3, alpha=0.5)
plt.xlabel("Number of base classifiers", size=20)
plt.ylabel("Accuracy", size=20)
plt.legend(loc="best", fontsize=12, title="Single classifier quality")
plt.show()
Видим, что:
Посмотрим, как зависит качество предсказания от коррелированности предсказателей. Конкретно — от ожидаемой коррелированности вероятностей ошибиться на данном объекте для любой взятой пары классификаторов из ансамбля.
import scipy
def get_correlated_predictions(y_real, p, cnt, r):
size = y_real.shape[0]
x1 = np.random.uniform(0, 1, size)
x2 = np.random.uniform(0, 1, (cnt, size))
q = np.sqrt(r)
y = q * x1 + (1 - q**2) ** 0.5 * x2 # y variables now correlated with correlation=r
y_mod = np.zeros_like(y)
for i in range(y.shape[0]):
y_mod[i] = scipy.stats.rankdata(y[i])
y = y_mod / size # back to uniform, slightly affects correlations
y_pred = np.repeat(y_real.reshape(1, -1), cnt, axis=0)
y_pred[y < 1 - p] = 1 - y_pred[y < 1 - p] # to predictions, affects correlations
return y_pred
np.random.seed(42)
x = np.arange(0, 1, 0.05)
accuracy = np.zeros_like(x)
p = 0.7
cnt = 100
for ind, r in enumerate(x):
preds = get_correlated_predictions(y_real, p, cnt, r)
voting = np.round(preds.mean(axis=0))
accuracy[ind] = (y_real == voting).mean()
plt.figure(figsize=(16, 6))
plt.title(f"Accuracy of {cnt} classifiers ensemble", size=20)
plt.xlabel("Correlation among classifiers", size=20)
plt.ylabel("Accuracy", size=20)
plt.axhline(y=p, color="red", lw=5, ls="--", label="Single classifier")
sns.lineplot(x=x, y=accuracy, lw=5, label="Ensemble")
plt.legend(fontsize=20)
plt.show()
Видим, что по мере увеличения коррелированности моделей качество все больше и больше приближается к качеству одной базовой модели.
Нам нужны классификаторы, которые сами по себе предсказывают лучше, чем случайные, при этом они должны быть не коррелированы. На самом деле это нетривиальная задача: откуда нам брать разные классификаторы, если у нас один датасет?

Первый вариант — нам поможет уже рассмотренный bootstrap:
Делаем из нашего исходного датасета N выборок такого же размера с повторениями.
На каждой псевдовыборке строим отдельную модель. Чтобы полученные модели были слабо зависимы, будем использовать алгоритм, который чувствителен к небольшим изменениям в выборке.
Получаем N слабо зависимых моделей.
Когда нам нужно сделать предсказание для нового объекта, делаем предсказание каждой из N моделей, а затем усредняем предсказание.
В sklearn для бэггинга можно использовать класс BaggingClassifier из sklearn.ensemble. Мы напишем свой код для бэггинга для большей наглядности происходящего.
import sklearn
def get_bootstrap_sample(x, y):
size = x.shape[0]
poses = np.random.choice(size, size=size, replace=True)
x_boot = x[poses]
y_boot = y[poses]
return x_boot, y_boot
class BaggingBinaryClassifierEnsemble:
def __init__(self, base_classifier, ensemble_size, random_state=42):
self.base_classifier = base_classifier
self.ensemble_size = ensemble_size
self.random_state = random_state
self.ensemble = []
def fit(self, x, y):
np.random.seed(self.random_state)
for est_id in range(self.ensemble_size):
x_boot, y_boot = get_bootstrap_sample(x, y)
model = sklearn.clone(self.base_classifier) # create new base model
model.fit(x_boot, y_boot)
self.ensemble.append(model)
def predict_proba(self, x):
if not self.ensemble:
raise Exception("Unfitted model")
y_pred = 0
for est in self.ensemble:
y_pred += est.predict(x)
y_pred = y_pred / self.ensemble_size
return y_pred
def predict(self, x):
y_proba = self.predict_proba(x)
y_pred = np.round(y_proba)
return y_pred
Для простоты здесь и далее будем использовать параметры моделей, подобранные ранее, когда мы использовали их вне ансамбля. В данном случае это не имеет значения, но в случае разбираемых далее случайного леса и градиентного бустинга параметры подбирают вместе с построением ансамбля.
heart_dataset = pd.read_csv(
"https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/heart.csv"
)
from sklearn.model_selection import train_test_split
x = heart_dataset.drop("target", axis=1)
y = heart_dataset["target"] > 0
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import GridSearchCV
svc_model = GridSearchCV(
SVC(), {"kernel": ("linear", "rbf"), "C": [0.01, 0.1, 1, 10]}
).fit(x_train, y_train)
logr_model = GridSearchCV(
LogisticRegression(solver="liblinear", max_iter=100000),
{"penalty": ("l1", "l2"), "C": [0.01, 0.1, 1, 10, 100]},
).fit(x_train, y_train)
# few objects in the leaf - poor estimates of class probabilities - the model is overtraining
dt_model = GridSearchCV(
DecisionTreeClassifier(),
{"max_depth": [1, 3, 5, 7, 10], "min_samples_leaf": [1, 3, 5, 10]},
).fit(x_train, y_train)
Опробуем модель:
bagging_dt = BaggingBinaryClassifierEnsemble(
dt_model.best_estimator_, ensemble_size=100
)
bagging_logreg = BaggingBinaryClassifierEnsemble(
logr_model.best_estimator_, ensemble_size=100
)
bagging_svc = BaggingBinaryClassifierEnsemble(
svc_model.best_estimator_, ensemble_size=100
)
bagging_dt.fit(x_train.values, y_train.values)
bagging_logreg.fit(x_train.values, y_train.values)
bagging_svc.fit(x_train.values, y_train.values)
y_pred_blr = bagging_logreg.predict_proba(x_test.values)
y_pred_bsvc = bagging_svc.predict_proba(x_test.values)
y_pred_bdt = bagging_dt.predict_proba(x_test.values)
from sklearn.metrics import average_precision_score # PR-AUC
qual_blr = average_precision_score(y_true=y_test, y_score=y_pred_blr)
qual_bsvc = average_precision_score(y_true=y_test, y_score=y_pred_bsvc)
qual_bdt = average_precision_score(y_true=y_test, y_score=y_pred_bdt)
print(f"Bagged Logistic regression pr-auc: {qual_blr:.03f}")
print(f"Bagged SVC pr-auc: {qual_bsvc :.03f}")
print(f"Bagged DecisionTreeClassifier pr-auc: {qual_bdt:.03f}")
Bagged Logistic regression pr-auc: 0.872 Bagged SVC pr-auc: 0.900 Bagged DecisionTreeClassifier pr-auc: 0.898
def bootstrap_metric(x, y, metric_fn, samples_cnt=1000, alpha=0.05, random_state=42):
size = len(x)
np.random.seed(random_state)
b_metric = np.zeros(samples_cnt)
for it in range(samples_cnt):
poses = np.random.choice(x.shape[0], size=x.shape[0], replace=True)
x_boot = x[poses]
y_boot = y[poses]
m_val = metric_fn(x_boot, y_boot)
b_metric[it] = m_val
return b_metric
boot_score_blogreg = bootstrap_metric(
y_test.values,
y_pred_blr,
metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y),
)
boot_score_bsvc = bootstrap_metric(
y_test.values,
y_pred_bsvc,
metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y),
)
boot_score_bdt = bootstrap_metric(
y_test.values,
y_pred_bdt,
metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y),
)
alpha = 0.10
print(
"Bagged Logistic regression pr-auc 90%-ci: ",
np.quantile(boot_score_blogreg, q=[alpha / 2, 1 - alpha / 2]),
)
print(
"Bagged SVC pr-auc 90%-ci:",
np.quantile(boot_score_bsvc, q=[alpha / 2, 1 - alpha / 2]),
)
print(
"Bagged DecisionTreeClassifier pr-auc 90%-ci:",
np.quantile(boot_score_bdt, q=[alpha / 2, 1 - alpha / 2]),
)
Bagged Logistic regression pr-auc 90%-ci: [0.78262498 0.95069418] Bagged SVC pr-auc 90%-ci: [0.81964811 0.9761168 ] Bagged DecisionTreeClassifier pr-auc 90%-ci: [0.83053272 0.95963424]
y_pred1 = svc_model.decision_function(
x_test
) # by default, SVM gives score to each object instead of probabilities
y_pred2 = logr_model.predict_proba(x_test)[:, 1]
y_pred3 = dt_model.predict_proba(x_test)[:, 1]
qual1 = average_precision_score(y_true=y_test, y_score=y_pred1)
qual2 = average_precision_score(y_true=y_test, y_score=y_pred2)
qual3 = average_precision_score(y_true=y_test, y_score=y_pred3)
boot_score_logreg = bootstrap_metric(
y_test.values,
y_pred1,
metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y),
)
boot_score_svc = bootstrap_metric(
y_test.values,
y_pred2,
metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y),
)
boot_score_dt = bootstrap_metric(
y_test.values,
y_pred3,
metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y),
)
plt.figure(figsize=(11, 6))
result_arrays = [
boot_score_logreg,
boot_score_svc,
boot_score_dt,
boot_score_blogreg,
boot_score_bsvc,
boot_score_bdt,
]
base_models = ["Log-Reg", "SVC", "DT"] * 2
ensemble_types = ["Single"] * 3 + ["Bagged"] * 3
dfs = []
for i, res in enumerate(result_arrays):
df = pd.DataFrame(res, columns=["pr_auc"])
df["base_model"] = base_models[i]
df["ensemble_method"] = ensemble_types[i]
dfs.append(df)
sns.boxplot(data=pd.concat(dfs), y="pr_auc", x="base_model", hue="ensemble_method")
plt.xlabel("Base models", size=20)
plt.ylabel("PR-AUC", size=20)
plt.legend(fontsize=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.show()
Дереву решений — при ансамблировании удается получить качество не хуже других базовых моделей.
from sklearn import datasets
x, y = sklearn.datasets.make_moons(n_samples=500, noise=0.30, random_state=42)
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
from matplotlib.colors import ListedColormap
def plot_decision_boundary(
clf, x, y, axes=[-1.5, 2.5, -1, 1.5], alpha=0.85, contour=True, bolded=False
):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
x_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(x_new).reshape(x1.shape)
custom_cmap = ListedColormap(["#FEE7D0", "#bea6ff", "#B8E1EC"])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
if contour:
custom_cmap2 = ListedColormap(["#FEE7D0", "#5D5DA6", "#B8E1EC"])
if bolded:
custom_cmap2 = ListedColormap(["#FEE7D0", "#5D5DA6", "#000000"])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2)
plt.plot(x[:, 0][y == 0], x[:, 1][y == 0], "D", c="#F9B041", alpha=alpha)
plt.plot(x[:, 0][y == 1], x[:, 1][y == 1], "o", c="#2DA9E1", alpha=alpha)
plt.axis(axes)
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
plt.figure(figsize=(16, 6))
plt.subplot(121)
clf = DecisionTreeClassifier(max_depth=10, random_state=42)
clf.fit(x_train, y_train)
plot_decision_boundary(clf, x, y)
plt.title("Single Decision Tree", fontsize=14)
plt.subplot(122)
bagging_dt = BaggingBinaryClassifierEnsemble(
DecisionTreeClassifier(max_depth=10), ensemble_size=100
)
bagging_dt.fit(x_train, y_train)
plot_decision_boundary(bagging_dt, x, y)
plt.title("Bagged Decision Tree", fontsize=14)
plt.show()
Видим, что разделяющая плоскость для дерева более гладкая и лучше отражает реальное разделение классов.
Второй вариант получения псевдовыборок — сэмплировать не объекты, а признаки. При этом бесполезно иметь в выборке два одинаковых признака, так как потом мы делаем выборки меньшего размера, чем исходное число признаков и без повторений.
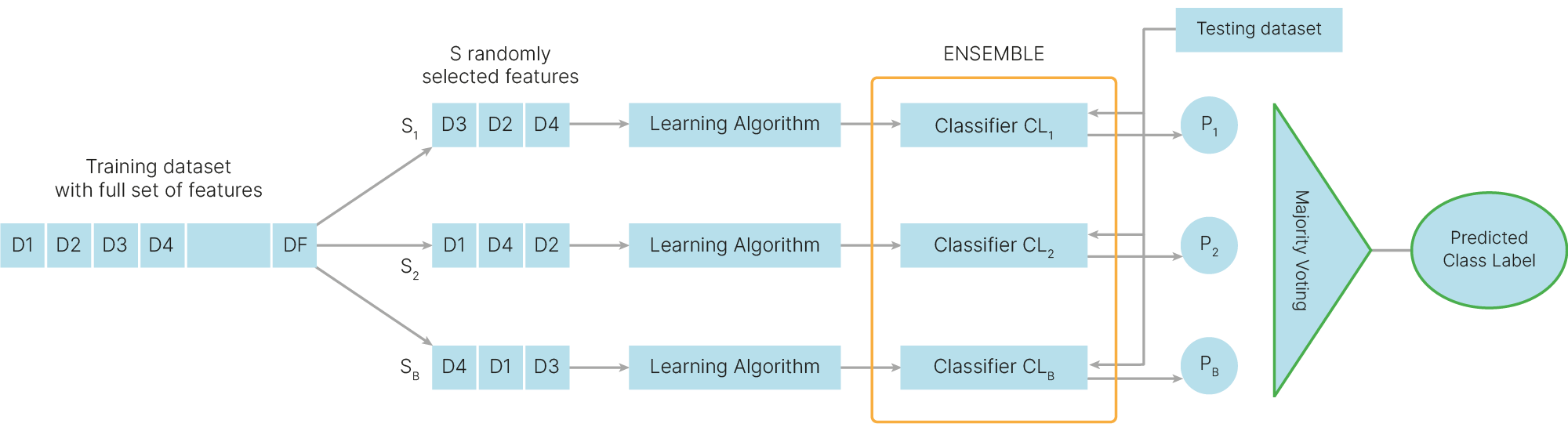
Обычно для каждой модели выбирают:
для задач классификации:
$$\sqrt{\text{feature_cnt}}$$
для задач регрессии:
$$ \frac {\text{feature_cnt}} {3}$$
Хотя строгих правил нет, этот параметр можно подбирать на кросс-валидации.
Напишем метод случайных подпространств сами:
def get_rsm_sample(x, y, f_num=None):
size = x.shape[1]
f_num = f_num or int(np.sqrt(size)) + 1
f_num = min(size, f_num)
f_poses = np.random.choice(size, size=f_num, replace=False)
x_rsm = x[:, f_poses]
y_rsm = y.copy()
return x_rsm, y_rsm, f_poses
class RSMBinaryClassifierEnsemble:
def __init__(
self, base_classifier, ensemble_size, random_state=42, max_features=None
):
self.base_classifier = base_classifier
self.ensemble_size = ensemble_size
self.random_state = random_state
self.max_features = max_features
self.ensemble = []
self.feature_poses = []
# we had to keep track of features selected. In sklearn Random Forest, discussed below,
# another, more stable implementation is used.
# they use `f_num` random features but in case no good split found, they try other features too.
def fit(self, x, y):
np.random.seed(self.random_state)
for est_id in range(self.ensemble_size):
x_boot, y_boot, f_poses = get_rsm_sample(x, y, f_num=self.max_features)
self.feature_poses.append(f_poses)
model = sklearn.clone(self.base_classifier) # create new base model
model.fit(x_boot, y_boot)
self.ensemble.append(model)
def predict_proba(self, x):
if not self.ensemble:
raise Exception("Unfitted model")
y_pred = 0
for ind, est in enumerate(self.ensemble):
y_pred += est.predict(x[:, self.feature_poses[ind]])
y_pred = y_pred / self.ensemble_size
return y_pred
def predict(self, x):
y_proba = self.predict_proba(x)
y_pred = np.round(y_proba)
return y_pred
x = heart_dataset.drop("target", axis=1)
y = heart_dataset["target"] > 0
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
rsm_dt = RSMBinaryClassifierEnsemble(dt_model.best_estimator_, ensemble_size=100)
rsm_logreg = RSMBinaryClassifierEnsemble(logr_model.best_estimator_, ensemble_size=100)
rsm_svc = RSMBinaryClassifierEnsemble(svc_model.best_estimator_, ensemble_size=100)
rsm_dt.fit(x_train.values, y_train.values)
rsm_logreg.fit(x_train.values, y_train.values)
rsm_svc.fit(x_train.values, y_train.values)
y_pred_rlr = rsm_logreg.predict_proba(x_test.values)
y_pred_rsvc = rsm_svc.predict_proba(x_test.values)
y_pred_rdt = rsm_dt.predict_proba(x_test.values)
boot_score_rlogreg = bootstrap_metric(
y_test.values,
y_pred_rlr,
metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y),
)
boot_score_rsvc = bootstrap_metric(
y_test.values,
y_pred_rsvc,
metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y),
)
boot_score_rdt = bootstrap_metric(
y_test.values,
y_pred_rdt,
metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y),
)
alpha = 0.10
print(
"RSM Logistic regression pr-auc 90%-ci: ",
np.quantile(boot_score_blogreg, q=[alpha / 2, 1 - alpha / 2]),
)
print(
"RSM SVC pr-auc 90%-ci:", np.quantile(boot_score_bsvc, q=[alpha / 2, 1 - alpha / 2])
)
print(
"RSM DecisionTreeClassifier pr-auc 90%-ci:",
np.quantile(boot_score_bdt, q=[alpha / 2, 1 - alpha / 2]),
)
RSM Logistic regression pr-auc 90%-ci: [0.78262498 0.95069418] RSM SVC pr-auc 90%-ci: [0.81964811 0.9761168 ] RSM DecisionTreeClassifier pr-auc 90%-ci: [0.83053272 0.95963424]
plt.figure(figsize=(14, 6))
result_arrays = [
boot_score_logreg,
boot_score_svc,
boot_score_dt,
boot_score_blogreg,
boot_score_bsvc,
boot_score_bdt,
boot_score_rlogreg,
boot_score_rsvc,
boot_score_rdt,
]
base_models = ["Log-Reg", "SVC", "DT"] * 3
ensemble_types = ["Single"] * 3 + ["Bagged"] * 3 + ["RSM"] * 3
dfs = []
for i, res in enumerate(result_arrays):
df = pd.DataFrame(res, columns=["pr_auc"])
df["base_model"] = base_models[i]
df["ensemble_method"] = ensemble_types[i]
dfs.append(df)
sns.boxplot(data=pd.concat(dfs), y="pr_auc", x="base_model", hue="ensemble_method")
plt.xlabel("Base model", size=20)
plt.ylabel("PR-AUC", size=20)
plt.legend(fontsize=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.show()
RSM значительно помогает только дереву решений. Остальные методы почти не улучшают своего качества.
Можно объединить оба способа: применяем bootstrap к объектам (получается выборка одного размера, но с повторяющимися объектами, а каких-то объектов не будет), и, кроме этого, выкидываем часть признаков. В этом случае мы получим еще более сильно отличающиеся друг от друга случайные выборки.
sklearn.ensemble.BaggingClassifier и sklearn.ensemble.BaggingRegressor вопреки названию могут поддерживать оба способа.

Теперь будем использовать BaggingClassier из стандартной библиотеки:
from sklearn.ensemble import BaggingClassifier
models = {}
logr_model = GridSearchCV(
LogisticRegression(solver="liblinear", max_iter=100000),
{"penalty": ("l1", "l2"), "C": [0.01, 0.1, 1, 10, 100]},
).fit(x_train, y_train)
models["LogReg"] = logr_model
svc_model = GridSearchCV(
SVC(), {"kernel": ("linear", "rbf"), "C": [0.01, 0.1, 1, 10]}
).fit(x_train, y_train)
models["SVC"] = svc_model
# few objects in the leaf - poor estimates of class probabilities - the model is overtraining
dt_model = GridSearchCV(
DecisionTreeClassifier(),
{"max_depth": [1, 3, 5, 7, 10], "min_samples_leaf": [1, 3, 5, 10]},
).fit(x_train, y_train)
models["DT"] = dt_model
bagging_logr = BaggingClassifier(
logr_model.best_estimator_, n_estimators=100, random_state=42
)
models["Bagging LogReg"] = bagging_logr
bagging_svc = BaggingClassifier(
svc_model.best_estimator_, n_estimators=100, random_state=42
)
models["Bagging SVC"] = bagging_svc
bagging_dt = BaggingClassifier(
dt_model.best_estimator_, n_estimators=100, random_state=42
)
models["Bagging DT"] = bagging_dt
sqrt_features = int(np.sqrt(x.shape[1])) + 1
rsm_logreg = BaggingClassifier(
logr_model.best_estimator_,
n_estimators=100,
bootstrap=False,
max_features=sqrt_features,
random_state=42,
)
models["RSM LogReg"] = rsm_logreg
rsm_svc = BaggingClassifier(
svc_model.best_estimator_,
n_estimators=100,
bootstrap=False,
max_features=sqrt_features,
random_state=42,
)
models["RSM SVC"] = rsm_svc
rsm_dt = BaggingClassifier(
dt_model.best_estimator_,
n_estimators=100,
bootstrap=False,
max_features=sqrt_features,
random_state=42,
)
models["RSM DT"] = rsm_dt
# Both Bagging and RSM
bag_rsm_logreg = BaggingClassifier(
logr_model.best_estimator_,
n_estimators=100,
bootstrap=True,
max_features=sqrt_features,
random_state=42,
)
models["BagRSM LogReg"] = bag_rsm_logreg
bag_rsm_svc = BaggingClassifier(
svc_model.best_estimator_,
n_estimators=100,
bootstrap=True,
max_features=sqrt_features,
random_state=42,
)
models["BagRSM SVC"] = bag_rsm_svc
bag_rsm_dt = BaggingClassifier(
dt_model.best_estimator_,
n_estimators=100,
bootstrap=True,
max_features=sqrt_features,
random_state=42,
)
models["BagRSM DT"] = bag_rsm_dt
for name, model in models.items():
model.fit(x_train, y_train)
predictions = {}
for name, model in models.items():
if name != "SVC":
y_pred = model.predict_proba(x_test)[:, 1]
else:
y_pred = model.decision_function(x_test)
predictions[name] = y_pred
boot_scores = {}
for name, y_pred in predictions.items():
boot_score = bootstrap_metric(
y_test.values,
y_pred,
metric_fn=lambda x, y: average_precision_score(y_true=x, y_score=y),
)
boot_scores[name] = boot_score
plt.figure(figsize=(16, 6))
base_models = ["Log-Reg", "SVC", "DT"] * 4
ensemble_types = ["Single"] * 3 + ["Bagged"] * 3 + ["RSM"] * 3 + ["BagRSM"] * 3
dfs = []
for i, model_name in enumerate(boot_scores):
df = pd.DataFrame(boot_scores[model_name], columns=["pr_auc"])
df["base_model"] = base_models[i]
df["ensemble_method"] = ensemble_types[i]
dfs.append(df)
sns.boxplot(data=pd.concat(dfs), y="pr_auc", x="base_model", hue="ensemble_method")
plt.xlabel("Base model", size=20)
plt.ylabel("PR-AUC", size=20)
plt.legend(fontsize=20, loc="lower right")
plt.tick_params(axis="both", which="major", labelsize=14)
plt.show()
Существенное улучшение качества наблюдается только при использовании решающего дерева в качестве базовой модели.
Чтобы простое голосование повышало качество ансамбля, необходимо, чтобы ошибки базовых моделей не коррелировали между собой.
Попробуем оценить попарную корреляцию в ошибках базовых моделей в ансамблях.
import itertools
def base_model_pair_correlation(ensemble, x):
corrs = []
for (i, est1), (j, est2) in itertools.combinations(
enumerate(ensemble.estimators_), 2
):
xi_test = x.values[:, ensemble.estimators_features_[i]]
xj_test = x.values[:, ensemble.estimators_features_[j]]
if not isinstance(est1, sklearn.svm.SVC):
y_pred_t1 = est1.predict_proba(xi_test)[:, 1]
y_pred_t2 = est2.predict_proba(xj_test)[:, 1]
else:
y_pred_t1 = est1.decision_function(xi_test)
xj_test = x_test.values[:, ensemble.estimators_features_[j]]
y_pred_t2 = est2.decision_function(xj_test)
corrs.append(scipy.stats.pearsonr(y_pred_t1, y_pred_t2)[0])
return np.array(corrs)
pair_correlations = {}
for name, model in models.items():
if not "Bagging" in name and not "RSM" in name:
continue
pair_correlations[name] = base_model_pair_correlation(model, x_test)
cor_res = pd.DataFrame(pair_correlations)
cor_res = cor_res.melt(
value_vars=cor_res.columns, value_name="paircor", var_name="model"
)
# get base models and ensembling methods from names
def read_base(s):
if "dt" in s.lower():
return "DT"
elif "svc" in s.lower():
return "SVC"
else:
return "Log-Reg"
def read_ensemble(s):
bag, rsm = False, False
if "bag" in s.lower():
bag = True
if "rsm" in s.lower():
rsm = True
if bag and rsm:
return "BagRSM"
if bag:
return "Bagged"
if rsm:
return "RSM"
return "Single"
cor_res["base_model"] = cor_res["model"].apply(read_base)
cor_res["ensemble_method"] = cor_res["model"].apply(read_ensemble)
Кроме того, посчитаем качество базовых моделей, входящих в каждый из ансамблей.
def base_model_prauc(ensemble, x, y):
qual = np.zeros(ensemble.n_estimators)
for ind, est in enumerate(ensemble.estimators_):
x_test = x.values[:, ensemble.estimators_features_[i]]
if not isinstance(est, sklearn.svm.SVC):
y_pred = est.predict_proba(x_test)[:, 1]
else:
y_pred = est.decision_function(x_test)
qual[ind] = average_precision_score(y_score=y_pred, y_true=y)
return qual
base_prauc = {}
for name, model in models.items():
if not "Bagging" in name and not "RSM" in name:
continue
base_prauc[name] = base_model_prauc(model, x_test, y_test)
base_prauc_res = pd.DataFrame(base_prauc)
base_prauc_res = base_prauc_res.melt(
value_vars=base_prauc_res.columns, value_name="pr_auc", var_name="model"
)
base_prauc_res["base_model"] = base_prauc_res["model"].apply(read_base)
base_prauc_res["ensemble_method"] = base_prauc_res["model"].apply(read_ensemble)
plt.figure(figsize=(16, 12))
plt.subplot(211)
sns.boxplot(data=cor_res, y="paircor", x="base_model", hue="ensemble_method")
plt.title("Pairwise correlations in ensembles", size=25)
plt.xlabel("", size=20)
plt.ylabel("Pairwise correlation", size=20)
plt.legend(fontsize=20, loc="lower left")
plt.tick_params(axis="both", which="major", labelsize=14)
plt.subplot(212)
sns.boxplot(data=base_prauc_res, y="pr_auc", x="base_model", hue="ensemble_method")
plt.title("Base model quality", size=25)
plt.xlabel("", size=20)
plt.ylabel("PR-AUC", size=20)
plt.subplots_adjust()
plt.legend(fontsize=20, loc="lower left")
plt.tick_params(axis="both", which="major", labelsize=14)
plt.show()
Можно сделать следующие выводы:
Из предыдущей части мы увидели, что использование bagging или RSM для SVM или подобных моделей не несет большого смысла. Но для деревьев решений это не так. Будем брать деревья большой глубины. Незначительные изменения в данных приводят к значительным изменениям в топологии таких деревьев. Таким образом, мы приходим к случайному лесу = Bagging + RSM над деревом решений.
При этом RSM в классическом случайном лесе делается не на уровне дерева, а на уровне узла. В каждом узле дерева, когда мы выбираем лучшее разбиение его на два дочерних, мы просматриваем не все признаки, а только определенное их количество.
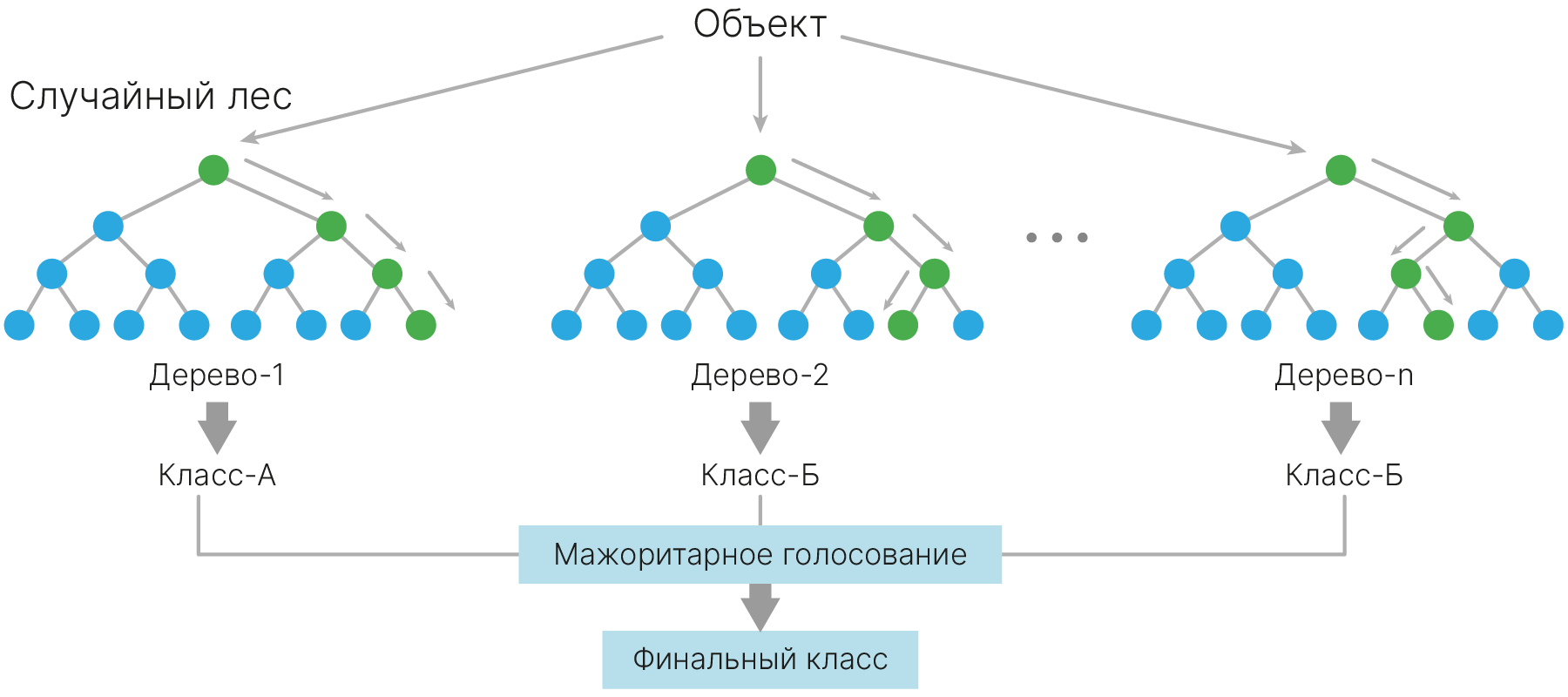
Случайный лес работает лучше, чем отдельное случайно взятое дерево. Но главное, что случайный лес намного более устойчив к шуму. Это свойство до сих пор позволяет случайному лесу успешно использоваться в областях с шумными данными.
Для случайного леса верно следующее: когда мы берем множество базовых классификаторов (в данном случае деревьев) и усредняем их, то результат этих усреднений стремится к идеальному дереву решений, причем построенному на идеальных, а не на исходных признаках.
Проверим это на задаче регрессии California Housing dataset 🛠️[doc].
calif_housing = sklearn.datasets.fetch_california_housing()
x = calif_housing.data
y = calif_housing.target
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
Данные — средние характеристики квартиры в доме. Цель — предсказать цену на дом.
Создадим несколько случайных лесов с различным количеством деревьев и простое дерево решений для сравнения с ним (baseline).
from sklearn.ensemble import RandomForestRegressor
from sklearn.tree import DecisionTreeRegressor
models_rf = {}
# add single decision tree for comparison
models_rf["DT"] = GridSearchCV(
DecisionTreeRegressor(),
{"max_depth": [1, 3, 5, 7, 10], "min_samples_leaf": [1, 3, 5, 10]},
)
# this can be done faster, see warm_start parameter for this
# (https://stackoverflow.com/questions/42757892/how-to-use-warm-start)
for n_estimators in [3, 5, 10, 50, 100, 150, 250]:
models_rf[f"RF{n_estimators}"] = RandomForestRegressor(
n_estimators=n_estimators, random_state=42, n_jobs=-1
) # run in parallel
Обучим все модели. Для этого напишем вспомогательную функцию, которая будет обучать переданные ей модели и считать для них качество на тесте.
from sklearn.metrics import mean_squared_error
def train_and_test_regressor(models, x_train, y_train, x_test, y_test, verb=True):
boot_scores = {}
for name, model in models.items():
model.fit(x_train, y_train) # train the model
y_pred = model.predict(x_test) # get predictions
boot_scores[name] = bootstrap_metric( # calculate bootstrap score
y_test,
y_pred,
metric_fn=lambda x, y: mean_squared_error(y_true=x, y_pred=y),
)
if verb:
print(f"Fitted {name} with bootstrap score {boot_scores[name].mean():.3f}")
results = pd.DataFrame(boot_scores)
return results
results_rf = train_and_test_regressor(models_rf, x_train, y_train, x_test, y_test)
Fitted DT with bootstrap score 0.395 Fitted RF3 with bootstrap score 0.338 Fitted RF5 with bootstrap score 0.302 Fitted RF10 with bootstrap score 0.277 Fitted RF50 with bootstrap score 0.257 Fitted RF100 with bootstrap score 0.254 Fitted RF150 with bootstrap score 0.252 Fitted RF250 with bootstrap score 0.252
plt.figure(figsize=(16, 6))
sns.boxplot(data=results_rf)
plt.ylabel("MSE", size=20)
plt.xlabel("n_estimators", size=20)
plt.title("Number of estimators vs MSE", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.show()
Увеличение числа базовых моделей сначала сильно улучшает качество модели. Однако после определенного количества базовых моделей улучшение качества становится незначительным.
Чем больше глубина дерева, тем большая нескорелированность базовых моделей будет получаться. В общем случае в случайном лесе важно использовать именно глубокие деревья, причем в большинстве случаев их глубину не надо ограничивать (или ограничивать большими значениями порядка 10–12).
Обучим случайный лес с заданной глубиной дерева и сравним с одиночным деревом такой же глубины.
dt_depth = {}
rf_depth = {}
for depth in range(1, 20, 2):
dt_depth[depth] = DecisionTreeRegressor(max_depth=depth, random_state=42)
rf_depth[depth] = RandomForestRegressor(
n_estimators=100, max_depth=depth, random_state=42, n_jobs=-1
) # run in parallel
dt_res = train_and_test_regressor(
dt_depth, x_train, y_train, x_test, y_test, verb=False
)
rf_res = train_and_test_regressor(
rf_depth, x_train, y_train, x_test, y_test, verb=False
)
dt_res = dt_res.melt(value_vars=dt_res.columns, value_name="mse", var_name="tree_depth")
dt_res["model"] = "DT"
rf_res = rf_res.melt(value_vars=rf_res.columns, value_name="mse", var_name="tree_depth")
rf_res["model"] = "RF"
depth_res = pd.concat((dt_res, rf_res))
plt.figure(figsize=(12, 8))
sns.boxplot(data=depth_res, x="tree_depth", y="mse", hue="model")
plt.xlabel("Tree depth", size=20)
plt.ylabel("MSE", size=20)
plt.title("Tree depth vs MSE", size=20)
plt.legend()
plt.tick_params(axis="both", which="major", labelsize=14)
plt.show()
Лучшие результаты показывает случайный лес из наиболее глубоких деревьев.
Качество случайного леса с малой глубиной дерева не отличается от качества одиночного дерева той же глубины. Это связано с тем, что деревья малой глубины слабо отличаются друг от друга (высокий bias и низкий variance), потому усреднение их предсказаний почти не улучшает качество.
Отметим, что в случае малых выборок ограничения на глубину дерева могут дать выигрыш.
Иногда качество случайного леса можно улучшить, если поставить небольшое ограничение на минимальное число объектов в листе, чтобы запретить явно переобученные деревья.
dt_models_min_samples = {}
rf_models_min_samples = {}
for mn_sm in [1, 3, 5, 7, 10]:
dt_models_min_samples[mn_sm] = DecisionTreeRegressor(
max_depth=None, min_samples_leaf=mn_sm, random_state=42
)
rf_models_min_samples[mn_sm] = RandomForestRegressor(
n_estimators=100,
max_depth=None,
min_samples_leaf=mn_sm,
random_state=42,
n_jobs=-1,
) # run in parallel
dt_results_mn_samples = train_and_test_regressor(
dt_models_min_samples, x_train, y_train, x_test, y_test
)
rf_results_mn_samples = train_and_test_regressor(
rf_models_min_samples, x_train, y_train, x_test, y_test
)
dt_results_mn_samples = dt_results_mn_samples.melt(
value_vars=dt_results_mn_samples.columns, value_name="mse", var_name="min_samples"
)
dt_results_mn_samples["model"] = "DT"
rf_results_mn_samples = rf_results_mn_samples.melt(
value_vars=rf_results_mn_samples.columns, value_name="mse", var_name="min_samples"
)
rf_results_mn_samples["model"] = "RF"
leaf_res = pd.concat((dt_results_mn_samples, rf_results_mn_samples))
Fitted 1 with bootstrap score 0.528 Fitted 3 with bootstrap score 0.446 Fitted 5 with bootstrap score 0.428 Fitted 7 with bootstrap score 0.405 Fitted 10 with bootstrap score 0.388 Fitted 1 with bootstrap score 0.254 Fitted 3 with bootstrap score 0.256 Fitted 5 with bootstrap score 0.260 Fitted 7 with bootstrap score 0.266 Fitted 10 with bootstrap score 0.274
plt.figure(figsize=(12, 8))
sns.boxplot(data=leaf_res, x="min_samples", y="mse", hue="model")
plt.xlabel("Tree depth", size=20)
plt.ylabel("MSE", size=20)
plt.title("Tree depth vs MSE", size=20)
plt.legend()
plt.tick_params(axis="both", which="major", labelsize=14)
plt.show()
В данном случае, однако, ограничение на количество объектов в листе ухудшает качество ансамбля. Одна из причин заключается в том, что с увеличением числа ограничений на дерево уменьшается непохожесть деревьев друг на друга, и качество случайного леса так же начинает уменьшаться.
Существует мнение, что случайный лес не переобучается. Это не так. Можно подобрать такие два набора параметров, что первый даст лучшее качество на тренировочной выборке, а второй — на тестовой. При этом увеличение числа деревьев в ансамбле с этим справиться поможет слабо.
Возьмем, к примеру, наш синтетический пример на плоскости.
from sklearn.ensemble import RandomForestClassifier
x, y = sklearn.datasets.make_moons(n_samples=500, noise=0.30, random_state=42)
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
plt.figure(figsize=(16, 6))
plt.subplot(121)
clf = DecisionTreeClassifier(max_depth=10, random_state=42)
clf.fit(x_train, y_train)
plot_decision_boundary(clf, x, y)
plt.title("Single Decision Tree", fontsize=14)
plt.subplot(122)
rf = RandomForestClassifier(n_estimators=1000)
rf.fit(x_train, y_train)
plot_decision_boundary(rf, x, y)
plt.title("Random forest", fontsize=14)
plt.show()
Видны области, в которых случайный лес переобучился.
Добавление ограничения на число объектов в листьях улучшает ситуацию.
plt.figure(figsize=(16, 6))
plt.subplot(121)
rf1 = RandomForestClassifier(n_estimators=1000)
rf1.fit(x_train, y_train)
plot_decision_boundary(rf1, x, y)
plt.title("Random forest", fontsize=14)
plt.subplot(122)
rf2 = RandomForestClassifier(n_estimators=1000, min_samples_leaf=5)
rf2.fit(x_train, y_train)
plot_decision_boundary(rf2, x, y)
plt.title("Random forest, min_samples_leaf=5", fontsize=14)
plt.show()
Лес без ограничения на минимальное число объектов в листе переобучился — достиг максимального качества на обучающей выборке, но на тестовой имеет качество ниже, чем лес с ограничением.
y_score = rf1.predict(x_train)
q = average_precision_score(y_true=y_train, y_score=y_score)
print(f"RF1 Train: {q:.02}")
y_score = rf1.predict(x_test)
q = average_precision_score(y_true=y_test, y_score=y_score)
print(f"RF1 Test: {q:.02}")
y_score = rf2.predict(x_train)
q = average_precision_score(y_true=y_train, y_score=y_score)
print(f"RF2 Train: {q:.02}")
y_score = rf2.predict(x_test)
q = average_precision_score(y_true=y_test, y_score=y_score)
print(f"RF2 Test: {q:.02}")
RF1 Train: 1.0 RF1 Test: 0.87 RF2 Train: 0.91 RF2 Test: 0.91
Благодаря механизму обучения случайного леса у нас появляется еще один способ валидировать модель. Для каждого дерева используются не все объекты нашей выборки, следовательно мы можем получать предсказания деревьев на объектах, которые не использовались для обучения этих деревьев.
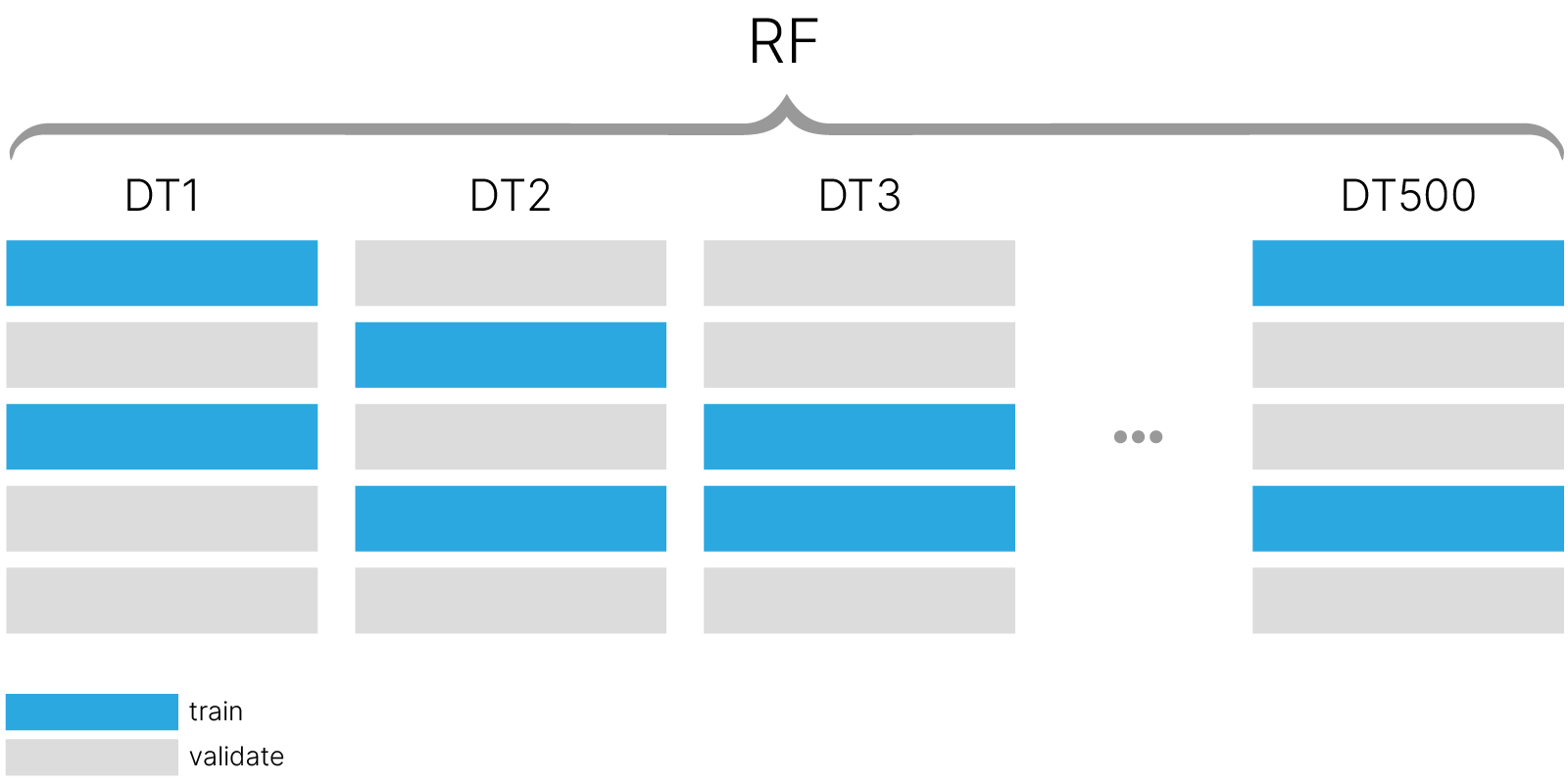
За это отвечает параметр oob_score (по умолчанию False)
from sklearn.model_selection import cross_validate
rf_oob = RandomForestClassifier(n_estimators=1000, min_samples_leaf=5, oob_score=True)
rf_oob.fit(x, y)
print(f"RF OOB score: {rf_oob.oob_score_:.02}")
scores = cross_validate(rf_oob, x, y, cv=5)
print(f"RF CV score: {scores['test_score'].mean():.02}")
rf_oob.fit(x_train, y_train)
print(f"RF Test set score: {rf_oob.score(x_test, y_test):.02}")
RF OOB score: 0.92 RF CV score: 0.91 RF Test set score: 0.92
Важно понимать, что OOB score не заменяет другие способы валидации, а является дополнительным способом, который используется в основном тогда, когда данных мало.
Случайный лес — инструмент для уменьшения variance нашей модели. Можно показать, что при стремлении числа моделей в ансамбле к бесконечности, а их коррелированности — к 0, variance ансамбля стремится к нулю. Однако при этом bias ансамбля будет равен bias базовой модели.
Продемонстрируем это:
plt.figure(figsize=(16, 8))
# Decision trees
for i, max_depth in enumerate([1, 3, 5, 12]):
plt.subplot(241 + i)
dt = DecisionTreeClassifier(max_depth=max_depth)
dt.fit(x_train, y_train)
plot_decision_boundary(dt, x, y, alpha=0.5, bolded=True)
plt.xticks([], [])
plt.yticks([], [])
plt.title(f"Decision tree, max_depth={max_depth}", fontsize=14)
plt.xlabel("")
plt.ylabel("")
plt.xticks([], [])
plt.yticks([], [])
# Random forests
for i, max_depth in enumerate([1, 3, 5, 12]):
plt.subplot(245 + i)
rf = RandomForestClassifier(max_depth=max_depth, n_estimators=500, n_jobs=-1)
rf.fit(x_train, y_train)
plot_decision_boundary(rf, x, y, alpha=0.5, bolded=True)
plt.title(f"Random forest, max_depth={max_depth}", fontsize=14)
plt.xlabel("")
plt.ylabel("")
plt.xticks([], [])
plt.yticks([], [])
Видим, что общая сложность решающей границы меняется не сильно: bias случайного леса по сравнению с bias дерева решений не меняется. А вот гладкость границы увеличивается, тем самым, уменьшается variance
Бустинг — это еще один способ ансамблирования моделей. В отличие от случайного леса, где каждая модель в ансамбле строится независимо, в бустинге построение очередной модели зависит от уже состоящих в ансамбле моделей. Каждая следующая модель в ансамбле стремится улучшить предсказание всего ансамбля.
Бустинг позволяет нам на основе большого числа "слабых" моделей получить одну "сильную". Под слабыми моделями подразумеваем модели, точность которых может быть лишь немногим выше случайного угадывания.
В качестве моделей традиционно используются деревья решений, но не большой глубины, а наоборот — маленькой, чтобы каждое из них не могло выучить выборку хорошо.

Из всех бустингов больше всего прославился и доказал свою эффективность градиентный бустинг. Он позволяет получить решение, которое сложно побить другими видами моделей.
Начнем с интуиции. Предположим, что мы играем в гольф. Наша задача — загнать мячик в лунку, причем, когда мячик далеко от нее, мы можем ударить посильнее, чтобы сократить расстояние, но когда мы уже близко к лунке, то стараемся бить клюшкой аккуратнее, чтобы не промахнуться. После каждого удара мы оцениваем расстояние до лунки и приближаем мячик в ее сторону. Применительно к нашей теме удар клюшкой по мячику — это каждая модель в градиентном бустинге.

Цель $i$-той модели в ансамбле — скорректировать ошибки предыдущих ${i-1}$ моделей. В результате, когда мы суммируем вклады всех моделей ансамбля, получается хорошее предсказание.
Давайте формализуем, что нам нужно, чтобы обучить алгоритм градиентного бустинга:
Минимизировать ошибку будем с помощью градиентного спуска.
Рзаберем пошагово:
Начинаем с первого предсказания, можем выбрать на самом деле любое число, например среднее значение
$$ \large \hat{f}(x)=\hat{f}_0, \hat{f}_0=\gamma, \gamma \in \mathbb{R} \tag{1}$$Либо подобрать с наименьшей ошибкой
$$\large \hat{f}_0=\underset{\gamma}{\arg \min } \sum_{i=1}^n L\left(y_i, \gamma\right) $$Посмотрим на графике, как бы могла выглядеть наша зависимость. Посчитаем ошибку и отобразим наше предсказание.
В нашем примере мы видим, что нужно двигаться вправо, чтобы уменьшить ошибку. В действительности мы этого не знаем, но можем посчитать градиент и узнать направление возрастания функции ошибки. Нас же интересует обратное направление или градиент со знаком минус (антиградиент).
$$\large r_{i t}=-\frac{\partial L\left(y_i, f\left(x_i\right)\right)}{\partial f\left(x_i\right)} \quad \tag{2}$$
Строим новый базовый алгоритм $h_t(x)$, который обучается на то, чтобы уменьшить ошибку от текущего состояния ансамбля, и в качестве целевой переменной для него берем антиградиент функции потерь $\left\{\left(x_i, r_{i t}\right)\right\}_{i=1, \ldots, n}$
$$\large\underset{\theta}{\arg \min } \sum_{i=1}^n L\left(h(x_i, \theta), r_{it}\right) \tag{3}$$Подбираем оптимальный параметр $\large \rho$. Этот параметр будет разным у каждого дерева в нашем ансамбле, в отличие от learning rate:
$$\large \rho_t=\underset{\rho}{\arg \min } \sum_{i=1}^n L\left(y_i, \hat{f}\left(x_i\right)+\rho \cdot h\left(x_i, \theta\right)\right) \tag{4}$$
Сдвигаем предсказание в сторону уменьшения ошибки, где $\lambda$ — это learning rate:
$$\large \hat{f}_t(x)= \lambda \cdot \rho_t \cdot h_t(x) \tag{5}$$
Обновляем текущее приближение $\hat{f}(x)$: $$ \large \hat{f}(x) \leftarrow \hat{f}(x)+\hat{f}_t(x)=\sum_{i=0}^t \hat{f}_i(x) \tag{6} $$
Далее повторяем шаги 2–6, пока не получим требуемое качество, и собираем итоговый ансамбль $\hat{f}(x)$:
$$ \large \hat{f}(x)=\sum_{i=0}^M \hat{f}_i(x) $$Когда мы говорили про базовые модели, то предполагали, что этими базовыми моделями являются деревья решений. Однако это необязательно, можно использовать и другие алгоритмы в качестве базовых моделей.
Деревья решений имеют ряд преимуществ:
Гибкость — деревья решений могут описывать сложные нелинейные взаимосвязи между объектами и целевой переменной. Они могут обрабатывать как числовые, так и категориальные данные и работать с пропущенными значениями.
Интерпретируемость — деревья решений просты в понимании и интерпретации. Они дают четкое представление о том, как модель пришла к определенному прогнозу.
Устойчивость к выбросам — деревья решений менее чувствительны к выбросам, чем другие алгоритмы машинного обучения. Они способны изолировать их и предотвратить их влияние на всю модель.
Эффективность — деревья решений могут быть построены быстро, они способны обрабатывать большие наборы данных.
Например, запустим градиентный бустинг без подбирания параметров:
calif_housing = sklearn.datasets.fetch_california_housing()
x = calif_housing.data
y = calif_housing.target
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
И напишем функцию, которая будет автоматически обучать переданные ей модели и считать для них качество на тесте, чтобы избавиться от необходимости копировать код между ячейками:
from sklearn.metrics import mean_squared_error
def train_and_test_regressor(models, x_train, y_train, x_test, y_test):
for name, model in models.items():
print(f"Fitting {name}")
model.fit(x_train, y_train)
predictions = {}
for name, model in models.items():
y_pred = model.predict(x_test)
predictions[name] = y_pred
boot_scores = {}
for name, y_pred in predictions.items():
print(f"Calculating bootstrap score for {name}")
boot_score = bootstrap_metric(
y_test,
y_pred,
metric_fn=lambda x, y: mean_squared_error(y_true=x, y_pred=y),
)
boot_scores[name] = boot_score
results = pd.DataFrame(boot_scores)
# cast to long format
results = results.melt(
value_vars=results.columns, value_name="mse", var_name="model"
)
return results
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
models = {}
# make pipeline for normalization
models["LinReg"] = make_pipeline(StandardScaler(with_mean=False), LinearRegression())
models["RF"] = RandomForestRegressor(
n_estimators=250, # for better result set to 1000
max_depth=None,
min_samples_leaf=1,
n_jobs=-1,
random_state=42,
)
models["GradientBoosting"] = GradientBoostingRegressor(
learning_rate=0.1, # for better result set to 0.05
n_estimators=250, # for better result set to 1000
random_state=42,
)
results_boost = train_and_test_regressor(models, x_train, y_train, x_test, y_test)
Fitting LinReg Fitting RF Fitting GradientBoosting Calculating bootstrap score for LinReg Calculating bootstrap score for RF Calculating bootstrap score for GradientBoosting
plt.figure(figsize=(12, 4))
ax = sns.boxplot(data=results_boost, y="mse", x="model", hue="model")
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("LR vs RF vs GB", size=25)
plt.xticks(size=20)
plt.show()
Видим, что бустинг сразу дает хороший результат.
В то же время Gradient boosting, в отличие от случайного леса, может сильно переобучиться. Это важно понимать. Для небольших датасетов часто может оказаться, что случайный лес дает более надежные результаты.
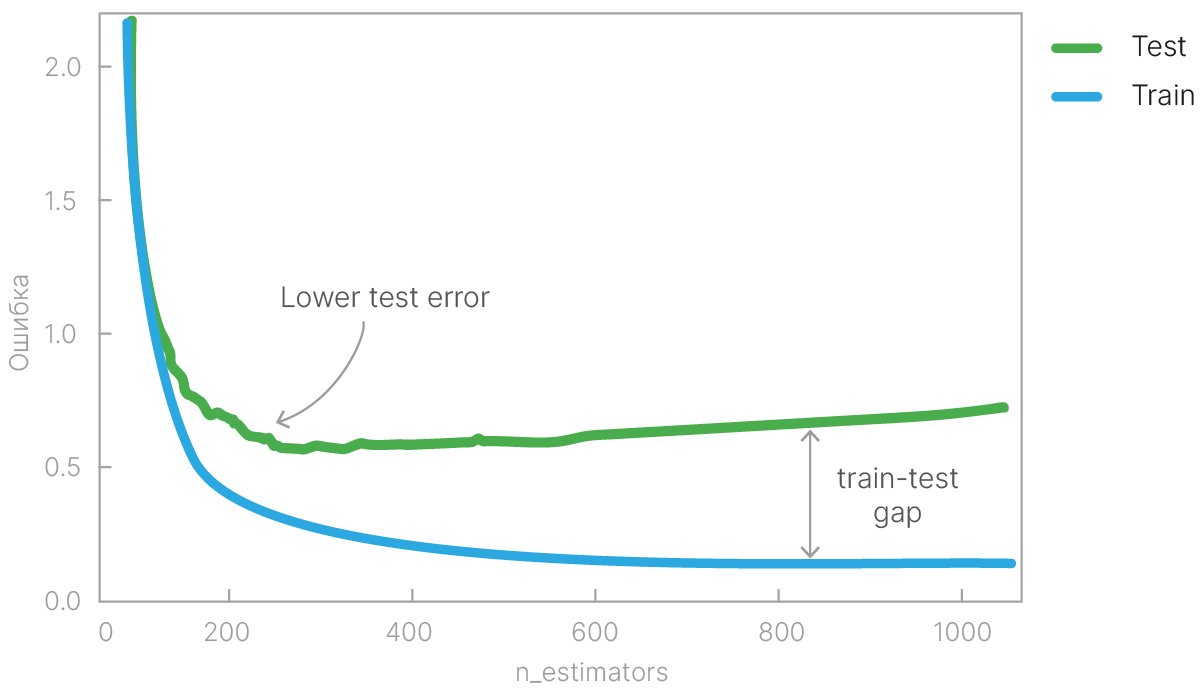
gbtree = GradientBoostingRegressor(
n_estimators=300, learning_rate=1.0 # faster learning rate to force ovefitting
)
gbtree.fit(x_train, y_train)
GradientBoostingRegressor(learning_rate=1.0, n_estimators=300)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
GradientBoostingRegressor(learning_rate=1.0, n_estimators=300)
Используем метод staged_predict, который есть во многих реализациях бустинга в том или ином виде. Он получает предсказание от первых $i$ деревьев ансамбля, что позволяет быстро строить график качества градиентного бустинга в зависимости от числа базовых моделей:
error_train = []
error_test = []
for it, (y_train_pred, y_test_pred) in enumerate(
zip(gbtree.staged_predict(x_train), gbtree.staged_predict(x_test))
):
ertr = mean_squared_error(y_true=y_train, y_pred=y_train_pred)
error_train.append(ertr)
erte = mean_squared_error(y_true=y_test, y_pred=y_test_pred)
error_test.append(erte)
plt.figure(figsize=(10, 5))
plt.plot(error_train, label="train", c="#2DA9E1", linewidth=4)
plt.plot(error_test, label="test", c="#4AAE4D", linewidth=4)
plt.xlabel("n_estimators", size=20)
plt.ylabel("mse", size=20)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.legend(fontsize=20)
plt.show()
Здесь мы немного схитрили, сильно увеличив learning rate нашей модели — дополнительный множитель к весу, с которым добавляются в нее новые модели. Из-за этого даже на таком простом датасете мы в состоянии увидеть явное переобучение.
Давайте об этом learning rate и поговорим.
Как у градиентного спуска есть learning rate, который определяет силу каждого нашего следующего шага, так и у градиентного бустинга есть параметр, который называется shrinkage или learning rate — это дополнительный параметр, на который мы домножаем вес, с которым мы добавляем новые модели в ансамбль.
Мы не хотим сильно скакать по пространству решений, мы хотим спускаться медленно и сойтись к какому-то хорошему минимуму. Потому мы вес каждой модели, которую мы рассчитываем по специальному алгоритму, еще домножаем на маленький коэффициент, который называется shrinkage или learning rate. Фактически, мы берем и умножаем градиент на некий $\alpha$ (это то же, что было в градиентном спуске, ничего нового мы не добавили).
Если не домножать вес каждой модели дополнительно на этот параметр, то мы можем попасть в ситуацию, когда будем пролетать мимо минимума функции ошибки (та же опасность, что и в обычном градиентном спуске).
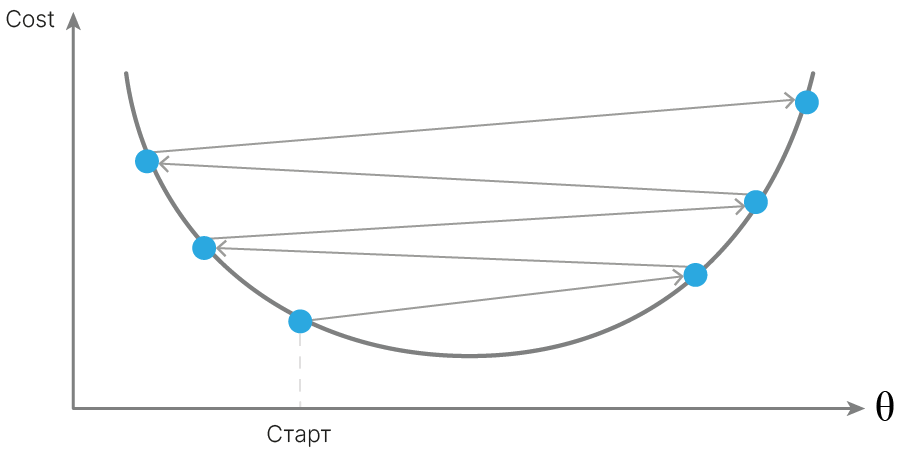
Как и в случае с градиентным спуском, learning rate влияет не только на то, как быстро мы станем переобучаться, но и на глубину минимума, который мы найдем.
# here anb below in the cell can be set to 1000 for better visualization
gbtrees_list = []
for lr in [1, 0.5, 0.1, 0.05, 0.01]:
gbtree = GradientBoostingRegressor(n_estimators=500, learning_rate=lr)
gbtree.fit(x_train, y_train)
gbtrees_list.append(gbtree)
lr = []
step = []
mse = []
for gb_tree in gbtrees_list:
for it, y_test_pred in enumerate(gb_tree.staged_predict(x_test)):
erte = mean_squared_error(y_true=y_test, y_pred=y_test_pred)
mse.append(erte)
lr.append(str(gb_tree.learning_rate))
step.append(it)
df = pd.DataFrame({"learning_rate": lr, "n_estimators": step, "mse": mse})
plt.figure(figsize=(16, 6))
sns.lineplot(data=df, x="n_estimators", y="mse", hue="learning_rate", lw=3)
plt.xlabel("n_estimators", size=20)
plt.ylabel("mse", size=20)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.ylim((0.2, 0.6))
plt.legend(fontsize=20)
plt.show()
В данном случае мы видим, что значение learning rate, установленное по умолчанию (learning_rate=0.1), позволяет получить наименьшую ошибку на валидации.
Слишком большие значения learning rate (1 и 0.5) приводят к тому, что мы не достигаем таких глубоких минимумов и начинаем переобучаться.
Слишком малое значение learning rate может привести к тому, что нам понадобится очень большое число деревьев, чтобы достигнуть минимума (если мы его вообще достигнем).
Число деревьев, как было видно из предыдущего графика, зависит от установленного learning rate.
Потому обычно ставят learning_rate = 0.1 и подбирают оптимальное значение числа деревьев в ансамбле.
Делают это на кросс-валидации, но для экономии времени просто дополнительно разобьем train датасет:
x_learn, x_valid, y_learn, y_valid = train_test_split(x_train, y_train, random_state=42)
gbtree = GradientBoostingRegressor(n_estimators=1000, learning_rate=0.1)
gbtree.fit(x_learn, y_learn)
error_train = []
error_test = []
for it, (y_learn_pred, y_valid_pred) in enumerate(
zip(gbtree.staged_predict(x_learn), gbtree.staged_predict(x_valid))
):
ertr = mean_squared_error(y_true=y_learn, y_pred=y_learn_pred)
error_train.append(ertr)
erte = mean_squared_error(y_true=y_valid, y_pred=y_valid_pred)
error_test.append(erte)
plt.figure(figsize=(10, 5))
plt.plot(error_train, label="train", c="#2DA9E1", linewidth=4)
plt.plot(error_test, label="test", c="#4AAE4D", linewidth=4)
plt.xlabel("n_estimators", size=20)
plt.ylabel("mse", size=20)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.legend(fontsize=20)
plt.show()
Видим, что ошибка продолжает медленно уменьшаться, но увеличение идет очень маленькое, потому в целях демонстрации выберем число деревьев равным 500.
В случае бустинга нам нужны слабые модели. Поэтому очень глубокие деревья в бустинге встречаются редко — бустинг с ними проиграет по качеству.
Обычно глубина дерева выбирается вместе с минимальным числом объектов в листе min_samples_leaf или весом листа min_weight_fraction_leaf, так как эти параметры взаимосвязаны и вместе влияют на сложность полученных деревьев.
Здесь же в целях демонстрации мы подберем сначала глубину дерева, а потом минимальное число объектов.
models = {}
for depth in (1, 2, 3, 5, 10):
models[depth] = GradientBoostingRegressor(
n_estimators=500, learning_rate=0.1, max_depth=depth, random_state=42
)
depth_boost = train_and_test_regressor(models, x_learn, y_learn, x_valid, y_valid)
Fitting 1 Fitting 2 Fitting 3 Fitting 5 Fitting 10 Calculating bootstrap score for 1 Calculating bootstrap score for 2 Calculating bootstrap score for 3 Calculating bootstrap score for 5 Calculating bootstrap score for 10
plt.figure(figsize=(16, 6))
sns.boxplot(data=depth_boost, y="mse", x="model", hue="model", palette="tab10")
plt.xlabel("GB depth", size=20)
plt.ylabel("MSE", size=20)
plt.title("GB depth vs MSE", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.legend([], [], frameon=False)
plt.show()
Искомая глубина находится между 3 и 10. Добавим на график точки 4, 6 и 7.
models_add = {}
for depth in (4, 6, 7):
models_add[depth] = GradientBoostingRegressor(
n_estimators=500, learning_rate=0.1, max_depth=depth, random_state=42
)
depth_boost_add = train_and_test_regressor(
models_add, x_learn, y_learn, x_valid, y_valid
)
Fitting 4 Fitting 6 Fitting 7 Calculating bootstrap score for 4 Calculating bootstrap score for 6 Calculating bootstrap score for 7
depth_boost_joined = pd.concat([depth_boost, depth_boost_add])
plt.figure(figsize=(16, 6))
sns.boxplot(
data=depth_boost_joined,
y="mse",
x="model",
order=[1, 2, 3, 4, 5, 6, 7, 10],
hue="model",
palette="tab10",
)
plt.xlabel("GB depth", size=20)
plt.ylabel("MSE", size=20)
plt.title("GB depth vs MSE", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.legend([], [], frameon=False)
plt.show()
Значит, оптимальная для данной задачи глубина — 5.
Этот параметр влияет на сложность полученных деревьев. Как уже отмечалось ранее, стоит подбирать его вместе с глубиной, но мы ограничены по времени.
models = {}
for min_samples_leaf in (1, 3, 5, 7, 9, 11):
models[min_samples_leaf] = GradientBoostingRegressor(
n_estimators=500,
learning_rate=0.1,
max_depth=5,
min_samples_leaf=min_samples_leaf,
random_state=42,
)
mns_boost = train_and_test_regressor(models, x_learn, y_learn, x_valid, y_valid)
Fitting 1 Fitting 3 Fitting 5 Fitting 7 Fitting 9 Fitting 11 Calculating bootstrap score for 1 Calculating bootstrap score for 3 Calculating bootstrap score for 5 Calculating bootstrap score for 7 Calculating bootstrap score for 9 Calculating bootstrap score for 11
plt.figure(figsize=(16, 6))
sns.boxplot(data=mns_boost, y="mse", x="model", hue="model", palette="tab10")
plt.xlabel("Min samples in leaf", size=20)
plt.ylabel("MSE", size=20)
plt.title("GB min samples leaf vs MSE", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.legend([], [], frameon=False)
plt.show()
Поставим число объектов в листе, равное 9.
Можно каждому дереву в ансамбле давать только часть объектов из выборки — получим стохастический градиентный бустинг. За это отвечает параметр subsample.
Аналогично можно давать каждому дереву в ансамбле лишь часть признаков — max_features.
Это может давать дополнительный прирост качества. Сейчас мы этот этап опускаем, так как у нас мало признаков и не очень много объектов, а также в целях экономии времени.
После того, как мы подобрали остальные параметры, можно попытаться выиграть дополнительное качество за счет понижения learning_rate и одновременного увеличения числа деревьев в ансамбле.
Построим график качества для текущего learning_rate — мы же брали не оптимальное число предсказателей. Посмотрим, можно ли уже на финальном этапе взять побольше.
gbtree = GradientBoostingRegressor(
n_estimators=1000,
max_depth=5,
min_samples_leaf=9,
learning_rate=0.1,
random_state=42,
)
gbtree.fit(x_learn, y_learn)
error_train = []
error_test = []
for it, (y_learn_pred, y_valid_pred) in enumerate(
zip(gbtree.staged_predict(x_learn), gbtree.staged_predict(x_valid))
):
ertr = mean_squared_error(y_true=y_learn, y_pred=y_learn_pred)
error_train.append(ertr)
erte = mean_squared_error(y_true=y_valid, y_pred=y_valid_pred)
error_test.append(erte)
plt.figure(figsize=(10, 5))
plt.plot(error_train, label="train", c="#2DA9E1", linewidth=4)
plt.plot(error_test, label="test", c="#4AAE4D", linewidth=4)
plt.xlabel("n_estimators", size=20)
plt.ylabel("mse", size=20)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.legend(fontsize=20)
plt.show()
Возьмем 500 деревьев.
models = {}
models["LinReg"] = make_pipeline(StandardScaler(with_mean=False), LinearRegression())
models["RF"] = RandomForestRegressor(
n_estimators=250, max_depth=None, min_samples_leaf=1, n_jobs=-1, random_state=42
)
models["GBR"] = GradientBoostingRegressor(
learning_rate=0.1, n_estimators=250, random_state=42
)
models["GBR tuned"] = GradientBoostingRegressor(
learning_rate=0.1,
n_estimators=500,
max_depth=5,
min_samples_leaf=9,
random_state=42,
)
tuned_boost = train_and_test_regressor(models, x_train, y_train, x_test, y_test)
Fitting LinReg Fitting RF Fitting GBR Fitting GBR tuned Calculating bootstrap score for LinReg Calculating bootstrap score for RF Calculating bootstrap score for GBR Calculating bootstrap score for GBR tuned
plt.figure(figsize=(16, 6))
sns.boxplot(data=tuned_boost, y="mse", x="model", hue="model")
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("Boosting and others", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(fontsize=20)
plt.show()
Видим, что мы дополнительно уменьшили ошибку.
В то время как случайный лес уменьшал только variance модели, бустинг стремится уменьшить и bias, и variance.
from sklearn.ensemble import GradientBoostingClassifier
x, y = sklearn.datasets.make_moons(n_samples=500, noise=0.30, random_state=42)
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
plt.figure(figsize=(16, 12))
# Decision trees
for i, max_depth in enumerate([1, 3, 5, 12]):
plt.subplot(3, 4, 1 + i)
dt = DecisionTreeClassifier(max_depth=max_depth)
dt.fit(x_train, y_train)
plot_decision_boundary(dt, x, y, alpha=0.4, bolded=True)
plt.xticks([], [])
plt.yticks([], [])
plt.title(f"Decision tree, max_depth={max_depth}", fontsize=13)
plt.xlabel("")
plt.ylabel("")
# Random forests
for i, max_depth in enumerate([1, 3, 5, 12]):
plt.subplot(3, 4, 5 + i)
rf = RandomForestClassifier(max_depth=max_depth, n_estimators=500, n_jobs=-1)
rf.fit(x_train, y_train)
plot_decision_boundary(rf, x, y, alpha=0.4, bolded=True)
plt.title(f"Random forest, max_depth={max_depth}", fontsize=13)
plt.xlabel("")
plt.ylabel("")
plt.xticks([], [])
plt.yticks([], [])
# Gradient boostings
for i, max_depth in enumerate([1, 3, 5, 12]):
plt.subplot(3, 4, 9 + i)
boost = GradientBoostingClassifier(max_depth=max_depth, n_estimators=250)
boost.fit(x_train, y_train)
plot_decision_boundary(boost, x, y, alpha=0.4, bolded=True)
plt.title(f"Gradient boosting, max_depth={max_depth}", fontsize=13)
plt.xlabel("")
plt.ylabel("")
plt.xticks([], [])
plt.yticks([], [])
Есть много модификаций градиентного бустинга. В отличие от реализации в sklearn, большая часть из них умеет параллелиться на CPU или даже на GPU.
Поэтому при работе с реальными данными использовать градиентный бустинг из sklearn не стоит. XGBoost и/или LigthGBM дадут результат как правило лучше и быстрее.
Мы хотим спускаться медленно и не хотим, чтобы модели по пути были сложными. Пусть минимально отличающимися от случайных, но при этом не очень сложными.
Поэтому XGBoost вводит специальный штраф за сложные деревья (большей глубины, чем 2–3). За счет того, что в градиентном бустинге можно минимизировать любую дифференцируемую функцию ошибок, мы просто добавляем штраф напрямую в функцию ошибок исходного градиентного бустинга.

calif_housing = sklearn.datasets.fetch_california_housing()
x = calif_housing.data
y = calif_housing.target
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
Скопируем параметры, которые совпадают в градиентном бустинге и XGBoost. Посмотрим, получится ли еще улучшить качество.
import xgboost
models_add = {}
models_add["xgb"] = xgboost.XGBRegressor(
n_estimators=500,
learning_rate=0.1,
max_depth=5,
random_state=42,
min_child_weight=9, # not exact analogue for min_samples_leaf
n_jobs=-1, # can be constructed in parrallel, much!!! faster)
objective="reg:squarederror",
)
xgb_add = train_and_test_regressor(models_add, x_train, y_train, x_test, y_test)
Fitting xgb Calculating bootstrap score for xgb
plt.figure(figsize=(16, 6))
sns.boxplot(data=pd.concat([tuned_boost, xgb_add]), y="mse", x="model", hue="model")
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("Boosting and others", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
Пусть и незначительно, но XGBoost лучше GBR. И, главное, в разы быстрее.
XGBoost немного иначе определяет важность листа: не сколько именно объектов попало в лист, а насколько объекты в листе имеют сильно разные предсказания. Из-за этого способа определения min_child_weight может принимать нецелые значения, в том числе меньше 1 (к примеру, в случае задачи классификации).
Попробуем подобрать только этот параметр. Заметьте, мы можем спокойно использовать 2000 деревьев, не боясь ждать результата расчетов долгое время.
models = {}
for min_child_weight in (1, 2, 3, 5, 7, 9, 11, 13, 15):
models[f"xGB_mnw{min_child_weight}"] = xgboost.XGBRegressor(
n_estimators=2000,
learning_rate=0.1,
max_depth=5,
random_state=42,
min_child_weight=min_child_weight,
n_jobs=-1,
objective="reg:squarederror",
)
xgb_mw = train_and_test_regressor(models, x_train, y_train, x_test, y_test)
Fitting xGB_mnw1 Fitting xGB_mnw2 Fitting xGB_mnw3 Fitting xGB_mnw5 Fitting xGB_mnw7 Fitting xGB_mnw9 Fitting xGB_mnw11 Fitting xGB_mnw13 Fitting xGB_mnw15 Calculating bootstrap score for xGB_mnw1 Calculating bootstrap score for xGB_mnw2 Calculating bootstrap score for xGB_mnw3 Calculating bootstrap score for xGB_mnw5 Calculating bootstrap score for xGB_mnw7 Calculating bootstrap score for xGB_mnw9 Calculating bootstrap score for xGB_mnw11 Calculating bootstrap score for xGB_mnw13 Calculating bootstrap score for xGB_mnw15
plt.figure(figsize=(16, 6))
ax = sns.boxplot(data=xgb_mw, y="mse", x="model", hue="model")
plt.setp(ax.get_xticklabels(), rotation=45)
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("XGB min_child_weight", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
Возьмем 9:
models_add2 = {}
models_add2["xgb_mcw"] = xgboost.XGBRegressor(
n_estimators=2000,
learning_rate=0.1,
max_depth=5,
random_state=42,
min_child_weight=9,
n_jobs=-1,
objective="reg:squarederror",
)
xgb_add2 = train_and_test_regressor(models_add2, x_train, y_train, x_test, y_test)
Fitting xgb_mcw Calculating bootstrap score for xgb_mcw
plt.figure(figsize=(16, 6))
sns.boxplot(
data=pd.concat([tuned_boost, xgb_add, xgb_add2]), y="mse", x="model", hue="model"
)
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("Boosting and others", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
Почти ничего не изменилось.
Он был изначально разработан для того, чтобы работать очень быстро. В него добавили много ухищрений, связанных с этим. Кроме этого, LightGBM по умолчанию строит дерево немного иначе, нежели XGBoost.
XGBoost по умолчанию строит дерево по уровням — на каждом уровне если узел можно разбить так, чтобы улучшить значение функции ошибки, то мы это делаем. Ограничены мы только максимальной глубиной дерева.
LightGBM же строит дерево по узлам. На каждом шаге бьется тот узел, разбиение которого сильнее всего минимизирует функцию ошибки. И ограничения на глубину нет. В LightGBM вводится ограничение не на глубину дерева, а на общее число листьев в итоговом дереве.

По умолчанию он еще быстрее (хотя в XGBoost тоже есть опции для ускорения).
Из-за особенностей построения им деревьев надо задавать не высоту дерева, а максимальное число листьев. Поставим пока так, чтобы число листьев было равно числу листьев в дереве высоты 6.
import lightgbm
models_add3 = {}
models_add3["lightgbm"] = lightgbm.LGBMRegressor(
n_estimators=2000, # can use more estimators due to SPEEEEEED
learning_rate=0.1,
max_depth=-1,
num_leaves=2**5,
random_state=42,
min_child_weight=9,
n_jobs=-1,
force_col_wise=True,
verbose=-1,
)
lgb_add = train_and_test_regressor(models_add3, x_train, y_train, x_test, y_test)
Fitting lightgbm Calculating bootstrap score for lightgbm
plt.figure(figsize=(16, 6))
sns.boxplot(
data=pd.concat([tuned_boost, xgb_add, xgb_add2, lgb_add]),
y="mse",
x="model",
hue="model",
)
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("Boosting and others", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
На уровне с XGBoost. Зато быстрее.
Отдельно подберем ограничение на число листьев. По словам создателей, оно не должно быть больше числа листьев в соответствующем дереве глубины 5, то есть 32.
models = {}
for num_leaves in (8, 16, 24, 32, 40):
models[f"LGB_lvn{num_leaves}"] = lightgbm.LGBMRegressor(
n_estimators=2000,
learning_rate=0.1,
max_depth=-1,
num_leaves=num_leaves,
random_state=42,
min_child_weight=10,
n_jobs=-1,
force_col_wise=True,
verbose=-1,
)
lgb_nl = train_and_test_regressor(models, x_learn, y_learn, x_valid, y_valid)
Fitting LGB_lvn8 Fitting LGB_lvn16 Fitting LGB_lvn24 Fitting LGB_lvn32 Fitting LGB_lvn40 Calculating bootstrap score for LGB_lvn8 Calculating bootstrap score for LGB_lvn16 Calculating bootstrap score for LGB_lvn24 Calculating bootstrap score for LGB_lvn32 Calculating bootstrap score for LGB_lvn40
plt.figure(figsize=(16, 6))
ax = sns.boxplot(data=lgb_nl, y="mse", x="model", hue="model")
plt.setp(ax.get_xticklabels(), rotation=45)
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("LGB num_leaves", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
Из этого графика можно сделать вывод, что оптимальное число листьев находится в районе 8.
models = {}
for num_leaves in (8, 12, 16, 20):
models[f"LGB_nl{num_leaves}"] = lightgbm.LGBMRegressor(
n_estimators=2000,
learning_rate=0.1,
max_depth=-1,
num_leaves=num_leaves,
random_state=42,
min_child_weight=10,
n_jobs=-1,
force_col_wise=True,
verbose=-1,
)
lgb_nl = train_and_test_regressor(models, x_learn, y_learn, x_valid, y_valid)
Fitting LGB_nl8 Fitting LGB_nl12 Fitting LGB_nl16 Fitting LGB_nl20 Calculating bootstrap score for LGB_nl8 Calculating bootstrap score for LGB_nl12 Calculating bootstrap score for LGB_nl16 Calculating bootstrap score for LGB_nl20
plt.figure(figsize=(16, 6))
sns.boxplot(data=lgb_nl, y="mse", x="model", hue="model")
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("LGB num_leaves", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
Выберем 12 листьев:
models_add4 = {}
models_add4["lightgbm lv12"] = lightgbm.LGBMRegressor(
n_estimators=2000,
learning_rate=0.1,
max_depth=-1,
num_leaves=12,
random_state=42,
min_child_weight=9,
n_jobs=-1,
force_col_wise=True,
verbose=-1,
)
lgb_add2 = train_and_test_regressor(models_add4, x_train, y_train, x_test, y_test)
Fitting lightgbm lv12 Calculating bootstrap score for lightgbm lv12
plt.figure(figsize=(16, 6))
sns.boxplot(
data=pd.concat([tuned_boost, xgb_add, xgb_add2, lgb_add, lgb_add2]),
y="mse",
x="model",
hue="model",
)
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("Boosting and others", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
Качество почти не изменилось.
Разработал Яндекс.
CatBoost:
!pip install -q catboost
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 98.5/98.5 MB 5.8 MB/s eta 0:00:00
import catboost
models_add4 = {}
models_add4["catboost"] = catboost.CatBoostRegressor(
iterations=2000,
learning_rate=0.1,
random_state=42,
verbose=0,
)
# task_type="GPU") # can use gpu, but no parallel-cpu option
cat_add = train_and_test_regressor(models_add4, x_train, y_train, x_test, y_test)
Fitting catboost Calculating bootstrap score for catboost
plt.figure(figsize=(16, 6))
sns.boxplot(
data=pd.concat([tuned_boost, xgb_add, xgb_add2, lgb_add, cat_add]),
y="mse",
x="model",
hue="model",
)
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("Boosting and others", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
Стало лучше.
Для оптимизации гиперпараметров существуют готовые решения, которые используют различные методы black-box оптимизации. Разберем одну из наиболее популярных библиотек — Optuna 🛠️[doc].
Есть интеграции с scikit-learn, XGBoost и LightGBM, но мы рассмотрим общий случай, который подойдет для любой модели, даже нейронной сети.
!pip install --quiet optuna
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 380.1/380.1 kB 5.6 MB/s eta 0:00:00 ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 233.4/233.4 kB 8.0 MB/s eta 0:00:00 ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 78.8/78.8 kB 7.4 MB/s eta 0:00:00
import optuna
from optuna.samplers import RandomSampler
# Define function which will optimized
def objective(trial):
# boundaries for the optimizer's
depth = trial.suggest_int("depth", 5, 9, step=1)
min_data_in_leaf = trial.suggest_int("min_data_in_leaf", 6, 14, step=2)
l2_leaf_reg = trial.suggest_categorical("l2_leaf_reg", [2, 5, 7, 10])
random_strength = trial.suggest_float("random_strength", 1, 4)
# create new model(and all parameters) every iteration
model = catboost.CatBoostRegressor(
iterations=2000,
learning_rate=0.1,
depth=depth,
min_data_in_leaf=min_data_in_leaf,
l2_leaf_reg=l2_leaf_reg,
random_strength=random_strength,
random_state=42,
verbose=0,
)
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
boot_score = bootstrap_metric(
y_test,
y_pred,
metric_fn=lambda x, y: mean_squared_error(y_true=x, y_pred=y),
)
return boot_score.mean()
# Create "exploration"
study = optuna.create_study(
direction="minimize", study_name="Optimizer", sampler=RandomSampler(42)
)
study.optimize(
objective, n_trials=20
) # The more iterations, the higher the chances of catching the most optimal hyperparameters
[I 2024-04-15 15:47:33,156] A new study created in memory with name: Optimizer
[I 2024-04-15 15:47:43,719] Trial 0 finished with value: 0.18778714823469753 and parameters: {'depth': 6, 'min_data_in_leaf': 14, 'l2_leaf_reg': 2, 'random_strength': 1.1742508365045983}. Best is trial 0 with value: 0.18778714823469753.
[I 2024-04-15 15:48:19,316] Trial 1 finished with value: 0.18693669468985516 and parameters: {'depth': 9, 'min_data_in_leaf': 12, 'l2_leaf_reg': 7, 'random_strength': 1.6370173320348285}. Best is trial 1 with value: 0.18693669468985516.
[I 2024-04-15 15:48:26,256] Trial 2 finished with value: 0.18927982629776083 and parameters: {'depth': 5, 'min_data_in_leaf': 6, 'l2_leaf_reg': 5, 'random_strength': 2.8355586841671383}. Best is trial 1 with value: 0.18693669468985516.
[I 2024-04-15 15:48:34,677] Trial 3 finished with value: 0.1896157694362379 and parameters: {'depth': 5, 'min_data_in_leaf': 8, 'l2_leaf_reg': 7, 'random_strength': 2.5427033152408347}. Best is trial 1 with value: 0.18693669468985516.
[I 2024-04-15 15:48:48,457] Trial 4 finished with value: 0.18664345988849113 and parameters: {'depth': 7, 'min_data_in_leaf': 6, 'l2_leaf_reg': 10, 'random_strength': 3.896896099223678}. Best is trial 4 with value: 0.18664345988849113.
[I 2024-04-15 15:49:24,346] Trial 5 finished with value: 0.19066900464033307 and parameters: {'depth': 9, 'min_data_in_leaf': 8, 'l2_leaf_reg': 5, 'random_strength': 2.4855307303338106}. Best is trial 4 with value: 0.18664345988849113.
[I 2024-04-15 15:49:32,769] Trial 6 finished with value: 0.18974043932643975 and parameters: {'depth': 5, 'min_data_in_leaf': 14, 'l2_leaf_reg': 5, 'random_strength': 2.640130838029839}. Best is trial 4 with value: 0.18664345988849113.
[I 2024-04-15 15:49:39,793] Trial 7 finished with value: 0.18890967215472124 and parameters: {'depth': 5, 'min_data_in_leaf': 14, 'l2_leaf_reg': 5, 'random_strength': 3.7656227050693505}. Best is trial 4 with value: 0.18664345988849113.
[I 2024-04-15 15:49:48,484] Trial 8 finished with value: 0.19106082064237848 and parameters: {'depth': 5, 'min_data_in_leaf': 6, 'l2_leaf_reg': 7, 'random_strength': 3.486212527455788}. Best is trial 4 with value: 0.18664345988849113.
[I 2024-04-15 15:49:59,003] Trial 9 finished with value: 0.18513876511980235 and parameters: {'depth': 6, 'min_data_in_leaf': 8, 'l2_leaf_reg': 7, 'random_strength': 3.960660809801552}. Best is trial 9 with value: 0.18513876511980235.
[I 2024-04-15 15:50:19,575] Trial 10 finished with value: 0.18764075662934182 and parameters: {'depth': 8, 'min_data_in_leaf': 6, 'l2_leaf_reg': 5, 'random_strength': 3.3138110400578373}. Best is trial 9 with value: 0.18513876511980235.
[I 2024-04-15 15:50:27,876] Trial 11 finished with value: 0.18874053344052916 and parameters: {'depth': 5, 'min_data_in_leaf': 8, 'l2_leaf_reg': 5, 'random_strength': 1.1906750508580708}. Best is trial 9 with value: 0.18513876511980235.
[I 2024-04-15 15:50:38,322] Trial 12 finished with value: 0.18758412555469828 and parameters: {'depth': 6, 'min_data_in_leaf': 8, 'l2_leaf_reg': 7, 'random_strength': 1.358782737814905}. Best is trial 9 with value: 0.18513876511980235.
[I 2024-04-15 15:51:00,259] Trial 13 finished with value: 0.18640431338567243 and parameters: {'depth': 8, 'min_data_in_leaf': 12, 'l2_leaf_reg': 5, 'random_strength': 2.282623055075649}. Best is trial 9 with value: 0.18513876511980235.
[I 2024-04-15 15:51:07,211] Trial 14 finished with value: 0.1892175840186519 and parameters: {'depth': 5, 'min_data_in_leaf': 6, 'l2_leaf_reg': 5, 'random_strength': 3.722699421778279}. Best is trial 9 with value: 0.18513876511980235.
[I 2024-04-15 15:51:17,687] Trial 15 finished with value: 0.18792097589296453 and parameters: {'depth': 6, 'min_data_in_leaf': 10, 'l2_leaf_reg': 2, 'random_strength': 1.4836638617620133}. Best is trial 9 with value: 0.18513876511980235.
[I 2024-04-15 15:51:53,557] Trial 16 finished with value: 0.18996740340882923 and parameters: {'depth': 9, 'min_data_in_leaf': 14, 'l2_leaf_reg': 5, 'random_strength': 3.677676995469933}. Best is trial 9 with value: 0.18513876511980235.
[I 2024-04-15 15:52:07,475] Trial 17 finished with value: 0.18536926971882747 and parameters: {'depth': 7, 'min_data_in_leaf': 14, 'l2_leaf_reg': 2, 'random_strength': 2.281323365878769}. Best is trial 9 with value: 0.18513876511980235.
[I 2024-04-15 15:52:42,816] Trial 18 finished with value: 0.18923370980280027 and parameters: {'depth': 9, 'min_data_in_leaf': 14, 'l2_leaf_reg': 5, 'random_strength': 1.3595961020010483}. Best is trial 9 with value: 0.18513876511980235.
[I 2024-04-15 15:52:53,161] Trial 19 finished with value: 0.18768378941420918 and parameters: {'depth': 6, 'min_data_in_leaf': 14, 'l2_leaf_reg': 7, 'random_strength': 3.915346248162882}. Best is trial 9 with value: 0.18513876511980235.
Давайте посмотрим на историю оптимизации нашей метрики:
optuna.visualization.plot_optimization_history(study)
Можем посмотреть, с какими параметрами какие результаты получились, и сделать выводы, в каких диапазонах лучше подбирать параметры:
params = ["depth", "min_data_in_leaf", "l2_leaf_reg", "random_strength"]
optuna.visualization.plot_slice(study, params=params, target_name="mean_squared_error")
Выведем лучшие параметры:
# show best params
study.best_params
{'depth': 6,
'min_data_in_leaf': 8,
'l2_leaf_reg': 7,
'random_strength': 3.960660809801552}
Optuna оценивает важность параметров для лучшего результата:
optuna.visualization.plot_param_importances(study)
Обучим CatBoost на значениях, подобранных Optuna:
models_add5 = {}
models_add5["catboost_tuned"] = catboost.CatBoostRegressor(
iterations=2000,
learning_rate=0.1,
depth=study.best_params["depth"],
min_data_in_leaf=study.best_params["min_data_in_leaf"],
l2_leaf_reg=study.best_params["l2_leaf_reg"],
random_strength=study.best_params["random_strength"],
random_state=42,
verbose=0,
)
# task_type="GPU") # can use gpu, but no parallel-cpu option
cat_tuned_add = train_and_test_regressor(models_add5, x_train, y_train, x_test, y_test)
Fitting catboost_tuned Calculating bootstrap score for catboost_tuned
plt.figure(figsize=(16, 6))
ax = sns.boxplot(
data=pd.concat([tuned_boost, xgb_add, xgb_add2, lgb_add, cat_add, cat_tuned_add]),
y="mse",
x="model",
hue="model",
)
plt.setp(ax.get_xticklabels(), rotation=45)
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("Boosting and others", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
Качество незначительно улучшилось
Каждый из модифицированных бустингов имеет свои особые параметры и рекомендации от создателей и участников Kaggle, как и в каком порядке выбирать параметры для конкретного бустинга. Если вы решили использовать тот или иной вид бустинга в своей задаче, ОЗНАКОМЬТЕСЬ c этими советами.
Все три бустинга, к примеру, позволяют задавать не только число признаков, использующихся в каждом узле, но и число признаков, использующихся в каждом дереве в целом.
Кроме того, все три бустинга имеют настройки, ускоряющие их работу (у LightGBM эти настройки выставлены по умолчанию), и все три бустинга умеют работать на GPU.
Здесь мы бегло пробежались по самым верхам, копируя подобранные на предыдущих этапах параметры.
В XGBoost и LightGBM есть свои, более быстрые и иногда более эффективные реализации случайного леса. Но их надо дополнительно настраивать.
models_rf = {}
models_rf["xgb_rf"] = xgboost.XGBRFRegressor(
n_estimators=250,
colsample_bytree=0.8,
subsample=0.8,
reg_lambda=0.001, # to get deeper, less regularized trees
max_depth=20, # trees must be deep
n_jobs=-1,
objective="reg:squarederror",
)
models_rf["lgb_rf"] = lightgbm.LGBMRegressor(
n_estimators=250,
subsample_freq=1, # for lgb random forest must be set to 1
num_leaves=2**14, # don't forget to change the number of leaves to smth big
boosting_type="rf", # set boosteer type
colsample_bytree=0.8, # for lgb random forest must be less then 1
subsample=0.8, # for lgb random forest must be less then 1
min_child_samples=1, # to get deeper trees
n_jobs=-1,
force_col_wise=True,
verbose=-1,
)
rf_add = train_and_test_regressor(models_rf, x_train, y_train, x_test, y_test)
Fitting xgb_rf Fitting lgb_rf Calculating bootstrap score for xgb_rf Calculating bootstrap score for lgb_rf
plt.figure(figsize=(16, 6))
sns.boxplot(
data=pd.concat([tuned_boost.query('model == "RF"'), rf_add]),
y="mse",
x="model",
hue="model",
)
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("Boosting and others", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
Заметьте, что в данном случае они показывают себя иначе, нежели sklearn.RandomForest. Это частое явление, так как деревья в пакетах XGBoost и LightGBM строятся отличным от sklearn образом. Это может как улучшать качество, так и ухудшать.
Смесь экспертов

До этого мы использовали два подхода. Первый подход — берем много предсказаний большого количества моделей и усредняем (считаем, что модели равноправны).
$$\large h(x) = \dfrac 1 k \sum_{i=i}^k a_i (x) $$Потом задумываемся о том, что каждая модель предсказывает в целом по-разному. Одна модель ошибается в $10\%$ случаев, другая — в $15\%$ и так далее. Было бы неплохо к предсказаниям этих моделей подобрать веса. Так рождается идея того же бустинга.
$$\large h(x) = \sum_{i=i}^k b_i a_i (x) $$Следующий логичный шаг — подумать о том, что каждая модель может ошибаться на каких-то своих объектах. Например, при предсказании, насколько велика вероятность, что человек серьезно заболеет, одна модель будет плохо работать для европейцев, а другая — для жителей Новой Гвинеи.
$$\large h(x) = \sum_{i=i}^k b_i(x) a_i (x) $$Получается ситуация, в которой то, насколько хорошо будет предсказывать модель, зависит от самого объекта. Фактически это означает то, что мы бы хотели для каждого объекта получать какой-то вектор весов, а дальше суммировать предсказания моделей $a_i$, используя эти веса.
Как получать эти веса для каждого объекта? Обучим еще одну модель, которая явно или неявно предсказывает веса алгоритмов и агрегирует их предсказания. Называться она будет мета-алгоритмом.
Обычно в качестве мета-алгоритма используются сравнительно простые модели, например, линейные.
Как получить такую модель? Есть два распространенных подхода — stacking и blending
На соревновании Netflix Prize была поставлена задача — предсказать, как люди оценят тот или иной фильм. Победил подход, основанный на таком объединении моделей, при котором у вас каждая модель получает вес в зависимости от объекта. Подход называется блендинг.
Отличительной особенностью такого способа ансамблирования является использование моделей разной природы.
Разберем пошагово, как реализуется блендинг:



Недостатком блендинга является то, что мы дополнительно разбиваем обучающую выборку, так как нельзя учить и базовые алгоритмы, и мета-алгоритм на одних и тех же данных.
Для улучшения качества можно сделать несколько блендингов (по-разному разбивая обучающую выборку на подвыборки), а дальше усреднять предсказания разных блендингов.
Попробуем сделать простой блендинг. Единственное, немного схитрим. Для обучения мета-алгоритма будем использовать датасет, который использовали при подборе гиперпараметров алгоритмов
class BlendingRegressor:
def __init__(self, first_layer_models, second_layer_model):
self.first_layer_models = {
name: sklearn.clone(model) for name, model in first_layer_models.items()
}
self.second_layer_model = sklearn.clone(second_layer_model)
def fit_1st_layer(self, x, y):
for name, model in self.first_layer_models.items():
print(f"Fitting {name}")
model.fit(x, y)
def predict_1st_layer(self, x):
features = np.zeros((x.shape[0], len(self.first_layer_models)))
for ind, model in enumerate(self.first_layer_models.values()):
features[:, ind] = model.predict(x)
return features
def fit_2nd_layer(self, x, y):
features = self.predict_1st_layer(x)
self.second_layer_model.fit(features, y)
def predict(self, x):
features = self.predict_1st_layer(x)
y_pred = self.second_layer_model.predict(features)
return y_pred
first_layer_models = {}
first_layer_models["linreg"] = make_pipeline(
StandardScaler(with_mean=False), LinearRegression()
)
first_layer_models["rf"] = RandomForestRegressor(
n_estimators=250, max_depth=None, min_samples_leaf=1, n_jobs=-1, random_state=42
)
first_layer_models["xgb"] = xgboost.XGBRegressor(
n_estimators=500,
learning_rate=0.1,
max_depth=5,
random_state=42,
min_child_weight=10,
n_jobs=-1,
objective="reg:squarederror",
)
first_layer_models["lgb_tuned"] = lightgbm.LGBMRegressor(
n_estimators=2000,
learning_rate=0.1,
max_depth=-1,
num_leaves=12,
random_state=42,
min_child_weight=7,
n_jobs=-1,
force_col_wise=True,
verbose=-1,
)
first_layer_models["catboost"] = catboost.CatBoostRegressor(
iterations=2000,
verbose=0,
learning_rate=0.1,
depth=5,
random_state=42,
min_data_in_leaf=5,
)
x_learn, x_valid, y_learn, y_valid = train_test_split(x_train, y_train, random_state=42)
blend_reg = BlendingRegressor(first_layer_models, LinearRegression())
blend_reg.fit_1st_layer(x_learn, y_learn)
blend_reg.fit_2nd_layer(x_valid, y_valid)
y_pred = blend_reg.predict(x_test)
blend_boot = bootstrap_metric(
y_test, y_pred, metric_fn=lambda x, y: mean_squared_error(y_true=x, y_pred=y)
)
Fitting linreg Fitting rf Fitting xgb Fitting lgb_tuned Fitting catboost
blend_data = pd.DataFrame({"mse": blend_boot})
blend_data["model"] = "SingleBlending"
plt.figure(figsize=(16, 6))
ax = sns.boxplot(
data=pd.concat([tuned_boost, xgb_add, xgb_add2, lgb_add, cat_add, blend_data]),
y="mse",
x="model",
hue="model",
)
plt.setp(ax.get_xticklabels(), rotation=45)
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("Boosting and others", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
Одиночный блендинг работает даже хуже, чем один CatBoost
Попробуем обучить 10 блендингов с разными разбиениями x_train на x_learn и x_valid:
from IPython.display import clear_output
blending_ensemble = []
# takes some time to run
for i in range(1, 11):
print(f"Training blending {i}")
x_learn, x_valid, y_learn, y_valid = train_test_split(
x_train, y_train, random_state=i * 7 % 13
)
blend_reg = BlendingRegressor(first_layer_models, LinearRegression())
blend_reg.fit_1st_layer(x_learn, y_learn)
blend_reg.fit_2nd_layer(x_valid, y_valid)
blending_ensemble.append(blend_reg)
clear_output()
y_pred = 0
for blend_reg in blending_ensemble:
y_pred += blend_reg.predict(x_test)
y_pred /= len(blending_ensemble)
eblend_boot = bootstrap_metric(
y_test, y_pred, metric_fn=lambda x, y: mean_squared_error(y_true=x, y_pred=y)
)
eblend_data = pd.DataFrame({"mse": eblend_boot})
eblend_data["model"] = "EnsembleBlending"
np.quantile(eblend_boot, q=[0.025, 0.975])
array([0.17030973, 0.20092833])
np.quantile(cat_add["mse"], q=[0.025, 0.975])
array([0.1724967 , 0.20468458])
plt.figure(figsize=(16, 6))
ax = sns.boxplot(
data=pd.concat(
[tuned_boost, xgb_add, xgb_add2, lgb_add, cat_add, blend_data, eblend_data]
),
y="mse",
x="model",
hue="model",
)
plt.setp(ax.get_xticklabels(), rotation=45)
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("Boosting and others", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
Качество по сравнению с лучшей моделью (CatBoost) существенно не отличается.
Также можно использовать другой способ, который позволяет использовать всю обучающую выборку.
Вместо того, чтобы делить обучающую выборку на подвыборки, давайте использовать кросс-валидацию.
Для этого:

Обучаем базовую модель из ансамбля на каждом кросс-валидационном разбиении.
На блоке, который не вошел в обучение, делаем предсказание. Получаем предсказания для всех объектов обучающей выборки. Повторяем процедуру для каждой модели в ансамбле.



Стэкинг, в отличие от блендинга, использует всю тренировочную выборку.
Но этим мы вносим несколько проблем, одной из которых является то, что ансамбль, на предсказаниях которого мы учили мета-алгоритм, и ансамбль, предсказания которого мы в итоге используем, немного отличаются.
Такой подход более склонен к переобучению. Для борьбы с ним можно, к примеру, подмешивать к предсказаниям базовых моделей шум.
Также, по причине того, что нам надо делать предсказание на кросс-валидации, работать этот метод будет дольше, чем Blending.
В sklearn уже реализован свой StackingRegressor, поэтому в этой лекции мы его реализовывать не будем.
Можете посмотреть пример реализации, например, здесь 🐾[git]. Если вам действительно понадобится стэкинг, полезно иметь свою собственную реализацию, чтобы легко менять в ней некоторые детали (вариантов стекинга великое множество).
Возьмем в нашу новую модель только быстро обучащиеся модели
base_models = []
base_models.append(
["linreg", make_pipeline(StandardScaler(with_mean=False), LinearRegression())]
)
base_models.append(
[
"xgb",
xgboost.XGBRegressor(
n_estimators=500,
learning_rate=0.1,
max_depth=5,
random_state=42,
min_child_weight=10,
n_jobs=-1,
objective="reg:squarederror",
),
]
)
base_models.append(
[
"lgb",
lightgbm.LGBMRegressor(
n_estimators=2000,
learning_rate=0.1,
max_depth=-1,
num_leaves=12,
random_state=42,
min_child_weight=7,
n_jobs=-1,
verbose=-1,
),
]
)
base_models.append(
[
"cgb",
catboost.CatBoostRegressor(
iterations=2000,
verbose=0,
learning_rate=0.1,
depth=5,
random_state=42,
min_data_in_leaf=5,
),
]
)
from sklearn.ensemble import StackingRegressor
stacking_reg = StackingRegressor(base_models, LinearRegression(), cv=3)
stacking_reg.fit(x_train, y_train)
StackingRegressor(cv=3,
estimators=[['linreg',
Pipeline(steps=[('standardscaler',
StandardScaler(with_mean=False)),
('linearregression',
LinearRegression())])],
['xgb',
XGBRegressor(base_score=None, booster=None,
callbacks=None,
colsample_bylevel=None,
colsample_bynode=None,
colsample_bytree=None, device=None,
early_stopping_rounds=None,
enable_categorical=False,...
min_child_weight=10, missing=nan,
monotone_constraints=None,
multi_strategy=None,
n_estimators=500, n_jobs=-1,
num_parallel_tree=None,
random_state=42, ...)],
['lgb',
LGBMRegressor(min_child_weight=7,
n_estimators=2000, n_jobs=-1,
num_leaves=12, random_state=42,
verbose=-1)],
['cgb',
<catboost.core.CatBoostRegressor object at 0x7be77de98730>]],
final_estimator=LinearRegression())In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. StackingRegressor(cv=3,
estimators=[['linreg',
Pipeline(steps=[('standardscaler',
StandardScaler(with_mean=False)),
('linearregression',
LinearRegression())])],
['xgb',
XGBRegressor(base_score=None, booster=None,
callbacks=None,
colsample_bylevel=None,
colsample_bynode=None,
colsample_bytree=None, device=None,
early_stopping_rounds=None,
enable_categorical=False,...
min_child_weight=10, missing=nan,
monotone_constraints=None,
multi_strategy=None,
n_estimators=500, n_jobs=-1,
num_parallel_tree=None,
random_state=42, ...)],
['lgb',
LGBMRegressor(min_child_weight=7,
n_estimators=2000, n_jobs=-1,
num_leaves=12, random_state=42,
verbose=-1)],
['cgb',
<catboost.core.CatBoostRegressor object at 0x7be77de98730>]],
final_estimator=LinearRegression())StandardScaler(with_mean=False)
LinearRegression()
XGBRegressor(base_score=None, booster=None, callbacks=None,
colsample_bylevel=None, colsample_bynode=None,
colsample_bytree=None, device=None, early_stopping_rounds=None,
enable_categorical=False, eval_metric=None, feature_types=None,
gamma=None, grow_policy=None, importance_type=None,
interaction_constraints=None, learning_rate=0.1, max_bin=None,
max_cat_threshold=None, max_cat_to_onehot=None,
max_delta_step=None, max_depth=5, max_leaves=None,
min_child_weight=10, missing=nan, monotone_constraints=None,
multi_strategy=None, n_estimators=500, n_jobs=-1,
num_parallel_tree=None, random_state=42, ...)LGBMRegressor(min_child_weight=7, n_estimators=2000, n_jobs=-1, num_leaves=12,
random_state=42, verbose=-1)<catboost.core.CatBoostRegressor object at 0x7be77de98730>
LinearRegression()
y_pred = stacking_reg.predict(x_test)
print(mean_squared_error(y_true=y_test, y_pred=y_pred))
0.18667403449277847
stack_boot = bootstrap_metric(
y_test, y_pred, metric_fn=lambda x, y: mean_squared_error(y_true=x, y_pred=y)
)
stack_data = pd.DataFrame({"mse": stack_boot})
stack_data["model"] = "Stacking"
plt.figure(figsize=(18, 6))
ax = sns.boxplot(
data=pd.concat(
[
tuned_boost,
xgb_add,
xgb_add2,
lgb_add,
cat_add,
blend_data,
eblend_data,
stack_data,
]
),
y="mse",
x="model",
hue="model",
palette="tab10",
)
plt.setp(ax.get_xticklabels(), rotation=45)
plt.xlabel("", size=20)
plt.ylabel("MSE", size=20)
plt.title("Boosting and others", size=20)
plt.tick_params(axis="both", which="major", labelsize=14)
plt.xticks(size=20)
plt.show()
np.quantile(stack_data["mse"], q=[0.025, 0.975])
array([0.17165493, 0.2022846 ])
np.quantile(cat_add["mse"], q=[0.025, 0.975])
array([0.1724967 , 0.20468458])
Видим, что стэкинг в данной задаче не принес существенного улучшения.
На самом деле эти подходы часто объединяют в один или путают местами. Например, улучшая блендинг в сторону использования всей обучающей выборки, можно получить стэкинг.
Оба подхода имеют множество модификаций, к примеру, с добавлением признаков-предсказаний базовых моделей к исходным признакам и т. д. Оба подхода показывают схожие результаты. И оба подхода улучшают свое качество по мере увеличения размера обучающей выборки.
Идея ансамблирования будет довольно часто встречаться в различных подходах в машинном обучении. Мы рассмотрели основные базовые концепции, которые помогут в понимании более сложных. При достижении "потолка" в качестве вашей модели полезно подумать в сторону ансамблирования для улучшения качества.
Из практики соревнований по машинному обучению ✏️[blog] известно, что использование градиентного бустинга для решения задач с табличными данными даёт возможность получить максимально качественное решение. Тем не менее, следует понимать, что это гипотетическое лучшее качество решения достигается путём сложного подбора параметров и финальной настройки модели.
В качестве короткой практической рекомендации можно сформулировать следующий пайплайн для решения задачи на реальных табличных данных:
Как мы уже успели установить выше, справедливо разложение:
ошибка предсказания модели = bias + variance
и имеет место явление bias-variance tradeoff, принципиально не позволяющее одинаково сильно минимизировать оба вклада в ошибку предсказания модели.
Ансамблирование в виде бэггинга, использующееся при построении RF, заточено на уменьшение variance путём "усреднения" ответов элементарных предсказателей. Использование бэггинга существенно не позволяет улучшить bias — этот показатель наследуется от базового эстиматора. Таким образом, при построении случайного леса следует взять относительно глубокие деревья решений (можно говорить о глубине в 6–10 ветвлений), обладающие собственным низким показателем bias.
Ансамблирование в виде бустинга, наоборот, в первую очередь заточено на улучшение показателя bias итоговой модели путём взаимного улучшения большого числа стабильных, но слабых эстиматоров (то есть обладающих высоким показателем bias и низким variance). Таким образом, при построении градиентного бустинга над деревьями решений следует взять в качестве базовой модели неглубокие деревья (вплоть до решающих пней — деревьев решений с единственным ветвлением).
Фактически, все реализации алгоритма случайного леса будут содержать три важных гиперпараметра:
Мы ожидаем, что каждое из деревьев в составе леса обладает достаточной обобщающей способностью, чтобы быть принципиально способным самостоятельно предсказывать данные. То есть во время подбора гиперпараметров случайного леса данный параметр стоит постепенно увеличивать, контролируя качество на тренировочной и валидационной выборках — слишком глубокие деревья могут привести к переобучению модели.
Бэггинг деревьев решений позволяет нам минимизировать variance итоговой модели, но понятно, что ресурс для такого улучшения не безграничен. Количество деревьев в лесу можно постепенно увеличивать до тех пор, пока это не перестанет приводить к существенному улучшению качества предсказания модели.
Подавая на вход одиночным деревьям решений большее число признаков, мы делаем их более "сильными предсказателями", но взамен увеличиваем их скоррелированность (тем самым нарушаем процедуру бэггинга). Для конкретных данных положение оптимума можно наверняка установить только полным перебором параметра, но общей практикой является использование трети от общего числа свойств для задачи регрессии и округленного вниз квадратного корня из числа свойств для задач классификации.
Современные реализации GBPD содержат крайне широкий список доступных для настройки параметров. Первичное знакомство с длинными списками параметров может оказаться дезориентирующим, поэтому мы приведём короткий список наиболее существенных гиперпараметров, которые повлияют на успех обучения модели.
Среди таких наиболее важных параметров выделим два класса:
Названия параметров в приведённой ниже таблице являются ссылками на актуальную версию документации:
| param type | CatBoost | XGBoost | LightGBM |
|---|---|---|---|
| overfitting control | learning_ratedepthl2_leaf_reg |
etamax_depthmin_child_weight |
learning_ratemax_depthnum_leavesmin_data_in_leaf |
| speed of the training | rsmiterations |
colsample_bytreesubsamplen_estimators,-%E2%80%93%20Number%20of%20gradient) |
feature_fractionbagging_fraction |
Есть попытки построить архитектуры нейронных сетей таким образом, чтобы они могли работать с табличными данными. Можно отметить архитектуру от Яндекса NODE 🎓[arxiv] и TabNet 🎓[arxiv], TabNet 🐾[git] от Гугл.
Вторая работа особенно удачна и уже активно используется в соревнованиях на Kaggle. Стоит отметить, что победы над древесными моделями не одержано. Но полученная модель иногда достигает их качества и обладает рядом интересных особенностей:
Установим пакет, реализующий эту нейросеть на PyTorch.
!pip install -q pytorch-tabnet
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 44.5/44.5 kB 1.4 MB/s eta 0:00:00
import sklearn
import sklearn.datasets
from sklearn.model_selection import train_test_split
calif_housing = sklearn.datasets.fetch_california_housing()
x = calif_housing.data
y = calif_housing.target
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
x_learn, x_valid, y_learn, y_valid = train_test_split(x_train, y_train, random_state=42)
Запустим с параметрами по умолчанию, передав датасет для валидации. Нам нужно узнать, когда нейросеть начнет переобучаться.
Заметьте, что у XGBoost и LightGBM тоже есть такая возможность early_stopping, которая позволяет легко подбирать число базовых моделей. Подробнее смотрите в документации.
Нейросеть принимает y в формате (предсказываемая величина, число предсказываемых величин), поэтому нам потребуется reshape.
from pytorch_tabnet.tab_model import TabNetRegressor
from warnings import simplefilter
simplefilter("ignore", category=UserWarning)
tabnet = TabNetRegressor()
tabnet.fit(
x_learn, y_learn.reshape(-1, 1), eval_set=[(x_valid, y_valid.reshape(-1, 1))]
)
epoch 0 | loss: 3.46929 | val_0_mse: 81.10814| 0:00:00s epoch 1 | loss: 0.83794 | val_0_mse: 248.88475| 0:00:01s epoch 2 | loss: 0.62641 | val_0_mse: 766.64854| 0:00:02s epoch 3 | loss: 0.52947 | val_0_mse: 2160.5632| 0:00:02s epoch 4 | loss: 0.48285 | val_0_mse: 847.70986| 0:00:03s epoch 5 | loss: 0.45664 | val_0_mse: 144.55513| 0:00:04s epoch 6 | loss: 0.43183 | val_0_mse: 385.16453| 0:00:04s epoch 7 | loss: 0.42237 | val_0_mse: 502.14704| 0:00:05s epoch 8 | loss: 0.40306 | val_0_mse: 328.22527| 0:00:06s epoch 9 | loss: 0.39239 | val_0_mse: 25.22985| 0:00:07s epoch 10 | loss: 0.39024 | val_0_mse: 9.7813 | 0:00:08s epoch 11 | loss: 0.3793 | val_0_mse: 20.9099 | 0:00:09s epoch 12 | loss: 0.37781 | val_0_mse: 35.45243| 0:00:09s epoch 13 | loss: 0.40507 | val_0_mse: 90.62408| 0:00:10s epoch 14 | loss: 0.38813 | val_0_mse: 161.96715| 0:00:11s epoch 15 | loss: 0.38308 | val_0_mse: 322.3198| 0:00:11s epoch 16 | loss: 0.37115 | val_0_mse: 137.86928| 0:00:12s epoch 17 | loss: 0.36739 | val_0_mse: 60.48093| 0:00:13s epoch 18 | loss: 0.36428 | val_0_mse: 14.46909| 0:00:14s epoch 19 | loss: 0.35771 | val_0_mse: 11.60839| 0:00:14s epoch 20 | loss: 0.36193 | val_0_mse: 5.67108 | 0:00:15s epoch 21 | loss: 0.35666 | val_0_mse: 9.47088 | 0:00:16s epoch 22 | loss: 0.40629 | val_0_mse: 9.78177 | 0:00:16s epoch 23 | loss: 0.37677 | val_0_mse: 7.17048 | 0:00:17s epoch 24 | loss: 0.37078 | val_0_mse: 4.78956 | 0:00:18s epoch 25 | loss: 0.36105 | val_0_mse: 5.98444 | 0:00:19s epoch 26 | loss: 0.36529 | val_0_mse: 4.0579 | 0:00:20s epoch 27 | loss: 0.35972 | val_0_mse: 2.40787 | 0:00:21s epoch 28 | loss: 0.34916 | val_0_mse: 2.32834 | 0:00:21s epoch 29 | loss: 0.34694 | val_0_mse: 2.21937 | 0:00:22s epoch 30 | loss: 0.35804 | val_0_mse: 3.103 | 0:00:23s epoch 31 | loss: 0.35602 | val_0_mse: 2.16907 | 0:00:24s epoch 32 | loss: 0.35559 | val_0_mse: 1.86662 | 0:00:24s epoch 33 | loss: 0.34622 | val_0_mse: 1.65947 | 0:00:25s epoch 34 | loss: 0.34326 | val_0_mse: 2.6706 | 0:00:26s epoch 35 | loss: 0.34969 | val_0_mse: 0.92876 | 0:00:26s epoch 36 | loss: 0.34671 | val_0_mse: 1.12267 | 0:00:27s epoch 37 | loss: 0.35364 | val_0_mse: 0.8622 | 0:00:28s epoch 38 | loss: 0.33636 | val_0_mse: 0.72947 | 0:00:28s epoch 39 | loss: 0.32955 | val_0_mse: 0.72095 | 0:00:29s epoch 40 | loss: 0.33472 | val_0_mse: 0.69347 | 0:00:30s epoch 41 | loss: 0.33648 | val_0_mse: 0.52797 | 0:00:31s epoch 42 | loss: 0.33281 | val_0_mse: 0.56917 | 0:00:32s epoch 43 | loss: 0.33248 | val_0_mse: 0.50441 | 0:00:33s epoch 44 | loss: 0.32769 | val_0_mse: 0.56499 | 0:00:33s epoch 45 | loss: 0.32603 | val_0_mse: 0.52375 | 0:00:34s epoch 46 | loss: 0.33023 | val_0_mse: 0.52137 | 0:00:35s epoch 47 | loss: 0.32969 | val_0_mse: 0.47676 | 0:00:35s epoch 48 | loss: 0.33041 | val_0_mse: 0.41541 | 0:00:36s epoch 49 | loss: 0.33465 | val_0_mse: 0.40487 | 0:00:37s epoch 50 | loss: 0.32391 | val_0_mse: 0.39873 | 0:00:38s epoch 51 | loss: 0.32777 | val_0_mse: 0.4173 | 0:00:38s epoch 52 | loss: 0.32818 | val_0_mse: 0.37255 | 0:00:39s epoch 53 | loss: 0.33311 | val_0_mse: 0.36887 | 0:00:40s epoch 54 | loss: 0.32743 | val_0_mse: 0.37582 | 0:00:40s epoch 55 | loss: 0.31586 | val_0_mse: 0.34148 | 0:00:41s epoch 56 | loss: 0.31347 | val_0_mse: 0.36701 | 0:00:42s epoch 57 | loss: 0.31985 | val_0_mse: 0.36415 | 0:00:42s epoch 58 | loss: 0.31901 | val_0_mse: 0.36089 | 0:00:43s epoch 59 | loss: 0.31834 | val_0_mse: 0.33254 | 0:00:44s epoch 60 | loss: 0.31543 | val_0_mse: 0.35125 | 0:00:45s epoch 61 | loss: 0.31736 | val_0_mse: 0.35675 | 0:00:46s epoch 62 | loss: 0.31656 | val_0_mse: 0.33408 | 0:00:47s epoch 63 | loss: 0.31565 | val_0_mse: 0.4354 | 0:00:47s epoch 64 | loss: 0.32943 | val_0_mse: 0.34845 | 0:00:48s epoch 65 | loss: 0.32679 | val_0_mse: 0.35464 | 0:00:49s epoch 66 | loss: 0.33543 | val_0_mse: 0.33844 | 0:00:49s epoch 67 | loss: 0.33703 | val_0_mse: 0.37412 | 0:00:50s epoch 68 | loss: 0.32659 | val_0_mse: 0.32857 | 0:00:51s epoch 69 | loss: 0.31737 | val_0_mse: 0.3489 | 0:00:51s epoch 70 | loss: 0.31337 | val_0_mse: 0.33022 | 0:00:52s epoch 71 | loss: 0.31643 | val_0_mse: 0.34543 | 0:00:53s epoch 72 | loss: 0.31297 | val_0_mse: 0.33281 | 0:00:54s epoch 73 | loss: 0.30811 | val_0_mse: 0.34491 | 0:00:55s epoch 74 | loss: 0.3127 | val_0_mse: 0.33546 | 0:00:55s epoch 75 | loss: 0.323 | val_0_mse: 0.34531 | 0:00:56s epoch 76 | loss: 0.31232 | val_0_mse: 0.34467 | 0:00:57s epoch 77 | loss: 0.31028 | val_0_mse: 0.34478 | 0:00:58s epoch 78 | loss: 0.3104 | val_0_mse: 0.35441 | 0:00:59s Early stopping occurred at epoch 78 with best_epoch = 68 and best_val_0_mse = 0.32857
Обучим теперь на всем тренировочном датасете, поставив число эпох обучения равным тому, что нам сообщила выдача функции
tabnet = TabNetRegressor()
tabnet.fit(x_train, y_train.reshape(-1, 1), max_epochs=53)
epoch 0 | loss: 2.71148 | 0:00:00s epoch 1 | loss: 0.77376 | 0:00:01s epoch 2 | loss: 0.58305 | 0:00:02s epoch 3 | loss: 0.53097 | 0:00:03s epoch 4 | loss: 0.48748 | 0:00:03s epoch 5 | loss: 0.44413 | 0:00:04s epoch 6 | loss: 0.42577 | 0:00:05s epoch 7 | loss: 0.41496 | 0:00:06s epoch 8 | loss: 0.39249 | 0:00:07s epoch 9 | loss: 0.38966 | 0:00:07s epoch 10 | loss: 0.3695 | 0:00:08s epoch 11 | loss: 0.37253 | 0:00:10s epoch 12 | loss: 0.35842 | 0:00:11s epoch 13 | loss: 0.35796 | 0:00:11s epoch 14 | loss: 0.35548 | 0:00:12s epoch 15 | loss: 0.34412 | 0:00:13s epoch 16 | loss: 0.34318 | 0:00:14s epoch 17 | loss: 0.34228 | 0:00:15s epoch 18 | loss: 0.34685 | 0:00:15s epoch 19 | loss: 0.34108 | 0:00:16s epoch 20 | loss: 0.33594 | 0:00:17s epoch 21 | loss: 0.33093 | 0:00:18s epoch 22 | loss: 0.33607 | 0:00:19s epoch 23 | loss: 0.33153 | 0:00:19s epoch 24 | loss: 0.32851 | 0:00:20s epoch 25 | loss: 0.33601 | 0:00:21s epoch 26 | loss: 0.33807 | 0:00:22s epoch 27 | loss: 0.33167 | 0:00:23s epoch 28 | loss: 0.32643 | 0:00:24s epoch 29 | loss: 0.32835 | 0:00:25s epoch 30 | loss: 0.33032 | 0:00:26s epoch 31 | loss: 0.33805 | 0:00:27s epoch 32 | loss: 0.33425 | 0:00:27s epoch 33 | loss: 0.31768 | 0:00:28s epoch 34 | loss: 0.32245 | 0:00:29s epoch 35 | loss: 0.32957 | 0:00:30s epoch 36 | loss: 0.31422 | 0:00:31s epoch 37 | loss: 0.31001 | 0:00:31s epoch 38 | loss: 0.30901 | 0:00:32s epoch 39 | loss: 0.31055 | 0:00:33s epoch 40 | loss: 0.3116 | 0:00:35s epoch 41 | loss: 0.32131 | 0:00:36s epoch 42 | loss: 0.31694 | 0:00:37s epoch 43 | loss: 0.30944 | 0:00:37s epoch 44 | loss: 0.31633 | 0:00:38s epoch 45 | loss: 0.3115 | 0:00:39s epoch 46 | loss: 0.31564 | 0:00:40s epoch 47 | loss: 0.3251 | 0:00:41s epoch 48 | loss: 0.32166 | 0:00:41s epoch 49 | loss: 0.31436 | 0:00:42s epoch 50 | loss: 0.31331 | 0:00:43s epoch 51 | loss: 0.30762 | 0:00:44s epoch 52 | loss: 0.30995 | 0:00:44s
from sklearn.metrics import mean_squared_error
y_pred = tabnet.predict(x_test)
print(mean_squared_error(y_true=y_test, y_pred=y_pred))
0.44523391787833416
Видим, что качество сильно хуже, чем у топ-моделей бустинга. Возможно, надо попробовать параметры, отличные от параметров по умолчанию, или нейронную сеть другой архитектуры!
По сообщениям участников Kaggle, модель все же чаще всего уступает хорошо затюненным бустингам.
Литература
Общие источники
Про деревья решений
Про ансамбли
XGBoost
CatBoost
LightGBM
Дисбаланс классов
Нейронные сети и бустинг