Введение в машинное обучение
Допустим, у нас есть наручный шагомер, который фиксирует перемещения в пространстве. В него встроен акселерометр, который способен фиксировать перемещения по трем осям. На выходе мы получаем сигнал с трёх датчиков.
Если задача состоит в том, чтобы подсчитать количество шагов, то к её решению можно подойти двумя способами.
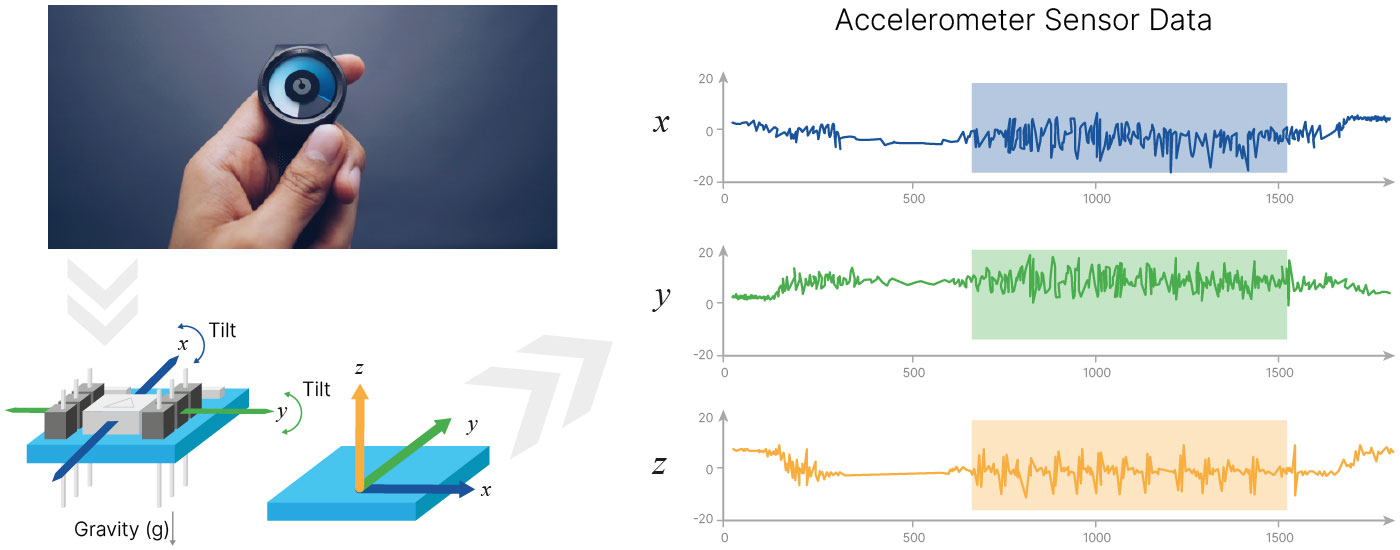
Вариант №1, Классический
Напишем программу. Если появилось ускорение по одной из осей, которое больше определенного порога, то мы создаем то условие, которое срабатывает. Позже мы выясним, что подобные сигнатурные сигналы с датчика могут поступить и при других определенных движениях, не связанных с шагами, например, во время плавания. Добавляется дополнительное условие, которое фильтрует подобные ситуации.
Находятся всё новые и новые исключения из общего правила, программа и ее алгоритмическая сложность будут расти.
Программу будет сложнее поддерживать из-за большого объема кода в ней. Изменение в одной из частей потребует внесение правок в другой код и т.п.
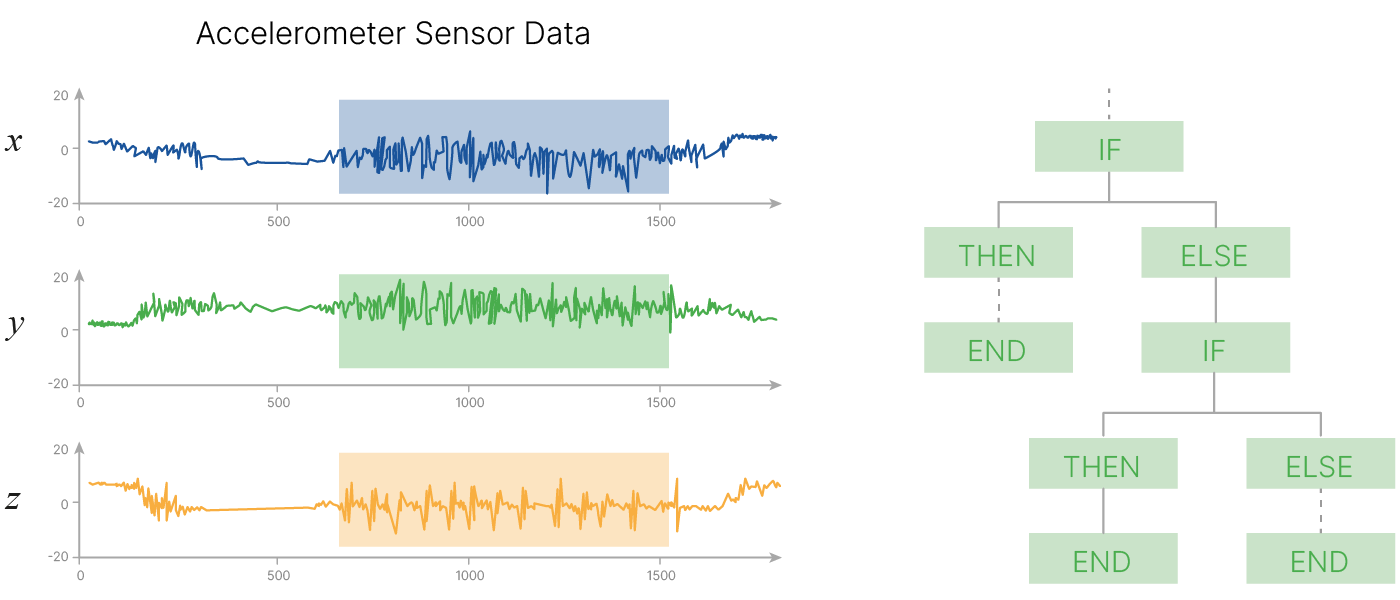
Вариант №2, Машинное обучение
С появлением машинного обучения мы можем применить принципиально другой подход. Не задумываясь о том, что значат показания каждого из акселерометров, мы можем просто собрать некоторый архив данных за определенное время (возможно, разбив на более короткие промежутки времени). Всё, что нам потребуется помимо этих данных — это информация о том, сколько было сделано реальных шагов. После этого данные загружаются в модель, и она на этих данных учится. При достаточном количестве данных и адекватно подобранной модели (чем мы и будем заниматься) мы сможем научить ее решать конкретные задачи (в данном случае — считать шаги).
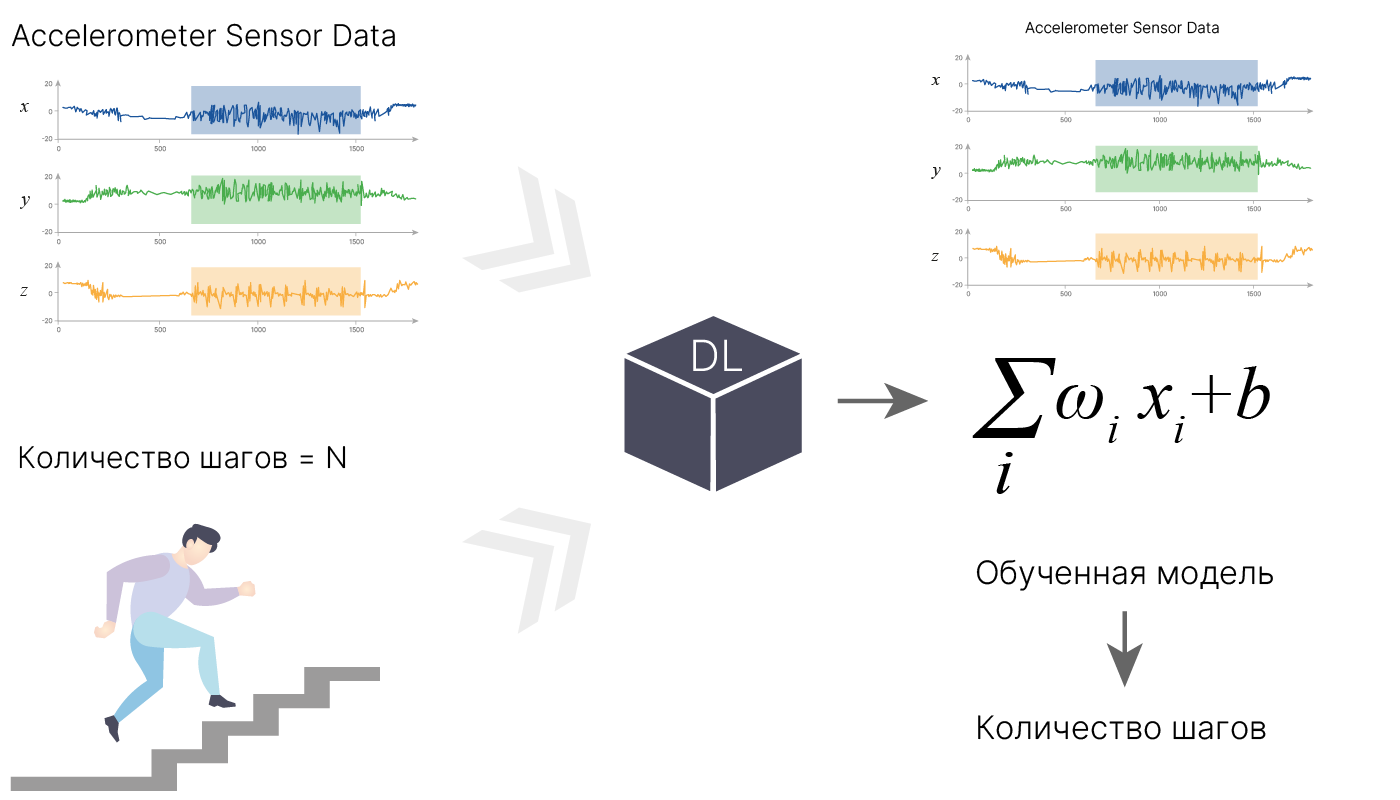
Фактически, мы приближаем реальную функцию $F_{real}$ некоторой функцией $F$: $$\large {F = \sum_i w_{i} x_{i} + b}$$
По сути, модели всё равно, что считать: шаги, сердечный ритм, количество калорий, ударов по клавиатуре и пр. Нет необходимости писать под каждый пример отдельную программу: достаточно собрать данные, и мы сможем решить множество абсолютно разных задач.
Важно лишь понимать, какую модель предпочтительнее выбрать. С этим мы будем разбираться в ходе курса.
Место глубокого обучения и нейронных сетей в ИИ
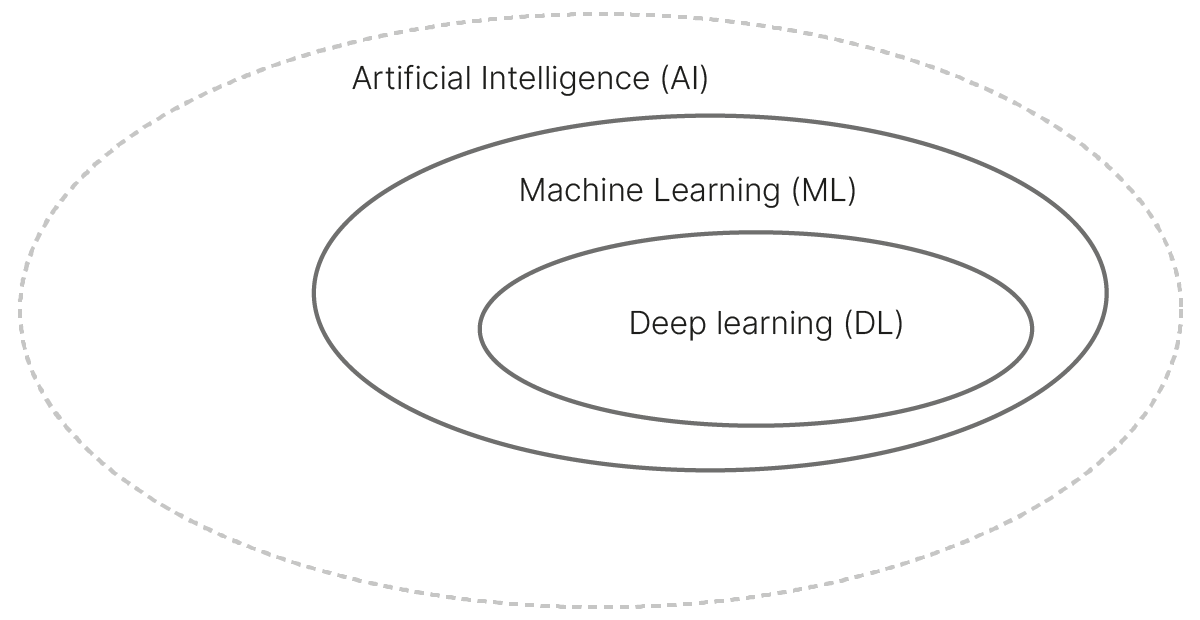
Искусственный интеллект (AI/ИИ) — область IT/Computer science, связанная с моделированием интеллектуальных или творческих видов человеческой деятельности.
Машинное обучение (ML) — подраздел ИИ, связанный с разработкой алгоритмов и статистических моделей, которые компьютерные системы используют для выполнения задач без явных инструкций.
Глубокое обучение (Deep Learning, DL) — совокупность методов машинного обучения, основанных на искуcственных нейронных сетях и обучении представлениям (feature/representation learning). Данный класс методов автоматически выделяет из необработанных данных необходимые признаки (представления), в отличие от методов ML, в которых признаки создают люди вручную (feature engineering).
Существует множество определений сильного и слабого ИИ, рассуждений о появлении искусственного сознания и восстании машин.
Всё намного приземлённее. Есть набор объектов $X$, набор ответов $Y$. Пары "объект-ответ" составляют обучающую выборку.
Мы будем заниматься восстановлением решающей функции $F$, которая переводит признаки $X$, описывающие объекты, в ответы $Y$.
$$ F: X \xrightarrow\ Y $$Позже мы уточним постановку задачи и увидим, что функцию восстанавливаем с погрешностью, в каких-то задачах нет ответов $Y$, а где-то мы создаём новые объекты ${\hat X}$ на основе исходных объектов $X$.
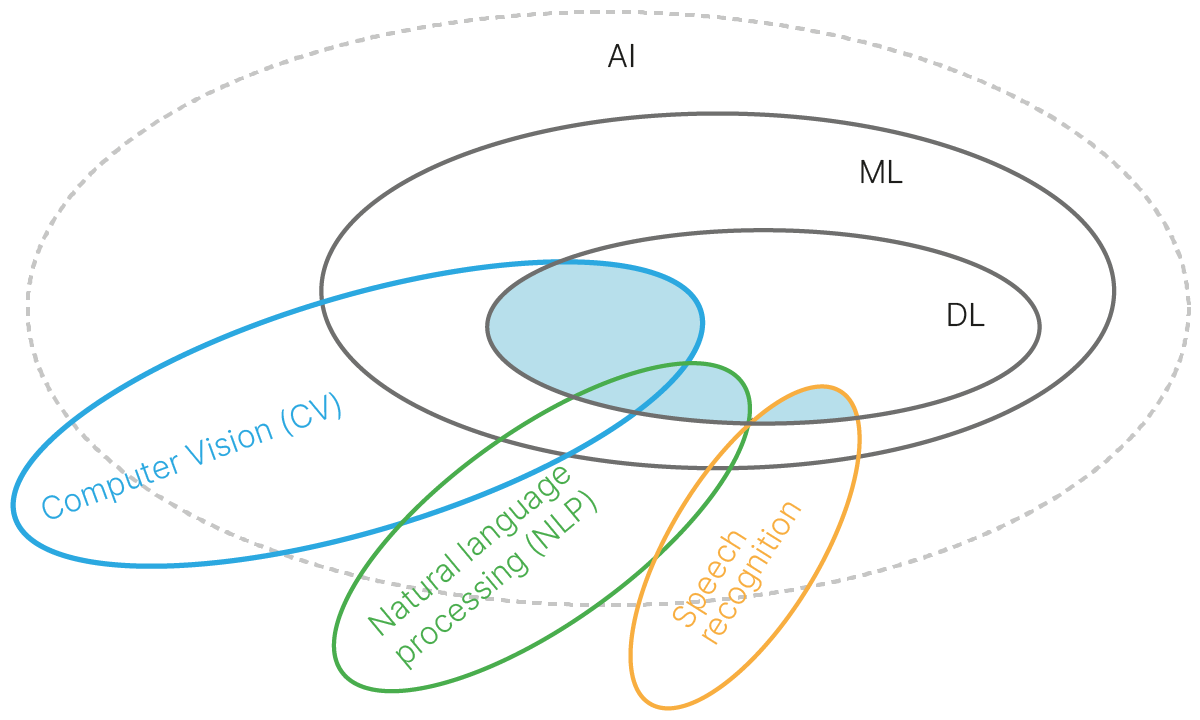
В последнее время именно такого рода модели показывают высокую эффективность в тех областях, с которыми ранее могли справиться только люди. В частности:
Научные исследования таковы, что результаты у них в известной степени непредсказуемы. Одна из задач нашего курса — научиться применять нейросети к решению новых задач, в том числе в областях, где ранее такие технологии активно не использовались.
В первую очередь для нас важны задачи слушателей курса, а успешным прохождением мы считаем решённую научную задачу и написанную по этому поводу статью.
В течение 15-ти лекций мы будем рассказывать теорию и практиковаться, далее плотно займёмся научной работой. Хотя, в целом, её можно начинать уже прямо сейчас.
Преподаватели будут выступать в качестве менторов и помогать вам с выбором подходящих моделей, проверкой гипотез, поиском ошибок. По ходу курса будет несколько воркшопов, где мы всем коллективом будем давать советы по вашим задачам.
Зачем:
Что будет:
Зачем:
Что будет:
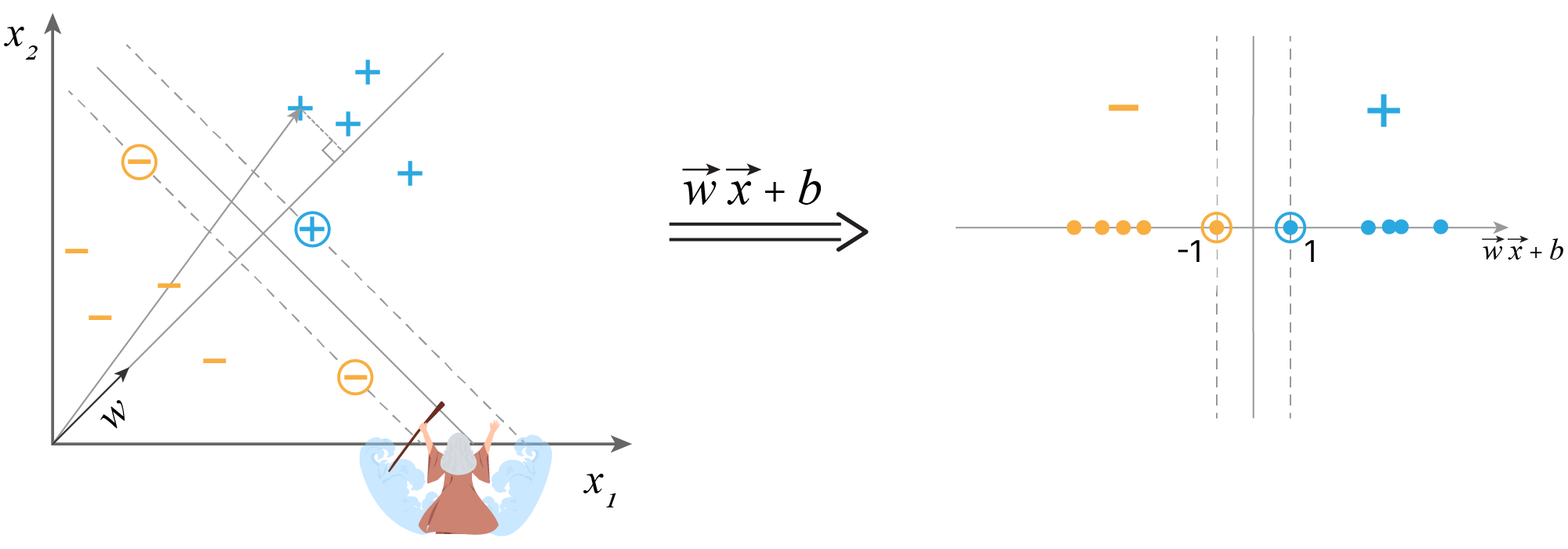
Зачем:
Что будет:
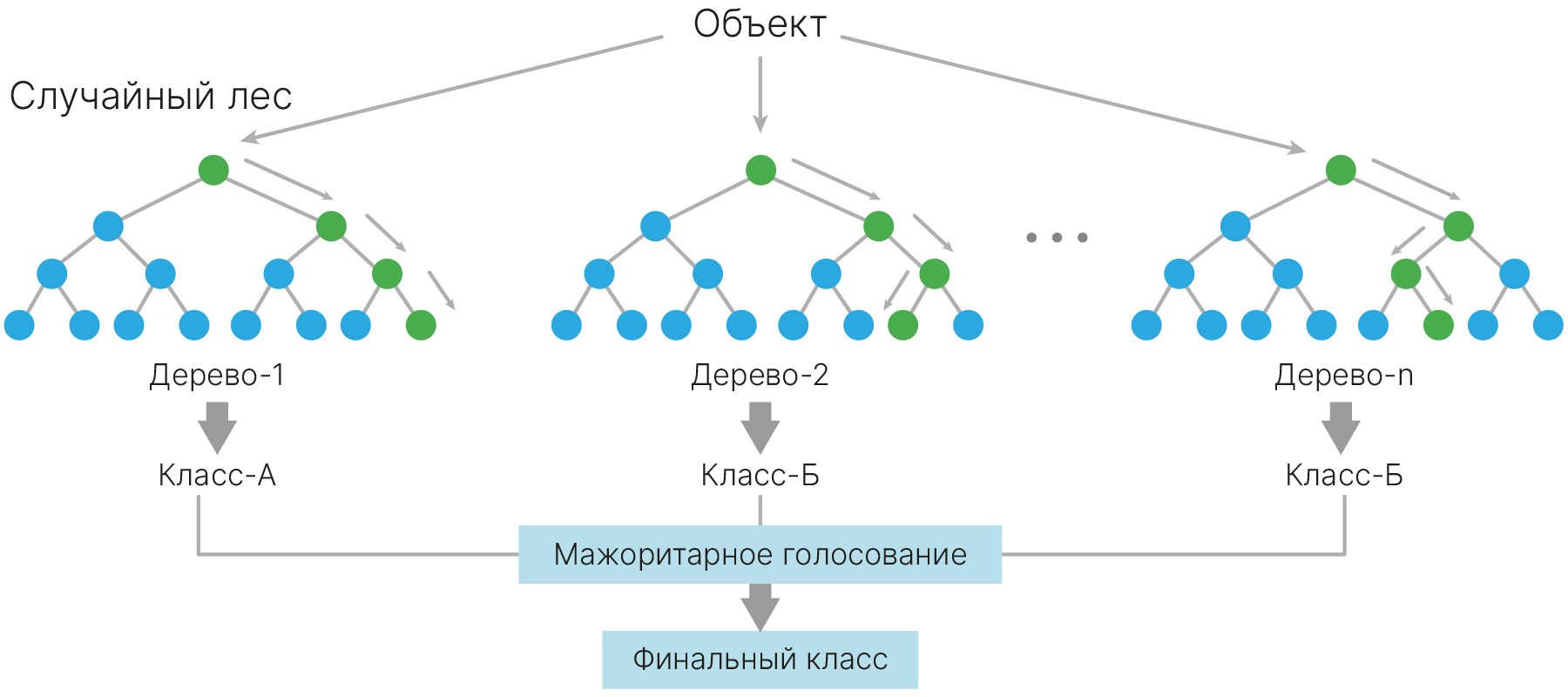
Зачем:
Что будет:
Зачем:
Что будет:
Зачем:
Что будет:

Зачем:
Что будет:
Зачем:
Что будет:

Зачем:
Что будет:
Зачем:
Что будет:
Зачем:
Что будет:
Зачем:
Что будет:
Зачем:
Что будет:

Зачем:
Что будет:
Зачем:
Что будет:
В общем случае задача классификации выглядит следующим образом.
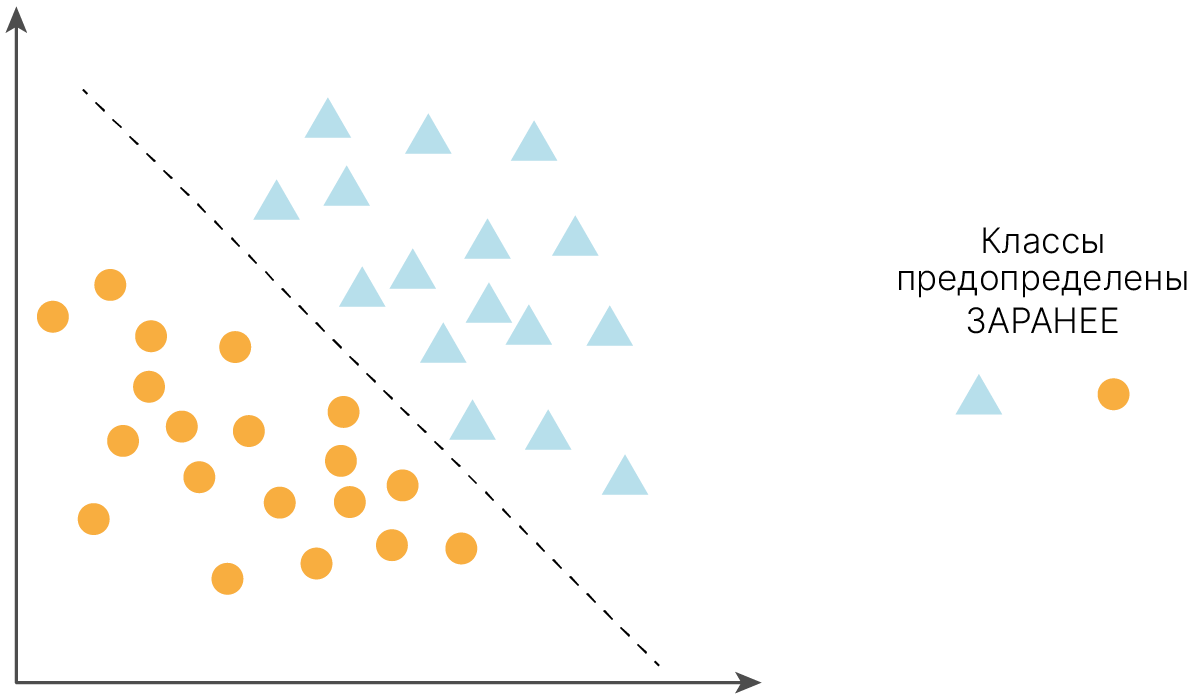
Классификация — отнесение образца к одному из нескольких попарно не пересекающихся множеств.
В качестве образцов могут выступать различные по своей природе объекты, например:
При обучении сети предлагаются пары образец-класс. Образец, как правило, представляется как вектор значений признаков. При этом совокупность всех признаков должна однозначно определять класс, к которому относится образец. В случае, если признаков недостаточно, сеть может соотнести один и тот же образец с несколькими классами, что неверно. По окончании обучения сети ей можно предъявлять неизвестные ранее образцы и получать ответ об их принадлежности к определённому классу.
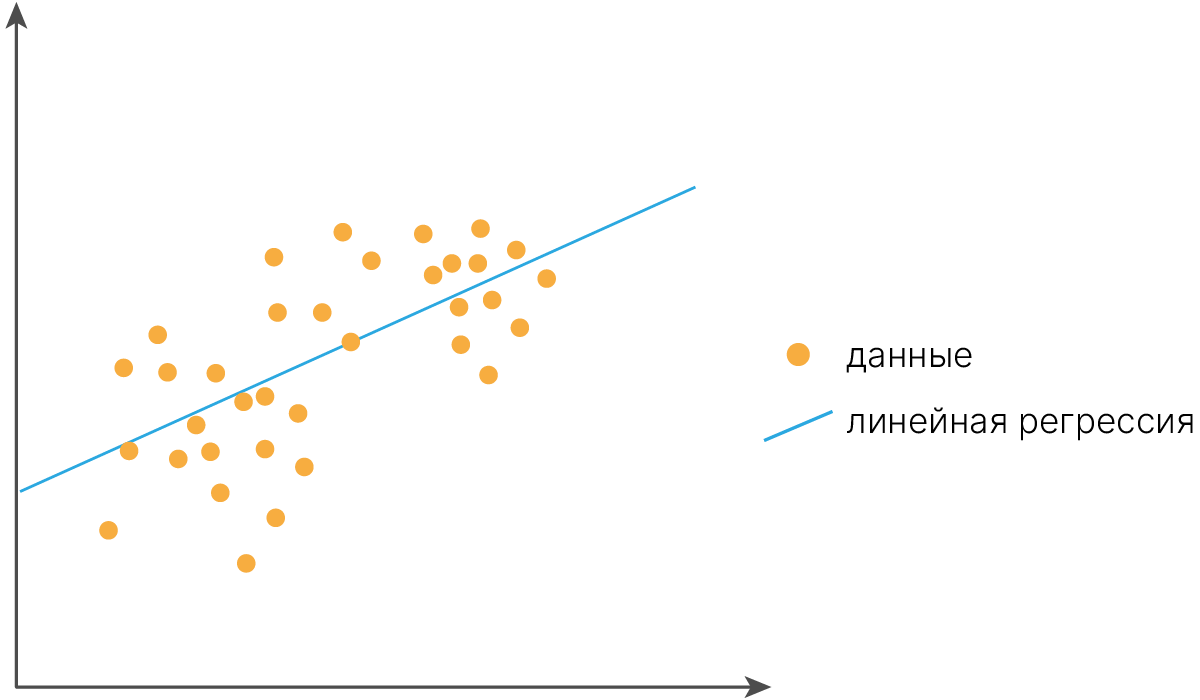
Способности нейронной сети к прогнозированию напрямую следуют из её способности к обобщению и выделению скрытых зависимостей между входными и выходными данными. После обучения сеть способна предсказать будущее значение некой последовательности на основе нескольких предыдущих значений и (или) каких-то существующих в настоящий момент факторов.
Прогнозирование возможно только тогда, когда предыдущие изменения действительно в какой-то степени предопределяют будущие. Например, прогнозирование котировок акций на основе котировок за прошлую неделю может оказаться успешным (а может и не оказаться), тогда как прогнозирование результатов завтрашней лотереи на основе данных за последние 50 лет почти наверняка не даст никаких результатов.
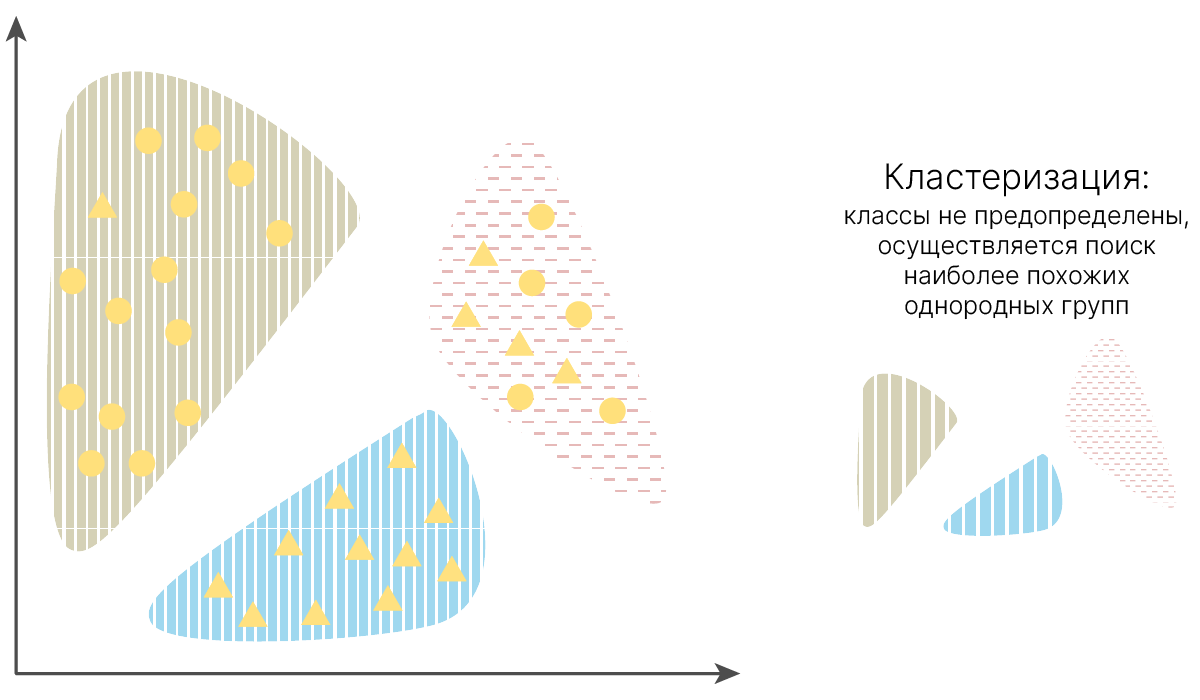
Кластеризация — разбиение множества входных сигналов на классы при том, что ни количество, ни признаки классов заранее не известны. После обучения модель способна определять, к какому классу относится входной сигнал. Модель также может сигнализировать о том, что входной сигнал не относится ни к одному из выделенных классов — это является признаком новых, отсутствующих в обучающей выборке данных. Таким образом, подобная модель может выявлять новые, неизвестные ранее классы сигналов. Соответствие между классами, выделенными сетью, и классами, существующими в предметной области, устанавливается человеком.
Относится к задачам обучения без учителя.
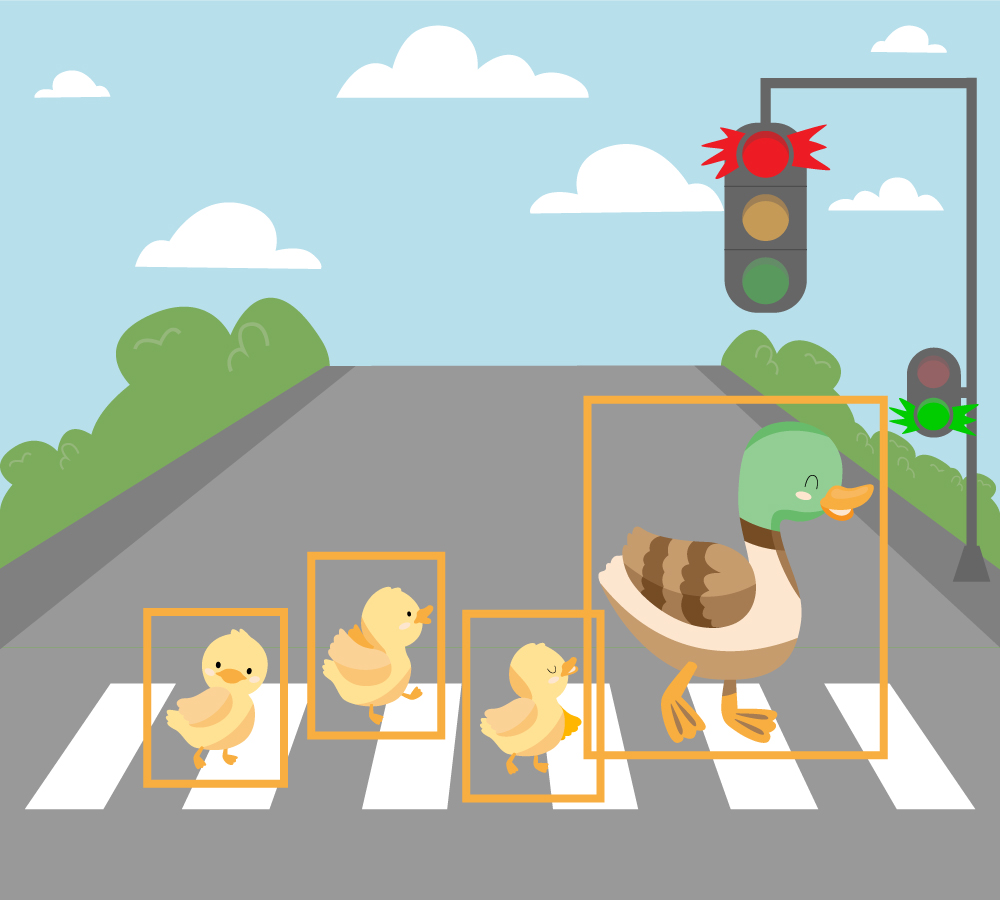
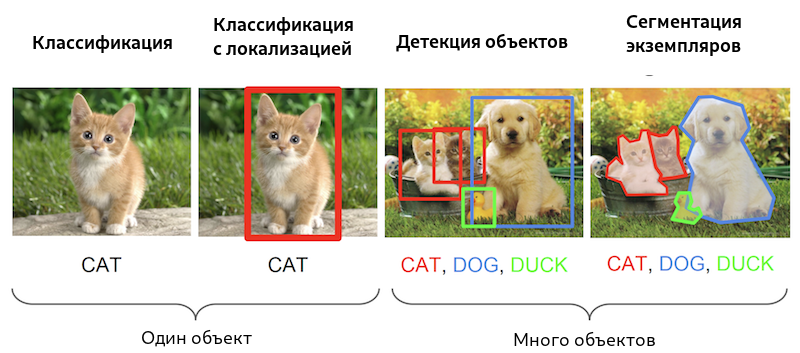
Существуют работы, которые комбинируют в себе несколько задач разом. Типичным примером является задача Object Detection.
Детектирование = Классификация + Регрессия.
Мы отмечаем координаты рамок (регрессия) и классифицируем объект в рамке.
Комбинирование знаний и навыков
Вашим преимуществом станет комбинирование узкоспециализированных знаний в вашей предметной области и машинного обучения.
Одним из самых известных примеров является AlphaFold. Коллектив обладал компетенциями в области биологии, физики, математики, алгоритмов глубокого обучения и оптимизации — то есть в области вычислительной биологии.
Работа была посвящена проблеме получения структуры белка, который бы отвечал заранее заданным свойства. Была обучена нейросеть, которая предсказывает расстояния и углы между атомами аминокислот в конечном белке, а также структуру белка в 3D-виде.
Допустим, вы решили заняться разработкой приложения для определения породы кошек. Как будет выглядеть план исследования?
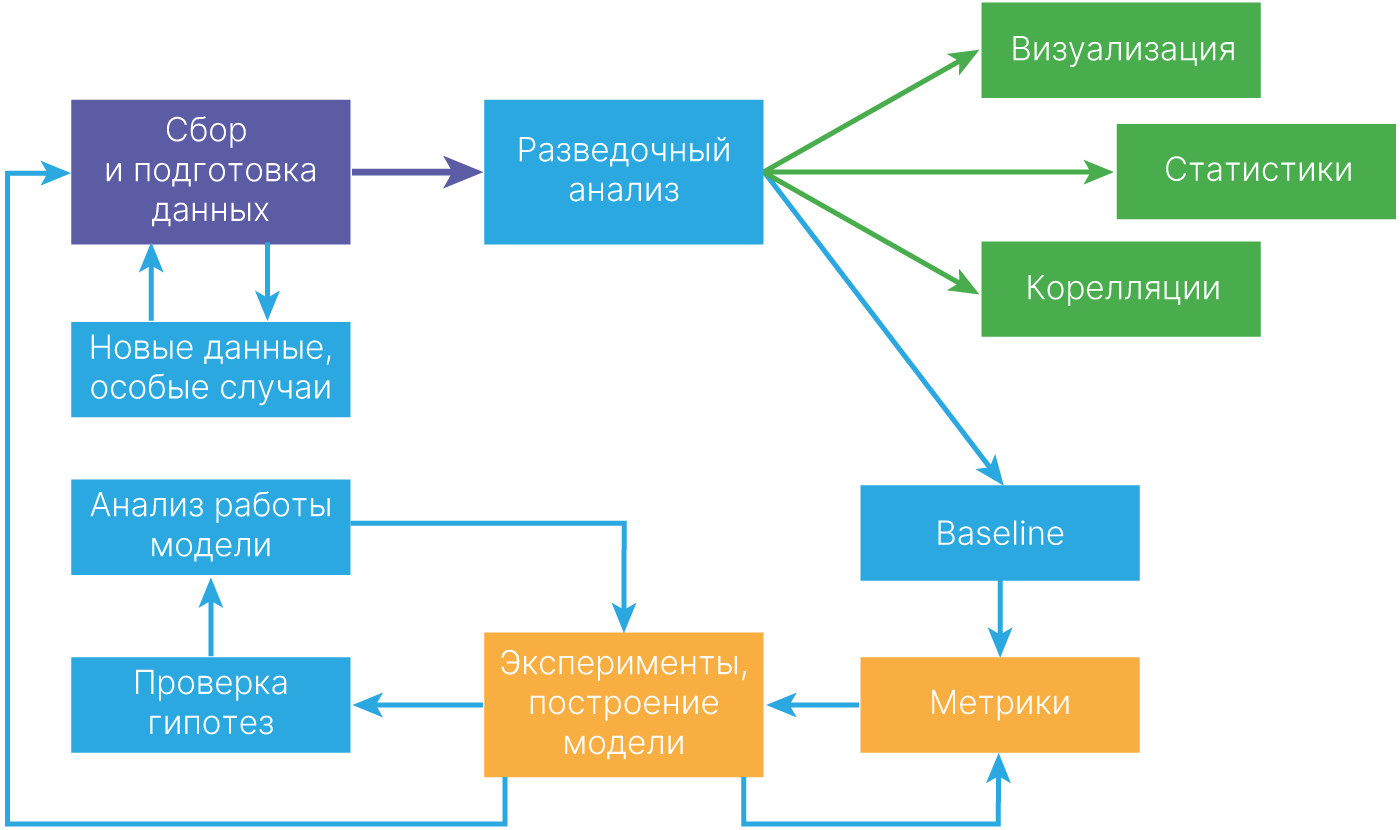
Где можно добыть данные?
Пройдитесь по соседним лабораториям. Напишите письма авторам статей.
Если вы используете данные, скачанные из сети, проверьте, откуда они. Описаны ли они в статье? Если да, посмотрите на документ; убедитесь, что он был опубликован в авторитетном месте, и проверьте, упоминают ли авторы какие-либо ограничения на использованные датасеты.
Если данные использовались в ряде работ, это еще не гарантирует высокое качество датасета. Иногда данные используются только потому, что их легко достать.
Даже широко распространённые датасеты могут иметь ошибки или какую-то странную специфику. Например, при исследовании ImageNet были обнаружены миллионы изображений темнокожих, которые были помечены как "преступник". В итоге большая часть набора данных ImageNet была удалена.

Существуют исследования 🎓[arxiv], которые связывают странное поведение современных нейронных сетей и ошибки в разметке.
Если вы обучаете свою модель на плохих данных, то, скорее всего, у вас получится плохое решение задачи. Существует соответствующий термин: garbage in, garbage out. Всегда начинайте с проверки данных.
Как будут выглядеть данные во время инференса модели?
Не окажется ли, что при обучении все кошки были мохнатые, а на инференсе попался сфинкс?

Что делать?
Подробнее с этим вы познакомитесь в ходе курса.
Exploratory data analysis, EDA — анализ основных свойств данных, нахождение в них общих закономерностей, распределений и аномалий, построение начальных моделей с использованием инструментов визуализации.
Подробнее с этим вы познакомитесь в следующих лекциях.
Примеры:
Постройте вашу первую систему быстро, а затем итерационно улучшайте.
Возьмите что-то простое, готовое. Ваша сложная модель должна работать не хуже.
Возможно, даже простая модель сможет решить вашу задачу с достаточным качеством.
Учтите нижнюю границу качества. За baseline можно считать известное значение. Например, результат работы классических методов или качество решения задачи человеком.
А как измерить это качество?
По ходу курса мы познакомимся с великим множеством метрик для различных задач. Важно, что любая из них должна быть выбрана заранее, до получения результатов.
Фактически вы оцениваете, какой показатель нужно улучшить и как этот показатель измерить.
Метрика должна отвечать целевой задаче.
Так, отличной метрикой при разработке генератора упражнений для изучения программирования может быть улучшение оценок слушателей на внешних экзаменах.
Обищй совет: используйте однопараметрические метрики.
Так, если у нас есть 2 классификатора, вводя две метрики, тяжело оценить, какой из них лучше — А или В.
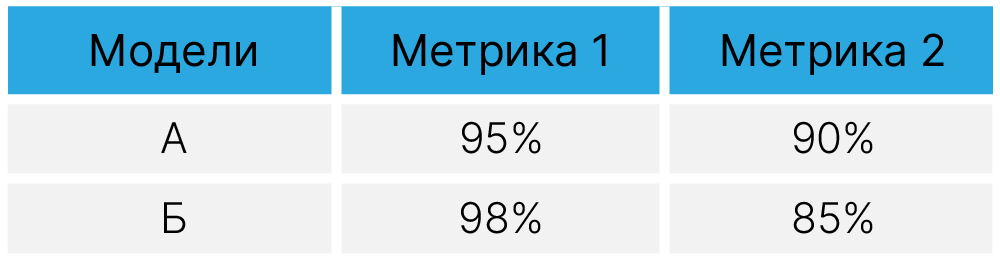
Но если эти метрики объединить в одну, провести сравнение будет гораздо проще.

Также не стоит забывать об оптимизационных метриках. Мы можем улучшать не только точность.
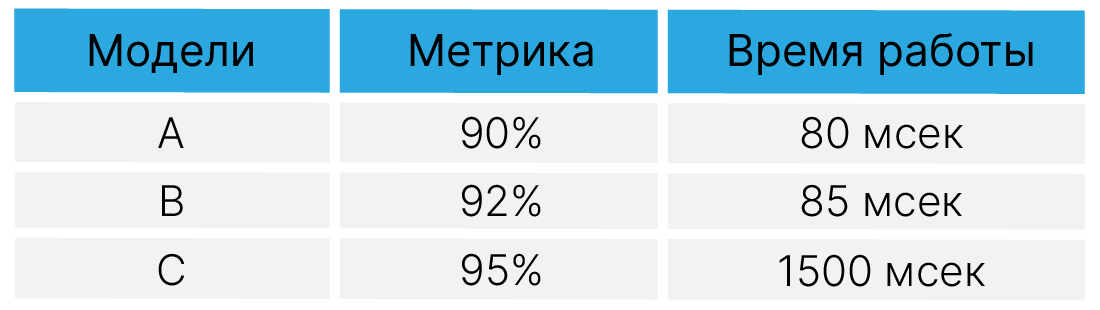
Заметьте, что метрика получается не однопараметрическая. Вместо введения формулы типа $$\large F_1 + 0,5*Скорость$$ можно сделать отсечку допустимого времени рассчётов и использовать точность в качестве целевой метрики среди оставшихся моделей.
По ходу курса мы будем не только писать модели с нуля, но и знакомиться с базами готовых моделей, в том числе предобученных. Таким образом, сразу логируйте результаты экспериментов. Подумайте, как вам это будет делать удобнее.
Смотрите на примеры из валидационной выборки, на которых есть ошибки. Так, разумным будет выделить 2 группы объектов:
Возьмите разумное количество объектов, которые можно проверить вручную (скажем, 100). Возможно, вы найдёте в этот момент ошибки в разметке или собак, которые очень похожи на котиков.
Результат анализа позволит понять, какой ожидаемый эффект будет от дальнейших действий. Если у вас окажется проблема с разметкой, улучшение алгоритма даст малый вклад.
Во время улучшения решения у вас будут появляться гипотезы, как можно улучшать решение. Имеет смысл при анализе ошибок завести подобную таблицу, в которой отмечать, на какие объекты в анализируемой подвыборке ожидается эффект.
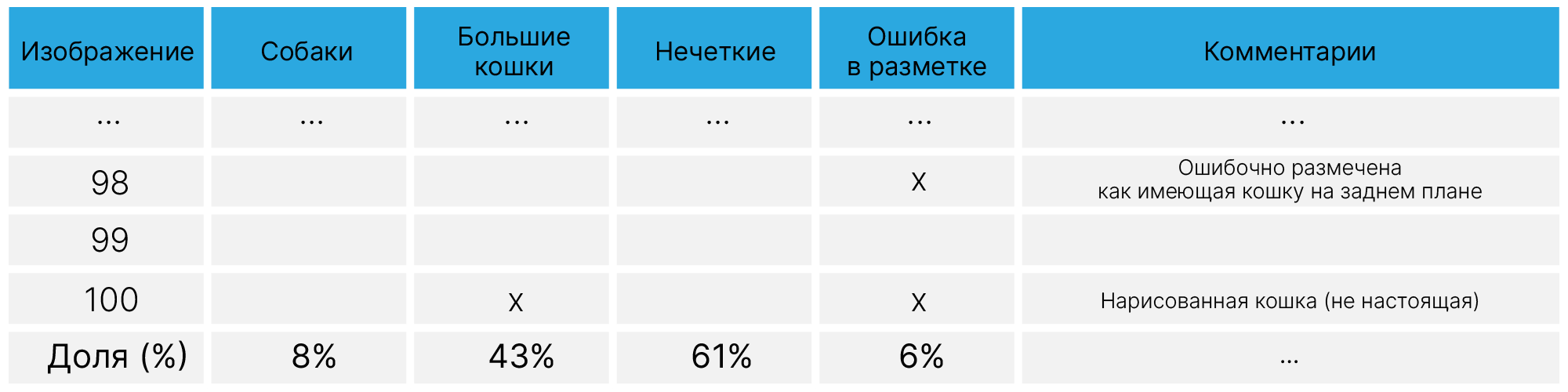
Таким образом можно оценить первоочередные улучшения.
После того, как модель готова, необходимо вскрыть "чёрный ящик". Об этом будет отдельная лекция.
Здесь вы сможете удостовериться, что модель выучила действительно значимые признаки, а не, например, фон.
Заметки от Эндрю Ына:
Рассмотрим примеры решения задач классификации на различных типах данных.
Будем использовать библиотеки:
[doc] 🛠️ Pandas — Удобная работа с табличными данными.
[doc] 🛠️ PyTorch — Основной фреймворк машинного обучения, который будет использоваться на протяжении всего курса.
[doc] 🛠️ Matplotlib — Основная библиотека для визуализации. Вывод различных графиков.
[doc] 🛠️ Seaborn — Удобная библиотека для визуализации статистик. Прямо из коробки вызываются и гистограммы, и тепловые карты, и визуализация статистик по датасету, и многое другое.
Существуют различные типы данных:
Последовательности (важен порядок данных, время):
Пространственно-структурированная информация (преобразуется к векторам чисел):
Статистика:
Большинство процессов и объектов, с которыми научились работать ML/DL модели, можно отнести к одному из перечисленных типов. Наша задача будет состоять в том, чтобы определить, как данные из вашей предметной области свести к одному из них и представить в виде набора чисел.
Для работы с различными типами данных используют разные типы моделей:
Табличный — классические ML модели либо полносвязные NN;
Последовательности — рекуррентные сети + свёртка;
Изображения/видео — 2,3 .. ND свёрточные сети.
В разных типах данных количество связей между элементами разное и зависит только от типа этих данных. Важно НЕ количество элементов, а СВЯЗИ между ними.

Данные мы можем условно делить по степени связанности. Это степень взаимного влияния между соседними элементами. Например, в таблице, в которой есть определенные параметры (например: рост, вес), данные между собой связаны, но порядок столбцов значения не имеет. Если мы поменяем столбцы местами, то не потеряем никакой важной информации.
Такие данные можно представить в виде вектора, но порядок элементов в нем не важен.
При работе с изображениями нам становится важно, как связаны между собой пиксели и по горизонтали, и по вертикали. При добавлении цвета появляются 3 RGB-канала, и значения в каждом канале также связаны между собой. Эту связь нельзя терять, если мы хотим корректно извлечь максимум информации из данных. Соответственно, если дано цветное изображение, то у нас есть уже три измерения, в которых мы должны эти связи учитывать.
Пример работы с табличными данными. Нам даётся описание вин из учебного датасета Wine 🛠️[doc].
Библиотека sklearn обеспечивает API по работе с датасетами, а также хранит ряд учебных. Посмотрим, как это выглядит.
Этот датасет можно загрузить, используя модуль sklearn.datasets библиотеки sklearn 🛠️[doc], чем мы и воспользуемся.
import sklearn
from sklearn.datasets import load_wine
dataset = load_wine(return_X_y=True)
# array 178x13 (178 wine examples each with 41 features)
features = dataset[0]
# array of 178 elements, each element is a number the class: 0,1 2
class_labels = dataset[1]
print("features shape:", features.shape)
print("class_labels shape:", class_labels.shape)
features shape: (178, 13) class_labels shape: (178,)
Выведем первый элемент массива. Это наш $X_1$ из множества наблюдений $X$. Обратите внимание на размер каждого элемента — это вектора из 13 признаков.
dataset[0][0:1]
array([[1.423e+01, 1.710e+00, 2.430e+00, 1.560e+01, 1.270e+02, 2.800e+00,
3.060e+00, 2.800e-01, 2.290e+00, 5.640e+00, 1.040e+00, 3.920e+00,
1.065e+03]])
А вот так выглядят первые 10 меток $Y$:
dataset[1][0:10]
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
Визуализация данных
Чтобы отобразить данные в виде таблицы, загрузим их в формате pandas.DataFrame.
В более крупных датасетах у вас могут появиться такие параметры, как доля загрузки датасета и фиксирование сида генератора случайных числе (для повторяемости загрузки).
# Import library to work with tabular data: https://pandas.pydata.org/
import pandas as pd
x, y = load_wine(return_X_y=True, as_frame=True)
x.head(3)
| alcohol | malic_acid | ash | alcalinity_of_ash | magnesium | total_phenols | flavanoids | nonflavanoid_phenols | proanthocyanins | color_intensity | hue | od280/od315_of_diluted_wines | proline | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 14.23 | 1.71 | 2.43 | 15.6 | 127.0 | 2.80 | 3.06 | 0.28 | 2.29 | 5.64 | 1.04 | 3.92 | 1065.0 |
| 1 | 13.20 | 1.78 | 2.14 | 11.2 | 100.0 | 2.65 | 2.76 | 0.26 | 1.28 | 4.38 | 1.05 | 3.40 | 1050.0 |
| 2 | 13.16 | 2.36 | 2.67 | 18.6 | 101.0 | 2.80 | 3.24 | 0.30 | 2.81 | 5.68 | 1.03 | 3.17 | 1185.0 |
А вот так мы можем посмотреть, какие уникальные классы в нашей выборке.
y.unique()
array([0, 1, 2])
Можно интерпретировать каждый объект как координаты точки в 13-мерном пространстве. Именно с таким представлением работает большинство алгоритмов машинного обучения.
Визуализируем распределение данных по классам и отметим, что присутствует дисбаланс.
import matplotlib.pyplot as plt
fig, axs = plt.subplots(figsize=(4, 3))
y.hist()
plt.suptitle("Label balance")
plt.show()
Предположим, что мы работаем с тренировочным датасетом CIFAR-10 🛠️[doc] и хотим решить хрестоматийную задачу классификации: определить те картинки из тестового набора данных, которые относятся к классу cat. Эта задача является частным примером общей задачи классификации данных CIFAR-10, разные подходы к решению которой мы ещё неоднократно рассмотрим в ходе курса.
Датасет CIFAR-10 содержит, как следует из названия, 10 различных классов изображений:

Все изображения представляют собой матрицы чисел, которые кодируют цвета отдельных пикселей. Для изображений высоты $H$, ширины $W$ с $C$ цветовыми каналами получаем упорядоченный набор $H \times W \times C$ чисел. В данном разделе пока не будем учитывать, что значения соседних пикселей изображения могут быть значительно связаны, и будем решать задачу классификации для наивного представления изображения в виде точки в $H \times W \times C$-мерном вещественном пространстве.
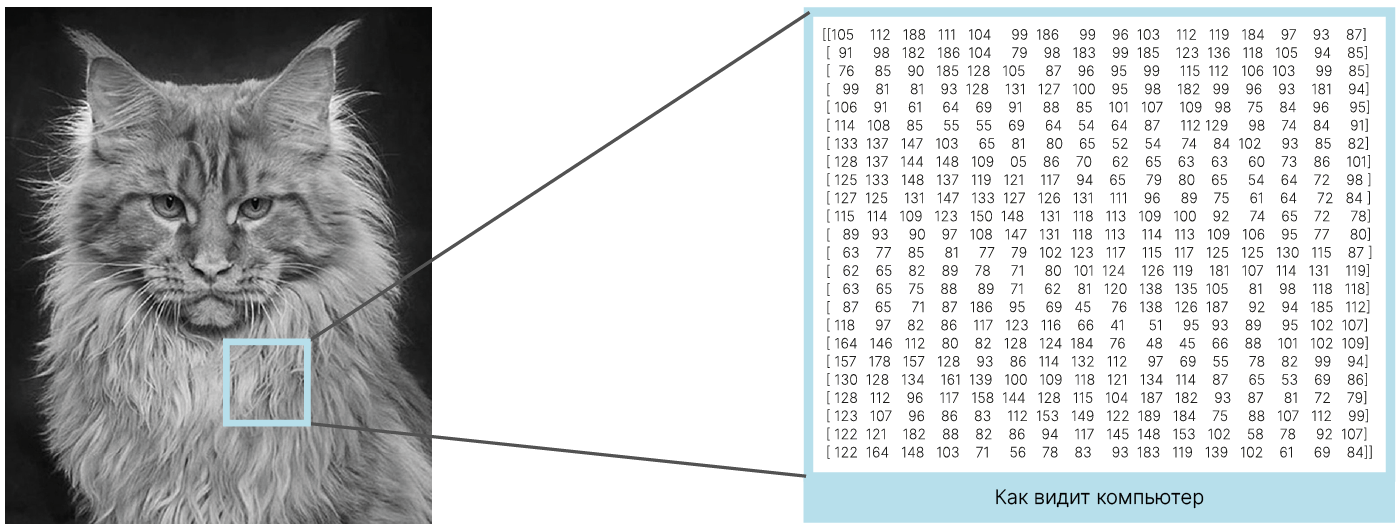
Датасет CIFAR-10 содержит цветные (трехцветные) изображения размером $32 \times 32$ пикселя. Таким образом, каждое изображение из датасета является точкой в $3072$-мерном ($32 \times 32 \times 3 = 3072$) вещественном пространстве.
Отметим, что помимо RGB встречаются и другие цветовые пространства ✏️[blog], которые однозначно (или приблизительно) переходят друг в друга.
Пара изображений будет выглядеть практически идентично, если значения цветов соответствующих пикселей будут похожи по величине. Другими словами, практически идентичным изображениям будут соответствовать близкие точки нашего многомерного вещественного пространства. Для численной характеристики близости можно определить функцию подсчета расстояния между парой точек — метрику.
Известны различные способы задания функции расстояния между парой точек 📚[wiki]). Простейшим примером является широко известная Евклидова ($L_2$) метрика: $$L_2 (X, Y) = \sqrt { \sum_i (X_i - Y_i)^2},$$
Но, кроме неё, величина расстояния между парой точек может быть выражена рядом других функций.
$L_1$-расстояние (манхэттенская метрика): $$L_1 (X, Y) = \sum_i |X_i - Y_i|,$$
угловое расстояние: $$\text{ang} (X, Y) = \frac{1}{\pi} \arccos \frac{\sum_i X_i Y_i}{\sqrt{\sum_i X_i^2} \sqrt{\sum_i Y_i^2}} ,$$
и многие другие. От выбора конкретной функции расстояния между точками будет явно зависеть представление о близости точек — объекты, близкие по одной из метрик, вовсе не обязаны оказаться близкими согласно другой.
Давайте попробуем вычислить $L_1$-расстояние между несколькими первыми изображениями из тестового набора данных CIFAR-10 с использованием реализованного в пакете sklearn 🛠️[doc] класса sklearn.metrics.DistanceMetric
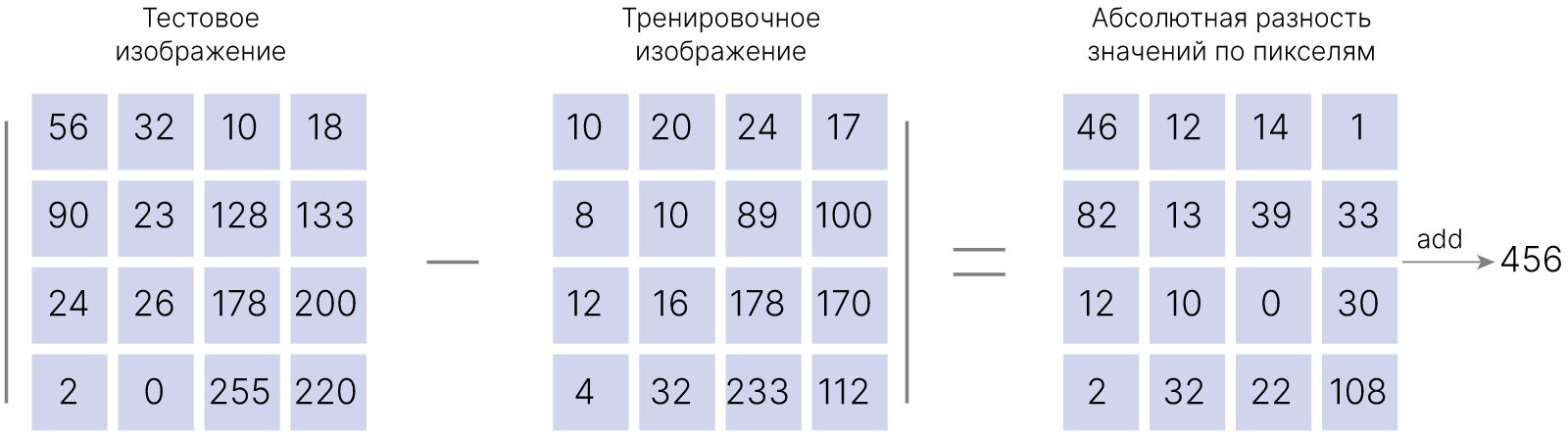
Загрузим данные:
# Load dataset from torchvision.datasets
from torchvision import datasets
train_set = datasets.CIFAR10("content", train=True, download=True)
val_set = datasets.CIFAR10("content", train=False, download=True)
labels_names = train_set.classes
Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to content/cifar-10-python.tar.gz
100%|██████████| 170498071/170498071 [00:03<00:00, 52644756.64it/s]
Extracting content/cifar-10-python.tar.gz to content Files already downloaded and verified
Выберем три изображения из тестового набора данных и одно из валидационного:
import matplotlib.pyplot as plt
img_1 = train_set.data[0]
img_2 = train_set.data[1]
img_3 = train_set.data[2]
fix, ax = plt.subplots(1, 3, figsize=(10, 3))
ax[0].set_title("First image in train data")
ax[0].imshow(img_1)
ax[1].set_title("Second image in train data")
ax[1].imshow(img_2)
ax[2].set_title("Third image in train data")
ax[2].imshow(img_3)
plt.show()
from sklearn.metrics import DistanceMetric
dist = DistanceMetric.get_metric("manhattan")
pairwise_dist = dist.pairwise([img_1.flatten(), img_2.flatten(), img_3.flatten()])
import numpy as np
fig, ax = plt.subplots(figsize=(4, 4))
im = ax.imshow(pairwise_dist)
# Show all ticks and label them with the respective list entries
ax.set_xticks(np.arange(len(pairwise_dist)))
ax.set_yticks(np.arange(len(pairwise_dist)))
ax.set_xticklabels([f"img{i}" for i in range(1, 4)])
ax.set_yticklabels([f"img{i}" for i in range(1, 4)])
# Rotate the tick labels and set their alignment.
plt.setp(ax.get_xticklabels(), rotation=45, ha="right", rotation_mode="anchor")
# Loop over data dimensions and create text annotations.
for i in range(len(pairwise_dist)):
for j in range(len(pairwise_dist)):
text = ax.text(
j,
i,
"{:0.2f}".format(pairwise_dist[i, j]),
ha="center",
va="center",
color="w",
)
ax.set_title("Pairwise L_1 distance for first 3 images in CIFAR 10 ")
fig.tight_layout()
plt.show()
Рассматривая аналогичные примеры, можно выявить, что расстояние между изображениями одного и того же класса может оказаться меньше, чем расстояние между объектами разных классов. Действительно, давайте рассчитаем среднее расстояние между объектами разных классов для CIFAR-10:
from sklearn.metrics.pairwise import manhattan_distances
# in order to limit computational time
index_limiter = 1000
# convert all (32,32,4) images into (32*32*4) vectors
flattened_images = val_set.data.reshape(val_set.data.shape[0], -1)[:index_limiter]
classwise_distance = np.zeros((len(val_set.classes), len(val_set.classes)))
# iterate over all pair of classes and slice their members
for class_id_i, class_name_i in enumerate(val_set.classes):
class_i_mask = np.asarray(val_set.targets[:index_limiter]) == class_id_i
for class_id_j, class_name_j in enumerate(val_set.classes):
class_j_mask = np.asarray(val_set.targets[:index_limiter]) == class_id_j
# manhattan_distances returns pairwise distance matrix for samples
# so in order to get mean distance for classes one should calc mean
# value over its higher triangle part or simply calc mean over whole matrix
# and divide by 2.0
classwise_distance[class_id_i, class_id_j] = (
np.mean(
manhattan_distances(
flattened_images[class_i_mask], flattened_images[class_j_mask]
)
)
/ 2.0
)
fig, ax = plt.subplots(figsize=(8, 8))
im = ax.imshow(classwise_distance)
# Show all ticks and label them with the respective list entries
ax.set_xticks(np.arange(len(val_set.classes)))
ax.set_yticks(np.arange(len(val_set.classes)))
ax.set_xticklabels(val_set.classes)
ax.set_yticklabels(val_set.classes)
# Rotate the tick labels and set their alignment.
plt.setp(ax.get_xticklabels(), rotation=45, ha="right", rotation_mode="anchor")
ax.set_title("Mean class-wise Мanhattan distance for CIFAR 10")
fig.tight_layout()
fig.colorbar(im)
plt.show()
Как мы видим, среди первых 1000 картинок тестовой части датасета CIFAR-10 есть значительное число обособленных классов, для которых выполняется описанное выше отношение близости. Например, это справедливо для классов "Корабль", "Олень" и "Лягушка". Идея о том, что близость объектов по некоторой метрике и их принадлежность к одному определённому классу связаны, является основой известного алгоритма классификации и регрессии — k-Nearest Neighbors.
Метод k-ближайших соседей 📚[wiki] (англ. k-nearest neighbors algorithm, k-NN) — метрический алгоритм для классификации или регрессии. В случае классификации алгоритм сводится к следующему:
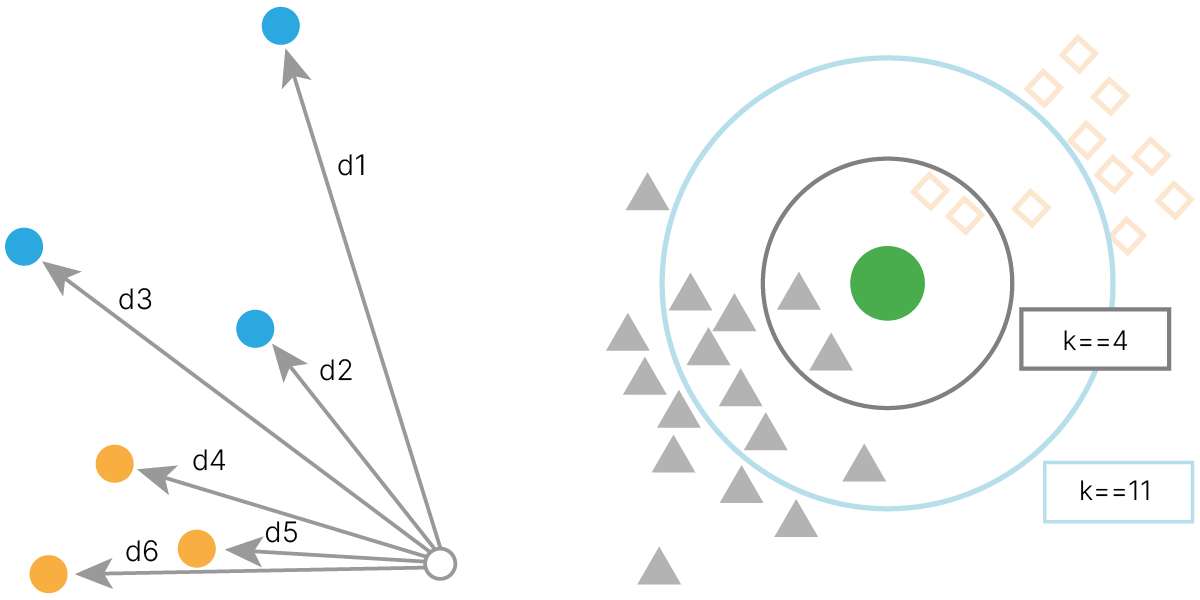
В качестве примера работы с алгоритмом k-NN классифицируем изображение корабля из тестовой выборки CIFAR-10 с использованием реализации алгоритма в scikit-learn 🛠️[doc].
fig, ax = plt.subplots(figsize=(3, 3))
sample_ship_img = val_set.data[18]
ax.set_title("Image in validation data")
plt.imshow(sample_ship_img)
plt.show()
Рассчитаем близость с валидационным изображением согласно трём распространённым расстояниям.
from sklearn.neighbors import KNeighborsClassifier
# in order to limit computational time
index_limiter = 5000
x = train_set.data.reshape(train_set.data.shape[0], -1)[:index_limiter]
y = train_set.targets[:index_limiter]
res = np.empty(shape=(3, 5), dtype=object)
i = 0
for distance_type in ["euclidean", "manhattan", "chebyshev"]:
for k in range(3, 7, 1):
knn = KNeighborsClassifier(n_neighbors=k, metric=distance_type)
knn.fit(x, y)
result_class_id = knn.predict([sample_ship_img.flatten()])[0]
result_class = train_set.classes[result_class_id]
res[i][0] = distance_type
res[i][k - 2] = result_class
i += 1
import pandas as pd
pandas_res = pd.DataFrame(res, columns=["distance", "k=3", "k=4", "k=5", "k=6"])
pandas_res.set_index("distance", inplace=True)
pandas_res
| k=3 | k=4 | k=5 | k=6 | |
|---|---|---|---|---|
| distance | ||||
| euclidean | automobile | ship | ship | ship |
| manhattan | automobile | automobile | truck | ship |
| chebyshev | ship | ship | ship | ship |
Как видим, при k=6 ответы совпадают при всех метриках. Но как выбрать k?
Довольно естественно оценивать долю правильных ответов алгоритма:
$$ \large \text{Accuracy} = \frac{P}{N}, $$где $P$ — количество верно предсказанных классов,
$\quad\ N$ — общее количество тестовых примеров.
Давайте наш алгоритм будет предсказывать как можно больше правильных классов!
from sklearn.metrics import accuracy_score
knn = KNeighborsClassifier(n_neighbors=6, metric="chebyshev")
knn.fit(x, y)
accuracy = accuracy_score(y_pred=knn.predict(x), y_true=y) # accuracy
print("Accuracy:", f"{accuracy*100}%")
Accuracy: 27.98%
Самым простым способом научиться чему-либо является "запомнить всё".
Вспомним "Таблицу умножения". Если мы хотим проверить умение умножать, то проверки примерами из таблицы умножения будет недостаточно, ведь она может быть полностью запомнена. Нужно давать новые примеры, которых не было в таблице умножения (обучающей выборке).
Если модель "запомнит всё", то она будет идеально работать на данных, которые мы ей показали, но может вообще не работать на любых других данных.
С практической точки зрения важно, как модель будет вести себя именно на незнакомых ей данных, то есть, насколько хорошо она научилась обобщать закономерности, которые в данных присутствовали (если они вообще существуют).
Для оценки этой способности набор данных разделяют на три части:

В sklearn.model_selection есть модель для разделения массива данных на тренировочную и тестовую часть.
from sklearn.model_selection import train_test_split
# split data to train/test
x_train, x_tmp, y_train, y_tmp = train_test_split(x, y, test_size=0.2)
x_val, x_test, y_val, y_test = train_test_split(x_tmp, y_tmp, test_size=0.2)
print("Train:", np.array(x_train).shape, np.array(y_train).shape)
print("Val:", np.array(x_val).shape, np.array(y_val).shape)
print("Test:", np.array(x_test).shape, np.array(y_test).shape)
print("Total:", np.array(x).shape, np.array(y).shape)
Train: (4000, 3072) (4000,) Val: (800, 3072) (800,) Test: (200, 3072) (200,) Total: (5000, 3072) (5000,)
knn = KNeighborsClassifier(n_neighbors=6, metric="chebyshev")
knn.fit(x_train, y_train)
accuracy_train = accuracy_score(y_pred=knn.predict(x_train), y_true=y_train)
accuracy_val = accuracy_score(y_pred=knn.predict(x_val), y_true=y_val)
accuracy_test = accuracy_score(y_pred=knn.predict(x_test), y_true=y_test)
print("Accuracy train:", f"{accuracy_train*100}%")
print("Accuracy val :", f"{accuracy_val*100}%")
print("Accuracy test :", f"{accuracy_test*100}%")
Accuracy train: 26.775% Accuracy val : 17.125% Accuracy test : 12.5%
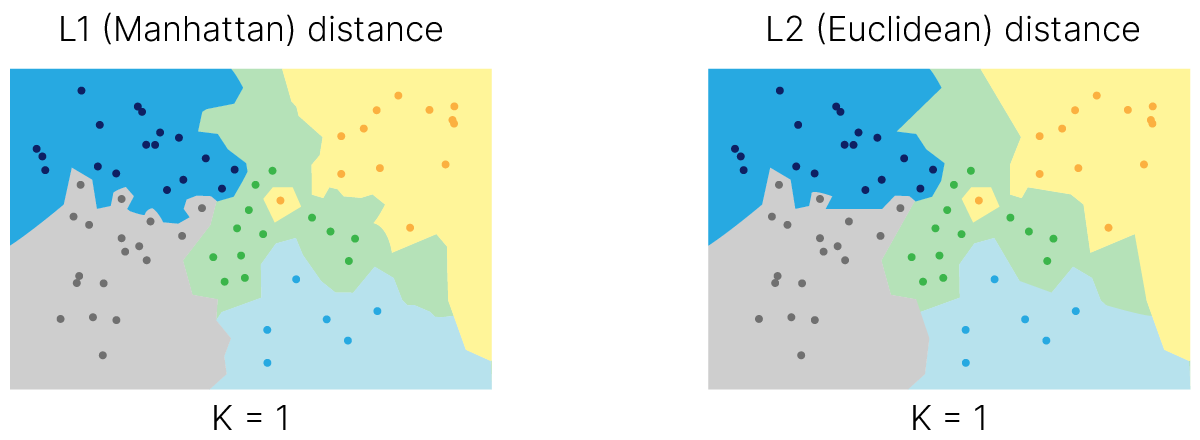
$\displaystyle L1 = d_1(I_1, I_2) = \sum_p|I^p_1-I^p_2| \qquad \qquad \quad L2 = d_2(I_1, I_2) = \sqrt{\sum_p(I^p_1-I^p_2)^2}$
Итого, у нас есть два параметра модели, которые мы можем настраивать:
Настраиваемые параметры, с помощью которых мы можем управлять процессом обучения, называются гиперпараметрами. В дальнейшем мы столкнемся с другими гиперпараметрами. Например, мы можем попробовать использовать другую модель, и выбор модели тоже станет гиперпараметром решаемой задачи.
Обучим k-NN для общей выборки данных при разном значении количества соседей.
num_neighbors = np.arange(1, 31) # array of the numbers of neighbors from 1 to 30
quality = np.zeros(num_neighbors.shape[0])
for i in range(num_neighbors.shape[0]): # for all elements
# create knn for all number of neighbors
knn = KNeighborsClassifier(n_neighbors=num_neighbors[i])
knn.fit(x_train, y_train)
q = accuracy_score(y_pred=knn.predict(x_train), y_true=y_train) # accuracy
quality[i] = q # fill quality
plt.figure(figsize=(8, 4))
plt.title("k-NN on train", size=18)
plt.xlabel("Neighbors", size=12)
plt.ylabel("Accuracy", size=12)
plt.plot(num_neighbors, quality)
plt.xticks(num_neighbors)
plt.show()
Видим, что качество на 1 соседе самое лучшее. Но это и понятно — ближайшим соседом элемента из обучающей выборки будет сам объект. Мы просто запомнили все объекты.
Если теперь мы попробуем взять какой-то новый объект и классифицировать его, у нас скорее всего ничего не получится. В таких случаях мы говорим, что наша модель не умеет обобщать (generalization).
Для того, чтобы знать заранее, обобщает ли наша модель или нет, мы можем разбить все имеющиеся у нас данныe на 2 части. На одной части мы будем обучать классификатор (train set), а на другой — тестировать, насколько хорошо он работает (test set).
num_neighbors = np.arange(
1, 31
) # array of the numbers of nearest neigbors from 1 to 30
train_quality = np.zeros(num_neighbors.shape[0]) # quality on train data
test_quality = np.zeros(num_neighbors.shape[0]) # quality on test data
for i in range(num_neighbors.shape[0]):
knn = KNeighborsClassifier(n_neighbors=num_neighbors[i])
knn.fit(x_train, y_train)
# accuracy on train data
train_quality[i] = accuracy_score(y_pred=knn.predict(x_train), y_true=y_train)
# accuracy on test data
test_quality[i] = accuracy_score(y_pred=knn.predict(x_test), y_true=y_test)
# accuracy plot on train and test data
plt.figure(figsize=(8, 4))
plt.title("k-NN on train vs test", size=18)
plt.plot(num_neighbors, train_quality, label="train")
plt.plot(num_neighbors, test_quality, label="test")
plt.legend()
plt.xticks(num_neighbors)
plt.xlabel("Neighbors", size=12)
plt.ylabel("Accuracy", size=12)
plt.show()
Вот, теперь мы видим, что 1 сосед был "ложной тревогой". Такие случаи мы называем переобучением. Чтобы действительно предсказывать что-то полезное, нам надо выбирать число соседей, начиная минимум с 3.
Метки классов в датасете могут быть распределены неравномерно. Для того, чтобы сохранить соотношение классов при разделении на train и test, необходимо указать параметр stratify при разбиении.
Еще одним параметром, используемым при разбиении, является shuffle (значение по умолчанию True). При shuffle = True датасет перед разбиением перемешивается.
Посмотрим на разбиение датасета Iris 🛠️[doc]. Для наглядности будем делить датасет пополам.
def count_lables(lables):
lable_count = {}
for item in lables:
if item not in lable_count:
lable_count[item] = 0
lable_count[item] += 1
return lable_count
def print_split_stat(x_train, x_test, y_train, y_test):
# print("Train labels: ", y_train)
# print("Test labels: ", y_test)
print("Train statistics: ", count_lables(y_train))
print("Test statistics: ", count_lables(y_test))
Посмотрим, как выглядит исходный датасет. Отметим, что объекты отсортированы. Ситуация вовсе не исключительная.
from sklearn.datasets import load_iris
data, labels = load_iris(return_X_y=True)
print("DataSet labels:\n", labels)
print("DataSet statistics: ", count_lables(labels))
DataSet labels:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
DataSet statistics: {0: 50, 1: 50, 2: 50}
Если мы выключим перемешивание (shuffle=False), то в обучение не попадёт ни один объект класса 2.
x_train, x_test, y_train, y_test = train_test_split(
data, labels, train_size=0.5, shuffle=False, random_state=42
)
print_split_stat(x_train, x_test, y_train, y_test)
Train statistics: {0: 50, 1: 25}
Test statistics: {1: 25, 2: 50}
По умолчанию shuffle=True, однако этого не достаточно. Доли объектов не равны в подвыборках.
x_train, x_test, y_train, y_test = train_test_split(
data, labels, train_size=0.5, random_state=42
)
print_split_stat(x_train, x_test, y_train, y_test)
Train statistics: {1: 27, 2: 27, 0: 21}
Test statistics: {1: 23, 0: 29, 2: 23}
Только при использовании стратификации мы добиваемся желаемого результата.
x_train, x_test, y_train, y_test = train_test_split(
data, labels, train_size=0.5, random_state=42, stratify=labels
)
print_split_stat(x_train, x_test, y_train, y_test)
Train statistics: {0: 25, 1: 25, 2: 25}
Test statistics: {0: 25, 2: 25, 1: 25}
В случае временных рядов, текстов и прочих данных, имеющих связь во времени, данные нельзя перемешивать. В таких задачах train должен предшествовать test по времени. Более подробно об этом будет рассказано в лекции про рекуррентные нейронные сети.
Можно иметь сколько угодно хороший алгоритм для классификации, но до тех пор, пока данные на входе — мусор, на выходе из классификатора мы тоже будем получать мусор (garbage in, garbage out). Давайте разберемся, что конкретно надо сделать, чтобы k-NN реально заработал.
Чтобы адекватно сравнить данные между собой, нам следует использовать нормализацию.
Нормализацией называется процедура приведения входных данных к единому масштабу (диапазону) значений.
Преобразование данных к единому числовому диапазону (иногда говорят домену) позволяет считать их равноправными признаками и единообразно передавать их на вход модели. В некоторых источниках данная процедура явно называется масштабирование.
Существует базовый вариант — StandardScaler.
Подробно рассмотрим различные виды нормализации в следующей лекции.
Как применять нормировку
Нельзя вычислять статистики на всём наборе данных, нормировать, а потом делить на подвыборки. Это ведёт к утечке данных и некорректным результатам.
from sklearn.preprocessing import StandardScaler
np.random.seed(42) # setting the initialization parameter for random values
x_train_feature = x_train[:, 0].reshape(-1, 1)
plt.figure(1, figsize=(8, 3))
plt.subplot(121) # set location
plt.scatter(x_train_feature, range(len(x_train_feature)), c=y_train)
plt.ylabel("Num examples", fontsize=15)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.title("Non scaled data", fontsize=18)
# scale data with StandardScaler
scaler = StandardScaler()
scaler.fit(x_train_feature)
x_train_feature_scaled = scaler.transform(x_train_feature)
plt.subplot(122)
plt.scatter(x_train_feature_scaled, range(len(x_train_feature)), c=y_train)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.title("StandardScaler", fontsize=18)
plt.show()
Идея StandardScaler заключается в том, что он преобразует данные таким образом, что распределение будет иметь среднее значение $0$ и стандартное отклонение $1$. Большинство значений будет находиться в диапазоне от $-1$ до $1$. Это стандартная трансформация, и она применима во многих ситуациях.
$u$ — среднее значение (или 0 при with_mean=False),
$s$ — стандартное отклонение (или 0 при with_std=False).
Обучим модель на данных без нормировки и с нормировкой для 10-ти соседей.
# split data to train/test
x_train, x_test, y_train, y_test = train_test_split(
data, labels, random_state=42, test_size=0.5
)
knn = KNeighborsClassifier(n_neighbors=10)
knn.fit(x_train, y_train)
print("Without normalization")
accuracy_train = accuracy_score(y_pred=knn.predict(x_train), y_true=y_train)
print("accuracy_train", round(accuracy_train, 3))
accuracy_test = accuracy_score(y_pred=knn.predict(x_test), y_true=y_test)
print("accuracy_test", round(accuracy_test, 3))
Without normalization accuracy_train 0.933 accuracy_test 0.947
scaler = StandardScaler()
scaler.fit(x_train)
x_train_norm = scaler.transform(x_train) # scaling data
x_test_norm = scaler.transform(x_test) # scaling data
knn = KNeighborsClassifier(n_neighbors=10)
knn.fit(x_train_norm, y_train)
print("With normalization")
accuracy_train = accuracy_score(y_pred=knn.predict(x_train_norm), y_true=y_train)
print("accuracy_train", round(accuracy_train, 3))
accuracy_test = accuracy_score(y_pred=knn.predict(x_test_norm), y_true=y_test)
print("accuracy_test", round(accuracy_test, 3))
With normalization accuracy_train 0.96 accuracy_test 0.973
На практике метод ближайших соседей для классификации используется редко. Проблема заключается в следующем.
Предположим, что точность классификации нас устраивает. Теперь давайте применим k-NN на больших данных (e.g. миллион картинок). Для определения класса каждой из картинок нам нужно сравнить ее со всеми другими картинками в базе данных, а такие расчеты, даже в существенно оптимизированном виде, занимают много времени. Мы же хотим, чтобы обученная модель работала быстро.
Тем не менее, метод ближайших соседей используется в других задачах, где без него обойтись сложно. Например, в задаче распознавания лиц. Представим, что у нас есть большая база данных с фотографиями лиц (например, по 5 разных фотографий всех сотрудников, которые работают в офисном здании) и есть камера, установленная на входе в это здание. Мы хотим узнать, кто и во сколько пришел на работу. Для того, чтобы понять, кто прошел перед камерой, нам нужно зафиксировать лицо этого человека и сравнить его со всеми фотографиями лиц в базе. В такой формулировке мы не пытаемся определить конкретный класс фотографии, а всего лишь определяем “похож-не похож”. Мы смотрим на k ближайших соседей, и если из k соседей, 5 — это фотографии, например, Джеки Чана, то, скорее всего, под камерой прошел именно он.
Примеры эффективной реализации метода на основе k-NN:
Давайте все-таки разберемся, как подобрать гиперпараметры.
Результат работы модели будет зависеть от разбиения. Поэкспериментируем с k-NN и датасетом Iris 🛠️[doc] и посмотрим, как результат работы модели зависит от random_state для train_test_split.
import numpy as np
import sklearn.datasets
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
dataset = sklearn.datasets.load_iris() # load data
x = dataset.data # features
y = dataset.target # labels(classes)
np.random.seed(42)
def split_and_train(x, y, random_state):
x_train, x_val, y_train, y_val = train_test_split(
x, y, train_size=0.8, stratify=y, random_state=random_state
)
max_neighbors = 30
num_neighbors = np.arange(1, max_neighbors + 1) # array of the number of neighbors
train_accuracy = np.zeros(max_neighbors)
val_accuracy = np.zeros(max_neighbors)
for k in num_neighbors:
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(x_train, y_train)
train_accuracy[k - 1] = accuracy_score(
y_pred=knn.predict(x_train), y_true=y_train
)
val_accuracy[k - 1] = accuracy_score(y_pred=knn.predict(x_val), y_true=y_val)
# accuracy plot on train and test data
plt.figure(figsize=(10, 4))
plt.title(f"KNN on train vs val, seed = {random_state}", size=20)
plt.plot(num_neighbors, train_accuracy, label="train")
plt.plot(num_neighbors, val_accuracy, label="val")
plt.legend()
plt.xticks(num_neighbors, size=12)
plt.xlabel("Neighbors", size=14)
plt.ylabel("Accuracy", size=14)
plt.show()
split_and_train(x, y, random_state=42)
split_and_train(x, y, random_state=4)
Результат зависит от того, как нам повезло или не повезло с разбиением данных на обучение и тест. Для одного разбиения хорошо выбрать $k=3$, а для другого — $k=13$. Кроме того, фактически мы сами выступаем в роли модели, которая учит гиперпараметры (а не параметры) под видимую ей выборку.
Получается, что если подбирать гиперпараметры модели на train set, то:
Для решения этой проблемы можно произвести несколько разбиений датасета на обучающий и валидационный по какой-то схеме, чтобы получить уверенность оценок качества для моделей с разными гиперпараметрами.
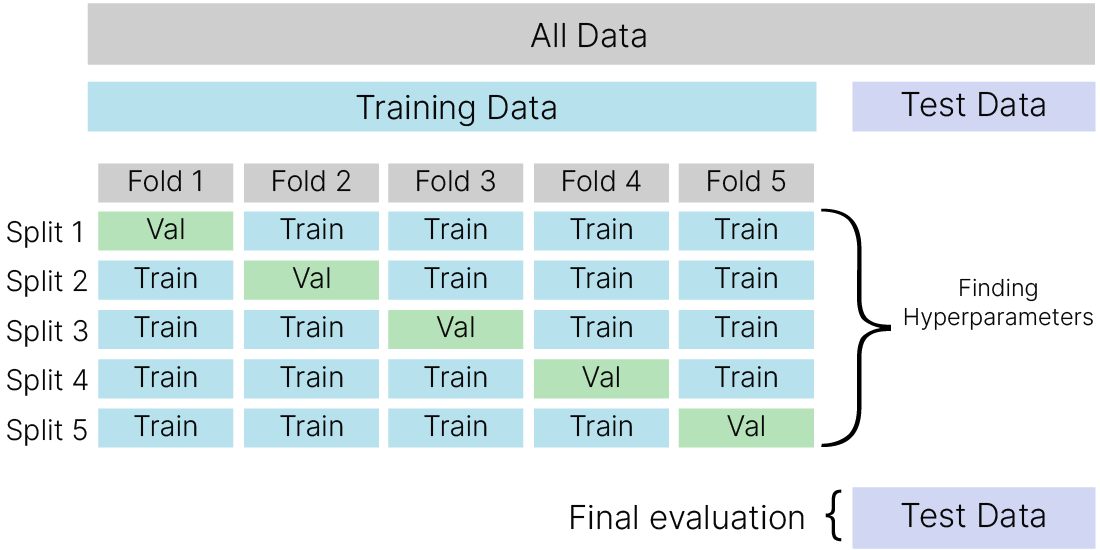
Такой подход называется K-Fold кросс-валидацией 🛠️[doc].
Берется тренировочная часть датасета, разбивается на части — блоки. Дальше мы будем использовать для проверки первую часть (Fold 1), а на остальных частях будем обучать модель. И так последовательно для всех частей. В результате у нас будет информация о точности для разных фрагментов данных, и уже на основании этого мы сможем понять, насколько значение параметра, который мы проверяем, зависит или не зависит от данных. То есть, если у нас от разбиения точность при одном и том же К меняться не будет, значит, мы подобрали правильный К. Если она будет сильно меняться в зависимости от того, на каком куске данных мы проводим тестирование, значит, надо попробовать другой К, и если ни при каком не получилось, то проблема заключается в данных.
Посмотрим, как работает k-Fold. Обратите внимание, что по умолчанию shuffle = False. Для упорядоченных данных это проблема.
from sklearn.model_selection import KFold
x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
print("index without shuffle")
kf = KFold(n_splits=3)
for train_index, test_index in kf.split(x):
print("TRAIN:", train_index, "TEST:", test_index)
print("index with shuffle")
kf = KFold(n_splits=3, random_state=42, shuffle=True)
for train_index, test_index in kf.split(x):
print("TRAIN:", train_index, "TEST:", test_index)
index without shuffle TRAIN: [3 4 5 6 7 8] TEST: [0 1 2] TRAIN: [0 1 2 6 7 8] TEST: [3 4 5] TRAIN: [0 1 2 3 4 5] TEST: [6 7 8] index with shuffle TRAIN: [0 2 3 4 6 8] TEST: [1 5 7] TRAIN: [1 3 4 5 6 7] TEST: [0 2 8] TRAIN: [0 1 2 5 7 8] TEST: [3 4 6]
Для получения стратифицированного разбиения (когда соотношение классов в частях разбиения сохраняется) нужно использовать StratifiedKFold 🛠️[doc].
Временные ряды
Отдельно нужно упомянуть о временных рядах. Особенностью таких данных является связность, наличие "настоящего", "прошедшего" и "будущего".
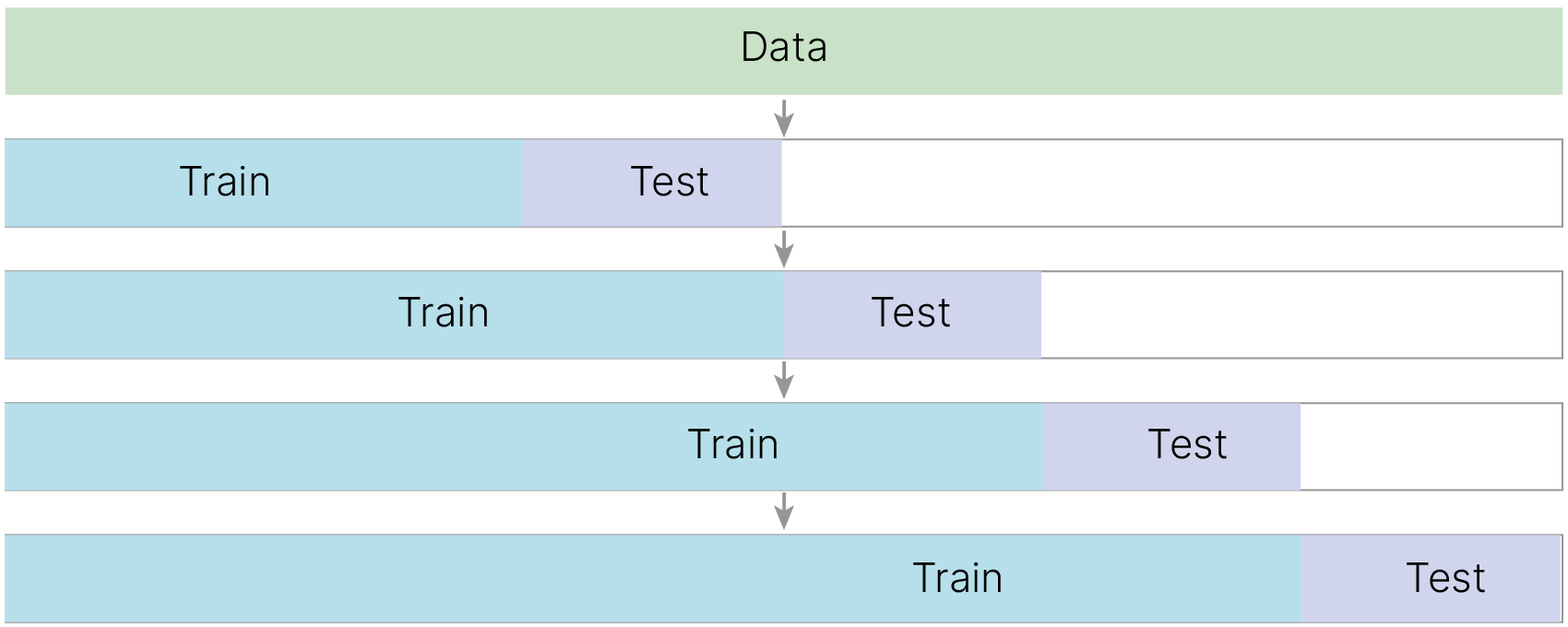
Посмотрим на результат кросс-валидации для k-NN.
from sklearn.model_selection import cross_val_score, StratifiedKFold
np.random.seed(42)
dataset = sklearn.datasets.load_iris() # load data
x = dataset.data # features
y = dataset.target # labels(classes)
x_train, x_test, y_train, y_test = train_test_split(
x, y, train_size=0.8, stratify=y, random_state=42
)
cv = StratifiedKFold(n_splits=5)
knn = KNeighborsClassifier(n_neighbors=3)
accuracy3 = cross_val_score(knn, x_train, y_train, cv=cv, scoring="accuracy")
knn = KNeighborsClassifier(n_neighbors=5)
accuracy5 = cross_val_score(knn, x_train, y_train, cv=cv, scoring="accuracy")
knn_cv = np.vstack(
(
np.hstack((accuracy3, accuracy3.mean(), accuracy3.std())),
np.hstack((accuracy5, accuracy5.mean(), accuracy5.std())),
)
)
import pandas as pd
table = pd.DataFrame(
knn_cv, columns=["Fold1", "Fold2", "Fold3", "Fold4", "Fold5", "Mean", "Std"]
)
table = table.set_axis(["Accuracy"] * 2)
table
| Fold1 | Fold2 | Fold3 | Fold4 | Fold5 | Mean | Std | |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.916667 | 0.958333 | 0.958333 | 0.958333 | 1.0 | 0.958333 | 0.026352 |
| Accuracy | 0.916667 | 1.000000 | 0.958333 | 1.000000 | 1.0 | 0.975000 | 0.033333 |
В идеальном случае выбираются гиперпараметры, для которых математическое ожидание метрик качества выше, а дисперсия меньше.
Можно ли делать только кросс-валидацию (без теста)?
Нет, нельзя. Кросс-валидация не до конца спасает от подгона параметров модели под выборку, на которой она проводится. Оценка конечного качества модели должно производиться на отложенной тестовой выборке. Если у вас очень мало данных, можно рассмотреть вложенную кросс-валидацию 🛠️[doc]. Речь об этом пойдет в следующих лекциях. Но даже в этом случае придется анализировать поведение модели, чтобы показать, что она учит что-то разумное. Кстати, вложенную кросс-валидацию можно использовать, чтобы просто получить более устойчивую оценку поведения модели на тесте.
Для подбора параметров модели используется GridSearchCV.
GridSearchCV – это инструмент для автоматического подбора параметров моделей машинного обучения. GridSearchCV находит наилучшие параметры путем обычного перебора: он создает модель для каждой возможной комбинации параметров из заданной сетки.
Датасет Iris маловат для подбора параметров, поэтому создадим свой датасет:
from sklearn.datasets import make_moons
x, y = make_moons(n_samples=1000, noise=0.3, random_state=42)
plt.figure(figsize=(10, 5))
plt.scatter(x[:, 0], x[:, 1], c=y)
plt.show()
Отложим test
x_train, x_test, y_train, y_test = train_test_split(
x, y, train_size=0.8, stratify=y, random_state=42
)
Попробуем подобрать параметры модели
from sklearn.model_selection import GridSearchCV
from warnings import simplefilter
simplefilter("ignore", category=RuntimeWarning)
"""
Parameters for GridSearchCV:
estimator — model
cv — num of fold to cross-validation splitting
param_grid — parameters names
scoring — metrics
n_jobs — number of jobs to run in parallel, -1 means using all processors.
"""
model = GridSearchCV(
estimator=KNeighborsClassifier(),
cv=KFold(5, shuffle=True, random_state=42),
param_grid={
"n_neighbors": np.arange(1, 31),
"metric": ["euclidean", "manhattan"],
"weights": ["uniform", "distance"],
},
scoring="accuracy",
n_jobs=-1,
)
model.fit(x_train, y_train)
GridSearchCV(cv=KFold(n_splits=5, random_state=42, shuffle=True),
estimator=KNeighborsClassifier(), n_jobs=-1,
param_grid={'metric': ['euclidean', 'manhattan'],
'n_neighbors': array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]),
'weights': ['uniform', 'distance']},
scoring='accuracy')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. GridSearchCV(cv=KFold(n_splits=5, random_state=42, shuffle=True),
estimator=KNeighborsClassifier(), n_jobs=-1,
param_grid={'metric': ['euclidean', 'manhattan'],
'n_neighbors': array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]),
'weights': ['uniform', 'distance']},
scoring='accuracy')KNeighborsClassifier()
KNeighborsClassifier()
Выведем лучшие гиперпараметры для модели, которые подобрали:
print("Metric:", model.best_params_["metric"])
print("Num neighbors:", model.best_params_["n_neighbors"])
print("Weigths:", model.best_params_["weights"])
Metric: euclidean Num neighbors: 30 Weigths: distance
Объект GridSearchCV можно использовать как обычную модель.
from sklearn.metrics import balanced_accuracy_score
y_pred = model.predict(x_test)
print(
f"Percent correct predictions {np.round(accuracy_score(y_pred=y_pred, y_true=y_test)*100,2)} %"
)
print(
f"Percent correct predictions(balanced classes) {np.round(balanced_accuracy_score(y_pred=y_pred, y_true=y_test)*100,2)} %"
)
Percent correct predictions 95.5 % Percent correct predictions(balanced classes) 95.5 %
Мы можем извлечь дополнительные данные о кросс-валидации и по ключу обратиться к результатам всех моделей:
list(model.cv_results_.keys())
['mean_fit_time', 'std_fit_time', 'mean_score_time', 'std_score_time', 'param_metric', 'param_n_neighbors', 'param_weights', 'params', 'split0_test_score', 'split1_test_score', 'split2_test_score', 'split3_test_score', 'split4_test_score', 'mean_test_score', 'std_test_score', 'rank_test_score']
Выведем для примера mean_test_score:
plt.figure(figsize=(14, 4))
plt.subplot(121)
plt.plot(model.cv_results_["mean_test_score"])
plt.title("Mean test score", size=20)
plt.xlabel("Num of experiment", size=15)
plt.ylabel("Accuracy", size=15)
plt.subplot(122)
plt.plot(model.cv_results_["param_metric"])
plt.title("Param Metric", size=20)
plt.xlabel("Num of experiment", size=15)
plt.show()
Построим, например, при фиксированных остальных параметрах (равных лучшим параметрам), качество модели на валидации в зависимости от числа соседей
selected_means = []
selected_std = []
num_neighbors = []
for ind, params in enumerate(model.cv_results_["params"]):
if (
params["metric"] == model.best_params_["metric"]
and params["weights"] == model.best_params_["weights"]
):
num_neighbors.append(params["n_neighbors"])
selected_means.append(model.cv_results_["mean_test_score"][ind])
selected_std.append(model.cv_results_["std_test_score"][ind])
Построим error bar для сравнения разброса ошибки при разном количестве соседей Neighbors.
Видим, что на самом деле большой разницы в числе соседей, начиная с 11, и нет.
plt.figure(figsize=(10, 4))
plt.title(f"KNN CV, {params['metric']}, {params['weights']}", size=18)
plt.errorbar(num_neighbors, selected_means, yerr=selected_std, fmt="-o")
plt.xticks(num_neighbors, size=13)
plt.ylabel("Mean_test_score", size=15)
plt.xlabel("Neighbors", size=15)
plt.show()
Альтернативой GridSearch является RandomizedSearch 🛠️[doc]. Если в GridSearch поиск параметров происходит по фиксированному списку значений, то RandomizedSearch умеет работать с непрерывными значениями, случайно выбирая тестируемые значения, что может привести к более точной настройке гиперпараметров.
Вы в явном виде указываете, сколько точек вы будете семплировать.
from sklearn.model_selection import RandomizedSearchCV
"""
Parameters for RandomizedSearchCV:
estimator — model
cv — num of fold to cross-validation splitting
param_distributions — parameters names
n_iter — number of parameter settings that are sampled. n_iter trades off runtime vs quality of the solution.
scoring — metrics
n_jobs — number of jobs to run in parallel, -1 means using all processors.
"""
model = RandomizedSearchCV(
estimator=KNeighborsClassifier(),
n_iter=100,
cv=KFold(5, shuffle=True, random_state=42),
param_distributions={
"n_neighbors": np.arange(1, 31),
"metric": ["euclidean", "manhattan"],
"weights": ["uniform", "distance"],
},
scoring="accuracy",
n_jobs=-1,
)
model.fit(x_train, y_train)
RandomizedSearchCV(cv=KFold(n_splits=5, random_state=42, shuffle=True),
estimator=KNeighborsClassifier(), n_iter=100, n_jobs=-1,
param_distributions={'metric': ['euclidean', 'manhattan'],
'n_neighbors': array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]),
'weights': ['uniform', 'distance']},
scoring='accuracy')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. RandomizedSearchCV(cv=KFold(n_splits=5, random_state=42, shuffle=True),
estimator=KNeighborsClassifier(), n_iter=100, n_jobs=-1,
param_distributions={'metric': ['euclidean', 'manhattan'],
'n_neighbors': array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]),
'weights': ['uniform', 'distance']},
scoring='accuracy')KNeighborsClassifier()
KNeighborsClassifier()
Выведем лучшие гиперпараметры для модели, которые подобрали:
print("Metric:", model.best_params_["metric"])
print("Num neighbors:", model.best_params_["n_neighbors"])
print("Weigths:", model.best_params_["weights"])
Metric: manhattan Num neighbors: 29 Weigths: distance
Как видим, параметры близки к выбранным полным перебором.
Объект RandomizedSearchCV также можно использовать как обычную модель.
y_pred = model.predict(x_test)
print(
f"Percent correct predictions {np.round(accuracy_score(y_pred=y_pred, y_true=y_test)*100,2)} %"
)
print(
f"Percent correct predictions(balanced classes) {np.round(balanced_accuracy_score(y_pred=y_pred, y_true=y_test)*100,2)} %"
)
Percent correct predictions 95.0 % Percent correct predictions(balanced classes) 95.0 %
Точность уменьшилась на 0.5%. Возможно, такое понижение вам не критично.
Насколько точна ваша модель?<img style: align="center" width="200" src ="https://edunet.kea.su/repo/EduNet-content/dev-2.0/L01/out/how_compute_model_accuracy.png">
Невозможно создать хорошее решение, не определив меру "хорошести". Нужно определиться с тем, как оценивать результат. Очень часто приходится слышать от заказчика вопрос со слайда. Чаще всего ответ “99%” их более чем устраивает.
Однако в большинстве случаев такой ответ приводит к проблемам. Почему?

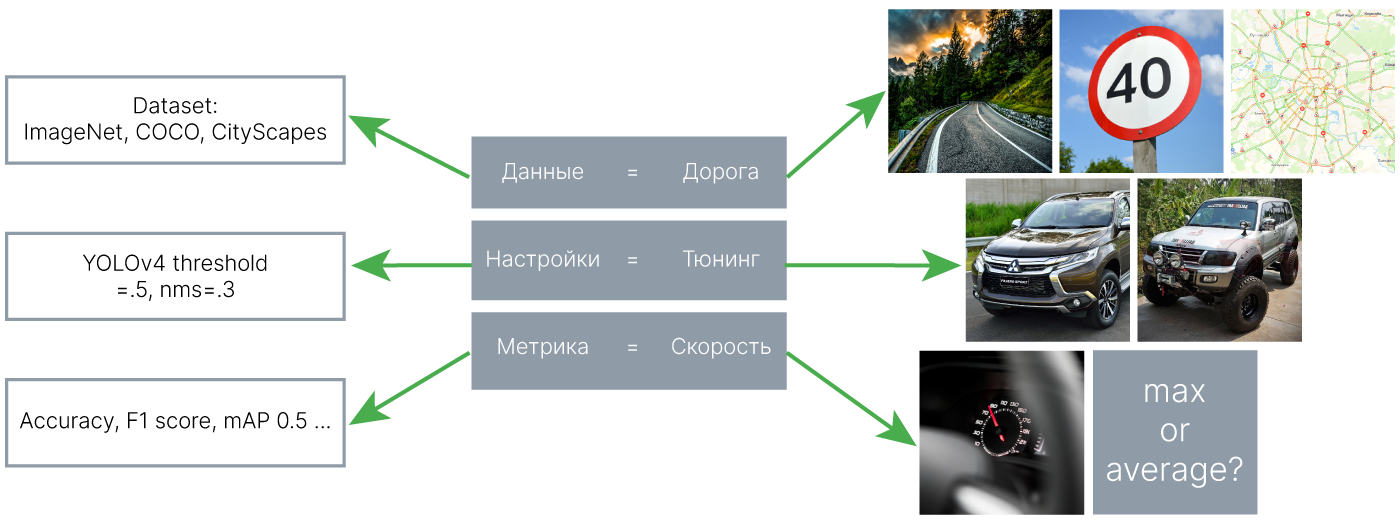
Всё это влияет на скорость перемещения, порой — радикально.
Также и точность наших моделей в первую очередь зависит от данных, на которых мы будем их оценивать. Модель, которая отлично работает на одном датасете, может намного хуже работать на другом или не работать вовсе.
Машина может быть подвергнута тюнингу. Например, внедорожный тюнинг поможет преодолеть участок бездорожья, на котором неподготовленный автомобиль застрянет. Но при этом скорость на дорогах общего пользования может снизиться. Также и модель, как правило, имеет ряд параметров (гиперпараметров), от которых зависит её работа. Они могут подбираться в зависимости от задачи (ошибки первого и второго рода) и качества данных.
Само понятие скорости допускает вариации: речь идет о средней или максимальной скорости? Аналогично и для оценки моделей существует несколько метрик, применение которых, опять же, зависит от целей заказчика и особенностей данных.
«На датасете X модель Y по метрике Z показала 99%».
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является уже знакомая нам accuracy — доля правильных ответов алгоритма.
$$ \large \text{Accuracy} = \frac{P}{N}, $$где $P$ — количество верно предсказанных классов,
$\quad\ N$ — общее количество тестовых примеров.
Какие есть недостатки у такого способа?

Accuracy нельзя использовать, если данные не сбалансированы, то есть в одном из классов больше представителей, чем в другом.
На рисунке выше мы видим, что при явном количественном преобладании объектов класса airplane модель может классифицировать все объекты как airplane и при этом получить такую же точность, как модель, которая учит все 3 класса, так как количество ошибок будет равно числу объектов классов, в которых меньше представителей (в данном случае в классах automobile и bird по 10 представителей, соответсвенно, 20 ошибок).
Также она не подойдет для задач сегментации и детектирования: если требуется не только определить наличие объекта на изображении, но и найти место, где он находится, то весьма желательно учитывать разницу в координатах.
Для решения этой проблемы вводятся метрики "точность" и "полнота"
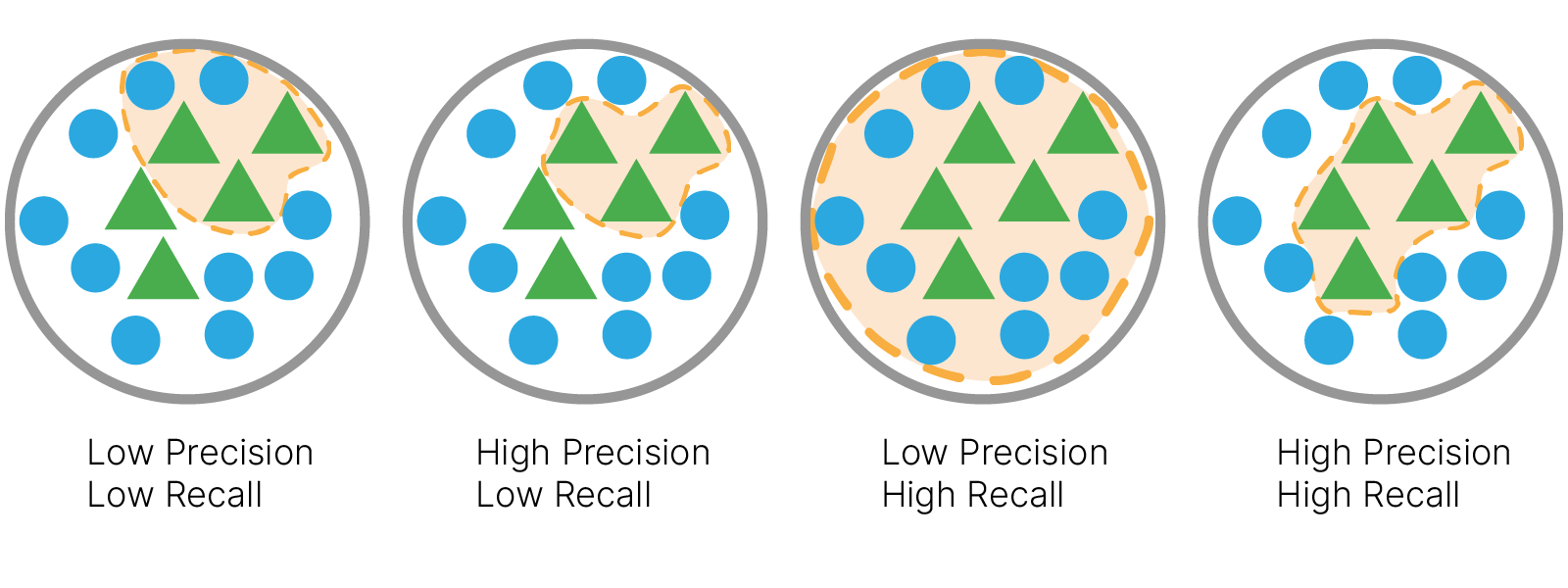
Для численного описания этих метрик необходимо ввести важную концепцию в терминах ошибок классификации — confusion matrix (матрица ошибок). Допустим, у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта к одному из классов. Тогда матрица ошибок классификации будет выглядеть следующим образом:
| $\large y=1$ | $\large y=0$ | |
|---|---|---|
| $\large \widehat{y}=1$ | $\large \text{True Positive} \ (TP) $ | $\large \text{False Positive} \ (FP) $ |
| $\large \widehat{y}=0$ | $\large \text{False Negative} \ (FN)$ | $\large \text{True Negative} \ (TN) $ |
Precision, recall
Для оценки качества работы алгоритма на каждом из классов по отдельности введем метрики precision (точность) и recall (полнота).
$\large \text{precision} = \frac{TP}{TP + FP}$
$\large \text{recall} = \frac{TP}{TP + FN}$
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive. Recall демонстрирует способность алгоритма обнаруживать данный класс вообще, а precision — способность отличать этот класс от других классов.
Accuracy
Accuracy также можно посчитать через матрицу ошибок.
$\text{Accuracy} = \dfrac{TP + TN}{TP + TN + FP + FN}$
Balanced accuracy
В случае дисбаланса классов есть специальный аналог точности – сбалансированная точность.
$\text{Balanced accuracy} = \dfrac{R_1 + R_0}{2} = \dfrac{1}{2} (\dfrac{TP}{TP + FN} + \dfrac{TN}{TN + FP})$
Для сбалансированного и несбалансированного случаев она будет равна $0. 96$ и $0.33$ соответственно.
Для простоты запоминания – это среднее полноты всех классов.
Ошибки классификации бывают двух видов: False Positive и False Negative. Первый вид ошибок называют ошибкой I-го рода, второй — ошибкой II-го рода. Пусть студент приходит на экзамен. Если он учил и знает, то принадлежит классу с меткой 1, иначе — имеет метку 0 (знающего студента называем «положительным»). Пусть экзаменатор выполняет роль классификатора: ставит зачёт (т.е. метку 1) или отправляет на пересдачу (метку 0). Самое желаемое для студента «не учил, но сдал» соответствует ошибке 1 рода, вторая возможная ошибка «учил, но не сдал» – 2 рода.

Часто в реальной практике стоит задача найти оптимальный баланс между Presicion и Recall. Классическим примером является задача определения оттока клиентов.
F-мера (в общем случае $\ F_\beta$) — среднее гармоническое precision и recall :
$\large \ F_\beta = (1 + \beta^2) \cdot \frac{\text{precision} \cdot \text{recall}}{(\beta^2 \cdot \text{precision}) + \text{recall}}$
$\beta$ в данном случае определяет вес точности в метрике, и при $\beta = 1$ это среднее гармоническое (в случае $\text{precision} = 1$ и $\text{recall} = 1$ получим $\ F_1 = 1$).
F-мера достигает максимума при полноте и точности, равными единице, и близка к нулю, если один из аргументов близок к нулю.
Сбалансированная F-мера, $β=1$:
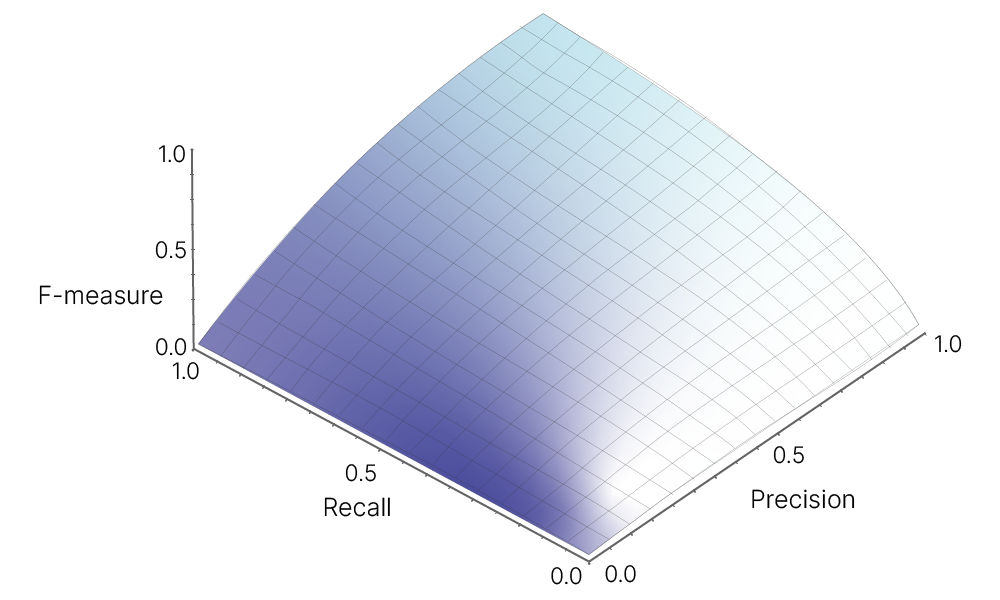
При перекосе в точность ($β=1/4$):
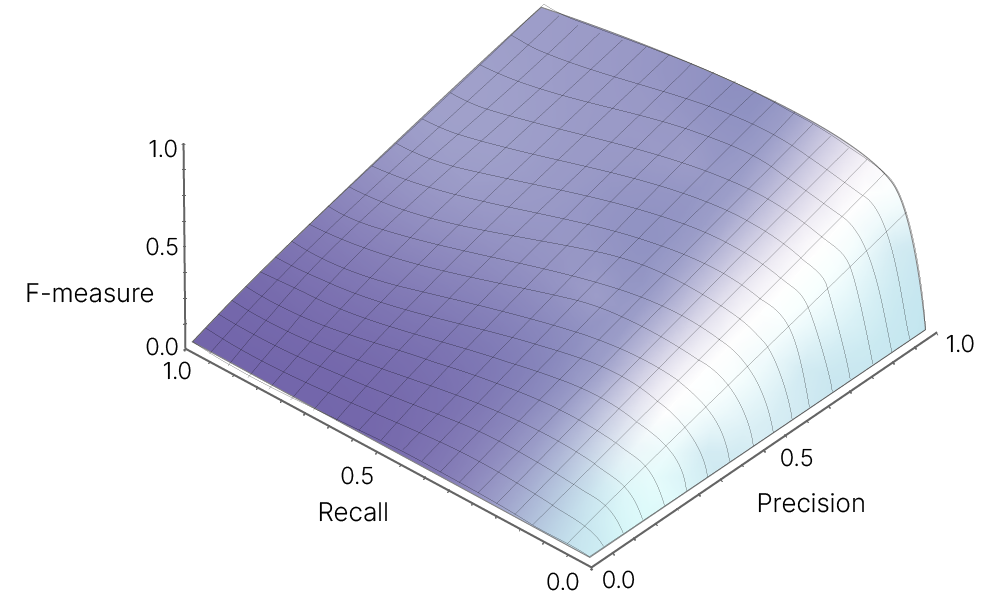
Более наглядно: низкие значения точности не позволяют метрике F вырасти.
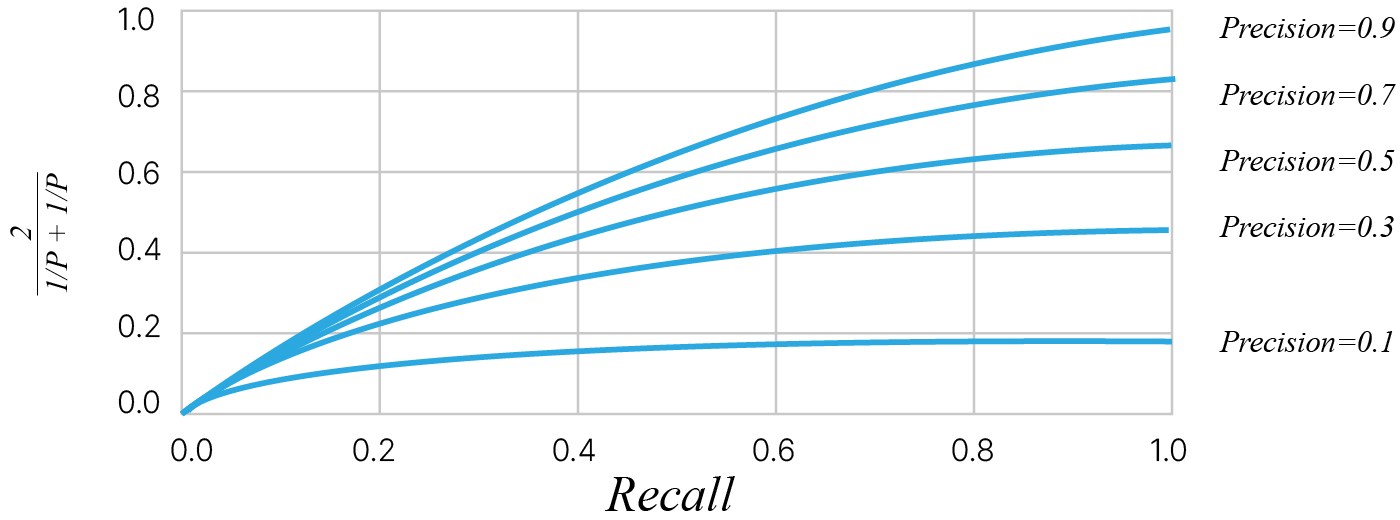
В sklearn есть удобная функция sklearn.metrics.classification_report, возвращающая recall, precision и F-меру для каждого из классов, а также количество экземпляров каждого класса.
from sklearn.metrics import classification_report
y_true = [0, 1, 2, 2, 2]
y_pred = [0, 0, 2, 2, 1]
target_names = ["class 0", "class 1", "class 2"]
print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.50 1.00 0.67 1
class 1 0.00 0.00 0.00 1
class 2 1.00 0.67 0.80 3
accuracy 0.60 5
macro avg 0.50 0.56 0.49 5
weighted avg 0.70 0.60 0.61 5
Многоклассовый случай
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
fig.tight_layout(pad=3.0)
plt.rcParams.update({"font.size": 16})
# font = {'size':'21'}
ax[0].set_title("Balanced data")
ax[1].set_title("Unbalanced data")
labels = ["Airplane", "Auto", "Bird"]
# Balanced data
air, auto, bird = 150, 150, 150
actual_b = np.array([0] * air + [1] * auto + [2] * bird)
predicted_b = np.array([0] * (air - 10) + [1] * (auto + 20) + [2] * (bird - 10))
# Unbalanced data
air, auto, bird = 430, 10, 10
actual_ub = np.array([0] * air + [1] * auto + [2] * bird)
predicted_ub = np.array([0] * (air + 20) + [1] * (auto - 10) + [2] * (bird - 10))
metrics.ConfusionMatrixDisplay(
confusion_matrix=metrics.confusion_matrix(actual_b, predicted_b),
display_labels=labels,
).plot(ax=ax[0])
metrics.ConfusionMatrixDisplay(
confusion_matrix=metrics.confusion_matrix(actual_ub, predicted_ub),
display_labels=labels,
).plot(ax=ax[1])
label_font = {"size": "15"} # Adjust to fit
ax[0].set_xlabel("Predicted labels", fontdict=label_font)
ax[0].set_ylabel("True labels", fontdict=label_font)
ax[1].set_xlabel("Predicted labels", fontdict=label_font)
ax[1].set_ylabel("True labels", fontdict=label_font)
plt.show()
print(
"Accuracy Balanced Data:", round(metrics.accuracy_score(actual_b, predicted_b), 2)
)
print(
"Accuracy Unbalanced Data:",
round(metrics.accuracy_score(actual_ub, predicted_ub), 2),
)
Accuracy Balanced Data: 0.96 Accuracy Unbalanced Data: 0.96
print(
"Balanced accuracy for Balanced data :",
round(metrics.balanced_accuracy_score(actual_b, predicted_b), 2),
)
print(
"Balanced accuracy for Unbalanced data :",
round(metrics.balanced_accuracy_score(actual_ub, predicted_ub), 2),
)
Balanced accuracy for Balanced data : 0.96 Balanced accuracy for Unbalanced data : 0.33
Multiclass Accuracy
В случае многоклассовой классификации термины TP, FP, TN, FN считаются для каждого класса:
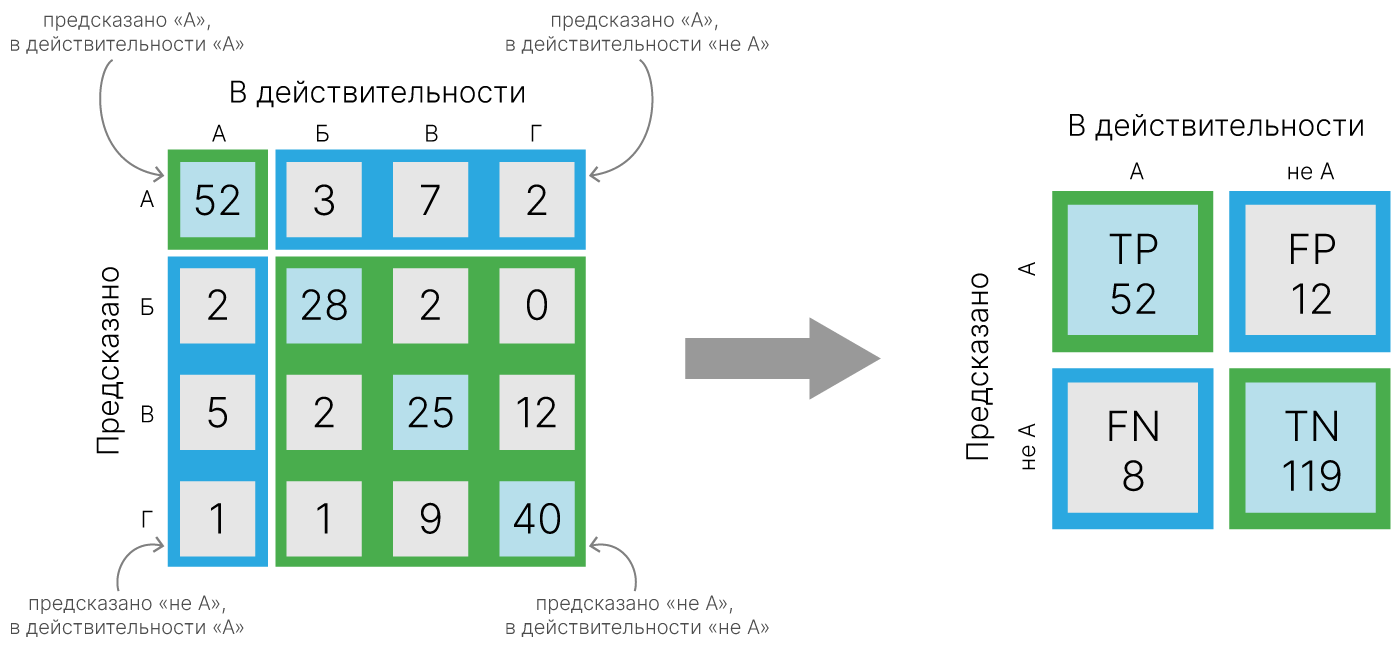
$\large \displaystyle \text{Multiclass Accuracy} = \frac{1}{n}\sum_{i=1}^{n} [\text{actual}_{i} == \text{predicted}_{i}] = \frac{\sum_{k=1}^{N} TP_{Ck} }{\sum_{k=1}^{N} (TP_{Ck} + TN_{Ck} + FP_{Ck} + FN_{Ck})}$
Пусть решается задача бинарной классификации, и необходимо оценить важность признака $j$ для решения именно этой задачи. В этом случае можно попробовать построить классификатор, который использует лишь этот один признак $j$, и оценить его качество. Например, можно рассмотреть очень простой классификатор, который берёт значение признака $j$ на объекте, сравнивает его с порогом $t$, и если значение больше этого порога, то он относит объект к первому классу, если же меньше порога, то к другому, нулевому или минус первому, в зависимости от того, как мы его обозначили. Далее, поскольку этот классификатор зависит от порога $t$, то его качество можно измерить с помощью таких метрик, как площадь под ROC-кривой или Precision-Recall кривой, а затем по данной площади отсортировать все признаки и выбрать лучшие.
Но вначале разберёмся, что такое AUC-ROC.
ROC-кривой (ROC, receiver operating characteristic, кривой ошибок) традиционно называют график кривой, которая характеризует качество предсказаний бинарного классификатора на некоторой фиксированной выборке при всех значениях порога классификации. Площадь под графиком ROC-кривой AUC (area under the curve) является численной характеристикой качества классификатора. Определим, как именно строится ROC-кривая, через рассмотрение примера.
Вывод некоторого бинарного классификатора представлен в табл. 1. Упорядочим строки данной таблицы по убыванию значения вывода нашего бинарного классификатора и запишем результат в табл. 2. Если наш алгоритм справился с задачей классификации, то мы увидим в последней колонке также упорядоченные по убыванию значения (или случайное распределение меток $0$ и $1$ в противном случае).
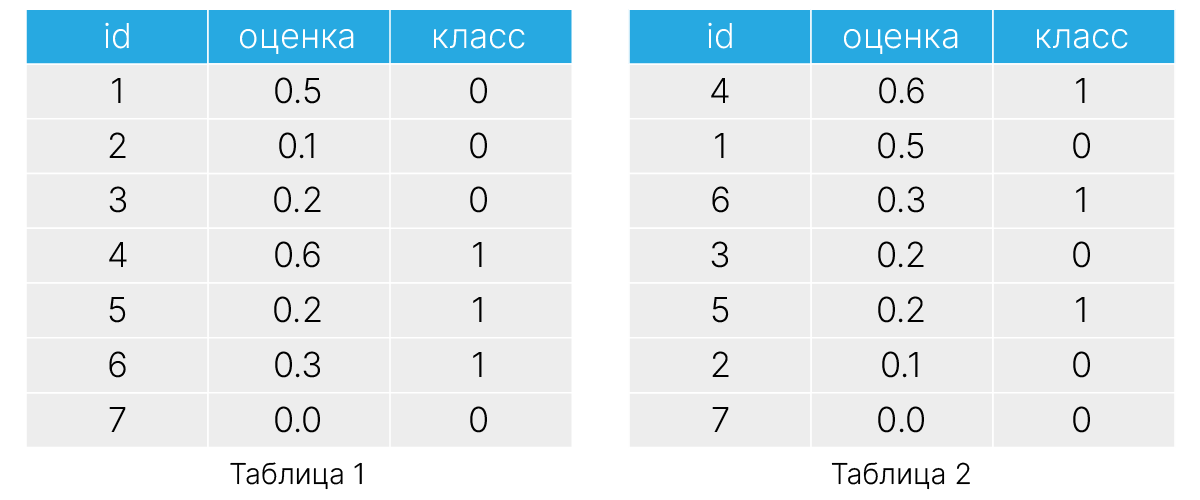
Приступим непосредственно к изображению графика ROC-кривой. Начнём с квадрата единичной площади и изобразим на нём прямоугольную координатную сетку, равномерно нанеся $m$ горизонтальных линий и $n$ вертикальных. Число горизонтальных линий $m$ соответствует количеству объектов класса $1$ из рассматриваемой выборки, а число $n$ — количеству объектов класса $0$. В нашем примере $m=3$ и $n=4$. Таким образом, квадрат единичной площади разбился на $m \times n$ прямоугольных блоков (на $12$ штук согласно нашему примеру).
Начиная из точки $(0, 0)$, построим ломаную линию в точку $(1, 1)$ по узлам получившейся решетки по следующему алгоритму:
(всего потребуется не более $n + m$ шагов — столько же, сколько строк в нашей таблице)
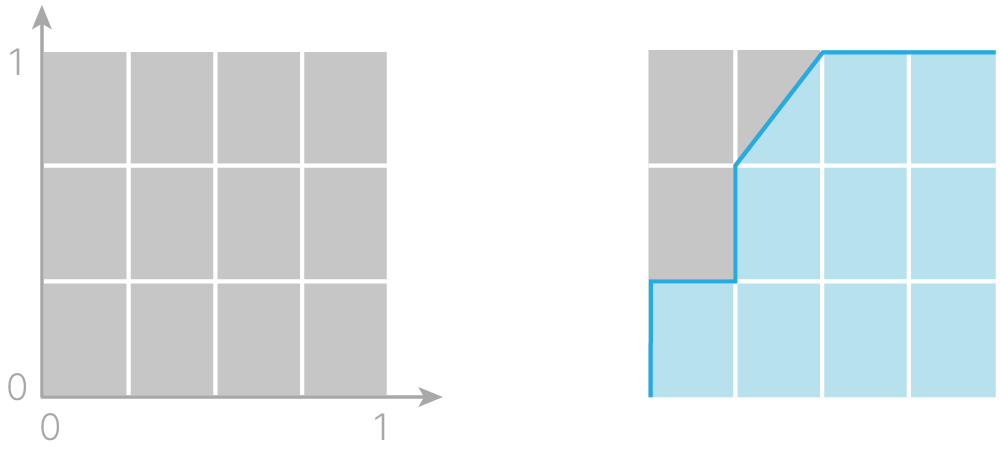
Справа на рис. 1 показана полученная для нашего примера кривая – эта изображенная на единичном квадрате ломаная линия и называется ROC-кривой.
Вычислим площадь под получившийся кривой — AUC-ROC. В нашем примере AUC-ROC $= 9.5 / 12 ~ 0.79$, и именно это значение является искомой метрикой качества работы нашего бинарного классификатора. (Так как мы начали свое построение с квадрата единичной площади, то AUC-ROC может принимать значения в $[0,1]$).

Как можно заметить на рис. 3, координатная сетка, описанная в нашем алгоритме построения ROC кривой, разбила единичный квадрат на столько прямоугольников, сколько существовало пар объектов класс-$0$ — класс-$1$ в исследуемой выборке данных. Если теперь посчитать количество оказавшихся под ROC-кривой прямоугольников, то можно заметить, что оно в точности равно числу верно классифицированных алгоритмом пар объектов, то есть таких пар объектов противоположных классов, для которых алгоритм поставил большую по величине оценку для объекта класса $1$.
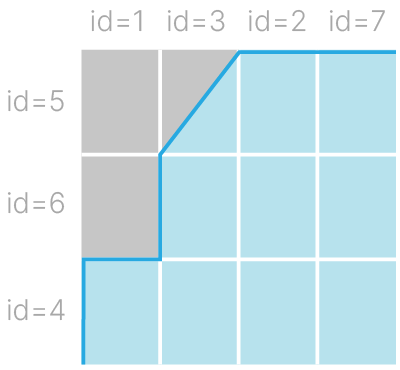
Таким образом, ROC-AUC равен части верно упорядоченных оценкой классификатора пар объектов противоположных классов (в которой объект класса $0$ получил оценку исследуемым классификатором ниже, чем объект класса $1$).
Есть ещё один случай — когда объект может принадлежать одновременно нескольким классам — называется multilabel (многометочная) классификация. Такую задачу не стоит сводить к задаче бинарной классификации по каждому классу, ибо метки могут быть не независимыми.
Допустим, у нас есть 3 объекта, и модель предсказала нам 3 набора меток.
# fmt: off
y_true = [[0,1,1,1],
[0,0,1,0],
[1,1,0,0]]
y_pred = [[0,1,0,1],
[0,1,1,1],
[1,0,1,1]]
# fmt: on
Accuracy
Оценивает точное совпадение векторов классов. Вариант — считать точность по каждому классу независимо.
Confusin Matrix
Специальная функция, которая создаст 4 матрицы, по одной на каждый класс.
from sklearn.metrics import multilabel_confusion_matrix
multilabel_confusion_matrix(y_true, y_pred)
array([[[2, 0],
[0, 1]],
[[0, 1],
[1, 1]],
[[0, 1],
[1, 1]],
[[0, 2],
[0, 1]]])
Precision, Recall, F1
Могут применяться независимо к каждой метке, также эти результаты можно объединить различными усреднениями:
Classification report
Может быть использован вами ровно так же, как и раньше.
from sklearn.metrics import classification_report
label_names = ["label A", "label B", "label C", "label D"]
print(classification_report(y_true, y_pred, target_names=label_names))
precision recall f1-score support
label A 1.00 1.00 1.00 1
label B 0.50 0.50 0.50 2
label C 0.50 0.50 0.50 2
label D 0.33 1.00 0.50 1
micro avg 0.50 0.67 0.57 6
macro avg 0.58 0.75 0.62 6
weighted avg 0.56 0.67 0.58 6
samples avg 0.56 0.72 0.57 6
Литература
Полезное:
Данные:
Руководства:
[git] 🐾 Три блокнота с подробным анализом реального датасета
[blog] ✏️ Как избежать «подводных камней» машинного обучения: руководство для академических исследователей — гайд по типичным ошибкам
Инструменты:
[doc] 🛠️ Pandas — табличные данные.
[doc] 🛠️ PyTorch — нейросети.
[doc] 🛠️ Matplotlib — визуализация.
[doc] 🛠️ Seaborn — визуализация статистик
Методы и алгоритмы:
Другое: