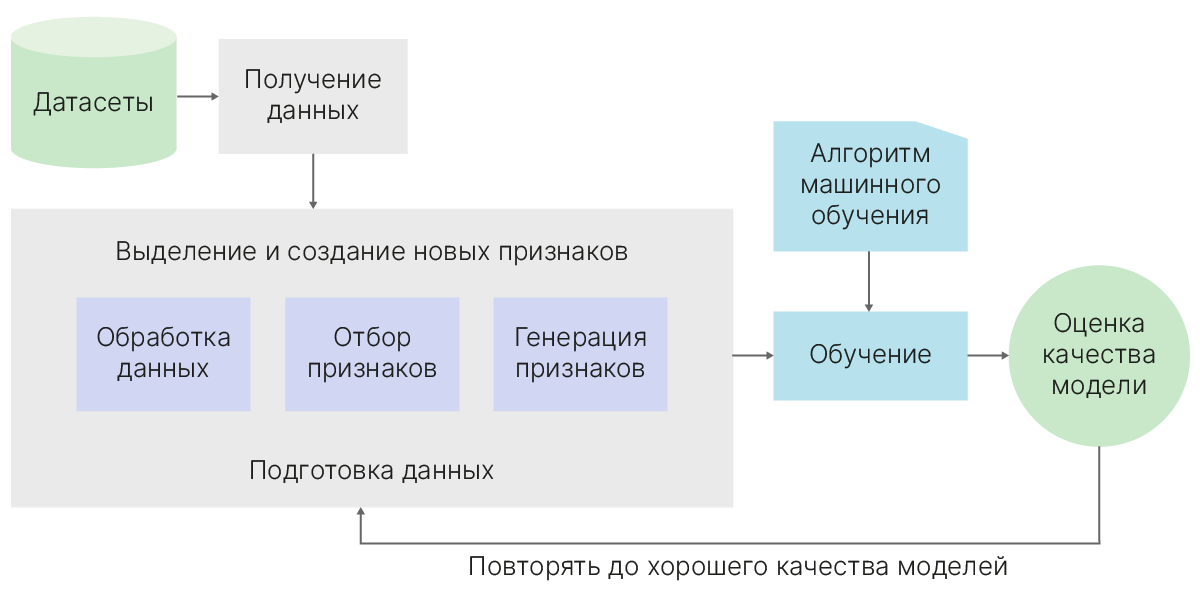
Генерация и отбор признаков
Coming up with features is difficult, time-consuming, requires expert knowledge. "Applied machine" learning is basically feature engineering. @Andrew Ng
Общая схема классического машинного обучения выглядит так. Даже в случае нейросетей некая предобработка исходных данных все равно не бывает лишней.

Feature engineering is the process of transforming raw data into features that better represent the underlying problem to the predictive models, resulting in improved model accuracy on unseen data. @Dr. Jason Brownlee
Генерация признаков — процесс придумывания способов описания данных с помощью простых значений, которые должны отражать характеристики объектов исследований, через которые выражаются целевые значения.
Изначально объекты в нашем датасете могут быть представлены в виде описаний, которые не являются признаковыми или требуют некоторой предобработки. Например:
Большая часть моделей не способна работать с такими представлениями в сыром виде и просто не запустится или будет выдавать неадекватные результаты.
Процесс создания признаков зависит от модели, которую мы собираемся использовать. Для одних моделей полезно добавить признаки, полученные делением/перемножением исходных. Другие модели могут провести эти операции сами, причем, экономнее/менее переобучаясь. Как вариант, добавление признаков, явно зависящих друг от друга, может даже мешать некоторым моделям.
Например, плохая идея добавлять в обычную линейную модель как признаки X1 и X2, так и их сумму.
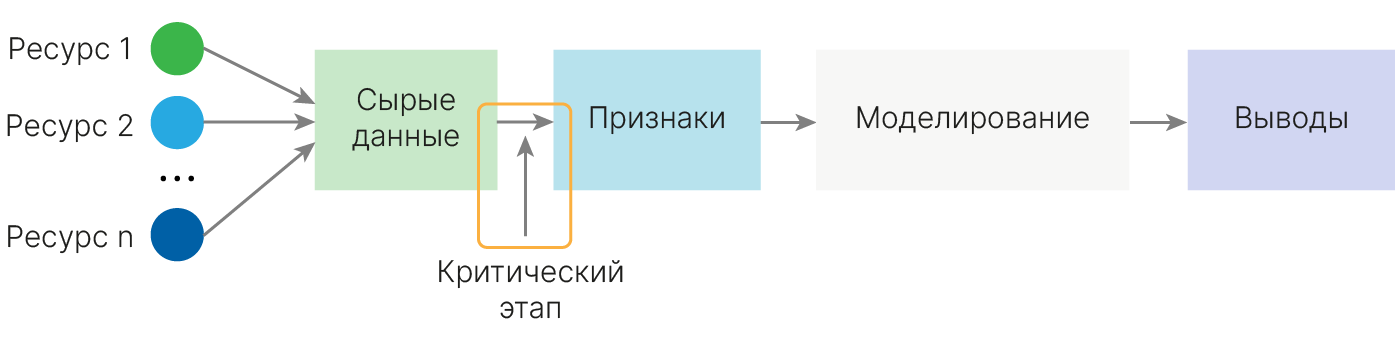
Вообще говоря, надо понимать, что процесс feature engineering является критическим местом, bottleneck, в машинном обучении. Все, что ваша модель будет знать о данных, решается на этом этапе. Больше, чем вы ей дадите, она не узнает.
Если вы в данных дадите явную подсказку об ответе, то она будет использовать эту подсказку, а реальные закономерности может и не выучить. К примеру, можно дать ей в качестве признака id покупателя, который каждую неделю покупает одно и то же. Если таких ситуаций будет много, то она и выучит, что надо предсказывать все по id. Когда же к вам придет новый покупатель или у старого что-то поменяется в поведении, модель начнет вести себя неадекватно.
Точно такую же роль может сыграть информация о номере эксперимента, лаборатории, в которой его проводили, аспиранте, который его проводил и т.д.
Такая ситуация называется data leakage.
Таким образом, если вы дадите модели только нерелевантную информацию, то она ничего из нее не вытащит.
At the end of the day, some machine learning projects succeed and some fail. What makes the difference? Easily the most important factor is the features used. @ Prof. Pedro Domingos
The algorithms we used are very standard for Kagglers. …We spent most of our efforts in feature engineering. … We were also very careful to discard features likely to expose us to the risk of over-fitting our model. @Xavier Conort, топ-участник Kaggle
Пример на Titanic
Для иллюстрации будут использованы примеры из книги "Real-World Machine Learning" из открытого репозитория и датасет Titanic.
Данный датасет представляет собой список пассажиров судна. Данные в нем не предобработаны, и в сыром виде не могут быть использованы для обучения модели.
import pandas as pd
# Download the data and save it in a variable called data
dataset = pd.read_csv(
"https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/titanic.csv"
) # Load the data using pandas
dataset[:5] # Show the first 5 lines
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
Если мы попытаемся обучить модель на таких данных, то у нас ничего не выйдет.
from sklearn.ensemble import RandomForestClassifier
x = dataset.drop("Survived", axis=1) # drop target
y = dataset["Survived"] # target
rf = RandomForestClassifier(random_state=42)
try:
rf.fit(x, y)
except ValueError as e:
print(e)
could not convert string to float: 'Braund, Mr. Owen Harris'
Посмотрим на информацию о признаках:
dataset.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 891 entries, 0 to 890 Data columns (total 12 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 PassengerId 891 non-null int64 1 Survived 891 non-null int64 2 Pclass 891 non-null int64 3 Name 891 non-null object 4 Sex 891 non-null object 5 Age 714 non-null float64 6 SibSp 891 non-null int64 7 Parch 891 non-null int64 8 Ticket 891 non-null object 9 Fare 891 non-null float64 10 Cabin 204 non-null object 11 Embarked 889 non-null object dtypes: float64(2), int64(5), object(5) memory usage: 83.7+ KB
Традиционно признаки делятся на:
Вещественные признаки бывают:

В датасете Титаник таким параметром будет SibSp — количество братьев/сестер/супругов на борту.
print(dataset.SibSp[:5])
0 1 1 1 2 0 3 1 4 0 Name: SibSp, dtype: int64
Или Parch — количество родителей/детей на борту.
print(dataset["Parch"].unique())
[0 1 2 5 3 4 6]

Понятно, что разделение часто условное. Тот же возраст можно посчитать и дискретной переменной (пользователь всегда нам сообщает свои полные года), и непрерывной (возраст можно считать с любой точностью, но никто не будет) )
Также иногда вещественные признаки делят на относительные (считаются относительно чего-то, уже нормированные и т.д.) и интервальные.
dataset[["Age", "Fare"]].head()
| Age | Fare | |
|---|---|---|
| 0 | 22.0 | 7.2500 |
| 1 | 38.0 | 71.2833 |
| 2 | 26.0 | 7.9250 |
| 3 | 35.0 | 53.1000 |
| 4 | 35.0 | 8.0500 |
Попробуем обучить модель чисто на вещественных признаках. PassengerId удалим, т.к. этот признак может приводить к утечке в данных.
from sklearn.model_selection import train_test_split
x = dataset.drop(columns=["Survived", "PassengerId"]) # drop target and id
y = dataset["Survived"] # target
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.2, random_state=42
)
# drop categorical
x_train_working = x_train.drop(
columns=["Pclass", "Name", "Sex", "Ticket", "Cabin", "Embarked"]
)
x_test_working = x_test.drop(
columns=["Pclass", "Name", "Sex", "Ticket", "Cabin", "Embarked"]
)
rf = RandomForestClassifier(random_state=42)
try:
rf.fit(x_train_working, y_train)
except ValueError as e:
print(e)
x_train_working.head()
Input X contains NaN. RandomForestClassifier does not accept missing values encoded as NaN natively. For supervised learning, you might want to consider sklearn.ensemble.HistGradientBoostingClassifier and Regressor which accept missing values encoded as NaNs natively. Alternatively, it is possible to preprocess the data, for instance by using an imputer transformer in a pipeline or drop samples with missing values. See https://scikit-learn.org/stable/modules/impute.html You can find a list of all estimators that handle NaN values at the following page: https://scikit-learn.org/stable/modules/impute.html#estimators-that-handle-nan-values
| Age | SibSp | Parch | Fare | |
|---|---|---|---|---|
| 331 | 45.5 | 0 | 0 | 28.5000 |
| 733 | 23.0 | 0 | 0 | 13.0000 |
| 382 | 32.0 | 0 | 0 | 7.9250 |
| 704 | 26.0 | 1 | 0 | 7.8542 |
| 813 | 6.0 | 4 | 2 | 31.2750 |
Проблема, что Age указан только для 714 пассажиров из 891. Его мы пока тоже удалим.
from sklearn.metrics import accuracy_score
x_train_working = x_train_working.drop(columns=["Age"])
x_test_working = x_test_working.drop(columns=["Age"])
rf = RandomForestClassifier(random_state=42)
rf.fit(x_train_working, y_train)
y_pred = rf.predict(x_test_working)
print(accuracy_score(y_test, y_pred))
0.6759776536312849
Точность предсказания 67.6%. Для улучшения качества попробуем добавить другие признаки.
Значение — принадлежность к какой-то из категорий. Традиционно делятся на сильно отличающиеся по свойствам:

В датасете Титаник таким признаком будет класс. Мы можем сказать, что первый класс лучше третьего, но не можем сказать, что сумма первого и второго даст третий.
print(dataset["Pclass"].unique())
[3 1 2]

В датасете Титаник таким признаком является Embarked (порт посадки).
print(dataset["Embarked"].unique())
# C = Cherbourg; Q = Queenstown; S = Southampton
['S' 'C' 'Q' nan]
Часто мы сталкиваемся с бинарными категориальными признаками, для которых известно только две возможных категории (например, биологический пол человека).
print(dataset["Sex"].unique())
['male' 'female']
Результат работы модели будет зависеть от ее признакового описания. Преобразование и генерация признаков — отдельный “вид искусства”, включающий:
Для того, чтобы понять, что новое признаковое описание лучше, нужно обучить модель.
Процесс подготовки признаков будет также зависеть от модели, которую мы используем. Например, one-hot encoding плохо работает со случайным лесом (подробности ниже).
В Label encoding каждой категории признака однозначно сопоставляется число. Данный подход хорошо работает для упорядоченных (ординальных) признаков.
Если признак неупорядоченный (номинальный), то могут возникнуть проблемы. Например, если мы обозначим: $$Уж = 1$$ $$Ёж = 2$$ $$Белка = 3$$ Получится, что $$Уж+Ёж = Белка$$ что не является свойством данных. Кроме того, мы не можем сказать, что уж “больше” ежа и сравнить его с белкой, но обучаемая модель про это не знает и будет пытаться их сравнить. Это может привести к низкому качеству модели и выучиванию неправильной информации. Например, дерево решений для выделения одной категории должно будет проделать несколько сравнений, что может не произойти в силу жадности алгоритма.
Некоторые модели (например, LightGBM) могут автоматически подбирать кодировку для категориальных признаков, если предоставить им информацию, что признак категориальный, для других моделей это нужно делать вручную.
У нас есть упорядоченный категориальный признак — класс, которым ехал пассажир. Добавим его к данным.
x_train_working["Pclass"] = x_train["Pclass"]
x_test_working["Pclass"] = x_test["Pclass"]
x_train_working[:5]
| SibSp | Parch | Fare | Pclass | |
|---|---|---|---|---|
| 331 | 0 | 0 | 28.5000 | 1 |
| 733 | 0 | 0 | 13.0000 | 2 |
| 382 | 0 | 0 | 7.9250 | 3 |
| 704 | 1 | 0 | 7.8542 | 3 |
| 813 | 4 | 2 | 31.2750 | 3 |
На практике часто используется one-hot encoding. Вместо одного категориального признака $X$ создается набор бинарных категориальных признаков, которые отвечают на вопрос $X == C$, где $C$ перебирает все возможные значения категориального признака.
Теперь, чтобы выбрать конкретное значение категориального признака, дереву решений достаточно задать один вопрос.
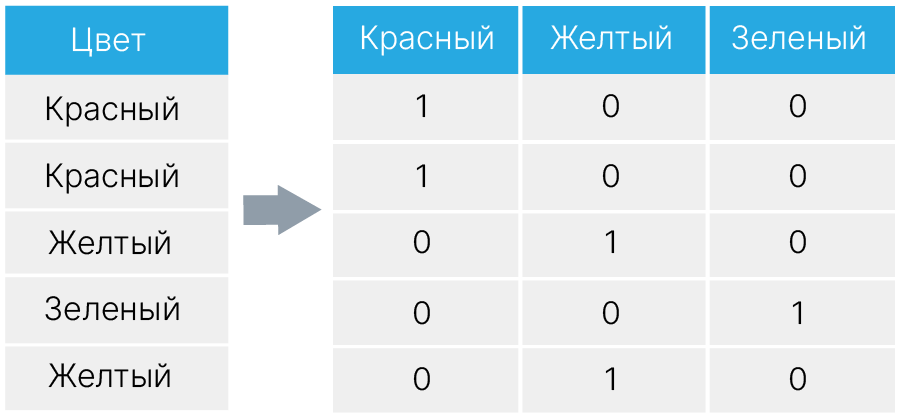
У такой схемы есть ряд недостатков:

Поэтому одну из категорий могут исключить при кодировании. Например, в примере выше можно исключить Рыбу, ведь если все три других признака-категории равны 0, то точно верно, что категория — Рыба.
У нас есть два признака с ограниченным количеством значений: Sex и Embarked.
Пол закодируем male = 1 female = 0.
sex = {"male": 1, "female": 0}
x_train_working["Sex"] = x_train["Sex"].map(sex)
x_test_working["Sex"] = x_test["Sex"].map(sex)
x_train_working[:5]
| SibSp | Parch | Fare | Pclass | Sex | |
|---|---|---|---|---|---|
| 331 | 0 | 0 | 28.5000 | 1 | 1 |
| 733 | 0 | 0 | 13.0000 | 2 | 1 |
| 382 | 0 | 0 | 7.9250 | 3 | 1 |
| 704 | 1 | 0 | 7.8542 | 3 | 1 |
| 813 | 4 | 2 | 31.2750 | 3 | 0 |
Еще один способ, который показал свою эффективность — это кодирование категориальной переменной по количеству встречаемости в данных.
| category | new_feature |
|---|---|
| food | 3 |
| equipment | 2 |
| food | 3 |
| food | 3 |
| equipment | 2 |
| clothes | 1 |
Его просто и быстро реализовать. Здесь также присутствует логика порядка, который возникает естественным образом. Чем больше число, тем чаще встречается категория. Также здесь отсутствует ложная линейная зависимость, в нашем случае equipment + clothes = food и для нас это действительно так, потому что наше кодирование отражает связь между категориями через их частоту.
Дополнительно стоит добавить шум к данным, чтобы избежать ситуации, когда разные категории кодируются одинаковым числом.
| category | new_feature |
|---|---|
| food | 2.3 |
| equipment | 2.04 |
| food | 2.3 |
| clothes | 2.6 |
| equipment | 2.04 |
| clothes | 2.6 |
Можем кодировать категориальный признак по какой-то статистике вещественного. Например, при прогнозировании покупок в интернет магазине может оказаться разумным кодировать категории товаров их средней ценой.
| category | product | price | new_feature |
|---|---|---|---|
| food | pizza | 30 | 17 |
| equipment | hammer | 140 | 170 |
| food | cucumber | 4 | 17 |
| clothes | boots | 100 | 60 |
| equipment | helmet | 200 | 170 |
| clothes | gloves | 20 | 60 |
В Target encoding каждая категория кодируется численным параметром, характеризующим то, что мы предсказываем. Например, можно каждую категорию категориального признака заменять на среднее целевого значения (mean target).
При этом может возникнуть проблема переобучения: для редких классов модель может научиться копировать значение mean target категориального признака в ответ, игнорируя другие признаки. Как с этим борются можно посмотреть здесь.
Так как у нас в качестве модели используется случайный лес, для Embarked будем использовать Label encoding. Мы не будем считать среднее. Используем Target, чтобы упорядочить метки. Посмотрим, какой процент выживших для каждого порта. Смотреть будем только на train выборке. Подглядывать в test — не честно!!!
import seaborn as sns
from matplotlib import pyplot as plt
plt.figure(figsize=(8, 4))
train_df = x_train.copy()
train_df["Survived"] = y_train
sns.barplot(x="Embarked", y="Survived", data=train_df)
plt.show()
Получили количество выживших $S<Q<C$. Упорядочим метки соответственно.
import numpy as np
emb = {np.nan: 0, "S": 0, "Q": 1, "C": 2}
x_train_working["Embarked"] = x_train["Embarked"].map(emb)
x_test_working["Embarked"] = x_test["Embarked"].map(emb)
x_train_working[5:10]
| SibSp | Parch | Fare | Pclass | Sex | Embarked | |
|---|---|---|---|---|---|---|
| 118 | 0 | 1 | 247.5208 | 1 | 1 | 2 |
| 536 | 0 | 0 | 26.5500 | 1 | 1 | 0 |
| 361 | 1 | 0 | 27.7208 | 2 | 1 | 2 |
| 29 | 0 | 0 | 7.8958 | 3 | 1 | 0 |
| 55 | 0 | 0 | 35.5000 | 1 | 1 | 0 |
У нас осталось еще 4 признака, с которыми непонятно, что делать: Name, Ticket, Cabin, Age.
Можно научить вашу модель саму сопоставлять каждой категории некий вектор определенной размерности. Для этого вначале сопоставляем каждой категории случайный вектор заданной длины. А далее изменяем этот вектор как обычные веса. Подробнее о формирование векторов-признаков (embedding) будет рассказано в других лекциях курса.

Рассмотрим поле Name. Это поле может нести информацию о поле, социальном статусе, происхождении, национальности, возрасте и т.д. Можно построить модели, которые будут это оценивать и отражать. Мы будем работать с числовыми представлениями текста в нашем курсе. Но пока мы можем использовать метод "пристального вглядывания" в данные.
x_train.Name[:5]
331 Partner, Mr. Austen 733 Berriman, Mr. William John 382 Tikkanen, Mr. Juho 704 Hansen, Mr. Henrik Juul 813 Andersson, Miss. Ebba Iris Alfrida Name: Name, dtype: object
В именах есть информация о социальном статусе:
и т.д.
Первые 4 встречаются чаще.
Извлечем все возможные титулы, они начинаются с пробела и заканчиваются точкой.
titles = dataset.Name.str.extract(" ([A-Za-z]+)\.", expand=False).unique()
print(titles)
['Mr' 'Mrs' 'Miss' 'Master' 'Don' 'Rev' 'Dr' 'Mme' 'Ms' 'Major' 'Lady' 'Sir' 'Mlle' 'Col' 'Capt' 'Countess' 'Jonkheer']
Сгруппируем некоторые с похожими значениями. Редкие запишем в нулевой класс.
titles = {
None: 0,
"Sir": 0,
"Countess": 0,
"Don": 0,
"Jonkheer": 0,
"Lady": 0,
"Capt": 0,
"Ms": 0,
"Mme": 0,
"Mlle": 0,
"Col": 0,
"Major": 0,
"Rev": 0,
"Dr": 0,
"Master": 1,
"Mrs": 2,
"Miss": 3,
"Mr": 4,
}
x_train_working["Title"] = x_train.Name.str.extract(" ([A-Za-z]+)\.", expand=False).map(
titles
)
x_test_working["Title"] = x_test.Name.str.extract(" ([A-Za-z]+)\.", expand=False).map(
titles
)
x_train_working[:5]
| SibSp | Parch | Fare | Pclass | Sex | Embarked | Title | |
|---|---|---|---|---|---|---|---|
| 331 | 0 | 0 | 28.5000 | 1 | 1 | 0 | 4 |
| 733 | 0 | 0 | 13.0000 | 2 | 1 | 0 | 4 |
| 382 | 0 | 0 | 7.9250 | 3 | 1 | 0 | 4 |
| 704 | 1 | 0 | 7.8542 | 3 | 1 | 0 | 4 |
| 813 | 4 | 2 | 31.2750 | 3 | 0 | 0 | 3 |
При работе с датой и временем мы можем представить дату и время в виде числа. Один из способов такого представления Unix Timestamp (количество секунд, прошедших с 1 января 1970-го года). Для ряда задач важна цикличность времени. Например, загруженность линии метро будет зависеть от времени дня (цикл 24 часа), дня недели (цикл 7 дней) и нерабочих праздничных дней (цикл год). Для прогнозирования количества электроэнергии, выработанной солнечной батареей, важно будет время дня (цикл 24 часа) и время года (цикл год).
В случае с такими признаками, как день недели или время суток, мы сталкиваемся с проблемой того, что нам нужно предложить кодирование, которое будет учитывать, что понедельник близок к воскресенью так же, как и ко вторнику, и т.д.
В случае деревьев решений и методов, на них основанных, можно "забить": такие методы сами разберутся. Для некоторых других методов, тех же нейросетей, правильно кодирование может улучшить качество и сходимость.
Давайте нанесем наши категории, например, дни недели, на окружность. Как это сделать? Пусть понедельнику соответствует 1, а воскресенью — 7. Далее посчитаем два таких вспомогательных признака по следующим формулам
weekdays = np.arange(1, 8) # create an array of weekdays
print(weekdays)
sina = np.sin(weekdays * np.pi * 2 / np.max(weekdays)) # feature 1
cosa = np.cos(weekdays * np.pi * 2 / np.max(weekdays)) # feature 2
[1 2 3 4 5 6 7]
plt.figure(figsize=(6, 6)) # Decide figure size
plt.scatter(sina, cosa) # Plot scatter of feature 1 vs feature 2
for i, z in enumerate(
("Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun")
): # for each day in a week
plt.text(sina[i], cosa[i], s=z) # add text labels to plot
Что делать дальше? По сути, мы уже все сделали. Теперь расстояния между понедельником и вторником и воскресеньем и понедельником одинаковые:
dist_mon_tue = (sina[1] - sina[0]) ** 2 + (
cosa[1] - cosa[0]
) ** 2 # distance between Monday and Tuesday
dist_sun_mon = (sina[6] - sina[0]) ** 2 + (
cosa[6] - cosa[0]
) ** 2 # distance between Sunday and Monday
print("Distance between Mon-Tue = %.2f" % dist_mon_tue)
print("Distance between Sun-Mon = %.2f" % dist_sun_mon)
Distance between Mon-Tue = 0.75 Distance between Sun-Mon = 0.75
То же самое верно и для любых отстоящих друг от друга на одинаковое число дней
dist_mon_wed = (sina[2] - sina[0]) ** 2 + (
cosa[2] - cosa[0]
) ** 2 # distance between Monday and Wednesday
dist_fri_sun = (sina[4] - sina[6]) ** 2 + (
cosa[4] - cosa[6]
) ** 2 # distance between Friday and Sunday
print("Distance between Mon-Wed = %.2f" % dist_mon_wed)
print("Distance between Fri-Sun = %.2f" % dist_fri_sun)
Distance between Mon-Wed = 2.45 Distance between Fri-Sun = 2.45
Таким образом, циклические признаки можно кодировать парой признаков (sin и cos), полученных по схеме, описанной выше.
Проблемы подхода:
Деревья решений могут решить задачу и так. А такое кодирование им, наоборот, будет мешать, т.к. они работают с одним признаком за раз.
Надо понимать, что важность исходной категориальной фичи неочевидным образом делится между двумя полученными из нее таким образом фичами.
В некоторых задачах one-hot работает лучше.
Для ряда задач может быть неважно конкретное значение признака. Важнее может оказаться факт превышения порога или наличия значения.
Например, уровень сахара крови выше $11.1$ ммоль/л может говорить о наличии у пациента сахарного диабета, что повлияет на результат лечения. А наличие высшего образования больше влияет на платежеспособность, чем средний балл диплома.
Для таких признаков можно попробовать использовать бинаризацию: превращение вещественного признака в бинарный по принципу “есть ли значение” или “больше ли значение определенного порога”.
Отойдем в сторону от Титаника и бинаризируем уровень сахара в крови.
from sklearn.preprocessing import Binarizer
# fmt: off
x = np.array([[1, 12],
[2, 7.6],
[3, 8.4],
[4, 13.5],
[5, 6.3]])
# fmt: on
transformer = Binarizer(threshold=11.1)
binarized = transformer.transform(np.expand_dims(x[:, 1], axis=1))
x_binarized = np.concatenate((x, binarized), axis=1)
print(x_binarized)
[[ 1. 12. 1. ] [ 2. 7.6 0. ] [ 3. 8.4 0. ] [ 4. 13.5 1. ] [ 5. 6.3 0. ]]
Часто данные доходят до нас с очень высокой точностью после запятой. Нужно ли это нашей модели? Часто нет. Иногда по факту два наблюдения не различаются по этому признаку (разница в пределах статошибки), но по признаку их отличить можно. Это может приводить к переобучению. В таких случаях разумно признаки округлить. Для этого полезно знать погрешность метода получения данных.
Например, есть признак со значением $\hat{x}=21.497263$ и погрешностью измерения $\Delta{x}=0.6294302$. Имеет смысл округлить значение признака до $x = 21.5$ с погрешностью $\pm 0.6$. Подробнее про расчет погрешности и округление можно почитать по ссылкам.
# fmt: off
x = np.array([[1, 12.121143145],
[2, 7.69458475974059],
[3, 8.434243214],
[4, 13.5958347545],
[5, 6.3323294098]])
# fmt: on
round_func = np.around(np.expand_dims(x[:, 1], axis=1), decimals=1)
x_round = np.concatenate((np.expand_dims(x[:, 0], axis=1), round_func), axis=1)
print(x_round)
[[ 1. 12.1] [ 2. 7.7] [ 3. 8.4] [ 4. 13.6] [ 5. 6.3]]
Нам могут быть не интересны точные значения (например, что видео набрало 1000 лайков, а не 1001).
К тому же, число просмотров/лайков некоторых видео может быть очень большим в сравнении с остальными, что будет приводить к неадекватному поведению. В итоге часть значений у нас встречается часто, а часть — очень редко, что негативно скажется на результате работы модели.
Бинирование — это метод группировки вещественных признаков в несколько категорий, определяемых диапазонами значений. При этом категория может кодироваться средним или медианным значением признака в диапазоне данной категории.
Просто бьем наши значения по диапазонам фиксированной длины. Так часто поступают с возрастом.
Гистограмма возраста разработчика

Длина диапазона не всегда обязана быть кратна определенному значению, например 10 годам. В социальных исследованиях может быть полезным разделение на возрастные группы, которые определяются занятостью: школьники, студенты, выпускники, пенсионеры и т.д. Бинирование на основе личного понимания данных называют Binning by Instinct.
Binning с фиксированной длиной бина или с использованием личного понимания данных не всегда работает хорошо. Полезно визуализировать результат разбиения. Например, рассмотрим распределение дохода разработчиков. Оно сильно скошено вправо.
Гистограмма дохода разработчика

Бинирование с фиксированной длиной бина не поможет справиться с редкими значениями.
В этой ситуации помогает бинирование, например, по квантилям — когда границы бина расставляются таким образом, чтобы между ними помещалась $1/4$ выборки.
Гистограмма дохода разработчика с квантилями

С ситуацией, когда распределение скошено вправо, работает и другой подход: прологаримфировать величину.
Гистограмма дохода разработчика после логарифмирования

Обобщением этого подхода является Box-Cox Transform, общей целью которой является придать данным вид, более похожий на нормальное распределение, с которым работает бoльшее число моделей и сходимость которого лучше.
В датасете Titanic отстался важный признак Age. Посмотрим, как он связан с выживаемостью.
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5))
train_df = x_train.copy()
train_df["Survived"] = y_train
women = train_df[train_df["Sex"] == "female"]
men = train_df[train_df["Sex"] == "male"]
ax = sns.histplot(
women[women["Survived"] == 1].Age.dropna(),
bins=18,
label="survived",
ax=axes[0],
kde=False,
color="#27a9e1",
linewidth=0,
)
ax = sns.histplot(
women[women["Survived"] == 0].Age.dropna(),
bins=40,
label="not survived",
ax=axes[0],
kde=False,
color="#ffab40",
linewidth=0,
)
ax.legend()
ax.set_title("Female")
ax = sns.histplot(
men[men["Survived"] == 1].Age.dropna(),
bins=18,
label="survived",
ax=axes[1],
kde=False,
color="#27a9e1",
linewidth=0,
)
ax = sns.histplot(
men[men["Survived"] == 0].Age.dropna(),
bins=40,
label="not survived",
ax=axes[1],
kde=False,
color="#ffab40",
linewidth=0,
)
ax.legend()
ax.set_title("Male")
plt.show()
Тут можно экспериментировать с бинированием, но мы поступим проще. Вспомним, что в поле Title зашита общая информация о возрасте, посчитаем матожидание и дисперсию возраста для Title и сгенерируем недостающие значения.
np.random.seed(42)
train_df = x_train.copy()
train_df["Title"] = x_train_working["Title"]
mean = {}
std = {}
for title in range(5):
data = train_df.loc[train_df["Title"] == title]
mean[title] = data["Age"].mean()
std[title] = data["Age"].std()
def add_age_val(data, mean, std):
for i, row in data.iterrows():
if np.isnan(row["Age"]):
title = int(row["Title"])
data.loc[i, "Age"] = round(
np.random.uniform(
low=int(mean[title] - std[title]),
high=int(mean[title] + std[title]),
),
1,
)
return data
x_train_working["Age"] = x_train["Age"]
x_test_working["Age"] = x_test["Age"]
x_train_working = add_age_val(x_train_working, mean, std)
x_test_working = add_age_val(x_test_working, mean, std)
x_train_working[:5]
| SibSp | Parch | Fare | Pclass | Sex | Embarked | Title | Age | |
|---|---|---|---|---|---|---|---|---|
| 331 | 0 | 0 | 28.5000 | 1 | 1 | 0 | 4 | 45.5 |
| 733 | 0 | 0 | 13.0000 | 2 | 1 | 0 | 4 | 23.0 |
| 382 | 0 | 0 | 7.9250 | 3 | 1 | 0 | 4 | 32.0 |
| 704 | 1 | 0 | 7.8542 | 3 | 1 | 0 | 4 | 26.0 |
| 813 | 4 | 2 | 31.2750 | 3 | 0 | 0 | 3 | 6.0 |
Посмотрим, что получилось на обработанных данных.
rf = RandomForestClassifier(random_state=42)
rf.fit(x_train_working, y_train)
y_pred = rf.predict(x_test_working)
print(accuracy_score(y_test, y_pred))
0.8212290502793296
Признаки могут по-разному взаимодейстовать, и некоторые модели в принципе не могут моделировать это взаимодействие.
Посмотрим это на игрушечном примере. Сгенерируем данные и попробуем решить задачу классификации с помощью линейной модели.
from sklearn.datasets import make_circles
np.random.seed(42)
x, y = make_circles(n_samples=400, factor=0.3, noise=0.05, random_state=42)
plt.figure(figsize=(5, 5))
violet = y == 0
yellow = y == 1
plt.scatter(x[violet, 0], x[violet, 1], c="blueviolet", s=20, edgecolor="k")
plt.scatter(x[yellow, 0], x[yellow, 1], c="yellow", s=20, edgecolor="k")
plt.xlabel("$x_1$", fontsize=20)
plt.ylabel("$x_2$", fontsize=20)
plt.show()
Видно, что тут нельзя провести плоскость, которая хорошо разделит наши классы.
Обучим модель и оценим точность.
from sklearn.linear_model import LogisticRegression
# We make a 80/20% train/test split of the data
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.2, random_state=42
)
model = LogisticRegression(max_iter=1000)
model.fit(x_train, y_train)
# Make predictions
print("Accuracy of the model = %.2f" % model.score(x_test, y_test))
Accuracy of the model = 0.65
Понимание взаимодействия признаков может упростить решаемую задачу. Например, введение нового признака $z= x_1^2+x_2^2$ для наших данных позволит линейной модели решить задачу классификации. Добавим этот признак:
df = pd.DataFrame(x, columns=["x_1", "x_2"])
df["z"] = x[:, 0] ** 2 + x[:, 1] ** 2
df
| x_1 | x_2 | z | |
|---|---|---|---|
| 0 | 0.261024 | 0.122538 | 0.083149 |
| 1 | -0.245087 | 0.202270 | 0.100981 |
| 2 | 0.489471 | 0.882643 | 1.018641 |
| 3 | 0.368505 | 0.055743 | 0.138904 |
| 4 | -0.981276 | 0.193832 | 1.000475 |
| ... | ... | ... | ... |
| 395 | -0.617948 | 0.865083 | 1.130229 |
| 396 | -0.898005 | -0.210396 | 0.850679 |
| 397 | -0.089725 | 0.296459 | 0.095939 |
| 398 | 0.099591 | -0.320610 | 0.112709 |
| 399 | -1.015698 | -0.164124 | 1.058579 |
400 rows × 3 columns
Обучим модель с новым признаком:
# We make a 80/20% train/test split of the data
x_train, x_test, y_train, y_test = train_test_split(
df.values, y, test_size=0.2, random_state=42
)
model = LogisticRegression(max_iter=1000)
model.fit(x_train, y_train)
# Make predictions
print("Accuracy of the model = %.2f" % model.score(x_test, y_test))
Accuracy of the model = 1.00
Как мы видим, наша линейная модель теперь полностью решает задачу. Визуализируем данные с новым признаком:
def plot_data(x, y, total_len=400, s=50, threshold=21.5):
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
ax.scatter(xs=x[:, 0], ys=x[:, 1], zs=x[:, 2], c=y, s=s)
# plot the decision function
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
ax.plot_surface(XX, YY, XX * YY * 0.2, alpha=0.2)
ax.set(xlabel="$x_1$", ylabel="$x_2$", zlabel="$z$")
return ax
total_len = 400
ax = plot_data(df.values, y, total_len=total_len)
Могут быть и более высокоуровневые взаимодействия, когда взаимодействуют много разных признаков.
Взаимодействия могут быть самые разные — много способов кодировать. Например, добавлять в число признаков их произведение, возводить в степень, брать логарифм и множество других вариаций.
Если у вас есть модель, обученная на другом датасете, можно генерировать признаки при помощи нее. Например, при помощи случайного леса.

Генерация бинарного признакового пространства с помощью RandomForest
Хорошие источники:
Попробуем обработать данные по-другому.
dataset = pd.read_csv(
"https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/titanic.csv"
) # Load the data using pandas
dataset[:5] # Show the first 5 lines
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
Часть полей можно исключить (имя);
Часть можно преобразовать в числа (пол, порт посадки ...);
Непрерывные данные можно нормировать (здесь вместо этого берется квадратный корень из цены);
На основании некоторых можно создать новые, более полезные для модели (номер кабины).
cabin_data = array(["C65", "", "E36", "C54", "B57 B59 B63 B66"]) -> [['C', 65, 1], ['X', -1, 0], ['E', 36, 1], ['C', 54, 1], ['B', 57, 4]]
# The categorical-to-numerical function
# Changed to automatically add column names
def cat_to_num(data): # one-hot encoding
categories = set(data)
features = {}
for cat in categories:
binary = data == cat
if len(set(binary)) == 1:
# Ignore features where all values equal
continue
new_key = f"{data.name}={cat}"
features[new_key] = binary.astype("int")
return pd.DataFrame(features)
def cabin_features(data):
features = []
for cabin in data:
cabins = str(cabin).split(" ")
n_cabins = len(cabins)
# First char is the cabin_char
try:
cabin_char = cabins[0][0]
except IndexError:
cabin_char = "X"
n_cabins = 0
# The rest is the cabin number
try:
cabin_num = int(cabins[0][1:])
except:
cabin_num = -1
# Add 3 features for each passanger
features.append([cabin_char, cabin_num, n_cabins])
features = np.array(features)
dic_of_features = {
"Cabin_num": features[:, 1].astype("int"),
"N_cabins": features[:, 2].astype("int"),
}
out = pd.DataFrame(dic_of_features)
char_column = pd.DataFrame({"Cabin_char": features[:, 0]})
cabin_ch = cat_to_num(char_column["Cabin_char"])
return out.join(cabin_ch)
def prepare_data(data):
"""Takes a dataframe of raw data and returns ML model features"""
# Initially, we build a model only on the available numerical values
features = data.drop(
[
"PassengerId",
"Survived",
"Fare",
"Name",
"Sex",
"Ticket",
"Cabin",
"Embarked",
],
axis=1,
)
# Setting missing age values to -1
features["Age"] = data["Age"].fillna(-1)
# Adding the sqrt of the fare feature
features["sqrt_Fare"] = np.sqrt(data["Fare"])
# Adding gender categorical value
features = features.join(cat_to_num(data["Sex"]))
# Adding Embarked categorical value
features = features.join(cat_to_num(data["Embarked"]))
# Split cabin
features = features.join(cabin_features(data["Cabin"]))
return features
features = prepare_data(dataset) # Create variable features
features[:5] # Display first 5 rows
| Pclass | Age | SibSp | Parch | sqrt_Fare | Sex=male | Sex=female | Embarked=C | Embarked=S | Embarked=Q | ... | N_cabins | Cabin_char=T | Cabin_char=F | Cabin_char=G | Cabin_char=C | Cabin_char=E | Cabin_char=B | Cabin_char=A | Cabin_char=n | Cabin_char=D | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 22.0 | 1 | 0 | 2.692582 | 1 | 0 | 0 | 1 | 0 | ... | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 38.0 | 1 | 0 | 8.442944 | 0 | 1 | 1 | 0 | 0 | ... | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 3 | 26.0 | 0 | 0 | 2.815138 | 0 | 1 | 0 | 1 | 0 | ... | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 1 | 35.0 | 1 | 0 | 7.286975 | 0 | 1 | 0 | 1 | 0 | ... | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 3 | 35.0 | 0 | 0 | 2.837252 | 1 | 0 | 0 | 1 | 0 | ... | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
5 rows × 21 columns
Теперь модель можно обучать:
# We make a 80/20% train/test split of the data
features = prepare_data(dataset)
x_train, x_test, y_train, y_test = train_test_split(
features, dataset["Survived"], test_size=0.2, random_state=42
)
model = LogisticRegression(max_iter=1000)
model.fit(x_train, y_train)
# Make predictions
print("Accuracy of the model = %.2f" % model.score(x_test, y_test))
Accuracy of the model = 0.78
В первый раз мы обработали признаки лучше. Вероятно, это связанно с оценкой Age через Title.
Для целей предварительной обработки признаков существует множество инструментов, в том числе модуль preprocessing в пакете sklearn.
Аналогичные подмодули или целые библиотеки есть и для разных задач, связанных с нейронными сетями (torchvision, torchaudio и прочее)
from sklearn.compose import make_column_transformer
from sklearn.compose import make_column_selector
from sklearn.preprocessing import OneHotEncoder
# Make one shot encoded representation
one_hot_encoder = make_column_transformer(
(
OneHotEncoder(
sparse_output=False, # if False return array, if True return sparse matrix
handle_unknown="ignore",
), # ignore if an unknown categorical feature is present during transform
make_column_selector(dtype_include="category"),
), # selection of dtypes to include
remainder="passthrough",
) # all columns that were not specified in transformers will be passed through
# preprocessing features using sklearn.preprocessing
features = dataset.drop(
["PassengerId", "Survived", "Fare", "Name", "Sex", "Ticket", "Cabin", "Embarked"],
axis=1,
)
# make Cabin features, examples: None -> 'X', C85 -> 'C', B42 -> 'B'
features["Cabin"] = (
dataset["Cabin"].fillna("X").apply(lambda x: x[0]).astype("category")
)
def get_cab_num(cab):
try:
return int(cab.split()[0][1:]) # get cabin num (C85 -> 85)
except:
return -1 # if dont know num, return -1 (X -> -1)
features["Cabin_num"] = (
dataset["Cabin"].fillna("X").apply(lambda x: get_cab_num(x))
) # get cabin num
features["N_cabins"] = (
dataset["Cabin"].fillna("X").str.split(" ").apply(lambda x: len(x))
) # num of cabins (C23 C25 C27 -> 3)
features["Sex"] = dataset["Sex"].astype("category") # male/female
features["Embarked"] = (
dataset["Embarked"].fillna("X").astype("category")
) # Categories: ['C', 'Q', 'S', 'X']
features["sqrt_Fare"] = np.sqrt(dataset["Fare"]) # normalize by sqrt
features["Age"] = dataset["Age"].fillna(-1) # NaN -> -1
# 80/20% train/test split of the data
x_train, x_test, y_train, y_test = train_test_split(
features, dataset["Survived"], test_size=0.2, random_state=42
)
one_hot_encoder.fit(x_train) # fit one-hot encoder to x_train
x_train_ohe = one_hot_encoder.transform(
x_train
) # transform x_train with the one-hot encoder
x_test_ohe = one_hot_encoder.transform(
x_test
) # transform x_test with the one-hot encoder
model = LogisticRegression(max_iter=1000) # specify maximum iterations
model.fit(x_train_ohe, y_train) # fit model to the training data
# Make predictions
print(
"Accuracy of the model = %.2f" % model.score(x_test_ohe, y_test)
) # calculate the accuracy of the model
Accuracy of the model = 0.78
Рассмотрим пример, в котором для кодирования значений признаков используется результат работы ансамбля деревьев, а затем на закодированных данных обучается линейная модель.
В этом примере сначала на отдельной выборке обучается ансамбль деревьев (случайный лес и градиентный бустинг), и каждому листу каждого дерева в ансамбле присваивается уникальный индекс.
Для кодирования с помощью обученного ансамбля каждый объект проходит по всем деревьям. В каждом дереве он оказывается в одном из листьев и получает в качестве нового признака индекс этого листа. Таким образом создается новое пространство признаков. После этого новые признаки (индексы листьев) кодируются по принципу one-hot ecnoding.
Для начала создадим датасет и разобьем его на три отдельные части:
Важно обучать ансамбль деревьев на ином подмножестве обучающих данных, чем модель линейной регрессии, чтобы избежать переобучения, в частности, если общее количество листьев окажется равно количеству обучающих образцов или близко к нему.
### https://scikit-learn.org/stable/auto_examples/ensemble/plot_feature_transformation.html#sphx-glr-auto-examples-ensemble-plot-feature-transformation-py
from sklearn.datasets import make_classification
np.random.seed(42)
# define dummy dataset
x, y = make_classification(n_samples=80000, random_state=42)
# split dataset into subsets for training ensemble and linear model and final testing of the linear model
x_full_train, x_test, y_full_train, y_test = train_test_split(
x, y, test_size=0.5, random_state=42
)
# split training subset into parts for ensemble training and for linear model training
x_train_ensemble, x_train_linear, y_train_ensemble, y_train_linear = train_test_split(
x_full_train, y_full_train, test_size=0.5, random_state=42
)
Теперь можем обучить ансабли на специально отложенных для этого данных, а затем применить их для кодирования обучающей и тестовой выборок для линейной модели. На закодированных данных мы обучаем модель логистической регрессии, а затем строим ROC-кривые, чтобы сравнить качество разных подходов.
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.metrics import roc_curve
n_estimator = 10
# Supervised transformation based on random forests
rf = RandomForestClassifier(max_depth=3, n_estimators=n_estimator, random_state=42)
rf_enc = OneHotEncoder()
rf_lm = LogisticRegression(max_iter=1000)
rf.fit(x_train_ensemble, y_train_ensemble)
rf_enc.fit(rf.apply(x_train_ensemble)) # apply method return leaf indices
rf_lm.fit(rf_enc.transform(rf.apply(x_train_linear)), y_train_linear)
y_pred_rf_lm = rf_lm.predict_proba(rf_enc.transform(rf.apply(x_test)))[:, 1]
fpr_rf_lm, tpr_rf_lm, _ = roc_curve(y_test, y_pred_rf_lm)
# Supervised transformation based on gradient boosted trees
grd = GradientBoostingClassifier(n_estimators=n_estimator, random_state=42)
grd_enc = OneHotEncoder()
grd_lm = LogisticRegression(max_iter=1000)
grd.fit(x_train_ensemble, y_train_ensemble)
grd_enc.fit(grd.apply(x_train_ensemble)[:, :, 0]) # apply method return leaf indices
grd_lm.fit(grd_enc.transform(grd.apply(x_train_linear)[:, :, 0]), y_train_linear)
y_pred_grd_lm = grd_lm.predict_proba(grd_enc.transform(grd.apply(x_test)[:, :, 0]))[
:, 1
]
fpr_grd_lm, tpr_grd_lm, _ = roc_curve(y_test, y_pred_grd_lm)
Также для сравнения протестируем обученные ансамбли на той же тестовой выборке.
# The random forest model by itself
y_pred_rf = rf.predict_proba(x_test)[:, 1]
fpr_rf, tpr_rf, _ = roc_curve(y_test, y_pred_rf)
# The gradient boosted model by itself
y_pred_grd = grd.predict_proba(x_test)[:, 1]
fpr_grd, tpr_grd, _ = roc_curve(y_test, y_pred_grd)
Построим ROC-кривые для четырех моделей:
# Plot figure 1 and figure 2 with subplots
fig, [ax1, ax2] = plt.subplots(nrows=1, ncols=2, figsize=(16, 6))
ax1.plot([0, 1], [0, 1], "k--")
ax1.plot(fpr_rf, tpr_rf, label="RF")
ax1.plot(fpr_rf_lm, tpr_rf_lm, label="RF + LR")
ax1.plot(fpr_grd, tpr_grd, label="GBT")
ax1.plot(fpr_grd_lm, tpr_grd_lm, label="GBT + LR")
ax1.set_xlabel("False positive rate")
ax1.set_ylabel("True positive rate")
ax1.set_title("ROC curve")
ax1.legend(loc="best")
ax2.set_xlim(0, 0.2)
ax2.set_ylim(0.8, 1)
ax2.plot([0, 1], [0, 1], "k--")
ax2.plot(fpr_rf, tpr_rf, label="RF")
ax2.plot(fpr_rf_lm, tpr_rf_lm, label="RF + LR")
ax2.plot(fpr_grd, tpr_grd, label="GBT")
ax2.plot(fpr_grd_lm, tpr_grd_lm, label="GBT + LR")
ax2.set_xlabel("False positive rate")
ax2.set_ylabel("True positive rate")
ax2.set_title("ROC curve (zoomed in at top left)")
ax2.legend(loc="best")
plt.show()
На этом модельном примере видим, что применение комбинации моделей (кодирование данных с помощью ансамбля деревьев и классификация с помощью линейной модели) позволяет достичь более высокого качества классификации.
1. Закодированные данные, полученные по некоторой известной конвенции.
Иногда данные могут не содержать значимую информацию непосредственно, а лишь являться ссылкой на неё. Очевидными примерами таких данных можно назвать:
Так, в случае анализа содержащих IP адреса данных, представляется куда более целесообразным предварительно извлечь содержащуюся информацию явно:
xxx.xxx.xxx.xxx -> регион, провайдер.
Мы неявно требуем, отправляя данные такого типа в модель в сыром виде, чтобы модель научилась самостоятельно их расшифровывать и интерпретировать.
2. Данные, записанные в неинвариантной форме
Рассмотрим следующий, намеренно упрощенный пример:
Предположим, мы аккуратно нарисовали на двух разных листах бумаги пару геометрически равных треугольников. На каждом из листов взяли по одному из углов в качестве начала координат соответственно и выписали координаты вершин наших треугольников. Три пары чисел — координаты вершин — наши данные, которые однозначно характеризуют каждый из рассматриваемых треугольников. Будут ли численно совпадать эти данные для геометрически равных треугольников?
Очевидно, нет. Чтобы можно было сразу определить, равны ли треугольники, по описывающим их данным, вместо координат вершин нам следует описать их в виде набора некоторых инвариантных признаков. Для треугольника это может быть или информация о длинах трех сторон, или длины двух сторон и величина угла между ними, или же длина одной из сторон вместе с величинами прилежащих к ней углов.
Как можно заметить из рассмотренного выше примера, записанные в неинвариантной форме данные могут быть вырождены: один и тот же объект может быть описан множеством существенно различных значений признаков.
Примеры:
Так, при построении модели предсказания пространственной структуры белка по входящей в него аминокислотной последовательности (см. AlphaFold), конструктивный подход предполагает инвариантное описание молекулы в качестве матрицы попарных расстояний между атомами.
Передавая неинвариантные данные модели в сыром виде, приходится нереалистично рассчитывать на то, что модель сама сможет выделить из них значащие инвариантные свойства исследуемых объектов.
В прошлых лекциях вы познакомились с тем, что такое признаки. Сегодня мы попытаемся научиться отделять полезные признаки от бесполезных, а также понижать размерность пространства признаков.
Количество признаков в данных может оказаться избыточным:
В первом случае логично предложить замену группы зависимых признаков через объединение их в один новый композитный признак. Замена группы старых признаков новым может позволить сохранить всю значимую информацию, одновременно избавляясь от проблемы избыточного описания данных.
Во втором случае можно ожидать улучшение качества предсказания модели, если удастся отфильтровать действительно важные признаки. Включение в данные не важных признаков, очевидно, не может улучшить качество обученной на таких данных модели, но, как ни странно, может значительно ухудшить.
Некоторые признаки могут оказаться шумом
Предположим, мы добавили в набор данных для обучения некоторой модели регрессии несколько тысяч вещественных признаков, которые представляют собой случайные числа из стандартного нормального распределения — белый шум. Случайные числа, очевидно, никак не могут быть связаны с нашей целевой переменной. Тем не менее, в силу большого числа таких шумовых признаков, значения некоторых из них могут оказаться случайно скоррелированы со значениям нашей целевой переменной в рамках обучающей выборки. Обученная на таких данных модель будет стараться предсказывать целевую переменную, явно учитывая значения признаков, которые на самом деле не имеют никакого смысла. При попытке построения предсказания данной моделью на тестовой выборке мы неизбежно заметим значительное снижение качества предсказания. Полученная модель обладает плохой обобщающей способностью.
В более общем случае можно говорить, что в многомерном пространстве почти всегда можно найти корреляции. См. картинку.

Скорость работы модели часто имеет значение
Кроме того, в практически важных задачах часто приходится искать компромисс между точностью предсказания модели и необходимым для его получения временем. Спектр таких задач достаточно широк: от проблем построения быстрых систем ранжирования рекламных объявлений в интернет-маркетинге до построения быстрых систем распознавания сложных событий на ускорителях заряженных частиц. Вычислительная сложность модели, очевидно, растёт с увеличением числа входных признаков, поэтому работающие с меньшим числом признаков модели являются для таких задач предпочтительными.
Можно попытаться перебрать все возможные комбинации признаков. Но даже для 100 признаков такой подход будет считаться до конца Вселенной.
Потому прибегают к эвристикам, которые, очевидно, могут пропускать оптимальное решение
Самый простой подход к отбору признаков — это одномерный подход. В нём оценивается связь каждого признака с целевой переменной, например, измеряется корреляция. Такой подход довольно простой, он не учитывает сложные закономерности, в нём все признаки считаются независимыми, тогда как в машинном обучении модели учитывают взаимное влияние признаков, их пар или даже более сложные действия на целевую переменную.
Пусть у нас есть $N$ объектов с $K$ признаками, и для каждого объекта задана целевая переменная или ответ. Обозначим матрицу объектов-признаков через $X \in \mathbf{R}^{N \times M} $, а вектор ответов через $Y$. Для удобства введем следующие дополнительные обозначения:
Задача — оценить предсказательную силу (информативность) каждого признака, то есть насколько хорошо по данному признаку можно предсказывать целевую переменную. Данные оцененной информативности можно использовать, чтобы отобрать $K$ лучших признаков или признаки, у которых значение информативности больше порога (например, некоторой квантили распределения информативности).
Один из самых простых методов измерения связи между признаком и ответами — это корреляция. Корреля́ция (от лат. correlatio «соотношение»), или корреляцио́нная зави́симость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.
Коэффициент корреляции по признаку $j$ $\left(R_j\right)$ определяется формулой:
$$R_j = \frac{\sum_{i=1}^{N} \left(X_{ij} - \overline{X_j}\right)\left(Y_{i} - \overline{Y}\right)} {\sqrt{ \sum_{i=1}^{N}\left(X_{ij} - \overline{X_j}\right)^2\sum_{i=1}^{N} \left(Y_{i} - \overline{Y}\right)^2}}$$Чем больше по модулю корреляция между признаком и целевой переменной, тем более информативным является данный признак. При этом она максимальна по модулю $\left(R_j = \pm1\right)$, если между признаком и целевой переменной есть линейная связь, то есть если целевую переменную можно строго линейно выразить через значение признака. Это означает, что корреляция измеряет только линейную информативность, то есть способность признака линейно предсказывать целевую переменную. Вообще говоря, корреляция рассчитана на вещественные признаки и вещественные ответы. Тем не менее, её можно использовать в случае, если признаки и ответы бинарные (имеет смысл кодировать бинарный признак с помощью значений $\pm1$)
import pandas as pd
dataset = pd.read_csv(
"https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/titanic.csv"
) # Load the data using pandas
dataset.head(5) # Show the first 5 lines
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
import numpy as np
# The categorical-to-numerical function
# Changed to automatically add column names
def cat_to_num(data): # one-hot encoding
categories = set(data)
features = {}
for cat in categories:
binary = data == cat
if len(set(binary)) == 1:
# Ignore features where all values equal
continue
new_key = f"{data.name}={cat}"
features[new_key] = binary.astype("int")
return pd.DataFrame(features)
def cabin_features(data):
features = []
for cabin in data:
cabins = str(cabin).split(" ")
n_cabins = len(cabins)
# First char is the cabin_char
try:
cabin_char = cabins[0][0]
except IndexError:
cabin_char = "X"
n_cabins = 0
# The rest is the cabin number
try:
cabin_num = int(cabins[0][1:])
except:
cabin_num = -1
# Add 3 features for each passanger
features.append([cabin_char, cabin_num, n_cabins])
features = np.array(features)
dic_of_features = {
"Cabin_num": features[:, 1].astype("int"),
"N_cabins": features[:, 2].astype("int"),
}
out = pd.DataFrame(dic_of_features)
char_column = pd.DataFrame({"Cabin_char": features[:, 0]})
cabin_ch = cat_to_num(char_column["Cabin_char"])
return out.join(cabin_ch)
def prepare_data(data):
"""Takes a dataframe of raw data and returns ML model features"""
# Initially, we build a model only on the available numerical values
features = data.drop(
[
"PassengerId",
"Survived",
"Fare",
"Name",
"Sex",
"Ticket",
"Cabin",
"Embarked",
],
axis=1,
)
# Setting missing age values to -1
features["Age"] = data["Age"].fillna(-1)
# Adding the sqrt of the fare feature
features["sqrt_Fare"] = np.sqrt(data["Fare"])
# Adding gender categorical value
features = features.join(cat_to_num(data["Sex"]))
# Adding Embarked categorical value
features = features.join(cat_to_num(data["Embarked"]))
# Split cabin
features = features.join(cabin_features(data["Cabin"]))
return features
features = prepare_data(dataset) # Create variable features
features.head(5) # Display first 5 rows
| Pclass | Age | SibSp | Parch | sqrt_Fare | Sex=male | Sex=female | Embarked=C | Embarked=S | Embarked=Q | ... | N_cabins | Cabin_char=T | Cabin_char=F | Cabin_char=G | Cabin_char=C | Cabin_char=E | Cabin_char=B | Cabin_char=A | Cabin_char=n | Cabin_char=D | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 22.0 | 1 | 0 | 2.692582 | 1 | 0 | 0 | 1 | 0 | ... | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 38.0 | 1 | 0 | 8.442944 | 0 | 1 | 1 | 0 | 0 | ... | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 3 | 26.0 | 0 | 0 | 2.815138 | 0 | 1 | 0 | 1 | 0 | ... | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 1 | 35.0 | 1 | 0 | 7.286975 | 0 | 1 | 0 | 1 | 0 | ... | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 3 | 35.0 | 0 | 0 | 2.837252 | 1 | 0 | 0 | 1 | 0 | ... | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
5 rows × 21 columns
from scipy import stats
from sklearn.model_selection import train_test_split
features = prepare_data(dataset) # produce feature
x_train, x_test, y_train, y_test = train_test_split(
features, dataset["Survived"], test_size=0.2, random_state=42
)
correlations = [] # create a storage for correlations
for column in features:
r, p_value = stats.pearsonr(x_train[column], y_train) # compute Pearson and R
correlations.append((column, abs(r))) # add to storage
df = pd.DataFrame(correlations, columns=["Column", "Correlation"]).sort_values(
"Correlation", ascending=False
)
df.head(df.shape[0])
| Column | Correlation | |
|---|---|---|
| 5 | Sex=male | 0.541750 |
| 6 | Sex=female | 0.541750 |
| 0 | Pclass | 0.321750 |
| 19 | Cabin_char=n | 0.300371 |
| 4 | sqrt_Fare | 0.295597 |
| 10 | Cabin_num | 0.237024 |
| 17 | Cabin_char=B | 0.176650 |
| 7 | Embarked=C | 0.159632 |
| 16 | Cabin_char=E | 0.144024 |
| 8 | Embarked=S | 0.142371 |
| 15 | Cabin_char=C | 0.127315 |
| 20 | Cabin_char=D | 0.123186 |
| 3 | Parch | 0.078311 |
| 13 | Cabin_char=F | 0.055922 |
| 11 | N_cabins | 0.051495 |
| 2 | SibSp | 0.047602 |
| 1 | Age | 0.043465 |
| 12 | Cabin_char=T | 0.029137 |
| 9 | Embarked=Q | 0.006097 |
| 18 | Cabin_char=A | 0.005813 |
| 14 | Cabin_char=G | 0.005783 |
Следующая идея такая: давайте посчитаем ROC-AUC по признаку, учитывая его как предсказание модели. Если ROC-AUC высокий (нас интересуют только абсолютные значения), то признак важный.
from sklearn.metrics import roc_auc_score
features = prepare_data(dataset)
x_train, x_test, y_train, y_test = train_test_split(
features, dataset["Survived"], test_size=0.2, random_state=42
)
rocs = [] # create a storage for ROCs
for column in features:
# use feature as score directly
r1 = roc_auc_score(y_score=x_train[column], y_true=y_train)
# use feature as score in reversed manner
r2 = roc_auc_score(y_score=-x_train[column], y_true=y_train)
r = max(r1, r2)
rocs.append((column, r))
df = pd.DataFrame(rocs, columns=["Column", "Rocs"]).sort_values(
"Rocs", ascending=False
) # sort from highest to lowest
df.head(df.shape[0])
| Column | Rocs | |
|---|---|---|
| 6 | Sex=female | 0.765614 |
| 5 | Sex=male | 0.765614 |
| 4 | sqrt_Fare | 0.677138 |
| 0 | Pclass | 0.673802 |
| 10 | Cabin_num | 0.629328 |
| 19 | Cabin_char=n | 0.629101 |
| 8 | Embarked=S | 0.564660 |
| 7 | Embarked=C | 0.562676 |
| 3 | Parch | 0.558794 |
| 17 | Cabin_char=B | 0.540978 |
| 1 | Age | 0.535687 |
| 15 | Cabin_char=C | 0.534187 |
| 2 | SibSp | 0.533822 |
| 16 | Cabin_char=E | 0.526825 |
| 20 | Cabin_char=D | 0.520489 |
| 11 | N_cabins | 0.507450 |
| 13 | Cabin_char=F | 0.507429 |
| 9 | Embarked=Q | 0.501748 |
| 12 | Cabin_char=T | 0.501126 |
| 18 | Cabin_char=A | 0.500706 |
| 14 | Cabin_char=G | 0.500387 |

У подхода, при котором важности всех признаков оцениваются по отдельности, есть свои недостатки. На левом рисунке изображена двумерная выборка, для которой необходимо решить задачу классификации. Если спроецировать данную выборку на ось абсцисс, то она будет разделима, хотя и будут присутствовать ошибки. Если же спроецировать данную выборку на ось ординат, то все объекты разных классов перемешаются, и выборка будет неразделима. В этом случае при использовании любого метода одномерного оценивания информативности первый признак будет информативен, а второй — совершенно неинформативен.
Тем не менее, видно, что если использовать эти признаки одновременно, то классы будут разделимы идеально. На самом деле, второй признак важен, но он важен только в совокупности с первым, и методы одномерного оценивания информативности не способны это определить. На рисунке справа показана выборка, на которой одномерные методы оценки информативности работают ещё хуже. В этом случае, если спроецировать выборку на ось абсцисс или ординат, то объекты классов перемешаются, и в обоих случаях данные будут совершенно неразделимы. И, согласно любому из описанных методов, оба признака неинформативны. Тем не менее, если использовать их одновременно, то, например, решающее дерево может идеально решить данную задачу классификации.
Пример: влияние роста и веса при предсказании вероятности сердечного заболевания. Избыточный вес может являться важным фактором, но оценить, является ли он избыточным или нормальным, можно только зная рост пациента.
Жадные методы отбора признаков по сути являются надстройками над методами обучения моделей. Они перебирают различные подмножества признаков и выбирают то из них, которое дает наилучшее качество определённой модели машинного обучения. Данный процесс устроен следующим образом. Обучение модели считается черным ящиком, который на вход принимает информацию о том, какие из его признаков можно использовать при обучении модели, обучает модель, и дальше каким-то методом оценивается качество такой модели, например, по отложенной выборке или кросс-валидации. Таким образом, задача, которую необходимо решить — это оптимизация функционала качества модели по подмножеству признаков.
Полный перебор
$S=\{S_1, \dots ,S_n\}$ — множество всех признаков
$\varnothing \;\{S_1\}...\{S_n\}; \{S_1S_2\}, \{S_1S_3\}, \dots , \{S_1S_n\}$
$\{S_2,S_3\}; \{\dots\}; \{S_1 \dots S_n\}$

Самый простой способ решения данной задачи — это полный перебор всех подмножеств признаков и оценивание качества на каждом подмножестве. Итоговое подмножество — то, на котором качество модели наилучшее. Этот перебор можно структурировать и перебирать подмножества последовательно: сначала те, которые имеют мощность 1 (наборы из 1 признака), потом наборы мощности 2, и так далее. Это подход очень хороший, он найдет оптимальное подмножество признаков, но при этом очень сложный, поскольку всего таких подмножеств $2^d$, где $d$ — число признаков. Если признаков много — сотни или тысячи, то такой перебор невозможен: он займет слишком много времени, возможно, сотни лет или больше. Поэтому, такой метод подходит либо при небольшом количестве признаков, либо если известно, что информативных признаков очень мало, единицы.
Жадное добавление

Если же признаков много и известно, что многие из них информативны, то нужно применять жадную стратегию. Жадная стратегия используется всегда, когда полный перебор не подходит для решения задачи. Например, может оказаться неплохой стратегия жадного наращивания (жадного добавления). Сначала находится один признак, который дает наилучшее качество модели (наименьшую ошибку $Q$):
$i_1 = argmin Q(i)$.
Тогда множество, состоящее из этого признака:
$J_1 = {i_1}$
Дальше к этому множеству добавляется еще один признак так, чтобы как можно сильнее уменьшить ошибку модели:
$i_2 =argminQ(i_1,i)$, $J_2 ={i_1,i_2}$.
Далее каждый раз добавляется по одному признаку, образуются множества $J_3 , J_4 , . . . .$ Если в какой-то момент невозможно добавить новый признак так, чтобы уменьшить ошибку, процедура останавливается. Жадность процедуры заключается в том, что как только какой-то признак попадает в оптимальное множество, его нельзя оттуда удалить.
import joblib
import sys
sys.modules["sklearn.externals.joblib"] = joblib
from mlxtend.feature_selection import SequentialFeatureSelector
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold
sfs = SequentialFeatureSelector(
LogisticRegression(max_iter=1000),
k_features=8, # number of features to select
forward=True,
floating=False,
scoring="accuracy",
cv=KFold(n_splits=5, shuffle=True, random_state=42),
)
sfs.fit(x_train, y_train)
df = pd.DataFrame.from_dict(sfs.get_metric_dict()).T
df.head(df.shape[0])
| feature_idx | cv_scores | avg_score | feature_names | ci_bound | std_dev | std_err | |
|---|---|---|---|---|---|---|---|
| 1 | (5,) | [0.8181818181818182, 0.7482517482517482, 0.753... | 0.787935 | (Sex=male,) | 0.040774 | 0.031724 | 0.015862 |
| 2 | (2, 5) | [0.8181818181818182, 0.7622377622377622, 0.746... | 0.79214 | (SibSp, Sex=male) | 0.043685 | 0.033989 | 0.016994 |
| 3 | (0, 2, 5) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.799153 | (Pclass, SibSp, Sex=male) | 0.039486 | 0.030721 | 0.015361 |
| 4 | (0, 2, 3, 5) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.799153 | (Pclass, SibSp, Parch, Sex=male) | 0.039486 | 0.030721 | 0.015361 |
| 5 | (0, 2, 3, 5, 9) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.800561 | (Pclass, SibSp, Parch, Sex=male, Embarked=Q) | 0.040679 | 0.03165 | 0.015825 |
| 6 | (0, 2, 3, 5, 9, 11) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.800561 | (Pclass, SibSp, Parch, Sex=male, Embarked=Q, N... | 0.040679 | 0.03165 | 0.015825 |
| 7 | (0, 2, 3, 5, 9, 11, 12) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.800561 | (Pclass, SibSp, Parch, Sex=male, Embarked=Q, N... | 0.040679 | 0.03165 | 0.015825 |
| 8 | (0, 2, 3, 5, 9, 11, 12, 13) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.800561 | (Pclass, SibSp, Parch, Sex=male, Embarked=Q, N... | 0.040679 | 0.03165 | 0.015825 |
import matplotlib.pyplot as plt
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs
plot_sfs(sfs.get_metric_dict(), kind="std_dev")
plt.title("Sequential Forward Selection (StdDev)")
plt.grid()
plt.show()

Описанный выше подход довольно быстрый: в нем столько итераций, сколько признаков в выборке. Но при этом он слишком жадный: перебирается слишком мало вариантов, и мы можем оказаться в плохой локальной точке. Процедуру можно усложнить. Один из подходов к усложнению — это алгоритм ADD-DEL, который не только добавляет, но и удаляет признаки из оптимального множества.
Алгоритм начинается с процедуры жадного добавления. Множество признаков наращивается до тех пор, пока получается уменьшить ошибку, затем признаки жадно удаляются из подмножества, то есть перебираются все возможные варианты удаления признака, оценивается ошибка и удаляется тот признак, который приводит к наибольшему уменьшению ошибки на выборке. Эта процедура повторяет добавление и удаление признаков до тех пор, пока уменьшается ошибка. Алгоритм ADD-DEL всё еще жадный, но при этом он менее жадный, чем предыдущий, поскольку может исправлять ошибки, сделанные в начале перебора: если вначале был добавлен неинформативный признак, то на этапе удаления от него можно избавиться.

sffs = SequentialFeatureSelector(
LogisticRegression(max_iter=1000), # represents the classifier
k_features=8, # the number of features you want to select
forward=True, # add features
floating=True, # remove features
scoring="accuracy", # means that the selection will be decided by the accuracy of the classifier.
cv=KFold(n_splits=5, shuffle=True, random_state=42),
)
sffs.fit(x_train.values, y_train) # performs the actual SFFS algorithm
df = pd.DataFrame.from_dict(sffs.get_metric_dict()).T
df.head(df.shape[0])
| feature_idx | cv_scores | avg_score | feature_names | ci_bound | std_dev | std_err | |
|---|---|---|---|---|---|---|---|
| 1 | (5,) | [0.8181818181818182, 0.7482517482517482, 0.753... | 0.787935 | (5,) | 0.040774 | 0.031724 | 0.015862 |
| 2 | (2, 5) | [0.8181818181818182, 0.7622377622377622, 0.746... | 0.79214 | (2, 5) | 0.043685 | 0.033989 | 0.016994 |
| 3 | (0, 2, 5) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.799153 | (0, 2, 5) | 0.039486 | 0.030721 | 0.015361 |
| 4 | (0, 2, 3, 5) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.799153 | (0, 2, 3, 5) | 0.039486 | 0.030721 | 0.015361 |
| 5 | (0, 2, 3, 5, 9) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.800561 | (0, 2, 3, 5, 9) | 0.040679 | 0.03165 | 0.015825 |
| 6 | (0, 2, 3, 5, 9, 11) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.800561 | (0, 2, 3, 5, 9, 11) | 0.040679 | 0.03165 | 0.015825 |
| 7 | (0, 2, 5, 9, 11, 12, 13) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.80197 | (0, 2, 5, 9, 11, 12, 13) | 0.042151 | 0.032795 | 0.016398 |
| 8 | (0, 2, 5, 9, 11, 12, 13, 15) | [0.8181818181818182, 0.7832167832167832, 0.746... | 0.80197 | (0, 2, 5, 9, 11, 12, 13, 15) | 0.042151 | 0.032795 | 0.016398 |
plot_sfs(sffs.get_metric_dict(), kind="std_dev")
plt.title("Sequential Forward Selection (StdDev)")
plt.grid()
plt.show()
Использование весов признаков
Во многих моделях (например, в линейных) перед признаками стоят веса. Если признаки масштабированы, то веса при признаках можно интерпретировать как информативности: чем больше по модулю вес при признаке $j$, тем больший вклад этот признак вносит в ответ модели. Однако если признаки не масштабированы, то так использовать веса уже нельзя. Например, если есть два признака, и один по масштабу в 1000 раз меньше другого, то вес первого признака может быть очень большим, только чтобы признаки были одинаковыми по масштабу. Если необходимо обнулить как можно больше весов, чтобы линейная модель учитывала только те признаки, которые наиболее важны для нее, можно использовать L1-регуляризацию. Чем больше коэффициент при L1-регуляризаторе, тем меньше признаков будет использовать линейная модель.
Рассмотрим это на примере Линейного классификатора, который мы конструировали на 2-м занятии.

$\boldsymbol{w} \cdot \boldsymbol{x} = w_0 \cdot x_0 + w_1 \cdot x_1 + \cdots + w_{n-1} \cdot x_{n-1} = 1\times1 + 2\times0 + (-1)\times4 + 0\times(-2) = -3$
lr = LogisticRegression(max_iter=1000)
lr.fit(x_train, y_train)
df = pd.DataFrame(lr.coef_[0], x_train.columns, columns=["Coef"]).sort_values(
"Coef", key=abs, ascending=False
)
df.head(df.shape[0])
| Coef | |
|---|---|
| Sex=female | 1.347877 |
| Sex=male | -1.335789 |
| Cabin_char=E | 0.852875 |
| Cabin_char=F | 0.842839 |
| Cabin_char=G | -0.637927 |
| Cabin_char=C | -0.557529 |
| Pclass | -0.538057 |
| N_cabins | -0.494651 |
| Cabin_char=n | -0.392910 |
| Cabin_char=D | 0.378228 |
| Cabin_char=T | -0.308945 |
| SibSp | -0.303337 |
| Cabin_char=A | -0.287940 |
| Embarked=C | 0.216808 |
| Embarked=S | -0.203422 |
| Embarked=Q | -0.131855 |
| Cabin_char=B | 0.123397 |
| sqrt_Fare | 0.110342 |
| Parch | -0.107805 |
| Age | -0.010998 |
| Cabin_num | 0.002733 |
from sklearn.feature_selection import SelectFromModel
# 1. A SelectFromModel instance selects the features
# whose coefficients are non-zero when the feature is included in the model.
# 2. The LogisticRegression instance runs the logistic regression
# algorithm on the training data.
# selecting features based on importance weights
lr_selector = SelectFromModel(LogisticRegression(max_iter=1000))
lr_selector.fit(x_train, y_train)
SelectFromModel(estimator=LogisticRegression(max_iter=1000))In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
SelectFromModel(estimator=LogisticRegression(max_iter=1000))
LogisticRegression(max_iter=1000)
LogisticRegression(max_iter=1000)
x_train.columns[lr_selector.get_support()] # Get a mask of the features selected
Index(['Pclass', 'Sex=male', 'Sex=female', 'N_cabins', 'Cabin_char=F',
'Cabin_char=G', 'Cabin_char=C', 'Cabin_char=E'],
dtype='object')
lr_selector.transform(x_train) # select only relevant features
array([[1., 1., 0., ..., 0., 1., 0.],
[2., 1., 0., ..., 0., 0., 0.],
[3., 1., 0., ..., 0., 0., 0.],
...,
[3., 1., 0., ..., 0., 0., 0.],
[1., 0., 1., ..., 0., 0., 0.],
[1., 1., 0., ..., 0., 0., 0.]])
from sklearn.ensemble import RandomForestClassifier
# select features with RFC
rf = RandomForestClassifier(n_estimators=500, random_state=42)
rf_selector = SelectFromModel(rf)
rf_selector.fit(x_train, y_train) # Fit it on the training data
x_train.columns[rf_selector.get_support()]
Index(['Pclass', 'Age', 'sqrt_Fare', 'Sex=male', 'Sex=female', 'Cabin_num'], dtype='object')
Для определения важности признака можно перемешать его значения. Это не изменит форму распределения признака, но сделает его бессмысленным. По падению качества модели мы можем оценить, каков был вклад признака до изменения: если качество упало сильно, то он был значимым.
В sklearn это реализовано как отдельный класс permutation_importance.
Изменение качества модели рассчитывается на OOB (Out-of-bag samples) объектах: на объектах, которые не вошли в обучающую выборку, а остались для валидации (не путать с тестовой выборкой, которую мы не трогаем).
У данного метода есть три особенности:
permutation_importance имеет параметр n_repeats, который определяет, сколько раз признак будет перемешиваться случайным образом.Когда два признака сильно коррелированы и мы перемешали один из них, линейная модель сохранит информацию о перемешанном признаке через коррелированный с ним, что может привести к занижению важности.
[Doc sklearn] Misleading values on strongly correlated features
С другой стороны, может произойти обратный эффект. Дерево решений пытается разбить пространство плоскостями, и в областях, где объектов нет, оно, можно сказать, занимается угадыванием. Если $x_1$ и $x_2$ на картинке ниже линейно зависимы, то не может возникнуть ситуация, при которой $x_1 = 0$, а $x_2 = 1$. А как раз при перемешивании такая ситуация возникнет, и точки начнут попадать в "проблемные" области, в которых дерево решений плохо предсказывает. В результате получаем завышенную важность.
Для борьбы с неадекватной оценкой коррелированных признаков можно собирать коррелированные признаки в кластеры и оставить только один признак для каждого кластера.
Одна из вариаций permutation importance подразумевает обучение модели заново после каждого перемешивания признаков. Это дает чуть более адекватную оценку важности, но очень долго.
Сделаем permutation importance:
from sklearn.inspection import permutation_importance
model = RandomForestClassifier(n_estimators=500, random_state=42)
model.fit(x_train, y_train)
r = permutation_importance(model, x_test, y_test, n_repeats=100, random_state=42)
df = pd.DataFrame({"name": x_train.columns, "imp": r.importances_mean}).sort_values(
"imp", ascending=False
)
df
| name | imp | |
|---|---|---|
| 6 | Sex=female | 0.048994 |
| 5 | Sex=male | 0.023240 |
| 0 | Pclass | 0.022514 |
| 4 | sqrt_Fare | 0.022291 |
| 1 | Age | 0.010447 |
| 3 | Parch | 0.010223 |
| 16 | Cabin_char=E | 0.009609 |
| 7 | Embarked=C | 0.002626 |
| 2 | SibSp | 0.002235 |
| 8 | Embarked=S | 0.001844 |
| 20 | Cabin_char=D | 0.001229 |
| 12 | Cabin_char=T | 0.000000 |
| 13 | Cabin_char=F | -0.000056 |
| 14 | Cabin_char=G | -0.000223 |
| 11 | N_cabins | -0.000279 |
| 9 | Embarked=Q | -0.000782 |
| 17 | Cabin_char=B | -0.000838 |
| 15 | Cabin_char=C | -0.005978 |
| 18 | Cabin_char=A | -0.015698 |
| 10 | Cabin_num | -0.016536 |
| 19 | Cabin_char=n | -0.016927 |
import seaborn as sns
plt.figure(figsize=(8, 8))
sns.barplot(data=df, y="name", x="imp", color="blue", orient="h")
plt.show()
Ниже выполняются те же операции, но уже с линейной регрессией.
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x_train, y_train)
r = permutation_importance(model, x_test, y_test, n_repeats=100, random_state=42)
df = pd.DataFrame({"name": x_train.columns, "imp": r.importances_mean}).sort_values(
"imp", ascending=False
)
df
| name | imp | |
|---|---|---|
| 5 | Sex=male | 0.111689 |
| 6 | Sex=female | 0.111689 |
| 0 | Pclass | 0.059201 |
| 1 | Age | 0.023061 |
| 4 | sqrt_Fare | 0.015694 |
| 20 | Cabin_char=D | 0.009864 |
| 2 | SibSp | 0.008806 |
| 16 | Cabin_char=E | 0.007650 |
| 13 | Cabin_char=F | 0.004585 |
| 8 | Embarked=S | 0.002909 |
| 10 | Cabin_num | 0.001179 |
| 19 | Cabin_char=n | 0.001033 |
| 3 | Parch | 0.000848 |
| 9 | Embarked=Q | 0.000727 |
| 17 | Cabin_char=B | 0.000485 |
| 15 | Cabin_char=C | 0.000005 |
| 12 | Cabin_char=T | 0.000000 |
| 7 | Embarked=C | -0.000649 |
| 18 | Cabin_char=A | -0.000721 |
| 11 | N_cabins | -0.003324 |
| 14 | Cabin_char=G | -0.005103 |
plt.figure(figsize=(8, 8))
sns.barplot(data=df, y="name", x="imp", color="blue", orient="h")
plt.show()
Как видно, у некоторых признаков при переходе от древесных моделей к линейным значительно повысилась важность, что говорит об их скоррелированности.
Boruta развивает идею Permutation.
Попробуем "раздуть" наш датасет, добавив в него "теневые признаки" $-$ перемешанные реальные. Таким образом, наш датасет точно будет содержать хорошие признаки (мы ничего не удаляем).

После этого обучаем модель и отбираем те признаки, чей feature_importance больше, чем у лучшего из теневых. Успех? Не совсем, ведь перемешивание это случайный процесс. Надо повторить процедуру несколько раз для того чтобы удалить случайные скачки качества.
Таким образом, для каждого признака мы будем знать, сколько раз мы его отобрали. Получаем распределение. Самая большая неопределенность будет в середине (вероятность отобрать = 0.5):

Набор (в нашем случае из 20) испытаний Бернулли это биномиальное распределение. Поступаем просто. Со значимостью, допустим 0.05, берем все из хорошего хвоста и отбрасываем из плохого хвоста. С признаками из середины колокола ничего особо не сделаешь, увеличение числа итераций приведет к ужатию колокола, но глобально не поможет.
Если нам нужна хорошо интерпретируемая модель, то надо брать только "точно хорошие" признаки. А если мы готовы поднабрать мусорных признаков, то можем отбросить только плохой хвост.
Будем использовать реализацию github boruta_py. Возьмем Random Forest модель.
model = RandomForestClassifier(n_estimators=500, random_state=42)
model.fit(x_train, y_train)
RandomForestClassifier(n_estimators=500, random_state=42)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
RandomForestClassifier(n_estimators=500, random_state=42)
Попробуем применить алгоритм Boruta к этому же датасету, и сократить количество признаков. Оценим текущее качество модели, используя ROC-AUC
pred = model.predict_proba(x_test)[:, 1]
r1 = roc_auc_score(y_score=pred, y_true=y_test)
print(f"ROC-AUC: {r1:.4f}")
ROC-AUC: 0.8894
Загрузим Boruta:
!pip install -q boruta
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 56.6/56.6 kB 5.6 MB/s eta 0:00:00
Питоновская реализация Boruta соответствует API sklearn и может использоваться как в конвейере, так и самостоятельно.
Boruta работает с numpy.array, поэтому используем .values() :
print(type(x_train))
print(type(x_train.values))
<class 'pandas.core.frame.DataFrame'> <class 'numpy.ndarray'>
Проведем оценку признаков при помощи Boruta.
from boruta import BorutaPy
# define Boruta feature selection method
model = RandomForestClassifier(n_estimators=500, random_state=42)
feat_selector = BorutaPy(model, n_estimators=100, verbose=2, random_state=42)
# find all relevant features
feat_selector.fit(x_train.values, y_train.values)
Iteration: 1 / 100 Confirmed: 0 Tentative: 21 Rejected: 0 Iteration: 2 / 100 Confirmed: 0 Tentative: 21 Rejected: 0 Iteration: 3 / 100 Confirmed: 0 Tentative: 21 Rejected: 0 Iteration: 4 / 100 Confirmed: 0 Tentative: 21 Rejected: 0 Iteration: 5 / 100 Confirmed: 0 Tentative: 21 Rejected: 0 Iteration: 6 / 100 Confirmed: 0 Tentative: 21 Rejected: 0 Iteration: 7 / 100 Confirmed: 0 Tentative: 21 Rejected: 0 Iteration: 8 / 100 Confirmed: 3 Tentative: 1 Rejected: 17 Iteration: 9 / 100 Confirmed: 3 Tentative: 1 Rejected: 17 Iteration: 10 / 100 Confirmed: 3 Tentative: 1 Rejected: 17 Iteration: 11 / 100 Confirmed: 3 Tentative: 1 Rejected: 17 Iteration: 12 / 100 Confirmed: 3 Tentative: 0 Rejected: 18 BorutaPy finished running. Iteration: 13 / 100 Confirmed: 3 Tentative: 0 Rejected: 18
BorutaPy(estimator=RandomForestClassifier(random_state=RandomState(MT19937) at 0x7ABE867D0F40),
n_estimators=100, random_state=RandomState(MT19937) at 0x7ABE867D0F40,
verbose=2)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. BorutaPy(estimator=RandomForestClassifier(random_state=RandomState(MT19937) at 0x7ABE867D0F40),
n_estimators=100, random_state=RandomState(MT19937) at 0x7ABE867D0F40,
verbose=2)RandomForestClassifier(random_state=RandomState(MT19937) at 0x7ABE867D0F40)
RandomForestClassifier(random_state=RandomState(MT19937) at 0x7ABE867D0F40)
Выведем признаки с оценкой их важности и очистим датасет от маловажных признаков
# zip my names, ranks, and decisions in a single iterable
feature_ranks = list(
zip(x_train.columns, feat_selector.ranking_, feat_selector.support_)
)
# iterate through print out the results and remove features with low rank
for feat in feature_ranks:
print("Feature: {:<25} Rank: {}, Keep: {}".format(feat[0], feat[1], feat[2]))
if feat[2] == False:
del x_train[feat[0]]
Feature: Pclass Rank: 3, Keep: False Feature: Age Rank: 2, Keep: False Feature: SibSp Rank: 5, Keep: False Feature: Parch Rank: 6, Keep: False Feature: sqrt_Fare Rank: 1, Keep: True Feature: Sex=male Rank: 1, Keep: True Feature: Sex=female Rank: 1, Keep: True Feature: Embarked=C Rank: 9, Keep: False Feature: Embarked=S Rank: 8, Keep: False Feature: Embarked=Q Rank: 11, Keep: False Feature: Cabin_num Rank: 4, Keep: False Feature: N_cabins Rank: 15, Keep: False Feature: Cabin_char=T Rank: 19, Keep: False Feature: Cabin_char=F Rank: 16, Keep: False Feature: Cabin_char=G Rank: 18, Keep: False Feature: Cabin_char=C Rank: 13, Keep: False Feature: Cabin_char=E Rank: 11, Keep: False Feature: Cabin_char=B Rank: 11, Keep: False Feature: Cabin_char=A Rank: 17, Keep: False Feature: Cabin_char=n Rank: 7, Keep: False Feature: Cabin_char=D Rank: 14, Keep: False
Boruta из 21 признака оставила нам только три: sqrt_Fare , Sex=male , Sex=female
x_train
| sqrt_Fare | Sex=male | Sex=female | |
|---|---|---|---|
| 331 | 5.338539 | 1 | 0 |
| 733 | 3.605551 | 1 | 0 |
| 382 | 2.815138 | 1 | 0 |
| 704 | 2.802535 | 1 | 0 |
| 813 | 5.592406 | 0 | 1 |
| ... | ... | ... | ... |
| 106 | 2.765863 | 0 | 1 |
| 270 | 5.567764 | 1 | 0 |
| 860 | 3.756102 | 1 | 0 |
| 435 | 10.954451 | 0 | 1 |
| 102 | 8.791331 | 1 | 0 |
712 rows × 3 columns
Обучим алгоритм на признаках, отобранных Boruta. Давайте проверим, можем ли мы добиться такого же результата, если проанализируем и уберем «лишние» данные?
# Build the model with the random forest algorithm
model = RandomForestClassifier(n_estimators=500, random_state=42)
model.fit(x_train, y_train)
pred = model.predict_proba(x_test[x_train.columns])[:, 1]
r1 = roc_auc_score(y_score=pred, y_true=y_test)
print(f"ROC-AUC: {r1:.4f}")
ROC-AUC: 0.8243
После удаления ~85% признаков качество упало на так сильно, как можно было бы ожидать.
Редко используемый метод, заключающийся в том, что мы просто выбрасываем переменную и смотрим, как упало качество по сравнению с "полной" моделью.
Это не очень хорошо как минимум потому, что многие гиперпараметры зависят от числа признаков $-$ модель будет работать хуже еще и поэтому. Опять же между признаками могут быть сложные взаимодействия.
Никогда не отбирайте признаки на том же наборе данных, на котором тестируетесь. Иначе получите завышенное качество вашей модели.
Сгенерируем следующий датасет.
У нас есть по 500 пациентов, больных и здоровых. Для каждого известно 100000 случайных бинарных признаков. Что будет, если мы попросим нашу модель научиться отделять здоровых от больных?
np.random.seed(42)
pat_cnt = 500 # patients
snv_count = 100000 # all features(binary)
genes = [f"SNP{ind}" for ind in range(snv_count)] # features names
# Generate 2 data sets, healthy and diseased patients.
# Each data set is a binary vector of length `snv_count`,
# in other words a SNV count vector of length 100000.
genes = [f"SNP{ind}" for ind in range(snv_count)]
healthy = pd.DataFrame(
np.random.choice([0, 1], size=(pat_cnt, snv_count)), columns=genes
)
# We add a `State` column, indicating whether it's healthy or diseased.
healthy["State"] = "H"
diseased = pd.DataFrame(
np.random.choice([0, 1], size=(pat_cnt, snv_count)), columns=genes
)
diseased["State"] = "D"
patients = pd.concat([healthy, diseased], axis=0)
# We drop the State column to get a `x` and a `y` matrix.
x = patients.drop("State", axis=1)
y = patients["State"]
x.head()
| SNP0 | SNP1 | SNP2 | SNP3 | SNP4 | SNP5 | SNP6 | SNP7 | SNP8 | SNP9 | ... | SNP99990 | SNP99991 | SNP99992 | SNP99993 | SNP99994 | SNP99995 | SNP99996 | SNP99997 | SNP99998 | SNP99999 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ... | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | ... | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | ... | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ... | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 4 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | ... | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
5 rows × 100000 columns
from sklearn.metrics import average_precision_score, accuracy_score
# 1. Split the data into train and test sets
x_train, x_test, y_train, y_test = train_test_split(
x, y == "D", test_size=0.3, random_state=42
)
# 2. Train a logistic regression model on the train set
model = LogisticRegression(max_iter=1000)
model.fit(x_train, y_train)
# 3. Predict the probabilities for train and test sets
# 4. Calculate ROCAUC and PRAUC scores for the prediction of train and test sets
# 5. Compare the performance of the model on train and test sets using the scores
y_train_pred = model.predict_proba(x_train)[:, 1]
train_rocauc = roc_auc_score(y_score=y_train_pred, y_true=y_train)
train_prauc = average_precision_score(y_score=y_train_pred, y_true=y_train)
train_accuracy = accuracy_score(y_pred=y_train_pred > 0.5, y_true=y_train)
print("Train quality:")
print(f"ROCAUC : {train_rocauc:.02f}")
print(f"PRAUC : {train_prauc:.02f}")
print(f"Accuracy: {train_accuracy:.02f}")
# Test
y_test_pred = model.predict_proba(x_test)[:, 1]
test_rocauc = roc_auc_score(y_score=y_test_pred, y_true=y_test)
test_prauc = average_precision_score(y_score=y_test_pred, y_true=y_test)
test_accuracy = accuracy_score(y_pred=y_test_pred > 0.5, y_true=y_test)
print("\nTest quality:")
print(f"ROCAUC : {test_rocauc:.02f}")
print(f"PRAUC : {test_prauc:.02f}")
print(f"Accuracy: {test_accuracy:.02f}")
Train quality: ROCAUC : 1.00 PRAUC : 1.00 Accuracy: 1.00 Test quality: ROCAUC : 0.49 PRAUC : 0.52 Accuracy: 0.48
Модель идеально выучила данные обучения, но с тестом беда (как и должно быть)
Возьмем те признаки, для которых средняя разница для больных и здоровых максимальна. Заметьте, мы даже не используем чего-то сильно сложного.
# 1. Take the mean of all the reads for each gene in healthy
# and each gene in diesised.
# 2. Subtract the mean number of reads for each gene in diesised
# from the mean number of reads for each gene in healthy.
diffs = x[y == "H"].mean(axis=0) - x[y == "D"].mean(axis=0)
# 3. Look at the top k most different genes
# by sorting the values in the resulting array from largest to smallest.
top = np.abs(diffs).sort_values(ascending=False)[0:10]
genes = top.index
# Print the gene names of the top k genes.
print("Genes", genes)
# Select x
x_selected = x[genes]
Genes Index(['SNP3660', 'SNP54022', 'SNP96099', 'SNP77184', 'SNP71144', 'SNP70126',
'SNP14768', 'SNP63912', 'SNP17706', 'SNP32249'],
dtype='object')
И посмотрим на качество модели:
# 1. Split the data into train and test sets
x_train, x_test, y_train, y_test = train_test_split(
x_selected, y == "D", test_size=0.3, random_state=42
)
# 2. Train a logistic regression model on the train set
model = LogisticRegression()
model.fit(x_train, y_train)
# 3. Predict the probabilities for train and test sets
# 4. Calculate ROCAUC and PRAUC scores for the prediction of train and test sets
# 5. Compare the performance of the model on train and test sets using the scores
y_train_pred = model.predict_proba(x_train)[:, 1]
train_rocauc = roc_auc_score(y_score=y_train_pred, y_true=y_train)
train_prauc = average_precision_score(y_score=y_train_pred, y_true=y_train)
train_accuracy = accuracy_score(y_pred=y_train_pred > 0.5, y_true=y_train)
print("Train quality:")
print(f"ROCAUC : {train_rocauc:.02f}")
print(f"PRAUC : {train_prauc:.02f}")
print(f"Accuracy: accuracy {train_accuracy:.02f}")
# Test
y_test_pred = model.predict_proba(x_test)[:, 1]
train_rocauc = roc_auc_score(y_score=y_test_pred, y_true=y_test)
train_prauc = average_precision_score(y_score=y_test_pred, y_true=y_test)
train_accuracy = accuracy_score(y_pred=y_test_pred > 0.5, y_true=y_test)
print("\nTest quality:")
print(f"ROCAUC : {train_rocauc:.02f}")
print(f"PRAUC : {train_prauc:.02f}")
print(f"Accuracy: accuracy {train_accuracy:.02f}")
Train quality: ROCAUC : 0.72 PRAUC : 0.71 Accuracy: accuracy 0.67 Test quality: ROCAUC : 0.72 PRAUC : 0.70 Accuracy: accuracy 0.65
Внезапно качество на тесте выглядит разумным. Да, не очень классное, но есть. А должно быть соответствующее случайной модели — признаки-то случайные.
Дело в том, что мы изначально выбрали те признаки, которые работали хорошо по случайным причинам на всем нашем искусственном датасете, а не только на тренировочной выборке.
# Split the data into train and test sets (with two sizes)
x_fs_train, x_test, y_fs_train, y_test = train_test_split(
x, y == "D", test_size=0.3, random_state=42
)
# split again
x_fs, x_train, y_fs, y_train = train_test_split(
x_fs_train, y_fs_train, test_size=0.8, random_state=42
)
Отбираем признаки на одном датасете
# 1. Find the difference between the mean expression
# of the genes
# 2. Sort the resulting list according to the difference in means
# (from greatest difference to least)
# 3. Take the top K genes and return them
diffs = x_fs[np.logical_not(y_fs)].mean(axis=0) - x_fs[y_fs].mean(axis=0)
top = np.abs(diffs).sort_values(ascending=False)[0:10]
genes = top.index
Обучаем модель на втором
model = LogisticRegression()
model.fit(x_train[genes], y_train)
y_train_pred = model.predict_proba(x_train[genes])[:, 1]
y_train_pred = model.predict_proba(x_train[genes])[:, 1]
train_rocauc = roc_auc_score(y_score=y_train_pred, y_true=y_train)
train_prauc = average_precision_score(y_score=y_train_pred, y_true=y_train)
train_accuracy = accuracy_score(y_pred=y_train_pred > 0.5, y_true=y_train)
print("Train quality:")
print(f"ROCAUC : {train_rocauc:.02f}")
print(f"PRAUC : {train_prauc:.02f}")
print(f"Accuracy: accuracy {train_accuracy:.02f}")
Train quality: ROCAUC : 0.57 PRAUC : 0.56 Accuracy: accuracy 0.56
Тестируем на третьем
y_test_pred = model.predict_proba(x_test[genes])[:, 1]
train_rocauc = roc_auc_score(y_score=y_test_pred, y_true=y_test)
train_prauc = average_precision_score(y_score=y_test_pred, y_true=y_test)
train_accuracy = accuracy_score(y_pred=y_test_pred > 0.5, y_true=y_test)
print("Test quality:")
print(f"ROCAUC : {train_rocauc:.02f}")
print(f"PRAUC : {train_prauc:.02f}")
print(f"Accuracy: {train_accuracy:.02f}")
Test quality: ROCAUC : 0.52 PRAUC : 0.50 Accuracy: 0.52
Часто мы хотим данные из пространства высокой размерности преобразовать в пространство более низкой размености с сохранением одного или нескольких свойств, например:
Зачем это нужно? По многим причинам:
Многие алгоритмы показывают себя плохо на пространствах большой размерности в принципе (проклятие размерности).
Некоторые просто будут значительно дольше работать, при этом качество их работы не изменится от уменьшения размерности.
Понижение размерности позволяет использовать память более эффективно и подавать модели на обучение за один раз больше объектов.
Избавиться от шумовых признаков, обсудим это дальше.
Задача визуализации: хочется взглянуть на наши объекты, а делать это в 100-мерном или 100000-мерном пространстве невозможно.
Удаление выбросов — в пространствах меньшей размерности можем их увидеть глазами.
Можем увидеть закономерности в данных: что они бьются на явные кластеры и т. д.
В машинном обучении часто используют предположение о многообразии (manifold assumption). Это предположение о том, что между признаками, описывающими реальные объекты, существуют некоторые нетривиальные связи. Вследствие этого данные заполняют не весь объем пространства признаков, а лежат на некоторой поверхности — на многообразии (manifold).
Если предположение верно, то каждый объект может быть достаточно точно описан новыми признаками в пространстве значительно меньшей размерности, чем исходное пространство признаков.
При этом мы будем терять часть информации об объектах. Но при выполнении предположения о многообразии (а оно почти всегда выполняется) и при правильных настройках алгоритма понижения размерности эти потери будут незначительны.

В большинстве случаев это действительно правда. Например, лица людей даже на фотографиях 300x300, очевидно, лежат в пространстве меньшей размерности, нежели 90000. Ведь не каждая матрица 300 на 300, заполненная какими-то значениями от 0 до 1, даст нам изображение человека.

Метод главных компонент (Principal Component Analysys, PCA) — простейший линейный метод снижения размерности, описан Пирсоном в 1901 году.
Идея заключается в преобразовании $D$ исходных признаков таким образом, чтобы получить $d$ признаков, содержащих как можно больше информации из исходных признаков:
$$\large z_{ij} = \sum^D_{k=1}w_{jk}x_{ik},$$где: $\; z_{ij}$ — новые признаки ($d$ штук),
$\qquad x_{ik}$ — исходные признаки ($D$ штук),
$\qquad w_{jk}$ — вклад исходного $k$-го признака в новый $j$-й.
Запишем линейное преобразование исходного признакового пространства в матричном виде.
Требование — ортогональность матрицы $W: W^TW = I$, где $I$ — единичная матрица.
Получение новых признаков $Z$ осуществляется домножением исходных признаков $X$ на матрицу $W: XW=Z$.
Следовательно, $X=ZW^T$
Задача: $\displaystyle ||X-ZW^T||^2 \rightarrow \min_{W}$
$$$$Рассмотрим простой пример для понимания интуиции, которая стоит за методом главных компонент.
У нас есть выборка объектов с двумя признаками $x_1$ и $x_2$, отобразим их на плоскости. Мы хотим, чтобы у нас был только один признак, который характеризует наши данные. Тогда наша задача — провести прямую через наши точки так, чтобы она наилучшим образом характеризовала наши данные

Проведем прямую вдоль максимального изменения данных и спроецируем точки на нее. Это и будет наша первая главная компонента.

Теперь мы можем использовать только один признак, который лежит на новой оси, а любые отклонения от нее это просто шум (в действительности, определить, что является шумом в данных это нетривиальная задача).

Это то, как можно понимать интуицию работы PCA.
В более многомерном случае (например, при количестве признаков 200) мы бы делали то же самое:

Чтобы понять, как использовать PCA на практике, найдем главные компоненты для датасета Titanic и посмотрим, как распределится между ними дисперсия.
import pandas as pd
import numpy as np
# The categorical-to-numerical function
# Changed to automatically add column names
def cat_to_num(data): # one-hot encoding
categories = set(data)
features = {}
for cat in categories:
binary = data == cat
if len(set(binary)) == 1:
# Ignore features where all values equal
continue
new_key = f"{data.name}={cat}"
features[new_key] = binary.astype("int")
return pd.DataFrame(features)
def cabin_features(data):
features = []
for cabin in data:
cabins = str(cabin).split(" ")
n_cabins = len(cabins)
# First char is the cabin_char
try:
cabin_char = cabins[0][0]
except IndexError:
cabin_char = "X"
n_cabins = 0
# The rest is the cabin number
try:
cabin_num = int(cabins[0][1:])
except:
cabin_num = -1
# Add 3 features for each passanger
features.append([cabin_char, cabin_num, n_cabins])
features = np.array(features)
dic_of_features = {
"Cabin_num": features[:, 1].astype("int"),
"N_cabins": features[:, 2].astype("int"),
}
out = pd.DataFrame(dic_of_features)
char_column = pd.DataFrame({"Cabin_char": features[:, 0]})
cabin_ch = cat_to_num(char_column["Cabin_char"])
return out.join(cabin_ch)
def prepare_data(data):
"""Takes a dataframe of raw data and returns ML model features"""
# Initially, we build a model only on the available numerical values
features = data.drop(
[
"PassengerId",
"Survived",
"Fare",
"Name",
"Sex",
"Ticket",
"Cabin",
"Embarked",
],
axis=1,
)
# Setting missing age values to -1
features["Age"] = data["Age"].fillna(-1)
# Adding the sqrt of the fare feature
features["sqrt_Fare"] = np.sqrt(data["Fare"])
# Adding gender categorical value
features = features.join(cat_to_num(data["Sex"]))
# Adding Embarked categorical value
features = features.join(cat_to_num(data["Embarked"]))
# Split cabin
features = features.join(cabin_features(data["Cabin"]))
return features
Загрузим датасет и подготовим данные
from sklearn.model_selection import train_test_split
# 1. Importing the data from the .csv
# 2. Pre-processing the data and creating a feature set
# 3. Splitting the data into training and test data and labels
dataset = pd.read_csv(
"https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/titanic.csv"
)
features = prepare_data(dataset)
x_train, x_test, y_train, y_test = train_test_split(
features, dataset["Survived"], test_size=0.2, random_state=42
)
Полезной информацией является коэффициент объясненной дисперсии (explained variance ratio) главной компоненты. Этот коэффициент является отношением между дисперсией главной компоненты и суммой дисперсий всех главных компонент. Он указывает долю выборочной дисперсии, которая лежит вдоль оси каждой главной компоненты.
В модуле PCA, после fit можно получить explained variance ratio посредством обращения к полю explained_variance_ratio_, а explained variance — посредством обращения к полю explained_variance_.
Построим график с explained_variance_ratio_ всех компонент
import sklearn
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# performing PCA with default number of principal components.
titanic_pca = sklearn.decomposition.PCA()
titanic_pca.fit(x_train) # fitting our PCA model with the training data.
# calculating the explained variance of each of the components.
evr = titanic_pca.explained_variance_ratio_
# We are plotting the explained variance ratios.
plt.bar(range(evr.shape[0]), evr)
plt.title("Variance by components")
plt.xlabel("Components")
plt.ylabel("Variance")
plt.show()
titanic_pca.explained_variance_.shape
(21,)
Из графика не совсем понятно, сколько компонент брать, резко доля объясняемой дисперсии меняется в районе 2-компоненты. Посмотрим, сколько компонент нужно модели
from sklearn.linear_model import LogisticRegression
# 1.The first thing we do is to fit a PCA model to the training set
# of the Titanic dataset with n components from 1 to 10.
# 2.We then fit a logistic regression model to the transformed training data
# and make predictions on the transformed test set.
for i in range(1, 11):
titanic_pca = sklearn.decomposition.PCA(n_components=i)
titanic_pca.fit(x_train)
x_train_reduced = titanic_pca.transform(x_train)
model = LogisticRegression(max_iter=1000)
model.fit(x_train_reduced, y_train)
x_test_reduced = titanic_pca.transform(x_test)
# prints the number of PCA components and the score
# for the corresponding model.
print("%i first components %.2f" % (i, model.score(x_test_reduced, y_test)))
1 first components 0.61 2 first components 0.62 3 first components 0.68 4 first components 0.68 5 first components 0.75 6 first components 0.78 7 first components 0.78 8 first components 0.79 9 first components 0.79 10 first components 0.79
Явно видим, что уже первых 7 компонент достаточно для достижения качества, которое далее не меняется. Почему же мы видим снижение уже после 2 компоненты?
Мы забыли сделать стандартизацию наших данных.
В нашем датасете переменные имеют совершенно разные масштабы. Из-за этого часть из них "перетегягивает" на себя всю дисперсию.
В результате по доле дисперсии судить о важности компонент нельзя.
Сделаем предварительно стандартизацию
# First, we import the StandardScaler module.
from sklearn.preprocessing import StandardScaler
# Next, we create a StandardScaler object called scaler by calling the
# StandardScaler() function.
scaler = StandardScaler()
# We then fit the scaling model to our training data.
x_train = scaler.fit_transform(x_train)
# We transform your test set by applying the same scaling model.
x_test = scaler.transform(x_test)
# performing PCA with default number of principal components.
titanic_pca = sklearn.decomposition.PCA()
titanic_pca.fit(x_train) # fitting our PCA model with the training data.
PCA()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
PCA()
В PCA.components_ лежат вектора главных компонент, которые располагаются там построчно (n_components, n_features).
titanic_pca.components_.shape
(21, 21)
Обратите внимание, что PCA упорядочивает собственные вектора. Это значит, что собственный вектор, соответствующий главной компоненте и, соответственно, имеющей максимальную дисперсию, будет находиться в первой строке.
# calculating the explained variance of each of the components.
evr = titanic_pca.explained_variance_ratio_
# We are plotting the explained variance ratios.
plt.bar(range(evr.shape[0]), evr)
plt.title("Variance by components")
plt.xlabel("Components")
plt.ylabel("Variance")
plt.show()
Теперь видим, что не только первые две компоненты дают вклад. Это происходит потому, что переменные с большим диапазоном значений не забивают остальные.
Правда, теперь и значимого спада в доле объясняемой дисперсии мы долго не видим, поэтому встает вопрос: как выбрать число компонент так, чтобы взять нужное и отсечь ненужное?
Скачаем датасет, на котором польза от понижения размерности видна более явно.
В данном датасете хранятся признаки (нам сейчас не важно, какие), характеризующие примерно 8000 клеток крови.
# 1. Reading in the scRNAseq data.
scRNAseq = pd.read_csv(
"https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/scRNAseq_CITEseq.txt",
sep="\t",
)
x_scRNAseq = scRNAseq.iloc[:, 0:-1] # features
y_scRNAseq = scRNAseq.iloc[:, -1] # labels
# 2. taking the log of the data.
x_scRNAseq = np.log(x_scRNAseq + 1)
print(f"dataset shape: {scRNAseq.shape}")
dataset shape: (8617, 977)
Подбирать число компонент можно по-разному
Часто берут минимальное число компонент, которое объясняет 95% дисперсии. Подход, очевидно, порочный (а почему не 90% или 99%), зато быстрый.
# 1. We're calculating the explained variance ratio for
# each component of the PCA.
# 2. We're plotting these ratios in a chart.
pca = PCA(n_components=x_train.shape[1])
pca.fit(x_train)
ths = 0.95
total_explained = np.cumsum(pca.explained_variance_ratio_)
plt.figure(figsize=(6, 6))
plt.plot(np.arange(1, total_explained.shape[0] + 1), total_explained)
plt.axhline(xmin=0, xmax=1000, y=ths, c="red", ls="--")
chosen_number = np.where(total_explained >= 0.95)[0][0] + 1
plt.axvline(x=chosen_number, ymin=0, ymax=ths, c="red", ls="--")
plt.xticks(np.arange(1, x_train.shape[1]))
plt.ylabel("total sum of proportion of the explained variance")
plt.xlabel("Num of components", size=14)
plt.show()
Взяли 15 компонент. Почему именно столько? Почему не 16?
Непонятно. Просто, ибо поставили такой порог. Могли поставить и другой, и тогда бы взяли больше или меньше компонент.
Можно построить график, отражающий, сколько дисперсии объясняет каждая из компонент, и на основе графика выбрать нужное число компонент.
Идея подхода простая: переход от компонент, объясняющих что-то важное в данных, к компонентам, объясняющим шум, должен сопровождаться резким снижением доли объясняемой дисперсии.
Или можно сказать иначе: выбранные нами компоненты должны быть устойчивы к добавлению шума в данные. Если мы нашли резкий скачок в доле объясняемой дисперсии, то маловероятно, что добавление шума этот скачок нивелирует — наш способ отбора компонент устойчив к шуму.
В идеальном случае график будет выглядеть как-то так. Но на практике таких склонов может не быть, а может быть несколько.

# 1. First, we create a PCA object that you fit to the training data.
# 2. Then, we create a a scatter plot where we plot the explained
# variance ratio as a function of the number of PCA components.
# 3. We also plot the explained variance ratio as a function of the
# number of components, but with a smooth curve.
# 4. Finally, we show the plot.
n_comp = x_train.shape[1]
explained = pca.explained_variance_ratio_
plt.figure(figsize=(6, 6))
plt.scatter(np.arange(1, n_comp + 1), explained)
plt.plot(np.arange(1, n_comp + 1), explained)
plt.title("Dependence of variance on the number of components", size=14)
plt.xlabel("Num of components", size=14)
plt.ylabel("proportion of the explained variance", size=14)
plt.xticks(np.arange(1, x_train.shape[1]))
plt.show()
Понять, какое число компонент стоит выбрать, из такого графика сложно. Наверно, стоит выбрать последний склон — в нашем случае мы возьмем первые 12 компонент.
Можно применить критерий локтя и к нашему изначальному графику с суммарной долей объясненной дисперсии (в таком случае ожидаем скачок). Но там скачок также трудно обнаружить.
Еще одним способом выбрать число главных компонент является перестановочный метод. Он заключается в следующем:
1) Перемешиваем значения каждого признака.
2) Получаем матрицу признаков, которая не содержит никакой информации об исходном многообразии.
3) Делаем PCA.
4) Любая explained variance — просто из-за природы данных.
5) Делаем так 100-1000 раз.
6) Пусть на реальных данных k-я компонента объясняет n% дисперсии.
7) Смотрим на распределение доли дисперсии, объясняемой k-компонентой для случайных данных (полученных перемешиванием).
8) Можем сравнить и принять решение, объясняет ли k-я компонента что-то реальное или является просто шумом.
from tqdm import tqdm
from scipy.stats import norm
def shuffle_dataset(dataset):
random_data = {}
for col in dataset.columns:
random_data[col] = np.random.permutation(dataset.loc[:, col].values)
random_data = pd.DataFrame(random_data)
return random_data
def get_variance_by_chance(dataset, n_replics, n_components):
variance_explained_by_chance = np.zeros((n_replics, n_components))
for i in tqdm(range(n_replics)):
random_data = shuffle_dataset(dataset)
random_pca = PCA(n_components=n_components)
random_pca.fit(random_data)
variance_explained_by_chance[i, :] = random_pca.explained_variance_ratio_
return variance_explained_by_chance
def get_pc_variance(dataset, n_components):
pca = PCA(n_components=n_components)
pca.fit(dataset)
return pca.explained_variance_ratio_
def plot_mean_and_CI(
ax,
values,
label,
ci_level=0.95,
alpha_transparency=0.5,
color_mean=None,
color_shading=None,
):
mean = values.mean(axis=0)
std = values.std(axis=0)
n = values.shape[1]
se = std / np.sqrt(n)
q_alpha = (1 - ci_level) / 2
ci_num = np.abs(norm.ppf(q_alpha, loc=0, scale=1))
lb = mean - ci_num * se
ub = mean + ci_num * se
# plot the shaded range of the confidence intervals
ax.fill_between(
range(mean.shape[0]), ub, lb, color=color_shading, alpha=alpha_transparency
)
# plot the mean on top
ax.plot(mean, c=color_mean, lw=3, label=label)
def plot_explained_variance(ax, variance):
ax.plot(variance, label="real", lw=3)
ax.scatter(np.arange(0, variance.shape[0]), variance)
def plot_variance_by_change(ax, variance_by_chance):
plot_mean_and_CI(
ax, variance_by_chance, label="chance", color_mean="red", color_shading="red"
)
def calc_permutat_pval(real_values, permut_values, eps=None):
eps = eps or (1 / (permut_values.shape[0] * 10))
p_values = np.zeros_like(real_values)
for i in range(0, p_values.shape[0], 1):
p_values[i] = (permut_values[:, i] >= real_values[i]).mean() + eps
return p_values
def plot_explained_vs_chance(
ax, explained_variance, variance_by_chance, dataset_name, step=1
):
plot_explained_variance(ax, explained_variance)
plot_variance_by_change(ax, variance_by_chance)
ax.set_title(f"PCA {dataset_name}", size=25)
ax.set_xlabel("Component number", size=15)
ax.set_ylabel("Explained variance ration", size=15)
ax.set_xticks(np.arange(0, explained_variance.shape[0], step))
ax.set_xticklabels(np.arange(1, explained_variance.shape[0] + 1, step), size=10)
ax.tick_params(labelsize=10, size=8)
ax.set_ylim(0, explained_variance[0] + 0.1)
ax.legend(fontsize=15)
def plot_pval_plot(ax, p_values, dataset_name, alpha_level=0.05, logscale=True, step=1):
if logscale:
p_values = -np.log10(p_values)
alpha_level = -np.log10(alpha_level)
ax.set_title(f"PC significance, {dataset_name}", size=25)
ax.plot(p_values, lw=3)
ax.scatter(np.arange(0, p_values.shape[0]), p_values, lw=3)
ax.set_xlabel("Component number", size=15)
ax.set_ylabel("-log(pvalue + eps)", size=15)
ax.set_xticks(np.arange(0, p_values.shape[0], step))
ax.set_xticklabels(labels=np.arange(1, p_values.shape[0] + 1, step), size=10)
ax.tick_params(labelsize=10, size=8)
ax.hlines(
y=alpha_level,
xmin=0,
xmax=p_values.shape[0],
color="red",
linestyles="dashed",
lw=3,
)
def pca_analysis(ax1, ax2, dataset, title, n_components=None, n_replics=1000, step=1):
n_components = n_components or dataset.shape[1]
explained_variance = get_pc_variance(dataset, n_components)
variance_by_chance = get_variance_by_chance(dataset, n_replics, n_components)
p_values = calc_permutat_pval(explained_variance, variance_by_chance)
plot_explained_vs_chance(ax1, explained_variance, variance_by_chance, title)
plot_pval_plot(ax2, p_values, title)
np.random.seed(42)
f, (ax1, ax2) = plt.subplots(2, 1)
f.set_figheight(7)
f.set_figwidth(7)
plt.subplots_adjust(top=1.7)
pca_analysis(ax1, ax2, pd.DataFrame(x_train), "Titanic", n_replics=10, n_components=10)
100%|██████████| 10/10 [00:00<00:00, 114.46it/s]
Явно видим, что, согласно этому подходу, надо взять 6 компонент.
Мы можем также посмотреть, какие признаки внесли вклад в компоненты
first_component = titanic_pca.components_[0]
import seaborn as sns
sns.set_style("whitegrid")
plt.figure(figsize=(7, 7))
b = sns.barplot(
x=first_component,
y=features.columns,
orient="h",
hue=[z < 0 for z in first_component],
palette=["blue", "red"],
)
b.legend_.remove()
plt.show()
Или абсолютные вклады
plt.figure(figsize=(7, 7))
sns.barplot(x=np.abs(first_component), y=features.columns, orient="h", color="blue")
plt.show()
Видим, что наибольший вклад в дисперсию вносят такие признаки, как класс пассажира и класс кабины.
Сгенерируем абсолютно случайную выборку, в которой нет никакой внутренней структуры.
Но пусть у нас 5 признаков, описывающих выборку, пришли из стандартного нормально распределения, а еще один будет равновероятно принимать значение 0 и 3.
# 1. Generate x with N rows and P columns using the normal distribution.
# 2. Make a new vector with a third element that's either 0 or 3.
# 3. Append this vector to x, so that we now have a Nxp matrix.
np.random.seed(seed=42)
N = 200
P = 5
x = np.random.normal(size=[N, P])
print("x before", x.shape)
x = np.append(x, np.random.choice([0, 3], size=[N, 1]), axis=1)
print("x after", x.shape)
x before (200, 5) x after (200, 6)
# 1. Fitting PCA to the data, and reducing it to 2 components
# 2. Transforming that data using the PCA to get the low-dimensional representation
# 3. Plotting it with matplotlib
pca = PCA(2)
low_d = pca.fit_transform(x)
plt.figure(figsize=(7, 7))
plt.scatter(low_d[:, 0], low_d[:, 1])
plt.show()
Без предварительной нормализации мы получили два явных кластера в данных. Только вот кластеров этих по идее быть не должно
# 1. Normalize the data
# 2. Take the output from the PCA function and assign it to our variable low_d
# 3. Plot the first two components of low_d as a scatter plot.
x_scaled = StandardScaler().fit_transform(x)
low_d = pca.fit_transform(x_scaled)
plt.figure(figsize=(7, 7))
plt.scatter(low_d[:, 0], low_d[:, 1])
plt.show()
После стандартизации кластеры исчезли. Поэтому у вас должны быть весомые аргументы для того, чтобы не применять стандартизацию или другой метод, переводящий ваши данные в одну шкалу со средним 0, перед применением PCA
Загрузим данные биологического анализа пациентов с раком и без него.
В данном случае наши данные уже предварительно обработаны, поэтому стандартизацию проводить не будем
# 1. First we import the pandas Python package.
# 2. Then we read in the file that contains the RNA-seq data.
# The RNA-seq data is stored in a tab-delimited file (.tab extension),
# which is why we use the read_table pandas method.
# The read_table method is named this way because
# it reads tab-delimited data by default.
# We want to tell the read_table method that the data is tab delimited,
# that is why we supply the '\t' argument.
# 3. We want to tell the read_table method that the first column
# contains our sample IDs, which is the column with index 0.
# We do this by telling it to use the index_col argument and
# setting that equal to 0.
# 4. We don't actually need the header information in this specific file,
# so we don't have to tell pandas to parse the header information.
# 5. We assign the RNA-seq data to an object named rnadata
rnadataset = pd.read_table(
"https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/rnaseq_data.tab.txt",
index_col=0,
header=None,
)
print("dataset shape: ", rnadataset.shape)
dataset shape: (358, 71586)
rnadataset.columns = list(rnadataset.columns[:-2]) + ["dataset", "sample type"]
rnadataset.head()
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... | 71577 | 71578 | 71579 | 71580 | 71581 | 71582 | 71583 | 71584 | dataset | sample type | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | |||||||||||||||||||||
| GSM1296956 | 13.374975 | 3.536581 | 13.644486 | 3.929925 | 5.485977 | 9.363128 | 13.134106 | 4.318162 | 10.050190 | 10.605277 | ... | 11.111910 | 6.889096 | 10.636753 | 6.656603 | 11.054070 | 6.914937 | 8.949687 | 8.982860 | GSE53622 | cancer |
| GSM1296957 | 13.555346 | 4.772572 | 14.153843 | 4.388201 | 5.412374 | 9.339831 | 13.789576 | 4.211175 | 11.242888 | 10.518348 | ... | 10.998240 | 8.220715 | 10.645032 | 5.799432 | 10.951782 | 5.358962 | 8.951818 | 8.147058 | GSE53622 | normal |
| GSM1296958 | 13.396705 | 4.804828 | 13.948490 | 4.395992 | 5.627752 | 7.867446 | 13.424588 | 4.097212 | 10.568927 | 10.666406 | ... | 10.498048 | 8.145627 | 11.452488 | 6.164146 | 11.492929 | 6.189310 | 9.091511 | 10.021106 | GSE53622 | cancer |
| GSM1296959 | 13.843843 | 4.563550 | 14.390648 | 4.697154 | 5.511075 | 8.943584 | 14.181927 | 4.766994 | 10.418466 | 10.924152 | ... | 10.680012 | 8.450327 | 10.966135 | 6.482977 | 10.869259 | 6.683605 | 9.321499 | 9.278717 | GSE53622 | normal |
| GSM1296960 | 13.505687 | 4.750858 | 14.049400 | 4.476174 | 5.753380 | 8.475744 | 14.255647 | 4.344796 | 10.189663 | 10.651861 | ... | 9.778142 | 7.615217 | 10.570247 | 5.861632 | 11.168351 | 6.343246 | 8.793520 | 11.562505 | GSE53622 | cancer |
5 rows × 71586 columns
# We remove the dataset and sample type columns from the data frame and
# store the data frame in X
x = rnadataset.drop(labels=["dataset", "sample type"], axis=1)
# We store the dataset and sample type columns in the labels data frame
labels = rnadataset.loc[:, ["dataset", "sample type"]]
# Finding the top two principal components of the data
pca_decomposer = PCA(n_components=2)
pca_decomposer.fit(x)
PCA(n_components=2)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
PCA(n_components=2)
# Run PCA on the features
x_reduced = pca_decomposer.transform(x)
# Display a scatterplot of the transformed dataset
plt.figure(figsize=(8, 6))
plt.title("PCA plot", size=24)
plt.xlabel("PC1", size=16)
plt.ylabel("PC2", size=16)
sns.scatterplot(x=x_reduced[:, 0], y=x_reduced[:, 1], hue=labels["sample type"]);
Даже не понимая, что за признаки у нас в колонках, мы видим несколько интересных вещей.
Во-первых, синяя точка на оранжевой территории и оранжевая на синей — видимо, выбросы.
Кроме этого мы видим, что почему-то у нас есть 4 почти равноудаленных кластера, по два на рак и нормальную ткань
# Run PCA on the features
x_reduced = pca_decomposer.transform(x)
# Display a scatterplot of the transformed dataset
plt.figure(figsize=(8, 6))
plt.title("PCA plot", size=24)
plt.xlabel("PC1", size=16)
plt.ylabel("PC2", size=16)
sns.scatterplot(
x=x_reduced[:, 0],
y=x_reduced[:, 1],
hue=labels["sample type"],
style=labels["dataset"],
);
Видим, что в пределах данных одного эксперимента рак и опухоль разделяются хорошо. Но при этом данные между разными экспериментами отличаются так же, как и рак от опухоли.
Этот эффект называется батч-эффектом и говорит о том, что нужно нормализовывать данные в пределах эксперимента каким-то хитрым образом, чтобы научить модель на новых данных отличать рак от нормальной ткани.
Таким образом, с помощью PCA мы нашли выбросы и артефакт в данных.
Рассмотрим, как PCA применялся для решения практической задачи распознавания лиц*.
Датасет: Labeled Faces in the Wild
* Сейчас для этого используются более эффективные алгоритмы, использующие CNN.
Загрузим датасет и распакуем его на диск VM Colab
# http://conradsanderson.id.au/lfwcrop/ (LFWcrop Face Dataset, greyscale version)
# 1. Downloading the LFWcrop dataset from the website.
# 2. Unzipping the dataset from the downloaded file.
# 3. Opening the directory with the faces.
dir = "lfwcrop_grey/faces"
# http://conradsanderson.id.au/lfwcrop/ (LFWcrop Face Dataset, greyscale version)
!wget -q https://edunet.kea.su/repo/EduNet-web_dependencies/datasets/lfwcrop_grey.zip
!unzip -q lfwcrop_grey.zip
import os
plt.rcParams["axes.grid"] = False
def show_faces(imgs, titles, h=64, w=64):
plt.figure(figsize=(16, 4))
for i in range(min(imgs.shape[0], 5)):
plt.subplot(1, 5, i + 1)
plt.imshow(imgs[i].reshape((h, w)), cmap=plt.cm.gray)
plt.title(titles[i])
# Get first 1000 files
celebrity_photos = os.listdir(dir)[1:1001]
celebrity_imgs = [dir + "/" + photo for photo in celebrity_photos]
# Load images from disk
imgs = np.array([plt.imread(img) for img in celebrity_imgs], dtype=np.float64)
# Extract real celebrity name from file name
celebrity_names = [
name[: name.find("0") - 1].replace("_", " ") for name in celebrity_photos
]
print(imgs[0].shape)
show_faces(imgs, celebrity_names)
(64, 64)
Предобработка данных: Преобразуем изображения в вектора и центрируем их
# Stretch to vector
x = imgs.reshape(imgs.shape[0], 64 * 64)
print(x.shape)
mean = np.mean(x, axis=0)
# Center: substract mean
centered_faces = x - mean
plt.imshow(mean.reshape(64, 64), cmap=plt.cm.gray)
plt.show()
(1000, 4096)
Найдем собственные вектора. Аналогия с фотороботом.
# https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html
# n_components == min(n_samples, n_features)
# 1. Load the faces data.
# 2. Apply PCA.
# 3. Extract the principal components.
# 4. Reshape the principal components so that they have the right shape.
# 5. Display the reshaped principal components.
pca_faces = sklearn.decomposition.PCA() # 1000x4096
pca_faces.fit(centered_faces)
eigenfaces = pca_faces.components_
reshaped_eigenfaces = eigenfaces.reshape((1000, 64, 64))
eigenface_titles = ["eigenface %d" % i for i in range(reshaped_eigenfaces.shape[0])]
show_faces(reshaped_eigenfaces, eigenface_titles)
Восстановим лица с использованием n < 4096 компонент
def create_embedding(img, n_components):
# Generate embedding for first image using only 10 first components
img = img.reshape(64 * 64) - mean
emb = np.dot(img, eigenfaces[:n_components].T) # (1,4096) * (4096,1)
# print(emb,emb.shape) # 10 - 500 numbers only!
# Recover image from embedding
recovered_img = np.dot(emb, eigenfaces[:n_components])
recovered_img += mean # shift by mean
return emb, recovered_img
# Show images recovered from embeddings of various sizes
original_img = imgs[0]
titles = []
img_list = []
for n in [10, 25, 100, 500]:
embedding, recovered = create_embedding(original_img, n)
img_list.append(recovered)
titles.append(f"Components {n}")
img_list.append(original_img)
titles.append("Original")
show_faces(np.array(img_list, dtype=object), titles)
В данном случае требование на ортогональность компонент, выделяемых PCA, фактически мешает нам
Рассмотрим случай выборки, которая сгенерирована из двух вытянутых нормальных распределений, чьи основные оси неортогональны друг другу:

В примере ниже дисперсии не отражают интересующих нас направлений в данных:

Очевидно, что в данном случае метод главных компонент будет считать вертикальную компоненту более значимой для описания набора данных, чем горизонтальную.
Но, например, в случае, когда данные из левого и правого кластера относятся к разным классам, для их линейной разделимости вертикальная компонента является шумовой. Несмотря на это, её метод главных компонент никогда шумовой не признает, и есть вероятность, что отбор признаков с его помощью выкинет из ваших данных значимые для решаемой вами задачи компоненты просто потому, что вдоль них значения имеют низкую дисперсию.
Справляться с такими ситуациями могут некоторые другие методы уменьшения размерности данных, например, метод независимых компонент (Independent Component Analysis, ICA).
Как мы увидели в предыдущих примерах, обычный PCA далеко не всегда работает хорошо. В частности, могут быть ситуации, когда построенная PCA проекция не дает хорошего разбиения объектов на группы. Для набора картинок с написанными от руки цифрами MNIST, PCA даст такой результат:

Также бывают ситуации, когда оптимально спроецировать не на некоторую плоскость, а на многообразие (кривая плоскость), как показано на картинке ниже.

В данном случае оптимально спроецировать на S-образную кривую.
В связи с вышеописанными случаями, ниже мы рассмотрим более сильные методы.
Как уже упоминалось, иногда невозможно захватить всю информацию линейной проекцией, хотя кривая поверхность с такой же размерностью это позволяет сделать. Одним из подходов к решению данной проблемы является задача перевода признаков в нелинейное пространство.
Kernel Trick избегает явного перевода наших признаков в пространство новых признаков, ведь пространства бывают очень большие, а нам бы хотелось сэкономить память компьютера. Оказывается, для PCA не важны собственно признаки объектов, а важны скалярные произведения между объектами.
И это скалярное произведением позволяет подсчитывать напрямую функция $k(\mathbf {x} ,\mathbf {x'})$, которую часто называют ядром или ядерной функцией (kernel, kernel function)
Бывают разные ядра, которые считают скалярное произведение в разных пространствах
# https://scikit-learn.org/stable/auto_examples/decomposition/plot_kernel_pca.html
from sklearn.datasets import make_circles
np.random.seed(42)
# 1. Make_circles creates a data set of 400 points that form concentric circles with a gap of 50 points.
# 2. The factor parameter controls the size of the inner circles.
# 3. The noise parameter controls the amount of noise added to the data.
# 4. The result is a 360-feature dataset of concentric circles with gaps.
x, y = make_circles(n_samples=400, factor=0.3, noise=0.05, random_state=42)
Возьмем две концентрические окружности
plt.figure(figsize=(5, 5))
plt.title("Original space")
reds = y == 0
blues = y == 1
plt.scatter(x[reds, 0], x[reds, 1], c="red", s=20, edgecolor="k")
plt.scatter(x[blues, 0], x[blues, 1], c="blue", s=20, edgecolor="k")
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.show()
Обычный PCA не может их разделить
pca = PCA()
x_pca = pca.fit_transform(x)
plt.figure(figsize=(5, 5))
plt.scatter(x_pca[reds, 0], x_pca[reds, 1], c="red", s=20, edgecolor="k")
plt.scatter(x_pca[blues, 0], x_pca[blues, 1], c="blue", s=20, edgecolor="k")
plt.title("Projection by PCA")
plt.xlabel("1st principal component")
plt.ylabel("2nd component")
plt.show()
А вот KernelPCA справляется
from sklearn.decomposition import KernelPCA
# 1. Create a PCA object to perform the PCA transformation
# using the RBF kernel (specified using kernel="rbf").
# Setting fit_inverse_transform=True. This will make the object use the
# transformed data from the first step when transforming new, unseen data points.
# 2. Let the PCA object fit and transform the data,
# then get the transformed data back.
kpca = KernelPCA(kernel="rbf", fit_inverse_transform=True, gamma=10)
x_kpca = kpca.fit_transform(x)
plt.figure(figsize=(5, 5))
plt.scatter(x_kpca[reds, 0], x_kpca[reds, 1], c="red", s=20, edgecolor="k")
plt.scatter(x_kpca[blues, 0], x_kpca[blues, 1], c="blue", s=20, edgecolor="k")
plt.title("Projection by KPCA")
plt.xlabel(r"1st principal component in space induced by $\phi$")
plt.ylabel("2nd component")
plt.show()
Хотя, конечно, и восстанавливать он будет не идеально: работал-то он по факту в пространстве бОльшей размерности и оси строил там.
# 1. The 'kpca' variable is a KernelPCA object that is initialized with 'n_components' set to 2.
# 2. Then it applies the kernel function specified in the 'kernel' variable and then transforms the data based on the kernel, and gets the transformed data.
# 3. Then it returns the transformed data.
# 4. Then we get the inverse transformation by simply calling "kpca.inverse_transform(x_kpca)"
# 5. Finally, we plot the transformed data.
x_back = kpca.inverse_transform(x_kpca)
plt.figure(figsize=(5, 5))
plt.scatter(x_back[reds, 0], x_back[reds, 1], c="red", s=20, edgecolor="k")
plt.scatter(x_back[blues, 0], x_back[blues, 1], c="blue", s=20, edgecolor="k")
plt.title("Original space after inverse transform")
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.tight_layout()
plt.show()
Kernel PCA довольно чувствителен к выбору ядра.
К примеру, для данных, расположенных на трех окружностях:

в зависимости от выбора ядра мы будем получать совершенно разные отображение в спрямляющее пространство:

Существуют и другие методы понижения размерности в данных. К примеру, t-SNE и UMAP.
Они решают немного иначе поставленную задачу: из измерения новой размерности мы не должны легко переходить в старое измерение. Взамен этого требуется, чтобы сохранялись расстояния между объектами. Причем, особое внимание уделяется близким расстояниям. Далекие же могут не сохраняться.
Идея состоит в том, чтобы не напрямую максимизировать дисперсию, а найти такое пространство, в котором расстояние между объектами будет сохраняться или по крайне мере не сильно меняться.
При этом будем больше беспокоиться о расстоянии между близкими объектами, нежели о расстоянии между далекими.
Для простоты будем в качестве исходного пространства рассматривать 2-мерное


Далее эти ненормированные расстояния нормируем на их сумму, чтобы для каждой точки похожести несли примерно одинаковый смысл. В итоге получается такая формула: $$\large p_{j\mid i}={\frac {\exp(-\lVert \mathbf{x}_{i}-\mathbf {x}_{j}\rVert^{2}/2\sigma_{i}^{2})}{\sum_{k\neq i}\exp(-\lVert \mathbf{x}_{i}-\mathbf{x}_{k}\rVert^{2}/2\sigma_{i}^{2})}}$$
Стандартное отклонение будет различным для каждой точки. Оно подбирается бинарным поиском так, чтобы точки в областях с большей плотностью имели меньшую дисперсию. Для этого используется параметр perplexity: чем он больше, тем более далеким соседям уделяется внимание (стандартные отклонения становятся в целом больше).
Чтобы получить симметричные расстояния $p_{ij}$, их считают по следующей формуле:
$$p_{ij} = \frac{p_{j\mid i} + p_{i\mid j}}{2N}$$В итоге получаем матрицу расстояний следующего вида:

Обычно в случае t-SNE используют пространства двумерные и трехмерные. Это вызвано во многом скоростью работы метода и тем, что он преимущественно используется для визуализации.
Для простоты будем в качестве пространства низкой размерности рассматривать одномерное.
Расположим точки, соответствующие точкам из исходного пространства, случайным образом в одномерном пространстве.

Точно так же будем считать расстояние между выбранной точкой и остальными и использовать эти расстояния не в качестве $x$, а в качестве $y$, и, как следствие, similarity, будем использовать не нормальное распределение, а распределение Стьюдента.

Почему? Оно более "тяжелое" в хвостах и поэтому дает возможность больше внимания уделять далеким точкам. Это позволяет компенсировать дисбаланс в распределении расстояний в пространстве большей и меньшей размерностей. Без этого точки у нас будут "липнуть" друг к другу.
В итоге мы получили две матрицы расстояний: в исходном и в новом пространстве:

Они абсолютно друг на друга не похожи, что логично: пока что наша проекция в новое пространство абсолютно случайная. Надо как-то править представление в новом пространстве. Именно для этого авторы и использовали плотности и прочее — чтобы задать теперь хорошую cost-функцию, которую затем нужно минимизировать.
Cost-функцией будет $$Cost = KL(P||Q) = \sum_{i \neq j}{p_{ij} log \frac{p_{ij}}{q_{ij}}}$$
Минимизируем это градиентным спуском.
Фактически, такое требование минимизировать cost-функцию говорит следующее: я хочу получить такое представление, чтобы объекты, которые находились в исходном пространстве близко, вероятно, находились и в представлении близко, а объекты, которые находились далеко — далеко.
Для того, чтобы t-SNE сходился лучше и определеннее, в качестве изначальных координат точек в новом пространстве можно использовать не случайный шум, а первые две компоненты PCA.
Преследуем две цели: уменьшить время работы t-SNE (который работает очень медленно) и убрать эффект шума на t-SNE — он может на него реагировать, особенно при условии, что схождения к минимуму мы можем не дождаться.
import sklearn.manifold
# 1. Firstly we reduce the dimensionality of the data to 6 features using PCA.
# 2. Then we take the first two PCA components and use this
# as an initial approximation for the T-SNE algorithm.
# 3. Then we fit T-SNE on the data and plot the first two dimensions
# of the T-SNE output, which are represented in green.
# 4. The visualization makes clear that there are distinct clusters in our data
x_reduced = PCA(n_components=6).fit_transform(x_scRNAseq)
model = sklearn.manifold.TSNE(
n_components=2,
init=x_reduced[:, 0:2], # often use as a reasonable approximation
perplexity=40, # important parameter
verbose=2,
learning_rate="auto",
)
manifold = model.fit_transform(x_reduced)
plt.figure(figsize=(10, 5))
plt.scatter(manifold[:, 0], manifold[:, 1], c=y_scRNAseq, cmap="tab20", s=20)
plt.title("TSNE: scRNAseq", fontsize=25)
plt.xlabel("TSNE1", fontsize=22)
plt.ylabel("TSNE2", fontsize=22)
plt.show()
[t-SNE] Computing 121 nearest neighbors... [t-SNE] Indexed 8617 samples in 0.012s... [t-SNE] Computed neighbors for 8617 samples in 0.543s... [t-SNE] Computed conditional probabilities for sample 1000 / 8617 [t-SNE] Computed conditional probabilities for sample 2000 / 8617 [t-SNE] Computed conditional probabilities for sample 3000 / 8617 [t-SNE] Computed conditional probabilities for sample 4000 / 8617 [t-SNE] Computed conditional probabilities for sample 5000 / 8617 [t-SNE] Computed conditional probabilities for sample 6000 / 8617 [t-SNE] Computed conditional probabilities for sample 7000 / 8617 [t-SNE] Computed conditional probabilities for sample 8000 / 8617 [t-SNE] Computed conditional probabilities for sample 8617 / 8617 [t-SNE] Mean sigma: 0.336887 [t-SNE] Computed conditional probabilities in 0.326s [t-SNE] Iteration 50: error = 72.8291931, gradient norm = 0.0087157 (50 iterations in 6.128s) [t-SNE] Iteration 100: error = 72.3467102, gradient norm = 0.0023780 (50 iterations in 4.831s) [t-SNE] Iteration 150: error = 72.2015839, gradient norm = 0.0015488 (50 iterations in 4.784s) [t-SNE] Iteration 200: error = 72.0850143, gradient norm = 0.0012886 (50 iterations in 5.579s) [t-SNE] Iteration 250: error = 71.9976196, gradient norm = 0.0010311 (50 iterations in 4.534s) [t-SNE] KL divergence after 250 iterations with early exaggeration: 71.997620 [t-SNE] Iteration 300: error = 2.2893496, gradient norm = 0.0108292 (50 iterations in 5.201s) [t-SNE] Iteration 350: error = 1.9024110, gradient norm = 0.0103034 (50 iterations in 3.778s) [t-SNE] Iteration 400: error = 1.7143979, gradient norm = 0.0090468 (50 iterations in 3.329s) [t-SNE] Iteration 450: error = 1.6102605, gradient norm = 0.0081399 (50 iterations in 3.981s) [t-SNE] Iteration 500: error = 1.5437438, gradient norm = 0.0075030 (50 iterations in 2.984s) [t-SNE] Iteration 550: error = 1.4965279, gradient norm = 0.0069944 (50 iterations in 2.938s) [t-SNE] Iteration 600: error = 1.4613835, gradient norm = 0.0066300 (50 iterations in 3.909s) [t-SNE] Iteration 650: error = 1.4336526, gradient norm = 0.0063218 (50 iterations in 2.845s) [t-SNE] Iteration 700: error = 1.4119039, gradient norm = 0.0059573 (50 iterations in 2.865s) [t-SNE] Iteration 750: error = 1.3946626, gradient norm = 0.0054747 (50 iterations in 2.852s) [t-SNE] Iteration 800: error = 1.3813536, gradient norm = 0.0047092 (50 iterations in 3.823s) [t-SNE] Iteration 850: error = 1.3716450, gradient norm = 0.0039969 (50 iterations in 2.870s) [t-SNE] Iteration 900: error = 1.3644423, gradient norm = 0.0033520 (50 iterations in 2.836s) [t-SNE] Iteration 950: error = 1.3591452, gradient norm = 0.0027038 (50 iterations in 2.801s) [t-SNE] Iteration 1000: error = 1.3549483, gradient norm = 0.0023919 (50 iterations in 3.640s) [t-SNE] KL divergence after 1000 iterations: 1.354948
И покрасим по разметке, которая нам известна из эксперимента. Видим, что разделение очень хорошее
Определяет то, как подбирается стандартное отклонение для распределения расстояний для каждой точки. Чем больше perplexity, тем более глобально мы смотрим на структуру.
Как считаются расстояния между точками — metric. По умолчанию используется евклидово расстояние, но часто помогают и другие (например, косинусное).
Шаг градиентного спуска, тоже влияет на полученное представление.
Чтобы продемонстрировать проблемы t-SNE, берем оригинальные данные в 2D пространстве и добавляем к ним новые признаки, взятые из нормального шума. Далее пытаемся восстановить изначальную структуру.
Низкоразмерное представление, которое вы получите, будет отличаться между запусками, если не зафиксировать random seed. Может отличаться довольно сильно.
Если у вас появились новые данные, то добавить их на представление, полученное при помощи t-SNE ранее — нетривиальная задача. Для разных областей есть свои "подгоны", но все это эвристика.




Из-за указанных недостатков результат t-SNE НЕЛЬЗЯ использовать для кластеризации.
UMAP — uniform manifold approximation and projection. Видео
Использует похожую на t-SNE идею, но иначе, в результате чего получает много выгодных бонусов.
Внутри себя метод строит граф, в котором ребрами соединены между собой k ближайших соседей. При этом эти ребра неравноправны: если для данной пары точек расстояние между ними сильно больше, чем расстояния между ними и другими точками, то и ребро будет иметь маленький вес.

Далее задача состоит в том, чтобы в пространстве более низкой размерности получился граф, похожий на тот, который был в пространстве высокой размерности. Для этого оптимизируем низкоразмерное представление градиентным спуском.
from IPython.display import clear_output
!pip install -q umap-learn
!pip install -q --upgrade tbb
clear_output()
from umap import UMAP
# Converts the original expression matrix (scRNAseq) into a 9-dimensional PCA space
x_reduced = PCA(n_components=9).fit_transform(x_scRNAseq)
# Initializes UMAP with the PCA components
model = UMAP(
n_components=2,
min_dist=1,
n_neighbors=93,
init=x_reduced[:, 0:2],
# it is recommended to use the first two components of PCA for initialization of UMAP and t-SNE
n_epochs=1000,
verbose=2,
)
# Runs the UMAP algorithm on the PCA transformed data
umap = model.fit_transform(x_reduced)
clear_output()
# Plots the results of the UMAP transformation
plt.figure(figsize=(10, 5))
plt.scatter(umap[:, 0], umap[:, 1], c=y_scRNAseq, cmap="tab20", s=20)
plt.title("UMAP: scRNAseq", fontsize=25)
plt.xlabel("UMAP1", fontsize=22)
plt.ylabel("UMAP2", fontsize=22)
plt.show()
Число соседей, которые ищутся для каждой точки. Влияет на то, насколько глобально мы смотрим на структуру данных.
Влияет на то, насколько близко могут находиться между собой точки в новом представлении.
Определяет, как считаются расстояния между точками. По умолчанию Евклидово расстояние, но это не всегда дает лучший результат.
Выдает результаты, похожие на t-SNE, но работает в разы быстрее
UMAP может проецировать точки из новых датасетов на уже имеющееся представление.
Если у вас есть признаки, сильно отличающиеся по своим свойствам, то можно построить для них представления отдельно с разными метриками, а далее объединить их.
Параметры n_neighbours и min_dist намного понятнее их аналога — perplexity.
Кроме того, его можно использовать для понижения размерности не только до 2-3 (в целях визуализации), но и для больших размерностей, с которыми потом работать другими методами (хотя здесь надо быть аккуратным, он тоже склонен деформировать дальние расстояния)
Плохая идея — интерпретировать расстояния между кластерами и их размеры для 2D представлений.
Но в случае UMAP это менее выражено.

Если же отображать в пространство размерности большей, чем два, то можно получить и очень хорошие представления. Но это все эвристика, может и не повезти.
UMAP позволяет передать в него метки объектов — вы можете получать представление, которое оптимизировано под имеющуюся у вас информацию о кластерах.
UMAP позволяет передать в него метки только для части объектов — вы можете получать представление, которое оптимизировано под имеющуюся у вас информацию о кластерах, но при этом не оставляет без внимания объекты без меток.
Когда говорят про задачу кластеризации подразумевают примерно следующее:
У нас есть данные, и мы хотим поделить эти данные по каким-то группам, где в каждой группе будут объекты, похожие друг на друга. Под похожестью как правило понимается выбранная метрика расстояния.

Основные цели кластеризации:
Исследование данных. Мы хотим понять, какие кластеры являются ярко выраженными, и сделать дополнительные выводы о наших данных.
Нахождение аномалий/выбросов. Мы можем искать объекты, которые сильно отличаются от всех остальных и не принадлежат никакому кластеру.
Создание дополнительных признаков. Кластер для объекта уже является дополнительным категориальным признаком.
Непосредственно классификация. Например, можем считать получившиеся кластеры классами и классифицировать объекты таким образом.
Алгоритмов кластеризации существует большое количество, и все работают по-разному, имеют разные параметры для настройки. Мы рассмотрим два наиболее популярных: K-Means и DBSCAN.


Особенности K-Means:

DBSCAN (Density-based spatial clustering of applications with noise, плотностной алгоритм пространственной кластеризации с присутствием шума), как следует из названия, оперирует плотностью данных. На вход требуется матрица близости и два загадочных параметра — радиус $\varepsilon$-окрестности и количество соседей.
Алгоритм выглядит следующим образом:
Иначе:
Методы понижения размерности, такие как UMAP и t-SNE, могут быть использованы как эффективный метод предобработки данных для последующей передачи в алгоритмы кластеризации на основе плотности. Данные методы понижения размерности не полностью сохраняют информацию о плотности распределения объектов при осуществлении проекции в низкоразмерное пространство, поэтому следует относиться к такой предобработке с некоторой осторожностью (рекомендуем ознакомиться с вот этим обсуждением на stackexchange). Несмотря на эти опасения, все же есть веские причины для использования данных методов понижения размерности в качестве этапа предварительной обработки для кластеризации. Как и при любом подходе к кластеризации, необходимо провести исследование и оценку полученных кластеров, чтобы попытаться валидировать разбиение на них, если это возможно.
Загрузим датасет с одноканальными $8 \times 8$ изображениями рукописных цифр:
from sklearn import datasets
digits = datasets.load_digits(n_class=10)
x = digits.data
y = digits.target
n_samples, n_features = x.shape
print(x.shape)
(1797, 64)
Понизим размерность данных $64 \rightarrow 2$ при помощи t-SNE:
from sklearn import manifold
# t-SNE embedding of the digits dataset
tsne = manifold.TSNE(n_components=2, init="pca", random_state=42, learning_rate="auto")
x_tsne = tsne.fit_transform(x)
Понизим размерность данных $64 \rightarrow 2$ при помощи UMAP:
umap = UMAP(n_neighbors=5)
x_umap = umap.fit_transform(x)
Визуализируем результаты:
from matplotlib import offsetbox
def plot_embedding(x, title=None):
x_min, x_max = np.min(x, 0), np.max(x, 0)
x = (x - x_min) / (x_max - x_min) # normalization of x to (0..1) range
plt.figure()
ax = plt.subplot(111)
for i in range(x.shape[0]):
plt.text(
x[i, 0],
x[i, 1],
str(y[i]),
color=plt.cm.Set1(y[i] / 10.0),
fontdict={"weight": "bold", "size": 9},
)
if hasattr(offsetbox, "AnnotationBbox"):
# only print thumbnails with matplotlib > 1.0
shown_imgs = np.array([[1.0, 1.0]]) # just something big
for i in range(x.shape[0]):
dist = np.sum((x[i] - shown_imgs) ** 2, 1)
if np.min(dist) < 4e-3:
# don't show points that are too close
continue
shown_imgs = np.r_[shown_imgs, [x[i]]]
img_box = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r), x[i]
)
ax.add_artist(img_box)
plt.xticks([]), plt.yticks([])
if title is not None:
plt.title(title)
plt.figure()
ax = plt.subplot(111)
for i in range(x.shape[0]):
plt.text(
x[i, 0],
x[i, 1],
str(y[i]),
color=plt.cm.Set1(y[i] / 10.0),
fontdict={"weight": "bold", "size": 9},
)
plt.xticks([]), plt.yticks([])
if title is not None:
plt.title(title)
# t-SNE embedding of the digits dataset
plot_embedding(x_tsne, "t-SNE embedding of the digits")
# UMAP embedding of the digits
plot_embedding(x_umap, "UMAP embedding of the digits")
Как нетрудно заметить, при использовании UMAP точки из датасета при проекции в низкоразмерное пространство оказались расположены более "кучно", нежели чем при использовании t-SNE.
Теперь попробуем кластеризовать наши данные при помощи K-Means. Для оценки качества воспользуемся стандартными метриками adjusted_rand_score и adjusted_mutual_info_score из sklearn.metrics.
import sklearn.cluster as cluster
kmeans_labels_on_raw = cluster.KMeans(n_clusters=10, n_init="auto").fit_predict(x)
from sklearn.metrics import adjusted_rand_score, adjusted_mutual_info_score
def plot_clustering_metrics(true_l, pled_l, title):
ari = adjusted_rand_score(true_l, pled_l)
ami = adjusted_mutual_info_score(true_l, pled_l)
fig, ax = plt.subplots(1, 1, figsize=(10, 6))
plt.title(f"Clustering metrics for {title}\n\n 1.0 is best")
width = 0.75
ind = np.arange(2)
ax.barh(ind, [ari, ami], width)
ax.grid(axis="x")
ax.set_xlim([0, 1.0])
for i, v in enumerate([ari, ami]):
ax.text(v + 0.01, i, f"{v:1.2f}", color="black")
ax.set_yticks(ind)
ax.set_yticklabels(["ARI", "AMI"], minor=False)
plt.show()
plot_clustering_metrics(y, kmeans_labels_on_raw, "kNN on raw dataset")
Теперь передадим K-Means данные после понижения размерности:
kmeans_labels_on_x_tsne = cluster.KMeans(n_clusters=10, n_init="auto").fit_predict(
x_tsne
)
kmeans_labels_on_x_umap = cluster.KMeans(n_clusters=10, n_init="auto").fit_predict(
x_umap
)
plot_clustering_metrics(y, kmeans_labels_on_x_tsne, "kNN on t-SNE data")
plot_clustering_metrics(y, kmeans_labels_on_x_umap, "kNN on UMAP data")
Применяя методы понижения размерности на этапе предобработки данных, мы смогли значительно улучшить качество кластеризации. Использование UMAP в разобранном нами примере позволило достичь лучших результатов по сравнению с t-SNE и получить прирост практически в 20% относительно метрик качества кластеризации.